箱梁梁格法建模若干问题的探讨

田 亮 高 伟

(北京交通运输职业学院，北京 101121)

1 概述

随着宽桥、斜桥、弯桥、不规则支撑等复杂结构在桥梁工程中的广泛应用，传统的单梁计算模型已无法满足工程实际的需要，梁格法被认为是一种较为实用的分析方法。但在梁格法应用中，纵向梁格划分方式、横梁模拟方法及梁格单元尺寸等方面尚存在不同的意见，其对计算精度的影响值得进一步分析研究。本文以某两跨连续箱梁桥为例，通过分析纵向梁格划分方式、横梁模拟方法及梁格单元尺寸对计算结果的影响，确定合理的建模方法。

2 计算模型的建立

2.1 背景工程

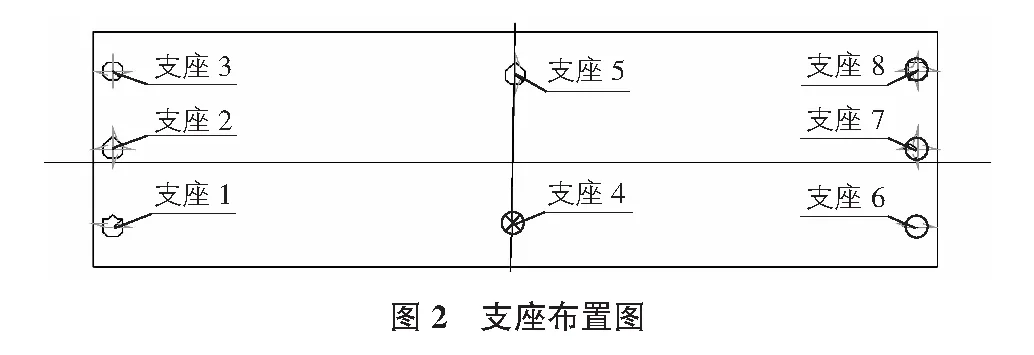
背景工程为2×30 m预应力混凝土连续箱梁。单箱双室截面，梁高1.7 m，梁宽17.5 m。截面尺寸和支座布置形式见图1，图2。

2.2 梁格划分方式

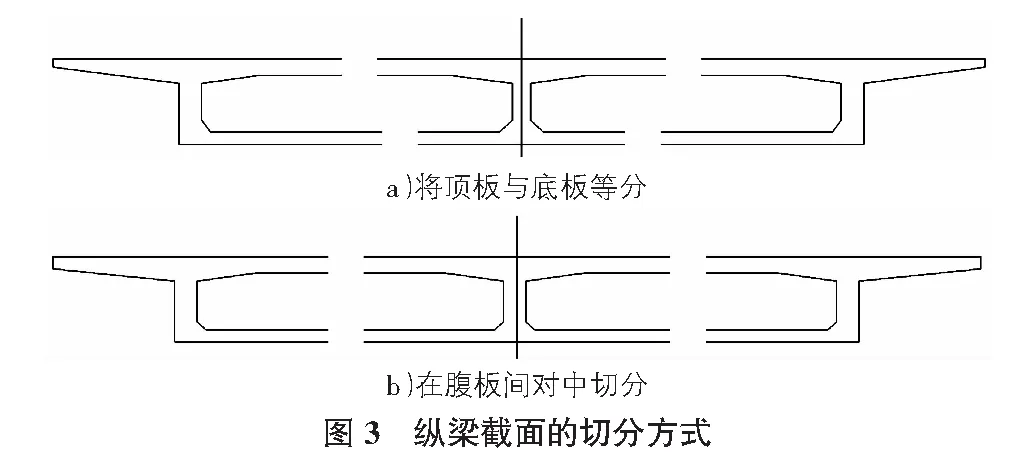
纵向梁格划分方式：方式一：采用顶板和底板等分(见图3a))，使纵向梁格的中性轴与整体上部结构的主轴基本重合[1]，梁格截面绕相同的水平面转动，避免由于纵向相对位移产生的剪力。方式二:采用腹板间对中切分(见图3b))。

横向梁格的截面形式：方式一：腹板很薄的工字形截面[2]，方式二：采用矩形截面。两种截面形式见图4，其中d1,d2分别为箱梁顶板与底板厚，δ为一很小值。

荷载工况：工况一，自重作用。工况二，自重+预应力作用。工况三，自重+预应力作用+左腹板处施加20 kN/m偏心荷载。通过三种不同的荷载工况作用。

有限元模型：考虑不同梁格划分方式模型；单梁模型；ansys Solid65单元模型。

3 纵向梁格划分方式的影响

3.1 各荷载工况作用下的支座反力

各荷载工况作用下，不同模型桥梁支座反力的计算结果如图5所示。

以ansys模型计算结果为标准，比较不同荷载工况下，几种建模方式与ansys计算结果的比对，见表1～表3(小于ansys计算结果为负值)。

表1 荷载工况一作用下支座反力与ansys计算结果差值 %

表2 荷载工况二作用下支座反力与ansys计算结果差值 %

表3 荷载工况三作用下支座反力与ansys计算结果差值 %

由表1～表3可见：荷载工况一最大计算差值，建模方式一为8.2%，建模方式二为4.7%，单梁模型为25.4%；荷载工况二最大计算差值，建模方式一为9.4%，建模方式二为37.5%，单梁模型为23.7%；荷载工况三最大计算差值，建模方式一为8.7%，建模方式二为33.2%，单梁模型为26.8%。其中，建模方式一支座反力的计算结果差值最小。

3.2 各荷载工况作用下桥梁跨中竖向变形

各荷载工况作用下，不同模型桥梁跨中竖向变形的计算结果如图6所示。

由图6竖向变形曲线可以看出：在工况一作用下，三种建模方式计算结果很接近，但差值偏大；工况二跨中竖向位移差值，建模方式一为3.0%，建模方式二为8.0%，单梁模型为8.3%；在荷载工况三作用下，右侧腹板跨中竖向位移差值：建模方式一为3.8%，建模方式二为7.0%，单梁模型为6.4%，左侧腹板跨中竖向位移差值：建模方式一为1.3%，建模方式二为13.3%，单梁模型为27.4%。其中，荷载工况一作用下三种建模方式的差值均较大。荷载工况二、三作用下，建模方式一的差值最小。

4 横向梁格截面形式

4.1 各荷载工况作用下桥梁的支座反力

各荷载工况作用下，不同模型桥梁支座反力的计算结果如图7所示。

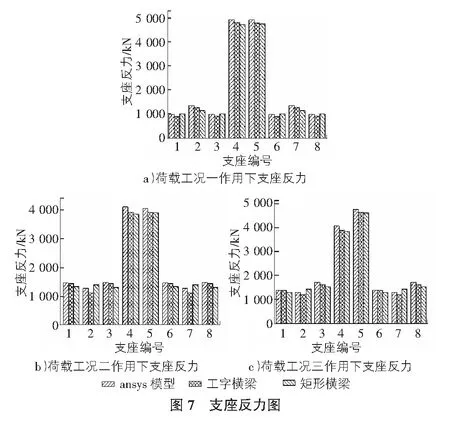
比较不同荷载工况下，两种横梁截面形式与ansys计算结果的差值，见表4～表6(小于ansys计算结果为负值)。

由表4～表6可知：荷载工况一最大计算差值，工字横梁模型为8.2%，矩形横梁模型为16.2%；荷载工况二最大计算差值，工字横梁模型为9.4%，矩形横梁模型为11.0%；荷载工况三最大计算差值，工字横梁模型为8.7%，矩形横梁模型为11.6%。其中，工字横梁模型支座反力计算误差最小。

表4 荷载工况一作用下支座反力与ansys计算结果差值 %

表5 荷载工况二作用下支座反力与ansys计算结果差值 %

表6 荷载工况三作用下支座反力与ansys计算结果差值 %

4.2 各荷载工况作用下桥梁的竖向变形

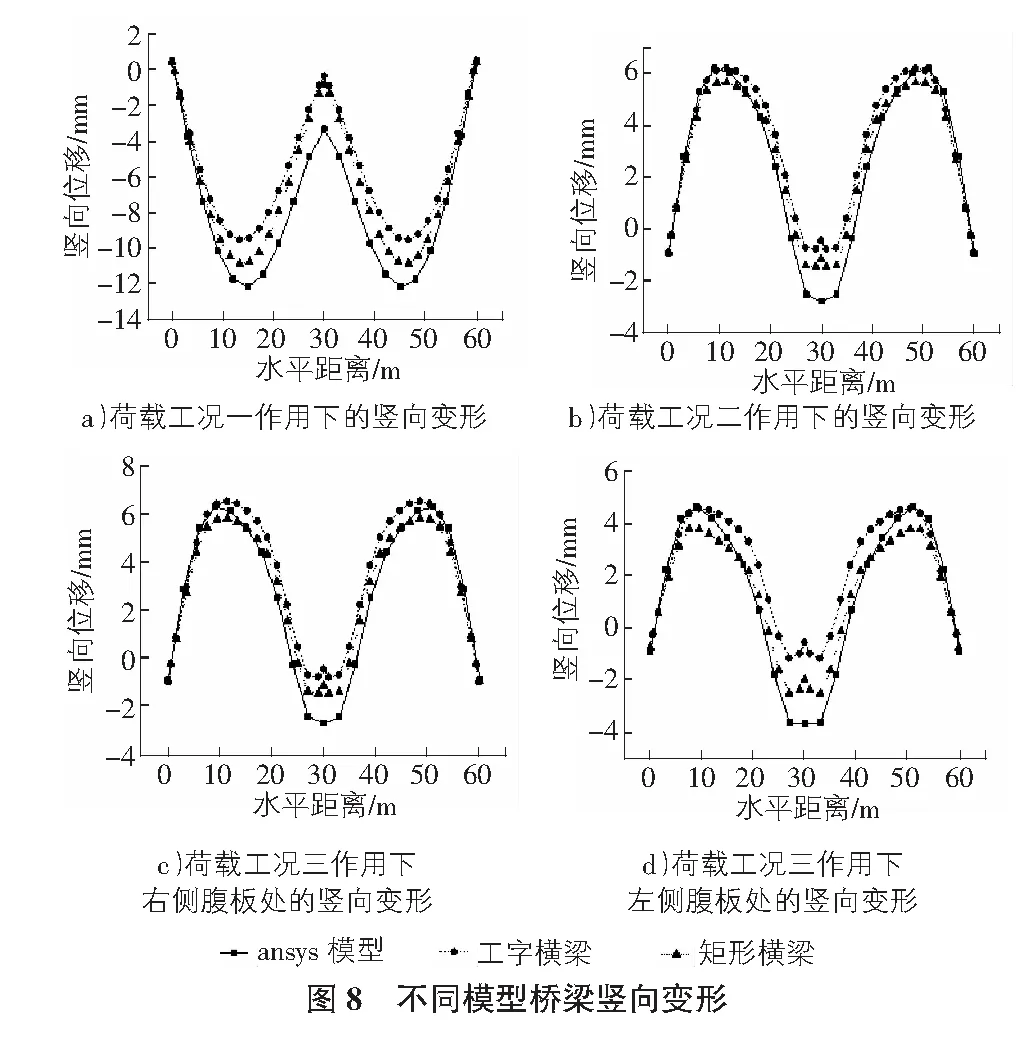
各荷载工况作用下，不同模型桥梁跨中竖向变形的计算结果如图8所示。

由图8竖向变形曲线可以看出：在工况一作用下，工字横梁计算结果差值偏大，矩形横梁计算结果更准确一些；工况二跨中竖向变形差值：采用工字横梁为3.0%，矩形横梁为6.1%；工况三跨中竖向变形差值：右侧腹板采用工字横梁为3.8%，矩形横梁为4.9%，左侧腹板采用工字横梁为1.3%，矩形横梁为9.9%。其中，在荷载工况二、三作用下，工字横梁计算结果差值较小，工字形横梁优于矩形横梁。

5 梁格单元尺寸大小对计算结果的影响

一般来说，纵向梁单元的大小决定横向梁格的疏密程度。纵桥向梁单元尺寸过大使横向梁格稀疏，导致横向联系减弱，影响力的横向传递，相邻纵向梁单元的内力产生跳跃，导致结果失真。单元尺寸过小又导致横向梁格密集，大大增加工作量，费时费力，对计算精度的提高作用不大。通过不同单元尺寸模型的分析比较，梁格单元尺寸的划分应满足以下几点要求：

1)纵向梁格尺寸划分为1 m～2 m可保证精度要求。

2)为保证荷载的正确传递，纵向梁格尺寸不宜超过横向梁肋的间距。

3)单元大小不能超过相邻两个反弯点间距的1/4，在支点附近应适当加密[3]。

6 结语

通过梁格划分方式、横梁模拟方法及梁格单元尺寸对梁格法计算精度的影响分析，得出以下结论：

1)对于箱形截面，纵梁截面易采用等分顶、底板的方式划分，其计算结果精度更高。

2)横向梁格的截面形式宜采用工字形截面，计算精度较高。

3)梁格单元尺寸以保证纵横梁格单元比例相近为宜。