土体本构模型对软土场地基坑开挖模拟结果的影响分析

陆 鸿 斌

(同济大学，上海 200092)

0 引言

随着近年来我国经济的飞速发展，以沿海城市为代表的许多大中城市的发展和建设迎来了新的高潮，而地下空间的开发和利用成为了这些城市发展的新方向，各式各类的深基坑工程在沿海城市的软土场地上不断呈现[1]。由于城市用地十分紧张，这些深基坑工程往往紧邻周围建筑物或交通干线，而基坑开挖会导致基坑周围土体的应力释放，对周围环境产生很大的影响，稍有不慎，便会造成严重的安全事故，带来极大的经济损失和人员伤亡。因此，对基坑开挖过程中由于卸荷作用导致的周围土体的变形规律进行研究，以防止基坑工程施工对周围环境的影响是一项非常重要的工作。

随着近年来计算机技术的不断发展，通过数值模拟的方法对深基坑工程的开挖过程进行模拟成为了一种有效的分析方法。而在模拟过程中，合理的选择土体的本构模型是一个非常关键的问题，它将直接影响到模拟结果的准确性。因此，本文结合上海软土场地某深基坑工程，通过大型通用有限元软件ABAQUS模拟了该基坑开挖的整个过程，分别采用线弹性模型、摩尔—库仑模型及修正的剑桥模型进行计算分析，对不同土体本构模型下的模拟结果进行了对比分析。

1 工程实例

本文以上海软土场地某深基坑工程[2]为研究对象，该基坑平面尺寸约为12 m×100 m，基坑的开挖深度为15.6 m。该基坑围护结构采用地下连续墙+内支撑系统，地下连续墙厚度为1.0 m，深度约为35 m。支撑系统为一道钢筋混凝土支撑外加三道钢支撑，其中首道支撑为钢筋混凝土支撑，布置在地下-1.8 m处，三道钢支撑则分别设置在地下-4.8 m,-8.6 m及-12.2 m处，钢支撑采用的是φ609×16 mm钢管。

该基坑工程所处场地的土体分层情况为：①杂填土，厚度为1.5 m；②粘土，厚度为2.5 m；③淤泥质粉质粘土，厚度为4 m；④淤泥质粘土，厚度为7 m；⑤粘土，厚度为10 m；⑥粉质粘土，厚度为6 m；⑦粉质粘土，厚度为3 m；⑧粉细砂，厚度为10 m；⑨粉砂，厚度为12 m；⑩细砂，未穿。土体的主要物理力学参数如表1所示。

地下连续墙及钢筋混凝土支撑的物理力学参数如下：弹性模量E=3.0×104MPa，泊松比μ=0.30。钢支撑的物理力学参数如下：弹性模量E=2.1×105MPa，泊松比μ=0.20。

2 土体本构模型

2.1 线弹性模型

表1 土体主要物理力学参数

线弹性模型通过理想化的应力应变关系对土体的特性进行描述，对于应力水平较低且边界条件一定时具有一定的适用性。该模型遵循胡克定律并假定土体的应力与应变之间的关系成正比，形式较为简单，且具有以下基本假定：

1)土体材料为各向同性；

2)应力应变关系一一对应；

3)简单应力情况下，材料本构关系为：

σx=Eεx

(1)

εy=εz=-vεx

(2)

其中,E为弹性模量,v为泊松比。

2.2 摩尔—库仑模型

摩尔—库仑模型[3]综合考虑了胡克定律和库仑破坏准则，是一种理想的弹塑性模型。该模型共有5个参数，其中弹性模量E和泊松比v控制弹性行为，粘聚力c、内摩擦角φ和剪胀角ψ控制塑性行为。其屈服函数为：

τ-σtanφ-c=0

(3)

其中，σ，τ分别为剪切面上的正应力和剪应力。

摩尔—库仑模型能较好的描述土体的破坏行为，但由于其破坏前的本构关系是弹性的，因此无法很好地描述土体的非线性变形特征，也无法对应力路径对土体产生的影响加以考虑。然而，由于该模型形式简单，参数少且具有大量的工程经验，因此在岩土工程中的应用也较为广泛。

2.3 修正的剑桥模型

修正的剑桥模型由Roscoe等[4]提出并改进，该模型为等向硬化的弹塑性模型，能准确的描述岩土体的弹塑性变形特征，尤其可以很好的对土体在破坏之前的非线性行为进行模拟，并可以考虑应力路径对土体产生的影响。该模型的破坏方程如式(4)所示，屈服轨迹如图1所示。

(4)

3 计算模型的建立

由于本文中的基坑模型为长条形，因此在建模时可将三维问题简化为平面应变问题进行考虑。为减小边界条件的影响并尽可能模拟工程实际情况同时兼顾计算效率，根据文献[5]中的建议，本文中基坑开挖影响宽度按照3倍的开挖深度考虑，竖向深度方向影响范围取为3倍的开挖深度，即模型尺寸为100 m(宽)×50 m(高)，在数值模拟中取位移边界条件：在模型的底部将各方向位移全部约束，顶部为自由面，模型横向约束水平位移。土体本构模型分别采用线弹性模型、摩尔—库仑模型及修正的剑桥模型进行计算。土体、地下连续墙均通过四节点平面应变单元CPE4模拟，支撑则通过梁单元B21进行模拟。计算模型及网格划分如图2所示。

根据该基坑的开挖过程设置多个分析步，如下所示：

1)地应力平衡分析步，此时土体自重下的位移清零，产生初始应力；

2)基坑开挖至-3.0 m，并施加第一道钢筋混凝土支撑；

3)基坑开挖至-7.0 m，并施加第一道钢支撑；

4)基坑开挖至-10.5 m，并施加第二道钢支撑；

5)基坑开挖至-15.6 m，并施加第三道钢支撑。

4 计算结果分析

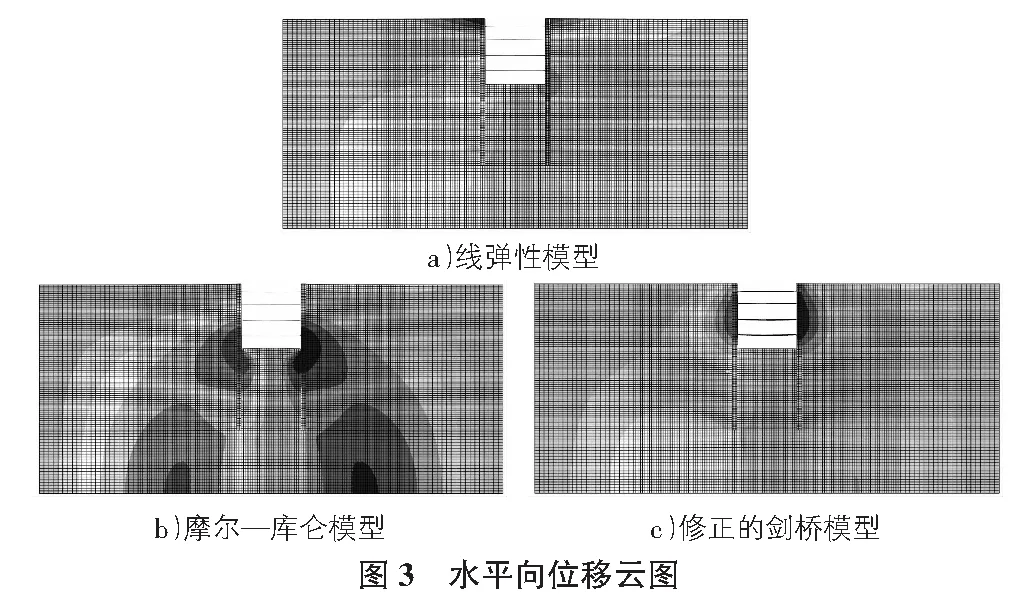
分别以线弹性模型、摩尔—库仑模型及修正的剑桥模型对上海软土场地进行模拟，得到的开挖完成后的基坑水平及竖向变形云图如图3，图4所示，由图中可知，对于水平位移，三种模型计算出来的结果差别较大，其中线弹性模型地下连续墙水平位移呈现上部大，下部小的情况，这明显与工程实际情况是不符的；摩尔—库仑模型地下连续墙的最大水平位移虽然出现在地下连续墙中部，但其位于基坑底部，这与工程实际情况也是有差别的；而修正的剑桥模型地下连续墙的最大水平位移出现在开挖基坑的中部，与实际情况相符。对于竖向位移，在三种本构模型下基坑底部均出现了较大的隆起，且三种情况下的最大竖向位移均出现在基坑底部的中部，与实际情况相符。

为进一步分析不同本构模型对基坑开挖水平位移和竖向位移模拟效果的影响，本文提取了三种土体本构模型情况下基坑开挖结束后地下连续墙沿深度方向的水平位移情况及坑底隆起情况的模拟结果，并与实测结果一同绘制在图5及图6中。

由图5可知，修正的剑桥模型对地下连续墙水平位移的模拟结果最好，地下连续墙沿深度方向水平位移的走势与实测结果基本一致，且最大值出现的位置与实测结果相同，均在地下-12 m附近。线弹性模型对于地下连续墙水平位移的模拟结果与实测结果相差较大，最大水平位移出现在顶端，模拟效果最差。摩尔—库仑模型对地下连续墙水平位移的模拟结果一般，虽然其水平位移走势与实测结果大致相同，呈现先增大后减小的趋势，但其最大值出现在地下-15 m处，与实测结果有一定差别。

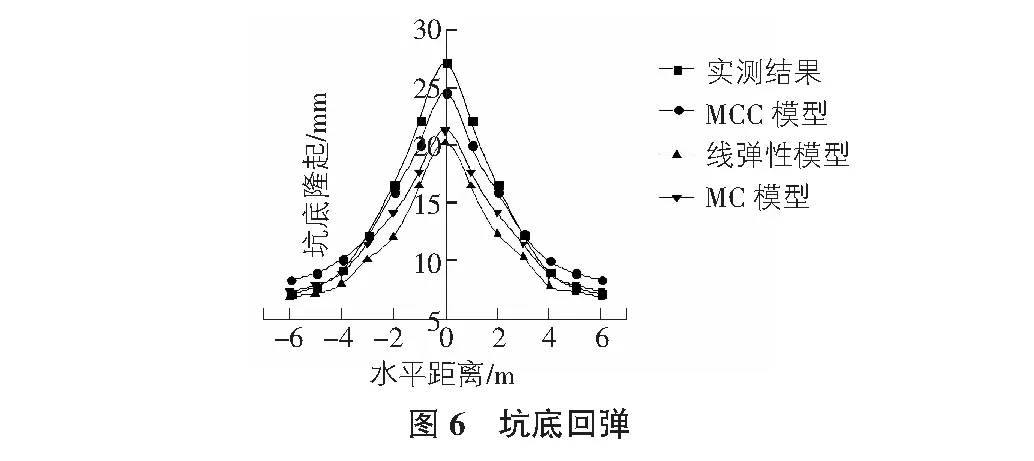
由图6可知，三种本构模型对坑底隆起的模拟结果走势基本一致，模拟效果相差不大，其中线弹性模型模拟结果最小，摩尔—库仑模型模拟结果次之，修正的剑桥模型模拟结果最大，且与实测结果最为接近。

5 结语

通过本文的研究，可得到如下结论：

1)线弹性模型和摩尔—库仑模型对基坑开挖水平位移的模拟结果与实测结果相差较大，模拟效果不好，而修正的剑桥模型对基坑开挖水平位移有较好的模拟效果；

2)三种本构模型对坑底隆起的模拟效果相差不大，且修正的剑桥模型与实测结果最为接近；

3)不同的动力本构模型对软土场地深基坑工程的模拟结果影响较大，对于软土场地深基坑工程开挖的数值模拟，建议选用修正的剑桥模型。