CFRP钢筋混凝土梁塑性铰长度计算

宋勇辉 邹仁华 张 浩 李志凯

(西安科技大学，陕西 西安 710054)

0 引言

国内外学者在CFRP材料以及CFRP加固钢筋混凝土结构等方面，已经有了大量的研究成果，但是对于CFRP加固钢筋混凝土结构的塑性铰的研究还很少见。本文将钢筋混凝土塑性铰长度的理论计算方法[1]引入CFRP加固构件塑性铰长度的计算，并利用有限元进行建模验证分析。

1 CFRP钢筋混凝土梁塑性铰的研究

1.1 CFRP钢筋混凝土梁工作机理

CFRP加固钢筋混凝土梁的破坏通常会出现这两种现象：一是碳纤维布未达到许用拉应变，受压区混凝土被压碎；二是碳纤维布达到许用拉应变，受压区混凝土未被压碎。本文仅对出现第二种情况的CFRP钢筋混凝土梁的工作机理进行分析。

由试验可知，CFRP加固钢筋混凝土梁正截面的应力应变关系发展可分为三个阶段，如图1所示[2]。

第一阶段为弹性阶段，从开始加载到梁构件即将出现裂缝；第二阶段为带裂缝阶段，从混凝土开裂到受拉钢筋即将屈服；第三阶段为破坏阶段，从受拉钢筋屈服到截面破坏为止。在第三阶段中，钢筋应力维持在屈服强度不变，拉应变增加很快，裂缝急剧开展，混凝土受压区高度缩小，压应力图呈明显丰满曲线形。最终因为受压区混凝土的压应变达到极限值，从而截面破坏。

1.2 塑性铰的特征

以受拉钢筋首先达到流限为标志的塑性铰称之为弯拉铰[3]。相关试验证明，受拉钢筋开始屈服到受压区混凝土破坏的过程，梁构件的塑性变形也会在一定的区域内发展。非弹性变形的集中发展，使结构的挠度和转角迅速增大，故此将非弹性变形发生的区域理想化为铰链，即塑性铰，该区域的长度称之为塑性铰长度[4]。

2 CFRP钢筋混凝土梁塑性铰长度的计算

2.1 计算假定及材料的本构关系

以单筋矩形截面的钢筋混凝土简支梁为例，将CFRP利用结构胶粘结在梁底部，具体如图2所示。

由于CFRP钢筋混凝土梁组成材料的复杂性，以及不同材料所表现出力学性能的差异，使得结构受力分析变得复杂。为了简化计算，做如下假设：

1)梁的受力钢筋具有明显屈服点，为适筋梁；

2)当钢筋开始屈服时，CFRP钢筋混凝土构件上部受压区边缘混凝土的应变达到初始屈服点ε0；不考虑混凝土的抗拉强度，忽略结构胶的抗拉、抗压能力和箍筋的约束效应；

3)CFRP钢筋混凝土梁受弯过程中，对相对值较小的τ(剪应力)和σ(正应力)忽略不计；

4)CFRP与梁构件未出现相对滑移，且变形规律符合“平均应变平截面假定”。

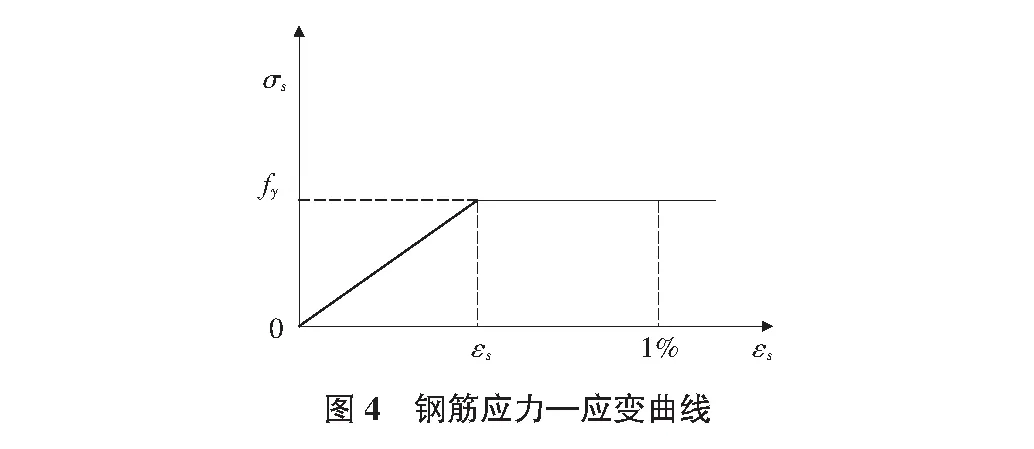
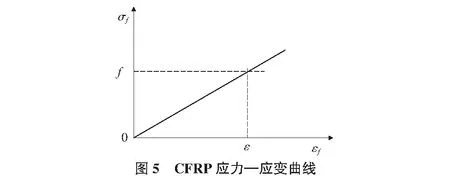
CFRP、钢筋和混凝土材料的本构关系，采用规范推荐的混凝土单轴受压的应力—应变曲线，如图3～图5所示。并给出其相应的计算公式,即：

混凝土构件：当0<ε≪ε0时：

(1)

当ε0<εc≪εu时:

σc=σ0

(2)

钢筋相应的计算公式：

(3)

其中,εy为钢筋的屈服应变。

CFRP布：

采用理想弹性模型，当0<εf<εf,u时:

ff=Efεf

(4)

其中，εf,u为极限拉应变，其值不大于0.01。

2.2 计算公式推导

以单筋矩形截面适筋梁计算为例,假设此时截面钢筋已经屈服，受压区高度为xc，应变处距中和轴的距离为x0(见图6)。

则距离中和轴为y处的混凝土纤维压应变εc为:

(5)

此时，混凝土的应力表达式可以改写为：

(6)

受压区混凝土的合力C：

(7)

钢筋和CFRP承受的总拉力T:

T=Ts+Tf

(8)

其中，Ts=fyAs;Tf=ffAf。

根据弯矩平衡，即∑m=0，可有：

(9)

将式(2)代入式(5)中可以得到：

(10)

(11)

根据力的平衡原理可得出条件C=T，由式(8)、式(11)可得：

(12)

将式(12)代入式(10)可以得出：

(13)

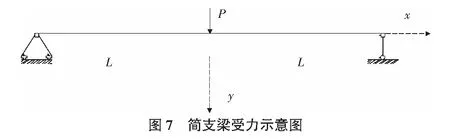
在跨中作用集中荷载P，如图7所示，梁上任一截面的弯矩方程为：

(14)

(15)

在受拉钢筋将要屈服时的截面，将x0=xc代入式(7)可得出：

(16)

同理根据C=T，可得出：

(17)

将其代入式(10)，从而化简可以得出：

(18)

由式(14)、式(15)可得出：

(19)

可得出式(18)、式(19)等价：

(20)

其中，T为钢筋和CFRP承受的总拉力，其值由式(8)得出。

通过化简可得，即全梁最大塑性铰长度：

3 实例验证

3.1 模拟构件的参数

其余参数，根据《混凝土结构设计规范》以及文献[5]确定，具体取值如表1所示。

表1 有限元模型中材料的相关参数

3.2 建立有限元模型

模型相关的单元规定：

1)混凝土单元选用三维实体模型，其本构关系如图3所示，并参照文献[6]选择C30的塑性损伤模型。2)钢筋单元选用三维桁架单元T3D2,将构件中的纵筋和箍筋组为整体钢筋笼进行分析，其本构关系如图4所示，为理想弹塑性模型。3)CFRP布的本构关系为线弹性单元，如图5所示，建模选用三维膜单元M3D4R。模型中添加垫块的参数设定，弹性模量为2.1×106MPa，泊松比为0.3。4)相互作用的确定：钢筋笼内嵌于混凝土构件中，垫块和混凝土构件之间、CFRP布和混凝土构件之间都采用绑定的方式。5)位移加载法，设置参照点并耦合在上部的垫块处，施加集中荷载。

3.3 计算结果分析

基于塑性铰特征理论，加载后，构件下部受拉钢筋达到屈服时，中间失效单元格个数与上部受压区混凝土达到极限破坏时中间失效的单元格数的差值，即为模型计算的塑性铰区长度，记为xAY。将其与理论计算的塑性铰长度x进行对比，如表2所示。

表2 塑性铰长度对比分析

根据表2相关数值显示，可得出两者误差在10%以内。可证明，此次提出的受力简单的CFRP加固混凝土简支梁塑性铰长度的计算方法可行。

4 结语

本课题通过学习规范和相关学者研究成果，从而得出CFRP简支混凝土梁塑性铰长度的计算。其所得的研究主要针对处理一些简单受力的模型，从而得到其理论解为后期相关研究提供参考。为验证本课题理论计算的准确性，为此利用ABAQUS分析软件进行验证。本课题阐明了CFRP混凝土简支梁塑性铰和塑性铰区域的相关定义，为以后研究更加复杂条件下相关数值的计算打下坚实的理论基础。