基于谱聚类三维模型集一致性分割算法
2019-11-18张建刚
贾 晖,张建刚
(1.西安邮电大学 计算机学院,陕西 西安 710121;2.西安热工研究院有限公司 电站信息及监控技术部,陕西 西安 710032)
1 概 述
三维模型分割是根据模型的几何特征将模型分解成为一组数目有限、各自具有简单形状意义且各自连通的子部分[1]。单个模型由于分割尺度的不同造成分割结果的不一致,难以实现模型重用。模型集一致性分割是指同时对一组形状相关但姿态有差异的三维模型集进行分割,得到语义相关分割结果的分割方法[2]。一致性分割算法能得到同尺度的分割结果,算法具有实用性,在快速建模[3-5]及三维数字模型重建中应用广泛[6-8]。
文献[9]提出了基于网格Laplace和K-Means聚类的三维几何模型分割算法,得到模型的归一化形式,用K-Means算法进行聚类,克服了由于姿态变化对模型分割的影响,减少了分割时间,得到了有意义的分割结果。然而分割边界不够整齐,存在K-Means算法的所有问题。文献[10]提出一种基于蚁群优化的网格分割方法,将待分割网格的每个三角面片视为一个蚂蚁,通过蚁群优化迭代对分割标签进行更新,直到达到分割条件实现网格分割。由于蚁群算法具有潜在的平行处理特性,能在一定程度上加快分割速度。然而蚁群算法收敛速度较慢,容易陷入局部最优解,造成过分割现象。文献[11]提出基于Laplace 谱嵌入和Mean Shift聚类的网格一致性分割算法。为了减少姿态变化对三维网格模型的影响,将模型转化成高维谱域中的标准型,并用Mean Shift算法进行聚类,获取模型的分割部位。该算法对于有明显分支结构的模型分割效果较好,但Mean Shift聚类中迭代初始点随机选择,不利于形成较好的分割结果。
以上算法都是无监督的自动聚类算法,除此之外也有采用半监督的方法来实现模型分割。文献[12]提出了一种基于半监督K均值聚类和带状区域增长的三维网格模型层次分割算法,首先提取显著特征点来代表模型的主要分支,利用半监督K均值聚类对模型进行预分割,最后利用离散高斯曲率逼近,采用带状推进区域增长法对模型进行精细化分割。
从以上的分析得出,聚类算法是模型分割的主流方法。监督性聚类算法结果较准确,但却需要大量的人工参与,并未成为分割方法的主流。而聚类算法中的半监督聚类和无监督聚类算法应用最为广泛。算法中所采用的形状描述子大多都基于模型的表面特征(如曲率、法线方向、平均测地距离[13](AGD)等)描述模型之间的形状,并对模型进行分割。而模型的表面特征容易因为类似模型的不同姿态的变化而发生显著变化,并且它们的计算容易产生误差,使其丧失模型间形状可比性。因而采用表面特征不利于在具有形状相似而姿态存在差异的模型集上进行一致性分割。
文中研究模型集上的一致性分割。采用形状直径函数[14](SDF)特征及谱聚类方法对整组模型集进行一致性分割。将三维模型看作带权无向图,面片看作图的节点,面片与面片之间的特征相似性关系看作图的边。将面片的分割问题,看作图的分割问题。首先提取模型集中各个模型面片的SDF特征;其次计算面片特征之间的相似性矩阵,用测地距离进行相似性矩阵稀疏化;最后采用谱聚类对三维模型进行分割。
2 形状直径函数
形状直径函数最早由Shapira在研究模型分割和骨架提取时提出。该特征不是模型的表面特征而是基于模型体特征的形状特征,具有当模型姿态发生变形时,同一部位的特征值基本保持不变的特点,非常适用于具有不同姿态但形状相似的模型之间的部位相似性计算。
如图1所示,SDF特征的计算方法如下:对于三角面片上的每一个顶点,从该顶点以法线反方向为轴做圆锥。在圆锥内部,从顶点向三角面片的另一侧发射射线。计算射线的平均长度rm和长度标准差σ,定义有效射线的范围range。对于每一条范围内的射线rj∈range,定义权重ωj=1/αj,αj是rj与圆锥轴的夹角。顶点的SDF值计算公式为:
(1)
每个三角面片的SDF值的计算方法是首先利用式1计算各面片重心点的SDF值,其次利用式2进行归一化,获得面的SDF值。其中α为归一化参数。
(2)
SDF值在模型的变形中基本保持不变,因为SDF的定义跟模型的体相关而与表面特征无关。同样,不同模型的类似部位同样也具有相似的SDF值,因为类似部位具有相似的体特征,如牛的腿和狗的腿体特征相似。如图2所示。SDF特征对平移、旋转、简化、姿态变化具有很好的鲁棒性,可使用SDF值对同一模型的不同变形以及相似的模型进行一致性分割。
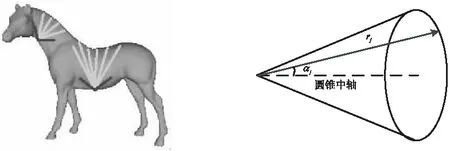
图1 SDF特征值计算

图2 SDF特征分布
3 基于SDF特征的谱聚类分割算法
文中提出一种基于谱聚类的三维模型集一致性分割算法。谱聚类算法建立在谱图理论之上,定义图G=
在图G=
损失函数为:
其中,W为邻接矩阵,即节点之间的相似性关系;D为对角矩阵。
文中将谱聚类应用于三维模型集的一致性分割。将待聚类模型视为带权无向图。图的顶点为待聚类的面片,图的边权为面片之间的相似性关系,边权矩阵被称为相似性矩阵。利用谱图理论分析该无向图,找出分类结构。
在多种聚类方法中谱聚类是最好的无监督聚类算法之一。谱聚类方法有两个优势:谱聚类具有能在任意形状的样本空间上聚类且收敛于全局最优解的优点,不像K-means聚类要求样本空间是凸集;只要相似性矩阵是稀疏的,即使对于高维数据,谱聚类算法的执行效率也非常高。算法步骤如图3所示。
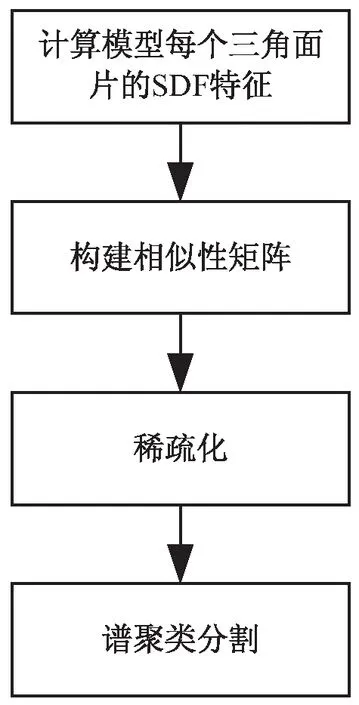
图3 算法步骤
3.1 相似性矩阵
模型面片之间的相似度计算结果将显著影响谱聚类算法的准确性和有效性。面片距离越近,属于一类的概率越高,距离越远,属于一类的概率越低。模型体特征越接近,属于一类的概率越高,体特征差异越大,属于一类的概率越低。参考图像分割中计算像素的相似度方法[15],采用式3计算面片之间的相似度:
(3)
其中,wij为面片i和面片j的相似度;σI为SDF特征的尺度参数。
得到的相似性矩阵为:
(4)
3.2 稀疏化
相似度计算可得三维模型中任意两个三角面片的相似度。若模型中所有面片的个数为n,则W为n×n维矩阵。任意两个面片之间都能计算相似性,此时图为n个节点的完全图。对完全图进行简化才能提高其可分性。
SDF特征描述模型体特征。然而,有些不同部位却有着相似的体特征。如图4(a)的小狗模型,尾巴和腿SDF特征类似。在实验中,如果直接用式4进行聚类,则会产生大量的错分,使得尾巴和腿被分为一类。根据常识,距离越近属于一个划分的概率越高。因此,可根据距离信息,将相似性矩阵进行优化。
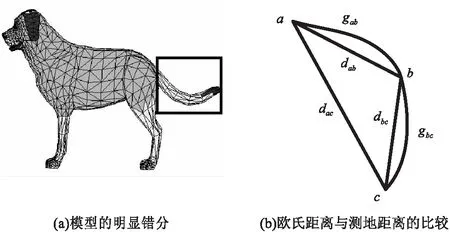
图4 错分和测地距离
为了提高分割的准确度,将完全图中距离过大的面片间的相似性关系去掉,只考虑在一定测地距离范围内的形状相似性,使得相似性矩阵稀疏化。这样既能提高谱聚类的准确性,又能提高计算效率。
测地距离最早用于大地测量,又叫做大地线或者短程线。在三维网格模型上,研究网格顶点或者面片之间的最短距离,称为离散测地距离。测地距离的计算分为精确计算和近似计算两种。应用于三维模型分割中的测地距离计算,大多是近似计算。因为精确计算耗费大量时间,而近似计算耗费时间较小,当网格数量很多时,时间复杂度较低,而计算精度也能满足分割要求,体现出较大的优越性。
有许多经典的求解三维网格上近似测地距离的算法,如Kanai[16]提出的基于带权无向图的三角网格测地距离估算算法等。在Kanai的算法中,三角网格模型被表示为带权无向图,边权用邻接顶点之间的欧氏距离表示。首先利用Dijkstra算法计算带权图上两点间的最短路径,其次以最短路径上的节点为基础,寻找路径上节点的一邻域构建新的带权无向图,在新图中重复使用Dijkstra算法求解最短路径。算法迭代执行,直到满足终止条件。该算法对测地距离的计算较快,但是在网格节点很多的情况下,反复迭代使用Dijkstra算法的时间也很长。
为了能够快速求得三维网格模型中任意两点之间的测地距离,文中对Kanai提出的算法进行简化。基于邻域内欧氏距离是测地距离的近似值的思想,在一个带权无向图中,通过邻域内的最短距离来估算测地距离。这种估计能够达到三维模型分割所要求的计算精度,同时也缩短了计算时间。
图4(b)中a,b,c为曲面上的三个点,这三个点在不同的三角网格上。gab和gbc分别表示节点a与b之间的测地距离。dab,dbc和dac分别表示节点a,b和c两两之间的欧氏距离。从图中可以得出顶点之间的测地距离可由欧氏距离近似计算得到,gab≈dab,gbc≈dbc,gac≈dab+dbc。设三维模型上所有顶点的集合为V,非邻接点的测地距离由以下步骤计算:
STEP1:对三角网格中的每个顶点vi寻找邻接顶点集合Z(vi),且
Z(vi)=vj|vj∈Vandvjis neighbor ofvi
STEP2:在三角网格上计算任意两个邻接顶点间的欧氏距离d(vi,vj),vj∈Z(vi)。
STEP3:求不邻接顶点的最短路径,定义邻接矩阵G:
将计算不相邻两点间的测地距离问题变为在无向带权图上求任意两点间的最短距离问题。利用Dijkstra算法求任意两点vi与vj的最短距离,即为vi与vj的近似测地距离D(vi,vj)。
定义相似性计算距离ri,面片i到其他所有面片的测地距离,取其平均值确定相似矩阵的计算距离。ri=mean(D(fi,fj)),其中j=1,2,…,n。D(fi,fj)为i面与j面的测地距离,以面片顶点间的测地距离的平均值来确定。采用以下方法确定最终的相似性矩阵。
(5)
3.3 三维模型集谱聚类分割算法
输入:三维数据集,相似性矩阵W,聚类数C;
输出:C组聚类。
(1)根据相似性矩阵W计算对角矩阵D,Dii=wi1+wi2+…+win。计算拉普拉斯矩阵L=D-W。
(2)寻找Lu=λDu的特征值λ2,λ3,…,λc+1以及相应的特征向量e2,e3,…,ec+1,则fi为[e2,e3,…,ec+1]中的第i行。
(3)使用K-means算法基于f1,f2,,fC进行聚类分割,将W分割为C组。
4 实验结果与分析
在Windows上,采用一致性分割数据集(COSEG)进行实验,算法运行环境为Intel Core i3 3.3 GHz CPU,4 GB内存。开发平台为Microsoft Visual Studio 2010,图形库为OpenGL。COSEG数据集是具有多个大类的三维模型集,每个模型集中又有若干个类似的三维模型。
以统计数据来评价分割效果。文献[17]定义了面片划分的准确程度的算法,用划分正确面积与模型总面积的比值来计算。式6中l是分割算法得到面片的划分,t是面片真实的划分。由ai表示面片i的面积,δ(li=ti)的取值是当li=ti时δ(li=ti)=1,即为面片划分正确的次数。
(6)
对四足动物、杯子、工具、台灯、椅子以及烛台模型集进行一致性分割,计算算法对每个模型划分的准确程度,并用模型数量进行平均,得到算法对整个模型集的面片平均划分准确率。表1为文中算法对六个模型集的实验数据。不同的模型集的平均面片划分准确率不同。最高的是工具模型集和台灯模型集,准确率都达到了90%;最差的是椅子模型集,准确率达到67%。整体来看,算法的面片平均划分准确率较高,能够较准确地实现模型集分割。

表1 实验模型集平均面片划分准确率
图5为文中算法对六个模型集的分割结果。可以看出,文中算法能较准确地得到模型的部位划分,并且同类模型的分割结果具有一定的对应关系。如台灯模型的三分割中,模型被分成了灯头、连杆和底座。烛台模型集的三分割中,所有的模型被分为火焰、蜡烛和底座。分割中也存在一定的误差,这跟模型的特征值计算误差有关。

图5 文中算法的分割结果
5 算法分析
5.1 实验结果对比
图6为文中算法与文献[13]和文献[18]的分割效果对比。文献[13]采用AGD特征进行模型分割。AGD又称为平均测地距离,是模型的表面特征。网格中某个点的AGD特征含义是曲面上所有点到该点测地距离之和与曲面面积的比值。该特征能够表示网格中某个节点的孤立程度,并且AGD特征的局部极大值体现了模型的末端位置。AGD特征还具有尺度不变性。使用AGD特征进行聚类,能获得一定的部位信息。但从实验结果看,分割结果不够准确。熨斗的手把和熨斗没有完全分开,错分率较高。
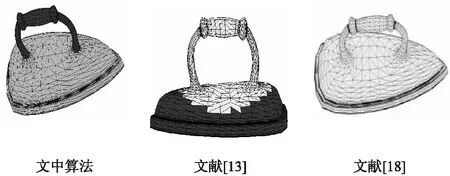
图6 算法比较
文献[18]采用离散曲率作为主要特征。曲率表示曲面的弯曲程度,一般在光滑曲面上计算,在三维网格中需要估算离散曲率。物体的部位分割线往往出现在模型的凹区域。模型某点处的凹凸性取决于该点的高斯曲率K和平均曲率H。通过K和H的正负值来判定曲面的凹凸性,从而提取模型表面凹区域分割线。从实验得出,分割线的提取并未完成区域分割,并且划分部位没有明确的语义含义,需要进行下一步的区域划分和合并才能获得准确的部位分割结果。
文献[13]和文献[18]的分割方法都使用了模型的表面特征。表面特征对噪声敏感,随着计算误差的变化分割结果差异较大;并且这两种算法都不能形成模型集上的一致性分割,对同类模型分割结果没有对应关系。文中算法不但能获得较准确的分割结果,而且对于整组模型的分割部位具有一定的对应关系。因此,文中算法更加适合进行部位重用和快速建模前的预分割。
5.2 鲁棒性分析
模型噪声对分割效果影响严重,在对模型简化的过程中,曲率、距离等几何特征发生了巨大变化。三维模型的面片质量对模型分割有着很大的干扰。经过不同简化处理的模型,大大考验分割的稳定程度。因此有必要对算法在不同简化程度下的鲁棒性进行分析和讨论。
以7号台灯模型为例,该模型顶点数为5 000个,面片数9 996个。对其进行简化,结果见图7(b)和图7(c)。图7(b)顶点2 865个,面片数5 726。图7(c)顶点502个,面片数1 000个。对简化后模型应用文中算法进行三分割,如图7所示。
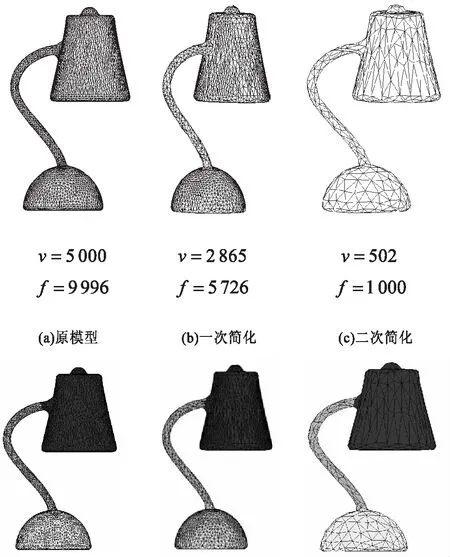
图7 简化模型的分割结果
从分割结果可以看出,随着模型的简化,文中分割算法的分割质量并未明显下降。因此文中分割算法不但具有较高的准确度,对于模型简化也具有较好的稳定度。
6 结束语
文中提出的一致性分割算法首先对选定模型集上的所有三维模型进行SDF特征计算;其次构建相似性矩阵,并用测地距离对相似性矩阵进行稀疏化;最后采用谱聚类对模型集进行分割。实验结果表明,该算法能够对拥有多个具有类似形状模型的模型集进行有意义的一致性分割,面片平均划分准确率较好,并且对于模型简化具有较好的分割稳定度。
另外,在如下两方面还需要继续研究:文中需要人工的设定聚类数量C,不能够根据特征值的变化范围自动确定模型集的分割数;该算法对特定模型能得到较好的结果,但对于体特征不明显的模型不能得到较好的结果,如椅子模型。今后要针对体特征不明显的模型研究通用的模型分割算法。
