基于新阈值函数的小波阈值去噪算法

詹 展，秦会斌

(杭州电子科技大学 新型电子器件与应用研究所，浙江 杭州 310018)

0 引 言

小波变换针对短时傅里叶变换时频局部化精细和灵活性方面的缺点，采用具有时域局域化特性的小波函数作为基底，能自动调节时频窗来满足实际分析中的要求，具有多分辨分析的特点，在信号处理中有广泛的应用。Donoho和Johnstone在小波变换的基础上提出了小波阈值降噪[1]，常见的主要有硬阈值函数和软阈值函数[2]，由于继承了小波分析的优点，实现简单，得到了实际应用。但是硬阈值函数在阈值处是间断的，处理后获得的小波系数用逆小波变换进行重构[3]时会产生伪吉布斯(Pseudo-Gibbs)效应，从而使信号出现失真、震荡现象。软阈值函数的估计小波系数与真实小波系数存有固定偏差。针对这些缺陷，有研究人员提出了与之相关的改进方法，如软硬折中的阈值函数、加权平均法构造的阈值函数、基于粒子群寻优算法[4- 10]等，有一定的改善。

为了克服以上缺点，文中在文献[6]的基础上进行改进，提出一种新的小波阈值函数，有调节阈值因子，能够改善阈值函数的连续性，提高信噪比，减小均方误差，并将其应用到语音增强中，达到了良好的去噪效果。

1 小波阈值消噪

1.1 小波阈值消噪原理

小波阈值去噪法的原理分为3个步骤[7]：对原信号小波分解，确定阈值函数和阈值，小波系数重构。流程如图1所示。

图1 小波阈值去噪流程

1.2 传统阈值函数

传统的阈值函数由Donoho等提出，由于符号函数的特殊数学特性，两种函数表达式组成分别如下：

(1)

(2)

式1为硬阈值函数表达式，其中ωj,k表示小波系数。当ωj,k的数值大于阈值λ时，对ωj,k不做处理，在一定程度上保存了初始信号的噪声分量，产生较大的方差，而且由表达式可以看出函数在±λ处有间断点，使得硬阈值函数在整个函数空间范围内不连续，去噪后的小波系数重构时，会产生伪吉布斯现象。

由于硬、软阈值函数都存在缺陷，为了提高小波阈值函数的去噪效果，学者们基于以上两种方法，提出了一些改进的阈值函数。

文献[6]提出的小波阈值函数为：

(3)

其中，u=1-e-α(|wj,k|-λ)2，α,n为调节因子，且为整数。

式3介于硬阈值和软阈值函数之间，通过改变调节因子在一度程度上能够降低小波系数与估计小波系数的恒定误差，但是还有待进一步改进。

文中提出了一个基于对数函数[8]的改进阈值函数来进一步提升消噪效果。

2 新阈值函数构建

2.1 新阈值函数

针对传统阈值函数存在的各种问题，文中提出一个基于对数的改进阈值函数。该阈值函数不仅能避免传统阈值函数的不足，而且随着小波分解尺度的变化会做出自适应调整。该阈值函数具有调整因子，使用更加灵活，实用性强。其表达式为：

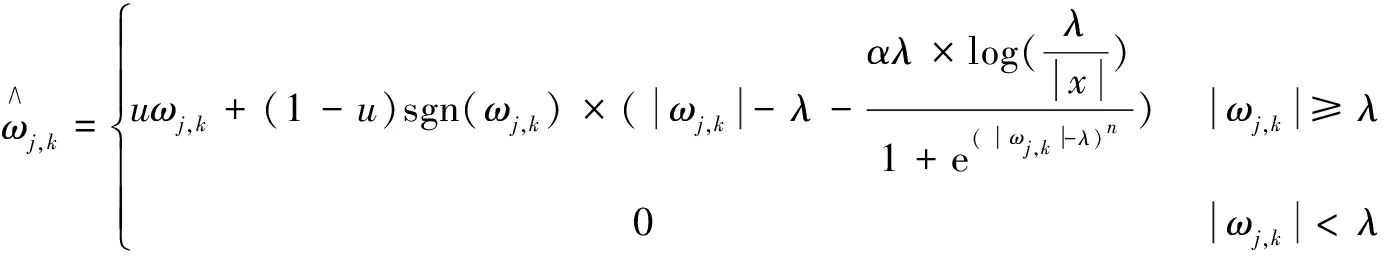
(4)

其中，u=1-e-α(|wj,k|-λ)2，α和n为调节因子，且为整数。

2.2 新阈值函数分析

新阈值函数不但有软阈值函数连续的特点，且当|ωj,k|>λ时函数是高阶可导的，现在从数学角度对式3进行如下分析。

(1)函数的连续性。

在wj,k=λ处：当wj,k→λ+时，

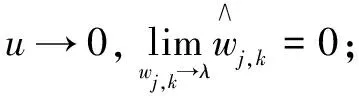
同理也可以证明新阈值函数在wj,k=-λ处也是连续的，证明过程同上。因此新的阈值函数在定义域内连续，还避免了因间断问题导致的伪吉布斯现象。

(2)函数的渐近线。

当wj,k→±∞时，

同时当wj,k→时，

(3)阈值函数的偏差性。

(4)函数的高阶可导性。

新阈值函数定义域内是由符号函数、指数函数和对数函数组成的，它们都是初等函数，根据初等函数可导的性质可知，新阈值函数也是一个高阶可导函数。

(5)阈值可变因子α与n影响分析。

当α→∞时，n→∞，新阈值函数为式1，成为一个硬阈值函数；当α→0时，新阈值函数为式2，变为软阈值函数。因此，只要改变α值，新阈值函数就能够在硬和软阈值函数之间灵活变化。参数α决定小波阈值的逼近程度，在处理带噪信号时能够保留部分高频信号，使细节系数和信号震荡现象能够较好地得到抑制。

2.3 确定阈值和分解层数

合理有效地选择阈值，关系到信号的最终去噪效果[11]。该实验中采用自适应阈值[12]，即：

(5)

其中，σ为噪声方差[13]；N为语音信号的长度；j为当前分解尺度；调节常数C可以得到最佳的输出信噪比。实际应用中，由于σ不确定，一般取σ=median(w)/0.674 5。这种自适应阈值有效克服了固定阈值的缺点，去噪效果较好，且更加顽健。

对于分解层数的确定，采用如下算法：通过改变分解层数，不断循环计算消噪信号的信噪比SNR2与带噪信号信噪比SNR1的差值，取差值最大时的分解层数为最优值。流程如图2所示。

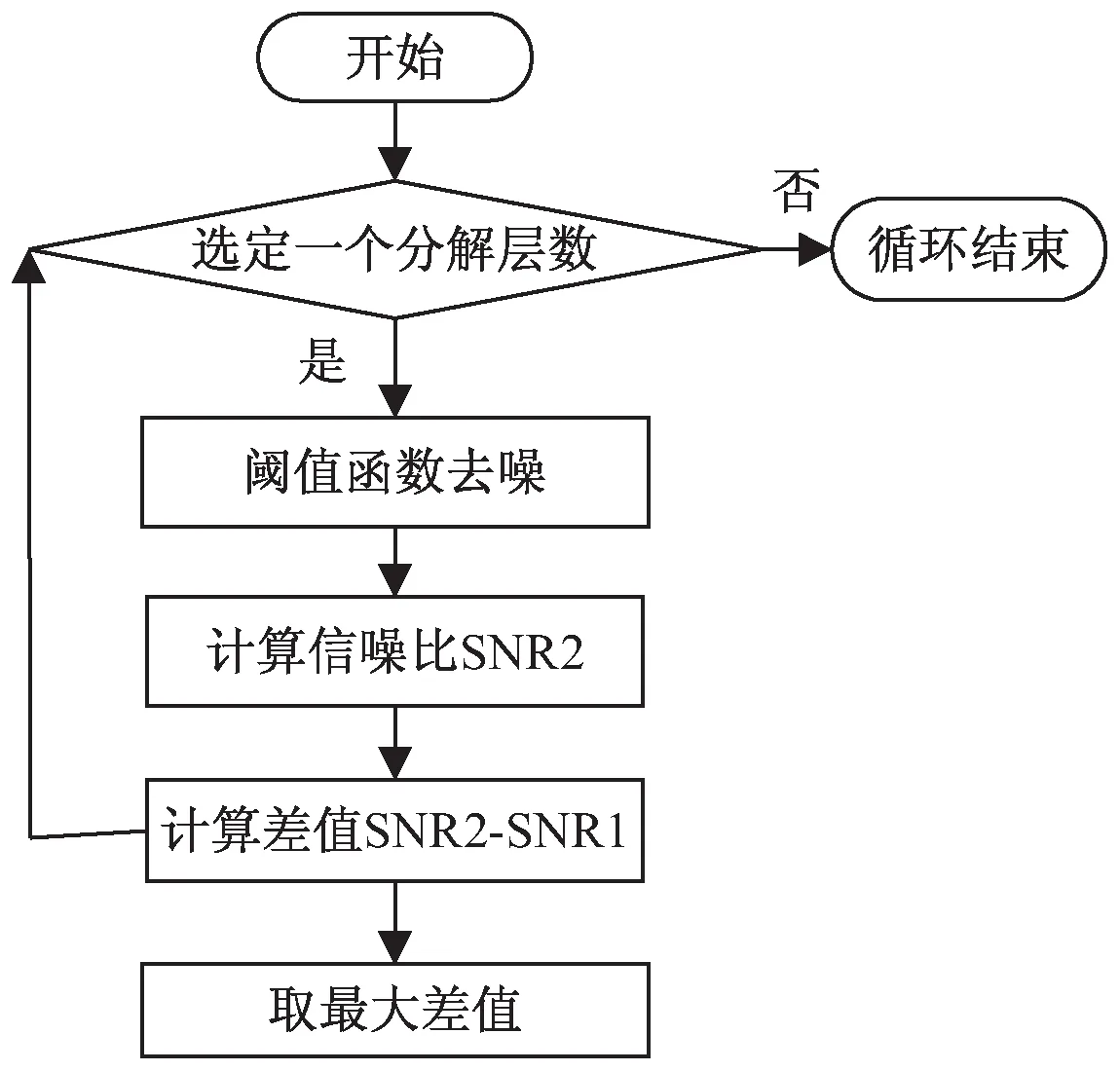
图2 分解层数选择流程

3 仿真实验与结果分析

3.1 去噪效果评价指标

在信号处理时，通常用信噪比和重构信号均方误差对去噪效果进行评价。若信噪比指标越大，而均方误差指标越小，说明去噪效果越好[14-15]。表达式如下：

(6)

(7)

3.2 实验仿真

首先确定分解层数，采用上一节所述算法，选择自适应阈值，通过仿真得到分解层数和信噪比改善量之间的对应曲线，如图3所示。由图3观察可知，分解层数为6时，改善量最大。

图3 分解层数与信噪比改善量曲线

基于以上的去噪评价指标，为了说明提出的去噪算法的有效性，采用传统的硬、软阈值函数，文献[6]中的方法和文中提出的新阈值函数进行对比。用Matlab工具对含噪测试信号bumps和heavysine进行小波去噪实验，对其加入信噪比SNR为6 dB的高斯白噪声，采用小波基为sym6小波，6层分解层数，其中设定式5中C=1，式3、式5中n取3。每个处理结果是30次运算的平均值。下面以含噪bumps信号为例进行说明，去噪效果波形如图5所示，信噪比SNR和均方误差MSE如表1所示。

通过大量的仿真实验，根据所得数据有如下分析：

含噪的bumps和heavysine信号经过各种阈值函数去噪后有很大的差别。由图4可知，经过硬阈值函数处理后的重构信号产生了震荡现象。经过软阈值函数去噪后的信号在阈值处虽然连续，但是不可导，而且处理前后小波系数存在一定偏差，使得波形有明显的萎缩。文献[6]中的阈值函数处理噪声信号后的重构信号光滑且与原始信号很接近，而新的阈值函数比文献[6]中的函数更具有优势，在阈值处不是直接置0而是平滑处理，细节更加逼近原信号，无附加震荡，波形更加平滑。

由表1可知，新阈值函数与其他三个阈值函数相比，信噪比有很好的提高，均方误差也进一步减小。因此，无论是从波形特征还是数据指标来看，均验证了文中提出的阈值函数去噪算法的优越性。

图4 各阈值函数对bumps信号去噪效果

评价指标含噪信号硬阈值函数软阈值函数文献[6]阈值函数(α=1)新阈值函数(α=1)文献[6]阈值函数(α=5)新阈值函数(α=5)文献[6]阈值函数(α=10)新阈值函数(α=10)bumpsSNR/dB16.963 3416.189 4817.311 7221.192 7821.309 4621.516 6021.652 0421.276 1021.431 28MSE0.999 601.092 540.971 200.611 760.610 560.589 320.586 960.606 360.602 46heavysineSNR/dB15.953 0623.711 1424.883 0226.063 1826.192 1626.654 8826.712 1026.751 9426.877 44MSE1.004 800.408 260.355 680.311 220.310 240.290 240.288 360.286 600.285 76

3.3 真实环境下的语音消噪

下面把改进算法应用在语音增强上，验证真实环境下的语音消噪效果。文中采用录制内容为“电子信息学院”的语音作为测试信号。背景噪声采用高斯白噪声，语音信号和噪声采样频率均为8 kHz，单声道，16 bit采样位数。同样采用上述四种算法对语音进行去噪。小波基为sym6，小波分解尺度为6，去噪后信号的时域波形如图5所示。

图5 语音信号去噪效果

图5中，观察原信号的前后端有一些凸起的“毛刺”，该现象是因为在录音过程中引入系统内部等环境噪声引起的。通过改进的阈值函数处理后，不仅在很大程度上削减了噪声，而且“毛刺”也得到了抑制。

除了去噪效果比较以外，还得到了每个函数的信噪比和均方误差，如表2所示。

由表2的数据对比可知，文中改进的阈值函数对语音进行去噪后的SNR比其他几种函数都要高，而且MSE也是最低的。通过以上实验结果可知，相比文献[6]的阈值函数和传统软、硬阈值函数，文中改进的阈值函数的语音消噪效果更加明显。

表2 各阈值函数对语音信号去噪后的评价指标

4 结束语

从原理上分析了硬阈值函数、文献[6]以及软阈值函数的优缺点后，文中提出一种带有调节因子的阈值去噪算法，有很强的实用性和灵活性。先从信噪比、均方误差两方面与其他三个阈值函数作对比，验证改进算法的有效性；最后将算法应用在语音增强，进一步证明算法的可行性。仿真结果表明，该阈值函数相比硬、软阈值函数和文献[6]提出的函数，无论是在测试信号还是语音信号上，都具有更好的去噪效果，在保留有用语音信号的同时，一定程度上提高了语音整体质量，达到了良好的语音去噪效果。