基于人工神经网络的二分类方法

聂文都，蔡锦凡

（西京学院信息工程学院，西安710123）

0 引言

人工神经网络（Artificial Neural Network，ANN）从信息处理的角度对人脑神经元进行抽象，建立一种简单模型，按不同的连接方式组成不同的网络。神经网络是一种运算模型，由大量的节点（或称神经元）之间相互联接构成。每个节点代表一种特定的输出函数，称为激励函数（Activation Function）[1]。每两个节点间的连接都代表一个对于通过该连接信号的加权值，称之为权重，这相当于人工神经网络的记忆。网络的输出则依网络的连接方式，权重值和激励函数的不同而不同。而网络自身通常都是对自然界某种算法或者函数的逼近，也可以是对一种逻辑策略的表达。

相对于传统的线性逻辑回归算法[2]，人工神经网络具有良好的容错性，泛化能力好，适于拟合复杂的非线性关系，应用领域广泛，是当前许多工程领域的研究热点。现在很多问题都是二分类[3-4]问题，现在很多都是利用人工神经网络实现而分类问题。

1 人工神经网络的结构与模型

1.1 生物神经元的结构

神经细胞是构成神经系统的基本单元，称之为生物神经元[5]，简称神经元。神经元主要由三部分构成：①细胞体；②轴突；③树突。生物神经元结构如图1所示。

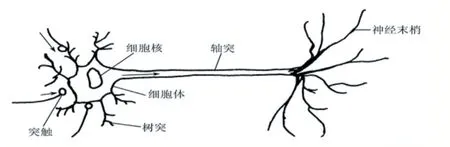
图1 生物神经元结构

神经元的功能特性：①时空整合功能；②神经元的动态极化性；③兴奋与抑制状态；④结构的可塑性；⑤脉冲与电位信号的转换；⑥突触延期和不应期；⑦学习、遗忘和疲劳。

1.2 人工神经元结构

人工神经网络是由大量处理单元经广泛互连而组成的人工网络，用来模拟脑神经系统的结构和功能。而这些处理单元我们把它称作人工神经元[6]。人工神经元结构如图2 所示。

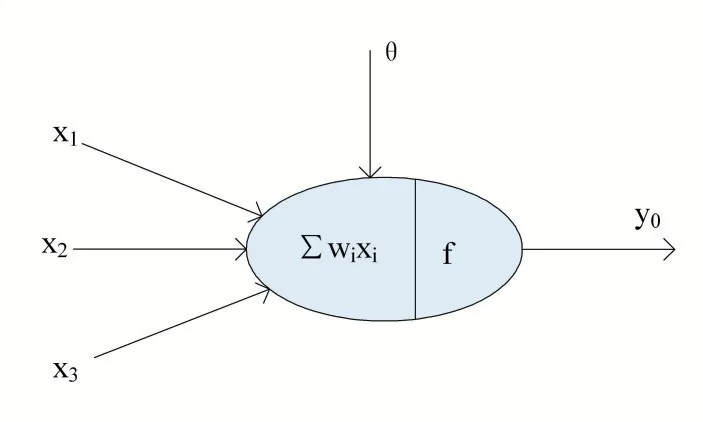
图2 人工神经元结构

神经网络从两个方面模拟大脑：

（1）神经网络获取的知识是从外界环境中学习得来的;

（2）内部神经元的连接强度，即突触权值。用于储存获取的知识。

神经网络系统由能够处理人类大脑不同部分之间信息传递的由大量神经元连接形成的拓扑结构组成，依赖于这些庞大的神经元数目和它们之间的联系，人类的大脑能够收到输入的信息的刺激由分布式并行处理的神经元相互连接进行非线性映射处理，从而实现复杂的信息处理和推理任务。对于某个处理单元（神经元）来说，假设来自其他处理单元（神经元）i 的信息为xi，它们与本处理单元的互相作用强度即连接权值为wi,i=0,1,2,…,n-1，处理单元的内部阈值为θ。而处理单元的输出为：

式中，xi为第i 个元素的输入，wi为第i 个处理单元与本处理单元的互联权重即神经元连接权值。f 称为激活函数或作用函数，它决定节点（神经元）的输出，θ表示隐含层神经节点的阈值。

1.3 人工神经网络模型

一个人工神经网络由多个神经元结构组成，每一层的神经元都拥有输入和输出，每一层都是由多个神经元组成。第i-1 层网络神经元的输出是第i 层神经元的输入，输入的数据通过神经元上的激活函数来控制输出数值的大小。该输出数值是一个非线性值，通过激活函数得到的数值，根据极限值来判断是否需要激活该单元。一般多层人工神经网络由输入层、输出层和隐藏层组成。如图3 所示。

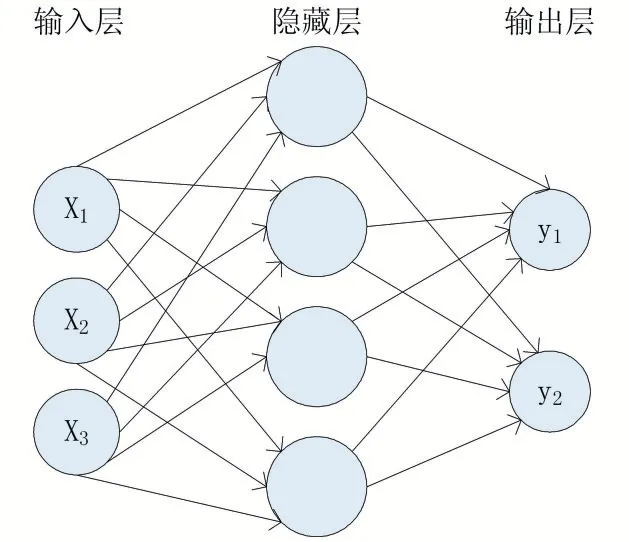
图3 三层人工神经网络模型

输入层（Input Layer）是接受输入信号作为输入层的输入；输出层（Output Layer）是信号在神经网络中经过神经元的传输、内积、激活后，形成输出信号进行输出；隐藏层（Hidden Layer）：隐藏层也被称为隐层，它介于输入层和输出层之间，是由大量神经元并列组成的网络层，通常一个人工神经网络可以有多个隐藏层。

2 人工神经网络的训练与预测

2.1 人工神经网络的训练

首先给所有的权重向量W 和偏置b 赋予随机值，使用这些随即生成的权重参数值来预测训练中的数据样本。样本的预测值为y^，真实值为y，现在定义一个损失函数[7-8]，目标是使预测值尽可能接近真实值，损失函数就是使得神经网络的损失值和尽可能的小。其基本公式为：

使得模型效果最佳就是如何改变神经网络中的参数W 和b，使得损失函数的值最小。

2.2 人工神经网络的预测

在训练阶段，通过算法修改神经网络的权值向量W 和偏置b，使得损失函数最小。当损失函数收敛到某个阈值或者等于零时，停止训练，就可以得到权值向量W 和偏置b。到此为止，人工神经网络模型结构中所有的参数（输入层、输出层、隐层的节点数、权值向量W、偏置b）都是已知的，只需要将向量化后的数据从人工神经网络的输入层开始输入，顺着数据流动的方向在网络中进行计算，直到数据传输到输出层并进行输出（一次前行传播），就完成一次预测并得到分类结果。

3 人工神经网络的核心算法

3.1 梯度下降算法（Gradient Descent Algorithm）

假设函数L（θ）为损失函数，为了找到损失函数的最小值，需要沿着与梯度向量相反的方向更新变量θ，这样可以使梯度减小得最快，直至损失函数收敛至最小值。该算法称为梯度下降算法[9-11]，其基本公式为：

其中，η∈R 为学习率，用于控制梯度下降的幅度（快慢）。在神经网络中，上式中的变量θ是由神经网络的参数所组成的向量θ={w1,w2,…,wn,b1,b2,…,bn}。梯度下降的目标就是找到参数θ*使得神经网络总损失L最小，从而确定神经网络中的权重向量W 和偏置b。梯度下降算法的特点是：越接近目标值，变化越小，梯度下降的速度越慢。梯度下降的算法有很多变种形式，主要有以下三个：①批量梯度下降算法（Batch Gradient Descent，BGD）；②随即梯度下降算法（Stochastic Gradient Descent，SGD）；③小批量随机梯度下降算法（Min-batch SGD）。如图4 所示，（a）批量梯度下降算法的下降轨迹平滑，经过多次迭代后达到全局最优解处；而（b）小批量随机梯度下降算法在下降过程中持续的小幅振荡，但每次迭代的数据量少，能够更快地找到全局最优解。因此小批量随机梯度下降算法在实际工程中使用的频率更高。

图4 BGD 和Min-batch SGD 梯度下降示意图

3.2 向前传播算法（Forward Propagation Algorithms）

向前传播（Feed Forward）算法在神经网络的训练和预测阶段都会被反复用到，是神经网络中最常见的算法。其计算方式简单，只需要根据神经网络模型的数据流动方向对输入的数据进行计算，最终得到输出结果。图5 所示是一个简单的人工神经网络模型[12]，其输入层有两个节点，隐层、输出层均有3 个节点。可以通过矩阵的方式对向前传播算法进行解析。假设zi（l）为第l 层网络第i 个神经元到第l+1 层网络中的第j 个神经元的连接，那么根据神经元基本公式有：

神经网络的参数进行量化[9]，表示为：

因此，单层神经网络的向前传播算法可以使用矩阵表达为：

其中，a（l）为第l 层网络的输出矩阵，f 为激活函数。

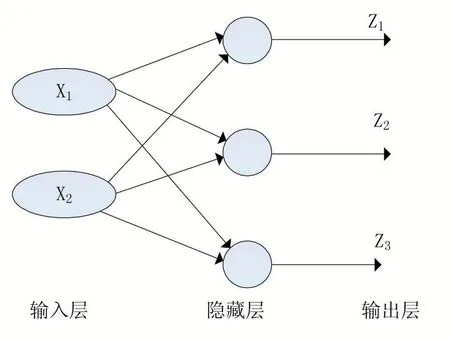
图5 单隐藏层神经网络的向前传播

3.3 反向传播算法（Back Propagation Algorithms）

反向传播算法[13-15]的数学定义是根据微积分里面的一些数学法则来阐述的。假设神经网络模型的参数为θ={w1,w2,…,wn,b1,b2,…,bn}，那么反向传播算法的精髓是：通过链式求导法则，求出网络模型中的每个参数的偏导数。

反向传播算法中最基本的四个方程如下：

BP1 输出层误差：

BP2 第l 层误差：

BP3 损失函数关于偏置的偏导：

BP4 损失函数关于权值的偏导：

其中，定义第l 层的第i 个神经元的误差为L 对z的偏导。▽a为在ail处的梯度，为f 激活函数，w 为权值，b 为偏置。反向传播算法流程是根据四个基本方程进行总结的，具体流程如图6 所示。

图6 反向传播算法流程

4 人工神经网络二分类实验

4.1 实验环境及其相关参数设置

基于华为Matebook-X 笔记本电脑，使用Python 3.6 作为编程开发语言，系统的操作环境为Windows10，硬件开发环境为Intel i5 处理器，8GB 运行内存，CPU 为 Intel Core i5-7200U CPU @2.50GHz 2.71GHz，使用PyCharm 作为神经网络开发框架。此次实验是为了实现医疗数据的二分类，所用到的数据为球菌数据，数据源医疗公共数据集。并用了两种方法实现此二分类，一种人工神经网络，一种线性逻辑回归。

建立一个3 层人工神经网络模型，输入层中的神经元节点数目由输入数据的维数决定，本实验中有链球菌x1，因此输入维度是2，输入有两个神经元节点组成。同理，输出层中的神经元节点数由输出的分类维度决定，本实验中为病原体I（0）和病原体II（1），因此输出层有两个神经元组成。最后可以将此次实验的人工神经网络定义为如图7 所示。

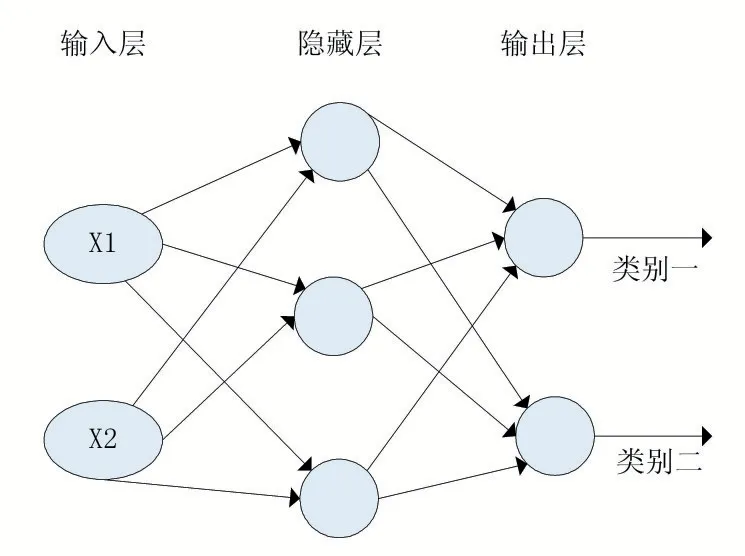
图7 二分类3层人工神经网络

本实验中用到了3 个隐藏层，根据实际情况，我们可以增加隐藏层数和每一个隐藏层的节点数，隐藏层越多，隐藏层节点越多，就能够处理更加复杂的数据模型，但是代价开销大：

（1）隐藏层越多，意味着网络模型越大，参数越多，占用GPU 显存越多；

（2）参数量越多，数据过拟合的可能性越大，网络越有可能不稳定，预测效果反而下降。

4.2 实验结果及其分析

实验结果如图8、图9 所示。

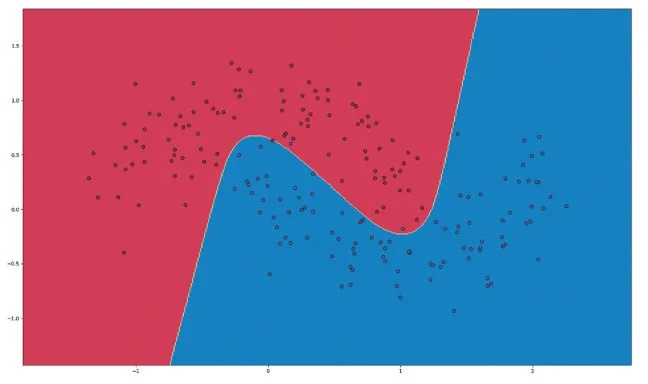
图8 ANN二分类结果

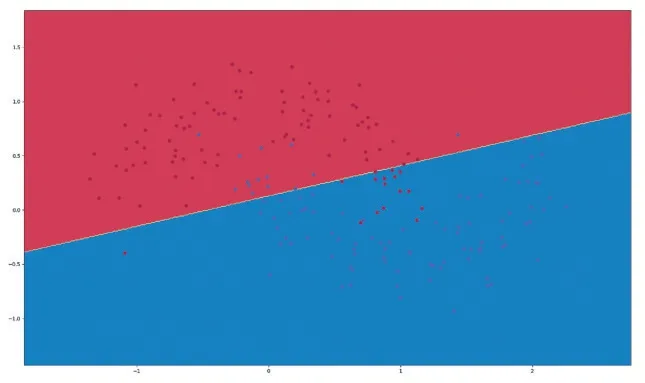
图9 线性逻辑回归二分类结果

实验结果分析：

图8 ANN 二分类实验结果中，错误分类的点较少，分类效果较好；图9 线性逻辑回归二分类实验结果中，错误分类较多，分类效果较差。但是ANN 二分类仍然有一些错误分类的点，可能是隐藏层神经元节点数不够合理，可以适当增加一点隐藏层神经元节点数。但是要注意增加节点数就会使得过拟合的可能性越高，经过代码调试得知，当隐藏层数达到50 层时，过拟合现象就会很严重。本次实验，两种方法上对比分类结果可以看出，ANN 的二分类效果要比线性逻辑回归的二分类效果更好。

5 结语

本文通过对人工神经网络核心算法的介绍，与传统的线性逻辑回归算法进行对比，人工神经网络在处理二分类问题上更优于线性逻辑回归算法。虽然人工神经网络应用非常广泛，也相比传统的算法在二分类问题上更加精确，但是人工神经网络有关参数的计算量大，需要对数据和参数进行优化。对未来人工神经网络的发展和机器人在处理二分类问题上有着一定的帮助。