纳流体忆阻器数学建模及仿真

文/李昕泽

1 纳流体背景简介

离子和分子在纳米尺度下的传输过程引起了大家广泛地关注。由于纳米孔和纳米沟道跟一些生物分子（例如蛋白质，DNA）具有相当的尺寸，因此也开始在生物分子的分离和传感中应用。比如α-hemolysin 就是一种生物纳米孔，可以检测某种单分子物质。但是，这种沟道的缺点是不稳定，很难控制。相反人工无机的纳米沟道是通过在固态衬底上面加工制备的，因此鲁棒性好，柔韧性好，同时纳米尺寸可以精确控制。甚至可以通过微纳制备工艺制备集成的纳米沟道实现系统级功能。纳米沟道的特征尺寸一般比较接近离子的德拜长度(λD)。众所周知，表面电荷可以引起离子选择性和动电效应（包括电泳和电渗）。在微流控器件中，电渗流被广泛地研究，同时用来驱动流体的流动。当沟道的尺寸比较进阶德拜长度时，纳米沟道的表面电荷主导沟道的极性和离子浓度从而控制沟道的离子电导。和微流道中沟道的电渗流不同，纳米沟道中的离子流动主要由表面电荷来决定，不是由于流体本身的流动来决定。

2 固-液界面中静电相互作用

当固态介质和水介质接触时，由于固体表面的水解或者吸引离子，使得固体表面产生表面电荷。由于静电作用，电解质中的壁面电荷会影响附近的离子分布。跟壁面相同电荷的离子会被排斥，相异电荷的离子会被吸引，如图1所示。由于正负离子的随机运动和离子的吸引和排斥形成双电荷层。双电荷层由不能移动的壁面电荷和可以移动的离子组成。这个可以移动离子的电性和壁面电荷电性相反来使得纳米沟道体系达到电中性平衡。这些离子可以在固-液界面附近发生扩散。目前学术界有几种模型来描述双电荷层。Helmholtz 模型描述的双电荷层是一种两个电荷层具有固定距离的物理模型。Gouy-Chapman 模型描述双电荷层是表面电荷和一个溶液中屏蔽离子电荷组成，其中溶液中的屏蔽离子是分散的，因此也被称为扩散双电层。另一个经典模型是结合了前面两种模型的Gouy-Chapman-Stern 模型。溶液中靠近屏蔽离子的电荷层叫Stern 电荷层。引入Stern 电荷层是考虑了离子的直径大小，它限制了扩散层内边界的厚度，如图2所示。在图中可以看到Stern电荷层的电势和固-液界面的静电位非常接近。

3 纳米沟道中离子选择透过性建模及分析

为了更容易仿真，我们把我们的纳米通道近似为一个圆柱体，其长度为 5μm，横截面为半径 50nm的圆，如图3所示。绝大多数的固体表面会因某种机理而产生表面电荷，在宏观体系中，这种表面电荷的影响并不明显，但是在界面的微观体系中，这种表面电荷的存在却具有十分重要的意义。是不能被忽略的。因此我们在我们纳米通道的仿真中把表面电荷的因素加进来。我们纳米通道的壁面为 PDMS，常温下会水解为硅酸盐，硅酸盐电离会带负电荷。使得表面电荷极性为负。

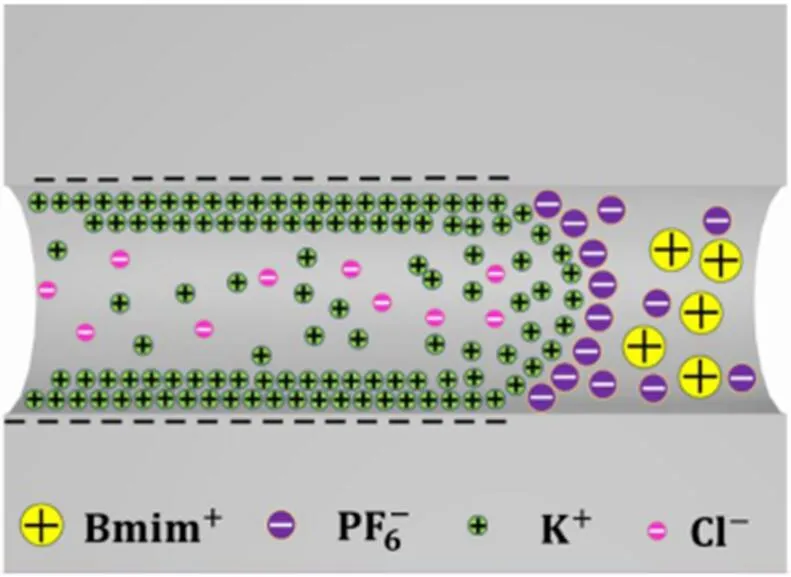
图1：纳米沟道界面离子及壁面电荷分布

图2：纳米沟道壁面附近离子分布示意图

图3：纳米沟道三维模型示意图

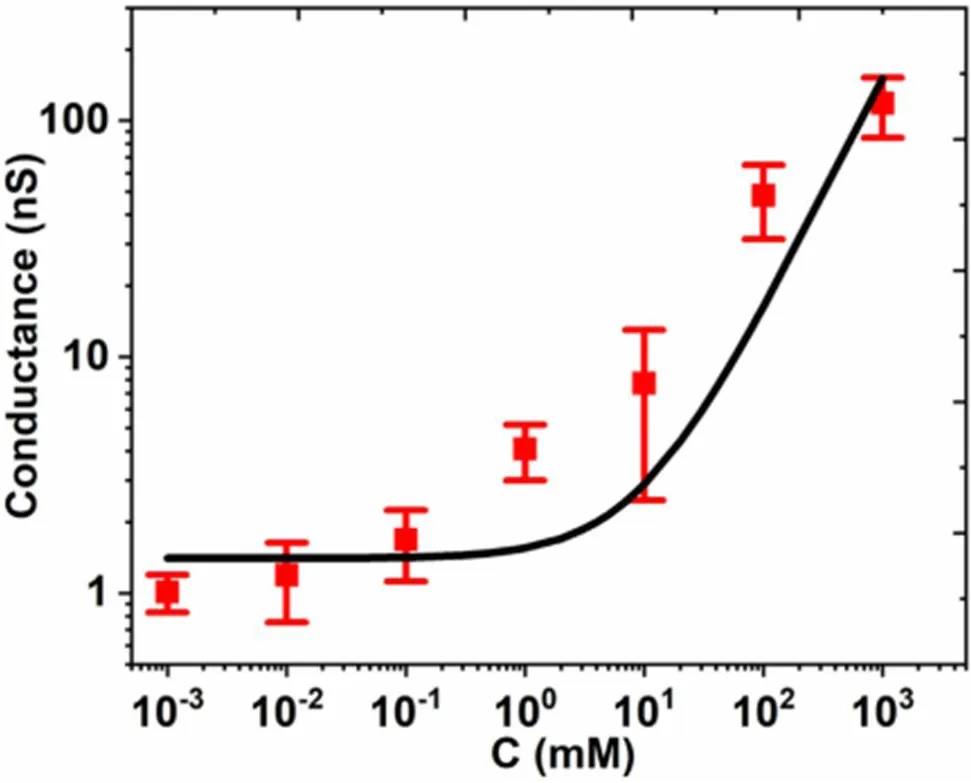
图4：纳米沟道电导随着KCl溶液浓度变化趋势图

使得固体表面附近溶液中单位体积净电荷密度不为零，固体表面电荷与溶液中平衡点和的重新分布形成双电层。电荷密度随着壁面距离的增加而逐渐接近溶液中的电荷密度，因此正电荷会随着距离的增加而慢慢减少，呈扩散状态分布。因此当氯化钾的浓度比较低的时候，几乎需要所有的钾离子移动到壁面来补偿壁面的负电荷，钾离子近似充满通道，扩散层长度很长，因此此时纳米通道的电导主要由表面电荷所决定。随着氯化钾浓度的升高，只需要小部分钾离子就能屏蔽壁面的负电荷，扩散层长度变短，此时纳米通道中的电荷由溶液本身的电荷密度所决定。图4所示为利用电压扫描测量不同浓度电导的结果，我们可以看出氯化钾浓度比较低的时候，电导近似不变，此时沟道内的离子主要由表面电荷引起，沟道内离子浓度高于体溶液，这是典型的双电层引出的反直觉的现象之一。随着氯化钾浓度升高，到达一定浓度后电导出现线性增加，此时沟道内溶液浓度和体溶液近似相等。这个实验现象再次表明在纳米沟道中，其内部电导并不可以简单的直接用G=σS/l计算（G是器件电导，l是纳米沟道的长度，S是纳米沟道的横截面积，σ是纳米沟道中溶液的电导率），而是需要考虑表面电荷对纳米沟道内电导的影响。因此针对这一现象我们建立了一个物理模型，定量的仿出来不同溶液浓度对应的具体的纳米沟道内的电势分布。用MATLAB中的偏微分方程工具箱（PDE Toolbox）求解上述偏微分方程，求出不同浓度的氯化钾溶液对应的纳米沟道的电势分布如图5所示。

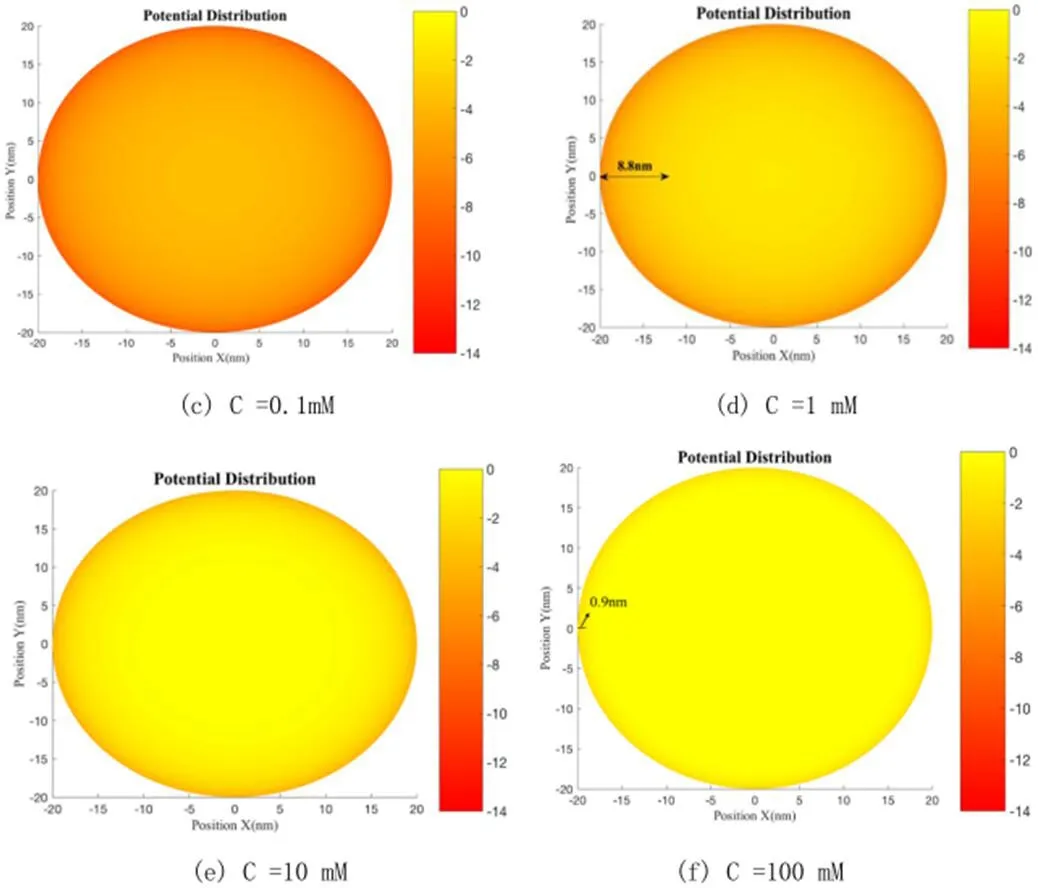
图5：不同浓度 KCl 溶液中纳米沟道截面电势分布

4 总结

主要介绍对纳流体忆阻器进行数学建模。首先对纳流体理论进行详细介绍，强调纳米沟道在纳米尺度下由于表面积和体积比比较大，造成很大的表面电荷密度，这个表面电荷对纳米沟道中的离子传输行为造成影响，这就是纳流体器件应用的理论基础，然后对本文提到的纳流体忆阻器进行详细建模，首先通过不同浓度沟道的电导来计算纳米沟道表面的电荷密度；接着设置纳米沟道中边界条件，计算在电压脉冲条件下，沟道中界面移动的速率和位移，从而计算出每一个脉冲条件下纳米沟道的变化，为纳流体忆阻器的突触行为提供数学支撑，同时也将计算模型结果和实验结果进行对比，发现两者结果非常匹配。最后，由于工艺条件的限制，本文还对纳流体忆阻器在极限尺寸下的工作性能进行预测，发现改变沟道的长度能够有效的提高纳流体忆阻器的响应速度。