基于灰色关联度的自行车间歇训练诱发股直肌疲劳的肌电评价效果研究

王乐军，邵企能，马国强，龚铭新，牛文鑫，邱 俊，徐仰才

（1.同济大学 体育教学部 运动与健康研究中心，上海200092；2.上海体育科学研究所，上海200030；3.同济大学 医学院，上海200092；4.上海中医药大学 体育部，上海201203）

0 前言

在最近十几年，对大强度间歇训练引起机体适应性变化及其机制的探索与研究已引起运动科学界的广泛关注，并在人体运动健康促进和运动训练效果提升等方面起到积极有效的促进作用（Burgomaster et al.，2005，2007；Little et al.，2010；Metcalfe et al.，2012）。在自行车运动中，前期研究发现，通过大强度的速度型间歇训练可以在显著提高运动员无氧能力的同时兼顾有氧能力的发展，已被广泛应用于自行车专项训练（马国强，2014；马国强等，2016）。作为一种大强度的运动训练方法，在自行车大强度速度型间歇训练中，运动员尽全力进行蹬踏，造成肌肉处于明显的疲劳状态。伴随运动组数的增加和间歇时间的交替，运动员的肌肉疲劳状况也在处于不断的调整变化之中。对该过程中肌肉疲劳状态的监测和评定，对于从理论上深入认识大强度间歇训练中人体运动的神经肌肉控制机制以及从实践层面科学制定和评估运动训练方案都具有重要意义。

表面肌电信号（surface electromyography，sEMG）作为从肌肉表面记录到的时间序列信号，其幅值和频率等信息与肌肉的功能活动密切相关，且具有非损伤性、实时性、多靶点测量等优点，已广泛应用于运动性肌肉疲劳的检测和评估之中（Cifrek et al.，2009；Zawawi et al.，2015）。但是，由于肌肉在不同收缩方式和负荷强度条件所诱发肌肉疲劳机制的差异性，sEMG指标在评价不同运动方式诱发肌肉疲劳时并未表现出完全一致的适用性。王乐军等（2013a）研究发现，在低负荷静态收缩诱发肌肉疲劳过程中，sEMG的均方根振幅RMS表现出优于其他指标的敏感性和稳定性。但在快速点击鼠标和30 s全力蹬踏自行车运动过程中，基于小波包分析计算的平均功率频率指标MNF则表现出良好的适用性（王乐军等，2013b；Wang et al.，2018）。自行车速度型间歇性训练作为一种较新的运动训练方法，目前尚未有针对该训练方式诱发下肢肌肉疲劳的sEMG评价效果进行的研究。

运动性肌肉疲劳可以定义为“运动引起肌肉产生最大收缩力量或最大输出功率暂时性下降的生理现象”（Vollestad，1997）。根据该定义，疲劳后肌肉最大收缩力量或最大输出功率的下降率被认为是定量评价肌肉疲劳程度的客观标准而被广泛采用。在对sEMG指标反映局部肌肉疲劳的效果进行评价时，通过考察研究指标与肌肉最大收缩力量或最大输出功率的同步变化关系，可以为指标的适用性效果做出科学性的评价（Ikemoto et al.，2006；Troiano et al.，2008）。灰色关联度分析作为定量评价分析数据序列与标准序列曲线接近程度的分析方法，可以揭示分析数据序列随标准序列同步变化的一致性程度（Wen，2016；Xu et al.，2014）。因此，sEMG指标与肢体最大收缩力量或最大输出功率的灰色关联度可以作为考察sEMG指标在评价肌肉疲劳适应性方面的有效指标（Wang et al.，2018）。

股直肌作为全力蹬踏自行车运动过程中最主要的参与肌肉之一，在蹬踏力量的输出和不同蹬踏环节的协调转换及力量传递中都发挥重要作用，且是蹬踏自行车运动过程中最容易疲劳的肌肉，其功能状况直接决定了自行车运动的总体表现（王乐军等，2010；O'Bryan et al.，2014）。本研究通过记录自行车速度型间歇性训练过程中右侧股直肌的sEMG，分别计算sEMG的均方根振幅RMS、基于傅里叶变换的中值频率MF和平均功率频率MPF、基于小波包变换的中值频率MDF和平均功率频率MNF、Lempel-Ziv复杂度C（n）、样本熵 SE、基于混沌理论的分形维FD等指标，并基于sEMG各分析指标与输出功率的灰色关联度，对sEMG各指标评价间歇性训练诱发股直肌疲劳的效果进行探讨。

1 研究对象与方法

1.1 研究对象

以10名上海市优秀场地自行车运动员为研究对象，其中男7名，女3名（表1）。受试者皆为接受过5年以上场地自行车专业训练的在役健将级运动员。在实验前告知受试者相关的测试方法、程序及注意事项，并对受试者身体健康状态进行调查，确保受试者在实验前身体健康，在实验前24 h未从事剧烈运动，无肌肉疲劳症状。精神状态良好，无睡眠不足、精神萎靡等不良状态。

1.2 实验程序

在上海市体育科学研究所竞技体育二中心的实验室进行测试，实验室温度设置为24℃。采用Wattbike Pro风阻功率测试车进行自行车蹬踏负荷实验。该功率车具有空气（1～10档）和电磁（1～7档）两套阻力系统。在本研究中，电磁阻力设为1档，空气阻力在不同运动阶段分别设置为不同的档位（详见下文）。

表1 受试者基本情况Table 1 The Basic Information of the Subjects

正式实验前，受试者先在第3级风速档位以90 rpm的蹬踏速度进行5 min热身运动。热身结束后休息10 min，进入正式实验测试。在正式实验中，受试者需要完成5次全力蹬踏自行车运动，每次蹬踏持续时间为6 s。每2次全力蹬踏运动之间，受试者在第1级风速档位以60 rpm的蹬踏速度进行休息调整（图1）。

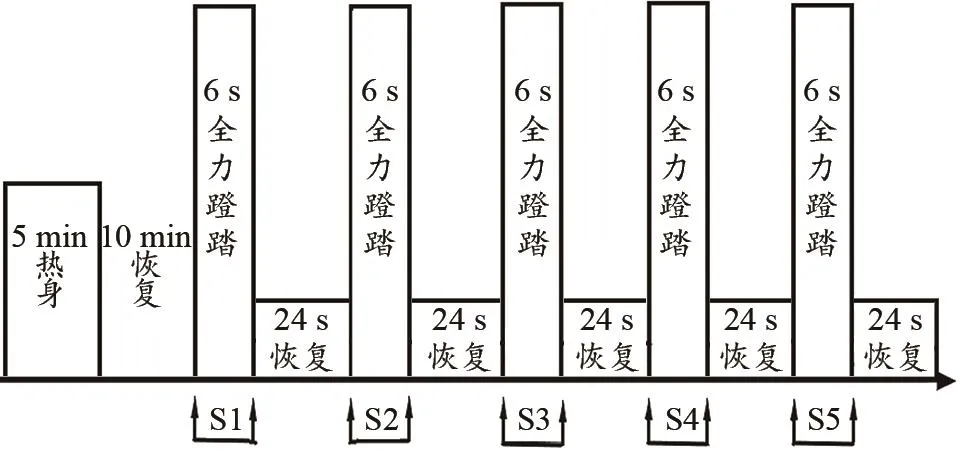
图1 实验方案示意图Figure 1.Experimental Protocol

在6 s全力蹬踏自行车运动中，受试者在功率自行车上尽最大努力进行全力全速蹬踏。每位受试者的风速档位设置为该受试者可以产生最大输出功率所对应的档位。根据这一标准，10名受试者的风速档位分别设置在6～10档之间。根据Wattbike技术文档，6档和10档风速档位在蹬踏速度分别为40 rpm和130 rpm时，输出功率分别为45 W、55 W和785 W、1 045 W。

在正式实验测试过程中，采用Wattbike功率自行车配套的运动参数记录仪（wattbike performance computer，WPC）采集输出功率和蹬踏频率等运动学参数，参数采集的频率为1 Hz。采用ME6000 P8肌电信号记录和分析系统（芬兰Mega公司产品）记录实验过程中受试者右侧股直肌的表面肌电信号（sEMG）。放置电极前首先进行去毛处理，并用磨砂膏打磨皮肤表面以去除角质和表面污垢，之后用75%酒精棉球清理皮肤表面，以减小阻抗。将一对纽扣式肌电测试电极置于测试肌肉的肌腹表面，两电极间距2 cm。电极位置参照Seniam（http：//seniam.org）所建议的测试标准进行贴放，信号采样频率为1 000 Hz。

1.3 数据处理与分析

1.3.1 表面肌电信号预处理

表面肌电信号的预处理包括滤波处理和分段处理2个环节。滤波处理采用四阶巴特沃斯零相位偏移滤波器，对记录的表面肌电信号进行5～500 Hz带通滤波。在表面肌电信号的分段处理环节，分别将5次持续时间为6 s的全力蹬踏自行车运动数据划分为15段等时间间隔的数据（每段数据持续时间为2 s）。

1.3.2 计算表面肌电信号指标

对于每段持续时间为2 s的表面肌电信号，分别基于时域信号计算均方根振幅（RMS），基于傅里叶变换计算中值频率（MF）和平均功率频率（MPF），基于小波包分析计算中值频率（MDF）和平均功率频率（MNF），基于Lempel-Ziv复杂度算法计算复杂度C（n），基于混沌理论计算分形维（Fractal Dimension，FD），基于非线性分析算法计算样本熵（Sample Entropy，SE）。RMS、MF、MPF、MDF和MNF的计算方法参考前期相关文献所采用的方法（Cifrek et al.，2009）。其中，在表面肌电信号的小波包分析中，选择Dauechies（db6）小波基函数进行小波包分解和重构，在此基础上计算中值频率MDF和平均功率频率MNF。根据Kaspar等（1987）设计的复杂度C（n）的算法计算Lempel-Ziv复杂度。分形维的计算参考Boccia等（2016）的研究，基于盒计数算法进行计算。样本熵按照Richman等（2000）所述的方法进行计算。

1.3.3 肌电指标与运动表现指标的灰色关联度分析

采用灰色关联度分析法，对表面肌电信号指标与运动表现指标（输出功率和蹬踏频率）的灰色关联度进行计算，计算步骤：

1）分别以运动表现指标输出功率和蹬踏频率为母序列（Y），以表面肌电信号指标RMS、MF、MPF、MDF、MNF、C（n）、FD和SE为子序列，建立分析数据序列；

2）对各母、子序列分别用每个序列的各原始数据除以该序列的平均值，实现对各序列数据的标准化处理；

3）计算各子序列与母序列在同一时刻的绝对差值，并列出对应数列表；

4）计算关联系数。以上述差值数列表为基础，将相应差值（ΔX'）、最小差值（Δmin）和最大差值（Δmax）代入灰色关联系数计算公式：

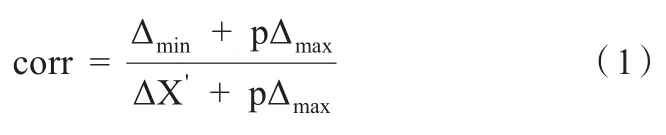
其中，参考相关研究文献，P取0.5。

5）计算灰色关联度。通过将各样本数据计算的灰色关联系数进行平均，即可获得灰色关联度CORR，计算公式为：

其中，n为实验测试的样本点数。

sEMG的处理分析及数据的灰色关联度分析在MATLAB 2016Ra环境下编程实现。

1.4 数据的统计分析

采用KS检验（Kolmogorov-Smirnov test）对各分析数据进行正态性检验。间歇蹬踏阶段和各阶段内蹬踏持续时间与输出功率、蹬踏频率及各肌电指标之间的相关关系采用Spearman等级相关系数进行分析。经过间歇调整后各指标在新阶段内第1个时间点的值相对于上1个运动阶段最后1个时间点值的变化采用配对t检验进行检验。间歇蹬踏阶段和各阶段内蹬踏持续时间对输出功率、蹬踏频率及各肌电指标的影响采用重复测量设计的方差分析进行检验（因变量：输出功率、蹬踏频率及各肌电指标；组内变量1：间歇蹬踏阶段，共5个蹬踏阶段；组内变量2：各阶段内的蹬踏持续时间，分别观察蹬踏持续时间为2 s、4 s、6 s对因变量的影响）。各表面肌电信号指标与输出功率和蹬踏频率的灰色关联度差异采用重复测量设计的方差分析进行检验（因变量：灰色关联度值；组内变量1：各表面肌电信号指标；组内变量2：输出功率vs蹬踏频率）。在主效应显著的情况下，采用Bonferroni多重检验矫正方法确定具有差异的组别。差异的显著性水平为P＜0.05。数据的统计分析工作在SPSS 13.0软件环境下完成。

2 研究结果

2.1 输出功率和蹬踏频率随运动时间的变化特征

5次间歇性自行车蹬踏运动的输出功率和蹬踏频率随运动时间的变化曲线如图2所示。Spearman相关分析结果显示，随着运动阶段的增加，输出功率和蹬踏频率皆表现出显著的单调递减变化（输出功率：r=-0.546，P=0.000；蹬踏频率：r=-0.681，P=0.000）。随着各阶段内的运动持续时间增加，输出功率和蹬踏频率也表现出显著性的单调递减变化规律（输出功率：r=-0.407，P=0.000；蹬踏频率：r=-0.327，P=0.000）。此外，输出功率和蹬踏频率在前1个运动阶段内最后1个2 s内的值分别为836.19±200.44 W和125.13±8.13 rpm，经过间歇调整后在新阶段内第1个2 s内的值分别为977.92±197.90 W和128.78±7.27 rpm。经过间歇调整后，输出功率和蹬踏频率在新阶段内第1个时间点的值相对于上1个运动阶段最后1个时间点值皆出现显著性的增加（输出功率：P=0.000，蹬踏频率：P=0.000）。提示，间歇调整对受试者的输出功率和蹬踏频率皆有显著性的恢复效果。

重复测量设计的方差分析结果显示，间歇蹬踏阶段和各阶段内蹬踏持续时间2个因素对输出功率和蹬踏频率的影响都具有显著的主效应（蹬踏阶段-输出功率：F=51.782，P=0.000；蹬踏持续时间-输出功率：F=71.188，P=0.000；蹬踏阶段-蹬踏频率：F=60.562，P=0.000；蹬踏持续时间-蹬踏频率：F=49.239，P=0.000）。多重比较结果显示，在所有的蹬踏阶段内和各阶段持续时间点上，输出功率和蹬踏频率皆有显著性的差异。间歇蹬踏阶段与各阶段内蹬踏持续时间对输出功率和蹬踏频率的影响皆不具有显著的交互效应（输出功率：F=2.078，P=0.137；蹬踏频率：F=4.290，P=0.068）。

图2 输出功率和蹬踏频率随运动时间的变化曲线Figure 2.The Changing Curve of Power Output and Cycling Cadence with Exercise Time

2.2 表面肌电信号指标随运动时间的变化特征

图3描述了5次间歇性蹬踏运动中各sEMG指标随运动时间的变化曲线。Spearman相关分析结果显示，随着运动阶段的增加，MF、MPF、MDF、MNF、SE、C（n）皆表现出显著的单调递减变化（MF：r=-0.262，P=0.001；MPF：r=-0.289，P=0.000；MDF：r=-0.284，P=0.000；MNF：r=-0.315，P=0.000；C（n）：r=-0.278，P=0.001；SE：r=-0.239，P=0.003），而RMS和FD并没有表现出随运动阶段的显著变化规律（RMS：r=-0.262，P=0.001；FD：r=-0.262，P=0.001）。随着各阶段内的运动持续时间增加，只有RMS和SE表现出显著性的单调递减变化规律（RMS：r=-0.193，P=0.018；SE：r=-0.271，P=0.001），而其他指标随各阶段内的运动持续时间增加并未表现出显著的单调变化规律（MF：r=-0.006，P=0.938；MPF：r=-0.039，P=0.639；MDF：r=0.012，P=0.884；MNF：r=-0.151，P=0.065；C（n）：r=-0.092，P=0.263；FD：r=-0.158，P=0.053）。此外，经过间歇调整后，RMS、MF、MNF、SE、FD在新阶段内第1个时间点的值相对于上1个运动阶段最后1个时间点值皆有显著性的变化（RMS：P=0.002，MF：P=0.048，MNF：P=0.040，SE：P=0.000，FD：P=0.016）。提示，间歇调整对上述5个指标皆有显著的影响作用。

通过重复测量设计的方差分析对间歇蹬踏阶段和阶段内蹬踏持续时间2个因素对sEMG各指标的影响进行检验，发现蹬踏阶段因素对MF、MPF、MDF、MNF、C（n）和SE的影响都具有显著的主效应，其中，在5个蹬踏阶段内，MF在第1阶段和第3～5阶段内的值，MPF在第1阶段和第3～5阶段、第2阶段和第5阶段内的值，MDF在第1阶段和第3阶段、第1阶段和第5阶段、第2阶段和第5阶段内的值，MNF在第1阶段和其他各阶段的值、第5阶段和第1～3阶段内的值，C（n）在第1阶段和第2、3、5阶段内的值，SE在第1阶段和其他各阶段的值皆具有显著性的差异。阶段内的蹬踏持续时间只对MNF和SE表现出显著的主效应，其中，在所观察的3个蹬踏持续时间点上，SE和MNF在第2 s、4 s和6 s的值皆具有显著性的差异。间歇蹬踏阶段和阶段内蹬踏持续时间的交互效应在各sEMG指标上皆未表现出显著性的差异。

2.3 肌电指标与运动表现指标的灰色关联度分析

表面肌电信号各指标与输出功率和蹬踏频率的灰色关联度如表2所示。从表2所列的灰色关联度均值看，在8个表面肌电信号指标中，SE与输出功率和蹬踏频率的灰色关联度最大，分别为0.74±0.05和0.72±0.05；其次为MNF和 MPF，分别为0.68±0.02、0.68±0.05和 0.67±0.04、0.67±0.04；FD与输出功率和蹬踏频率的灰色关联度最小，为0.61±0.06和0.62±0.04。重复测量设计的方差分析结果显示，表面肌电信号指标因素对灰色关联度的影响具有显著的主效应（F=10.658，P=0.000），不同运动表现指标（输出功率vs蹬踏频率）与表面肌电信号指标的灰色关联度无显著性差异（F=1.139，P=0.300），表面肌电指标与运动表现指标的灰色关联度无显著的交互效应（F=0.547，P=0.673）。多重比较结果显示，SE的灰色关联度显著高于其他各表面肌电信号指标（P＜0.05）。此外，FD的灰色关联度显著小于SE和MNF（FD-SE：P=0.000，FDMNF：P=0.04）。

表2 表面肌电信号指标与输出功率和蹬踏频率的灰色关联度Table 2 The Grey Association between sEMG Indices and Power Output and Cycling Cadence

图3 表面肌电信号指标随运动时间的变化曲线Figure 3.The Changing Curve of sEMG Indices with Exercise DurationTime

3 讨论

在本研究中，因男、女受试者人数存在较大差别，需要考虑性别因素对研究结果的影响作用。针对该问题：1）前期研究发现，在5组持续时间为6 s的间歇性全力蹬踏自行车运动中，男、女受试者输出功率随蹬踏时间的下降率并无显著性的差别（Soydan et al.，2018）；2）从 sEMG指标在整个力竭性肌肉收缩过程中的变化率曲线看，基于阵列型电极所测量的动作电位传导速度和分形维数等指标亦未表现出显著的性别差异（Meduri et al.，2016）；3）结合前期对于30 s全力蹬踏自行车过程中输出功率和下肢肌肉sEMG指标灰色关联度研究的受试者性别构成（Wang et al.，2018）可以推测，本研究中男、女受试者人数的差异并不会对研究结果造成显著性的影响。

从受试者的运动表现看，输出功率和蹬踏频率随运动阶段和阶段内蹬踏持续时间的增加都表现出显著性的单调递减变化，提示，随着运动阶段和蹬踏持续时间的增加，受试者下肢肌肉的疲劳程度逐渐加深。此外，经过间歇调整后，输出功率和蹬踏频率会出现一定程度的增加，提示，受试者下肢疲劳程度在经过间歇调整后会产生一定的恢复。基于间歇性蹬踏自行车运动过程中下肢肌肉疲劳程度的变化规律，良好的sEMG评价指标应具备以下特点：1）随运动阶段和阶段内蹬踏持续时间的增加表现出良好的单调性变化；2）经过间歇调整后，所选指标在总体单调变化的基础上能够产生一定程度的恢复；3）在整个运动过程中的变化率曲线与输出功率和蹬踏频率的变化率曲线具有较高的重合度（较大的灰色关联度值）。

RMS作为衡量sEMG幅值的指标，可以反映肌肉运动单位募集数量和激活频率等信息（王乐军等，2013a；Suzuki et al.，2002）。前期研究表明，肌肉在以最大收缩力量或最大输出功率收缩诱发肌肉疲劳过程中，sEMG时域指标随运动时间的延长和疲劳程度的加深而降低（Patikas et al.，2002；Wang et al.，2018）。在本研究中，RMS随阶段内蹬踏持续的增加表现出单调递减的变化，其在间歇调整后也表现出与输出功率和蹬踏频率相一致的变化规律。但其随运动阶段的单调性变化规律并不显著，与输出功率和蹬踏频率的灰色关联度也要低于SE等指标，提示，其在评价由自行车速度型间歇训练诱发股直肌疲劳中具有一定的适用性，但同时也存在不足。在自行车速度型间歇训练过程中，股直肌一直处于较高的负荷运动状态，在该负荷区间内，sEMG幅值随肌肉功能状况变化的敏感性下降（Cifrek et al.，2009；Yassierli et al.，2008）。此外，运动过程中皮肤牵拉和肌肉-皮肤表面电阻的快速变化，也造成RMS具有较大的随机性和波动性，进而影响了RMS在股直肌疲劳评价方面的适用性（王乐军 等，2013b）。

基于傅里叶变换的MF和MPF是评价运动性肌肉疲劳的传统经典指标。研究发现，在静态或动态收缩诱发肌肉疲劳过程中，都伴随sEMG频谱图的左移和MF、MPF的单调性下降。在本研究中，MF和MPF随运动阶段的增加和间歇调整表现出与输出功率和蹬踏频率相一致的变化规律，但其随阶段内运动持续时间的单调性变化规律并不显著，在疲劳评价应用上表现出一定的局限性。由于在自行车速度型间歇训练中，股直肌进行高强度的动态收缩运动，运动过程中皮肤牵拉使检测电极与被检部位肌肉之间的相对位移，加上肌肉收缩过程中长度和厚度不断变化，造成所采集的sEMG具有典型的非稳态、非线性信号的特征（王健等，2005），从而对MF和MPF在疲劳评价方面的适用性产生影响。此外，因傅里叶变换存在时域与频域分辨率的局部化矛盾，为协调实验数据分析的时间和频率分辨率矛盾，本研究中傅里叶变换的频率分辨率为0.5 Hz，也从一定程度上降低了MF和MPF的精确度，并对其在疲劳评价方面的适用性产生影响。

小波包分析被认为是分析非稳定肌电信号较为适宜的方法（王乐军 等，2013b；Sparto et al.，1999；Wang et al.，2018）。前期研究发现，在运动诱发肌肉疲劳过程中，sEMG经小波包变换后的功率谱向低频方向转移，并引起基于小波包分析计算的中值频率MDF和平均功率频率MNF随疲劳程度的加深单调递减（王乐军 等，2009，2013b；Wang et al.，2018）。在本研究中，MDF和 MNF随运动阶段的增加表现出显著的单调递减变化，这与前期研究结果是一致的。此外，MDF和MNF随间歇调整表现出与输出功率和蹬踏频率相一致的变化规律，提示，其在评价自行车速度型间歇训练诱发的股直肌疲劳方面具有一定的适用性。但是，MDF与MNF并未表现出随阶段内运动持续时间的显著单调性变化规律，其与输出功率及蹬踏频率的灰色关联度也显著低于SE，提示，其在评定由自行车速度型间歇训练诱发的股直肌疲劳方面并不是最优的评价指标。

Lempel-Ziv复杂度C（n）是度量sEMG周期性和随机性的指标。前期研究表明，无论是等长还是动态疲劳运动条件下，被检肌肉sEMG的复杂度随着运动负荷时间呈现明显的单调递减型变化（王乐军 等，2013a，2013b）。C（n）随运动时间单调递减的原因，可能跟疲劳程度加深过程中中枢神经系统渐进性协调众多运动单位同步收缩的“协同效应”有关。在本研究中，C（n）随运动阶段的增加单调递减，与前期研究结果是一致的。但是，C（n）并未随阶段内运动持续时间的增加和间歇调整表现出与输出功率和蹬踏频率相一致的变化规律，提示，其在评价由自行车速度型间歇训练诱发的股直肌疲劳方面存在不足。这可能是由于单个运动阶段的运动持续时间仅有6 s，在引起显著外周疲劳的同时，中枢神经系统尚未有效协调股直肌内运动单位以更加同步的方式参与收缩，由此造成阶段内持续时间因素对运动单位同步收缩的“协同效应”影响并不显著。

样本熵SE是从非线性分析角度衡量时间序列复杂性度量信号中产生新模式概率大小的指标，时间序列越复杂，样本熵值越大。在本研究中，SE随运动阶段、运动阶段内的蹬踏持续时间皆表现出显著的单调递减变化，其与输出功率和蹬踏频率的灰色关联度也显著高于其他指标，表明，其在评定自行车速度间歇性训练诱发的股直肌疲劳方面是最优的评价指标。前期研究认为，样本熵可以克服因数据偏差带来的误差，具有更强的抗噪能力和优异的一致性（成娟等，2016）。但当前尚未有研究对sEMG样本熵评价运动性肌肉疲劳的适用性进行过研究。本研究结果揭示了样本熵在提取速度型间歇训练过程中股直肌sEMG疲劳信号特征中的良好应用效果，为局部肌肉疲劳的sEMG评价提供了新的方法选择。

分形维数FD是基于分形理论对复杂形体不规则性的量度，反映了sEMG的自相似结构的复杂程度。在本研究中，FD并未随运动阶段和阶段内的蹬踏持续时间表现出显著的单调性变化规律，其与输出功率和蹬踏频率的灰色关联度也显著低于SE和MNF，表明其在评价自行车速度型间歇训练诱发的股直肌疲劳方面并不具备良好的适用性。前期研究认为，在自行车速度型间歇训练中，下肢肌肉疲劳主要是由外周因素造成的，而与中枢疲劳机制的关系并不密切（Collins et al.，2018）。由于FD仅对中枢性肌肉疲劳具有良好的敏感性，对外周疲劳的变化则不敏感（Mesin et al.，2009），造成本研究中FD在疲劳评价上较差的适用性。

4 结论

在自行车速度型间歇训练中，股直肌进行高强度快速收缩和小负荷间歇调整相结合的运动方式，在造成肌肉产生严重外周疲劳的同时，也使得从股直肌表面记录的sEMG具有非稳态、非线性信号的特征。基于非线性分析计算的样本熵表现出优于其他指标的疲劳评价效果，提示，其在监测由自行车速度型间歇训练诱发的股直肌疲劳方面是可供选择的指标。