低空摄影测量飞机惯导姿态精度评估技术

2019-11-15胡丙华张虎龙张杰

中国测试 2019年5期

胡丙华张虎龙张杰

摘要：针对试飞试验中飞机惯导系统的姿态数据精度评估问题，从航空摄影测量控制定位理论出发，基于POS辅助空中三角测量和光束法区域网平差理论与方法，充分利用各种传感器特性和地面控制条件，实现摄影瞬间飞机惯导系统姿态参数的高精度测量，并与飞机惯导系统实际获取的姿态数据进行残差计算和精度对比分析，进而实现对飞机惯导系统姿态数据精度的评估。飞行试验证明：利用低空摄影测量的密集控制网光束法区域平差方法，能够获取精度高于惯导数据一个等级以上的姿态数据，可充分实现对惯导数据精度的合理评估。

关键词：试飞试验;惯导系统;姿态精度评估;POS辅助空中三角测量;光束法区域网平差

中图分类号：V217.31 文献标志码：A 文章编号：1674-5124（2019）05-0145-06

收稿日期：2018-05-21;收到修改稿日期：2018-09-14

作者简介：胡丙华（1986-），女，湖北赤壁市人，高级工程师，硕士，主要从事摄影测量研究与应用以及光电测试工作。

0 引言

惯性导航系统（inertial navigation system，INS）是一種不依赖于任何外部信息，也不向外部辐射能量的完全自主式导航系统，具有隐蔽性好，提供的导航参数多，抗干扰性强和适用条件宽等优点，因此成为航天、航空和航海等领域中一种广泛使用的主要导航系统[1]。

新型惯性导航系统要在真实飞行环境中才能完成其设计定型/鉴定，进而投入使用。在对INS的位置、姿态角精度的设计定型/鉴定试飞中，曾采用简化过的航空摄影测量方法进行INS位置精度的鉴定，还采用过航空摄影测量中的解析空中三角测量的方法进行惯性导航系统位置、速度和姿态角精度的鉴定，由于解析空中三角测量方法的环节多、技术复杂、工作量大、周期长，特别是要检校出平台式惯导系统的物理平台与摄影影像平面的姿态角误差的技术难度也很大。同时随着INS姿态角测量精度的提高，该法又难于满足其姿态角精度鉴定的要求，因此在后来的INS鉴定的试飞中，采用高精度的INS进行对比试飞[2]。随着全球卫星定位技术的出现和发展，国产INS技术的提高，此时采用国外进口的INS进行对比试飞已不能满足其精度鉴定的要求。目前，INS姿态角测量精度的考核评估则是以地面转台试验为主，即采用高精度的地面转台来评估其姿态角的精度[3-5]。但是，地面试验毕竟不能替代空中真实飞行条件下的飞行试验鉴定，因此本文提出一种新的试飞鉴定方法——基于低空摄影测量的飞机惯导姿态精度评估。该方法通过航摄系统对某测区进行拍摄，获取地面控制场数据、POS数据和航摄影像数据，经数据预处理、影像自动匹配、自由网平差、光束法区域网平差、惯导数据精度分析等处理，实现飞机惯导系统姿态数据的动态精度评估。

1 飞机惯导系统姿态评估方法

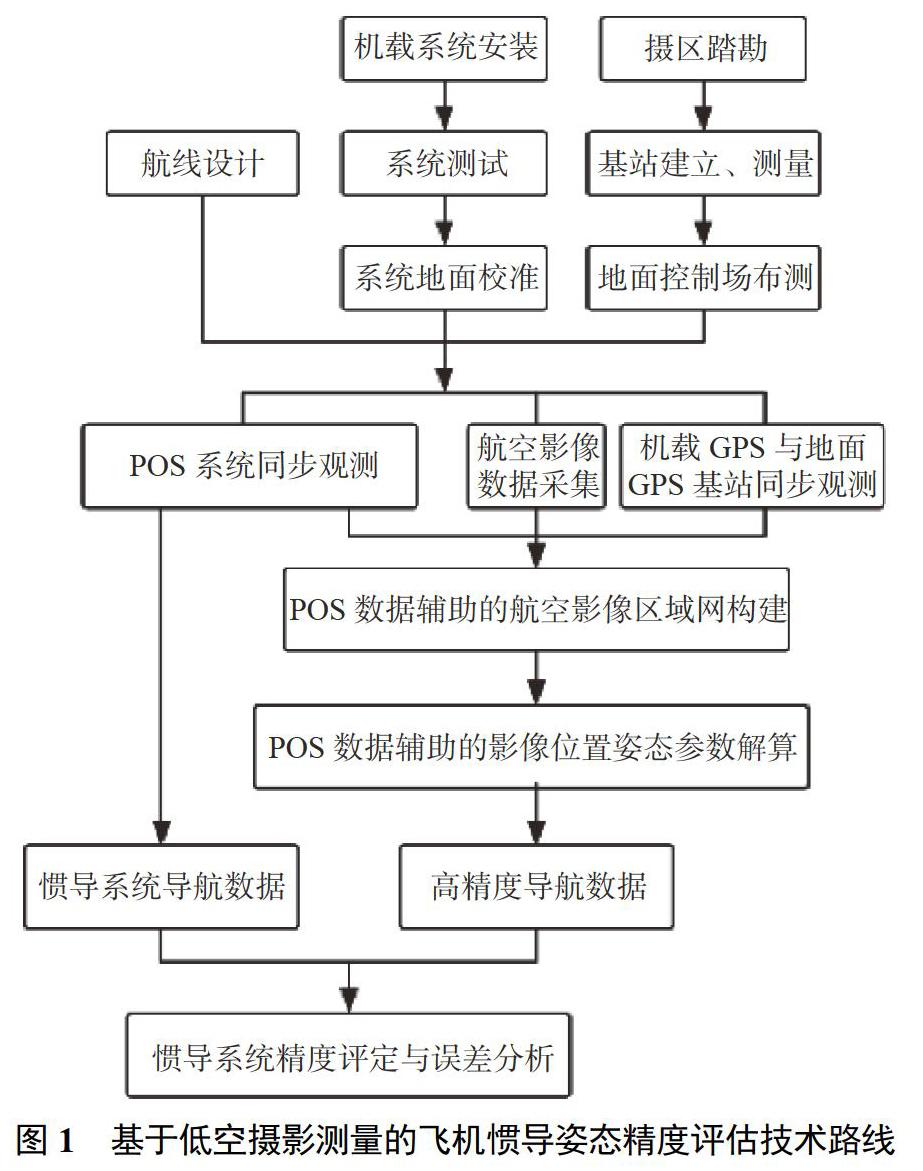
基于低空摄影测量的飞机惯导姿态精度评估方法是在飞行平台上集成高分辨率航测相机、POS系统、被试惯导系统等设备，并在飞行过程中实施对地摄影，利用航空摄影测量领域的相关理论与方法，精确求解出摄影瞬间飞机的姿态航向参数，通过与飞机惯导系统实际获取的姿态数据进行系统分析和比较，科学地评测出民用飞机惯导系统所输出姿态航向数据的实际精度，进而实现惯导系统的精度评估。技术路线如图1所示。其中，为减少评估飞行试验的经费需求，采用地面控制场密集布设与航线高重叠度的设计，结合附加参数的自检校光束法区域网平差技术，实现POS系统辅助的空中三角测量[6]与系统检校工作的同步开展。该方法的核心是POS辅助的航空影像区域网构建、POS辅助的光束法区域网平差和惯导系统姿态精度评估。

1.1 POS辅助的航空影像区域网构建

POS辅助的航空影像区域网构建是将GPS/IMU的观测数据进行严格的联合数据后处理（动态卡尔曼滤波），将其作为航摄相机的空间位置和姿态，以辅助多影像匹配，实现特征点的自动量测和自动转点;利用该数据能有效提高影像匹配的效率、准确性和可靠性。其实现流程如图2所示。

1）GPS/IMU数据预处理

GPS的基本定位原理是卫星不间断地发送自身的星历参数和时间信息，用户接收到这些信息后，经过差分计算求出接收机的三维位置、三维方向、运动速度和时间信息。INS姿态测量主要是利用惯性测量单元（IMU）来感测飞机或其他载体的加速度，经过积分等运算，获取载体的速度和姿态（如位置及旋转角度）等信息。

GPS/IMU数据预处理主要是将原始GPS、IMU数据转换为以航摄相机透视中心为原点的空间坐标系下的位置和姿态数据。预处理结果作为GPS/IMU观测值。

2）影像预处理

影像预处理主要是利用内定向参数对影像进行预处理，即先消除影像的像主点偏移、畸变差，将影像纠正为无畸变的标准影像;然后将彩色影像转为灰度影像，并进行影像增强。

3）特征提取和影像匹配

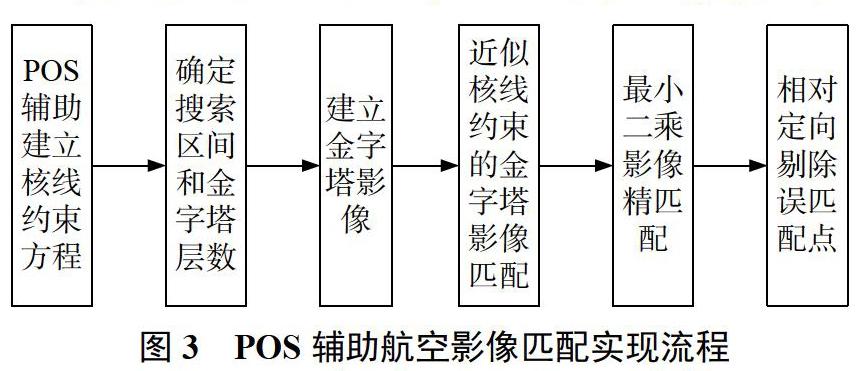
首先采用Harris算子[7]提取出特征点，然后在GPS/IMU导航数据的约束下，采用最小二乘匹配方法实现子像素级别的影像匹配。采用POS辅助影像匹配方法[8-9]自动量测像点，可以大幅提高自动转点中的匹配率和匹配效率，改善某些影像旋角过大、影像纹理不明显、地形起伏较大等难以匹配的影像必须通过手工加点实现转点，进而实现交互量测的难题。同时在匹配过程中引入基于数据探测的粗差分析技术，进行粗差观测值的自动探测和剔除，保证大范围区域影像间精确关系的稳定构建。其中POS辅助航空影像匹配方法的实现路线女口图3所示。

4）自由网平差

自由网平差是利用影像自动匹配获取的连接点进行相对定向，实现摄影区域自由网的构建[10]。相对定向结果精度需达到一个像素以内，以确保影像间连接强度比较稳定，自由网构建结果良好。

1.2 POS辅助的光束法区域网平差

光束法区域网平差是以一幅影像所组成的一束光线作为平差计算的基本单元，以中心投影的共线方程作为平差的基础方程[11]。通过各个光线束在空间的旋转和平移，使模型之间的公共点（亦称连接点）的光线实现最佳的交会，并使整个区域最佳地纳入到已知点的坐标系统中。在具有多余观测的情况下，由于存在像点坐标的量测误差，要使得相邻影像公共点的坐标相等和控制点的加密坐标与地面测量的控制点坐标一致，这就需要采用最小二乘光线束法平差计算，使获得的光线束（影像平面）的外方位角元素和线元素达到最好的精度。具体实现流程如图4所示。

1）光束法区域网平差的基本原理

光束法区域网平差的核心是共线条件方程：

式中：（x，y）、（x₀，y₀）像点和像主点在影像坐标系下的坐标;

f_x、f_y——x，y两个方向的焦距;

P（X，Y，Z）——地面点坐标;

（X_S，Y_S，Z_S）——影像的外方位线元素;

a_i、b_i、c_i（i=1，2，3）——影像的外方位角元素φ、ω、κ所确定的旋转矩阵中的各元素;

（△x，△y）——系统误差改正数;

（X，Y，Z）——中间变量。

2）惯导系统误差改正模型

设机载GPS接收机天线相位中心A在地面坐标系M-XYZ中的坐标为（X_A，Y_A，Z_A），若A点在空间辅助坐标系S-uvw中的坐标为（u，v，w），则利用像片姿态角φ、ω、κ所构成的正交变换矩阵R，可得GPS系统误差改正模型公式+;如下：

式中：a_X、a_Y、a_Z、b_X、b_Y、b_Z——GPS摄站漂移系统误差改正参数;

t₀——参考时刻，其余參数意义同上。

IMU数据与矩阵R满足以下等量关系：

式中：R_I^G（φ'，ω'，κ'）——IMU坐标系到物方空间坐标系的变换矩阵;

R_P^I（△φ'，△ω'，△κ'）——像空间坐标系到IMU坐标系之间的变换矩阵;

φ'、ω'、κ'——IMU获取的姿态参数;

△φ'、△ω'、△κ'——IMU坐标系与像空间辅助坐标系之间的误差[11-12]。

其中，a_φ、a_ω、a_κ、b_φ、b_ω、b_κ为IMU系统误差改正参数，其余参数意义同上。

3）带附加系统误差参数的误差方程构建

以像点坐标、GPS摄站坐标和IMU姿态角为观测值，视物点地面坐标、影像外方位元素以及各种系统误差改正参数为待定参数，依据共线条件方程和POS系统误差改正模型，构建POS辅助光束法区域网平差的误差方程。依照像点坐标、GPS摄站坐标和IMU姿态角的测量精度，分别给予3类观测值不同的权，用最小二乘平差方法求解物点的三维地面坐标和影像外方位元素的最或是值。由于误差方程中考虑了POS系统观测值的累积误差，引入了适当的系统误差补偿模型，可在平差过程中同时解求系统误差改正参数。当平差迭代收敛时，就能自检校并自消除POS系统定位测姿所产生的位置平移和随时间的线性漂移误差，提高了影像外方位元素的测定精度。

4）病态方程求解

当矩阵的条件数很大时，其性态通常较差，直接求逆经常会出现数值不稳定。在很多情况下可以将病态矩阵的求逆问题转化为求解多个相应的病态代数方程问题。矩阵奇异值分解（singular valuedecomposition，SVD）算法可以有效地解决量测方程的病态问题[13]。双边JACOBI算法[14-15]作为广泛应用的奇异值分解算法，可用于上述带附加系统参数的误差方程求解。

5）粗差探测与定位

选权迭代粗差检验的基本思想仍从惯用的最小二乘法开始，但在每次平差以后，根据其残差和其他有关参数，按所选择的权函数计算每个观测值在下步迭代计算中的权值。如果权函数选择得当，且粗差可定位时，则含粗差的观测值的权将愈来愈小。迭代中止时，相应的残差将直接指出粗差的数值，而平差结果将不再受粗差的影响。这样，便实现了粗差的自动定位和改正。根据参与平差的数据特点，选择合适的权函数，经试验验证，采用基于改进丹麦法的选权迭代[16]，能够很好地完成粗差探测与定位，以及剔除处理。

1.3 惯导姿态精度评估

经区域网整体平差后，根据控制点残差统计，计算获得未知数单位权中误差，进而根据协方差阵计算各未知数中误差。当各未知数中误差远小于惯导系统姿态精度时，可将区域网平差获得的姿态数据进行安装偏差量修正后作为真值，与惯导系统导航数据进行对比分析，根据两种方式获得的姿态数据较差分布情况，剔除异常值，再采用均方根误差评价惯导系统姿态精度;当各未知数中误差大于惯导系统姿态精度的1/3时，无法进行惯导系统姿态精度的可靠性评估，需要对试验设计、试验实验与数据处理等环节进行检查和重新规划设计，以实现高精度的空中三角测量处理。

2 试验验证

对西安地区1：1000的404张地面分辨率为0.059701m的UCXP影像进行了空中三角测量处理，影像像素大小为0.006mm。测区分为4条南北飞行、4条东西飞行和1条S型飞行，共计9条航带。空中三角测量处理过程中将南北飞行4条航线单独划分为测区一，将东西飞行及S型飞行航线划分为测区二。对两个测区分别进行影像处理、自动匹配、自由网平差，然后对两个测区数据进行区域网整体平差，平差后根据误差方程残差统计计算各未知数中误差，如表1所示。

由表1比较得出，平差后角元素精度水平高于惯导数据解算精度一个量级，可以将空中三角测量结果作为真值，将两结果之差视为GPS/IMU组合导航数据的误差。在计算出所有航带各曝光时刻不同姿态参数的差值之后，去除明显的错误数据，剩余的姿态误差值可认为满足随机误差分布的规律，用均方根误差来评价其精度。所有航带各曝光时刻不同姿态参数的误差和统计均方根如表2所示。其中Mean是指单航带姿态参数误差的均值;max和min是指单航带姿态参数误差的最大值和最小值，有正负区别;rmsError是指所有误差统计的均方根，无正负区分。

由表2可以看出，IMU在每个航带内姿态误差变化较小，从而评估IMU姿态数据的稳定可靠性;同时可整体评估得出IMU姿态角精度为：航向角0.095°，俯仰角0.014°，横滚角0.016°;与POS系统标称精度：航向0.05°，俯仰与横滚0.008°相比，飞行试验校准得出的精度评估偏低，说明惯导系统经过一段时间的使用，未经过系统误差精确检校，其实际精度很难达到系统标称精度。

3 结束语

基于低空摄影测量的飞机惯导姿态精度评估技术是通过航空摄影测量手段获得更高精度位姿数据来进行惯导系统姿态精度的评估。POS辅助的空三平差系统能对GPS和IMU数据的常量偏移、航带漂移、线性漂移3个系统误差进行有效改正。利用1：1000控制网相对定向-绝对定向结果，结合空三平差系统的精确平差，获取能够高于惯导数据等级的外方位元素数据，达到检校INS系统精度的目的。该方法为我国惯导系统飞行试验动态精度鉴定、评估提供了一种有效技术手段。

参考文献

[1]王文明.基于图像匹配的导航方法研究[D]西安：西北工业大学，2006.

[2]PAYTSAR M，JENNIFER S H，FEIQIN X，et al.GPS/INSnavigation precision and its effect on airborne radiooccultation retrieval accuracy[J].GPS Solutions，2011，15（3）：207-218.

[3]PARAS K，LASKY T A，RAVANI B.Design andimplementation of a mechatronic，all-accelerometer inertialmeasurement unit[J].IEEE/ASME Transactions onMechatronics，2007，12（6）：640-650.

[4]張和杰，李京书.基于双轴转台的捷联惯导系统姿态精度评定算法[J].舰船电子工程，2015，35（4）：51-55.

[5]王浩，刘秀娟，齐建宇.捷联惯导动态角精度实时测试评定技术[J].计算机工程与应用，2017，53（13）：266-270.

[6]邹勇平.POS辅助航空摄影测量应用方法研究与误差分析[D].西安：西安电子科技大学，2010.

[7]张永军.基于序列图像的视觉检测理论与方法[M].武汉：武汉大学出版社，2008.

[8]SUPANNEE T，IMPYEONG L.Using GPS/INS data toenhance image matching for real-time aerial triangulation[J].Computers&Geosciences，2014，72（11）：244-254.

[9]袁修孝，季顺平，昊珍丽.POS辅助航空影像匹配方法：200810246336.0[P].2009-06-24.

[10]张剑清，潘励，王树根.摄影测量学[M].武汉：武汉大学出版社，2003.

[11]杨少文.IMU/DGPS辅助航空摄影新技术在铁路勘测中的应用[J].铁道勘察，2011，37（5）：25-29.

[12]郭大海，昊立新，王建超，等.机载POS系统对地定位方法初探[J].国土资源遥感，2004，16（2）：26-31.

[13]卢波.病态问题的奇异值分解算法与比较[J].测绘信息与工程，2011，36（4）：19-22.

[14]HAN Q，ZENG L.FPGA implementation for low-rankchannel estimation of OFDM[J].Journal of Networks，2012，7（10）：1631-1638.

[15]MA W，KAYE M E，LUKE D M，et al.An FPGA-basedsingular value decomposition processor[C]//Electrical andComputer Engineering，2006.