基于双振速测量面的噪声源定位方法研究
2019-11-15郝振宇郭世旭郑慧峰王月兵杨枭杰
郝振宇 郭世旭 郑慧峰 王月兵 杨枭杰

摘要:在较远距离准确定位噪声源对水下航行器等设备的减振降噪具有重要意义。该文提出一种基于双振速测量面的近场声全息技术,采用双测量面对双噪声源信号的质点振速信息进行提取,利用前后两测量面间的相位差构成格林函数,并根据声场重建公式进行近场声全息声场重建。数值仿真及主峰位置偏差分析表明,基于振速测量的双测量面近场声全息技术,与单振速测量面、双声压测量面的近场声全息技术相比,可以忽略边缘误差的影响,并可以在较远的测量距离更准确的定位声源位置,验证了基于双振速测量面近场声全息技术的有效性和可行性。
关键词:声学;噪声源定位;近场声全息;双测量面
中图分类号:TB95 文献标志码:A 文章编号:1674-5124(2019)05-0140-05
收稿日期:2018-05-21;收到修改稿日期:2018-06-19
基金项目:国家重点研发计划重点专项(2017YFF0206403)
作者简介:郝振宇(1992-),男,河南淮阳市人,硕士研究生,专业方向为仪器仪表工程。
通信作者:郭世旭(1987-),男,河南平頂山市人,讲师,研究方向为水声计量测试技术。
0 引言
水下航行器[1]在反潜战、水雷战、侦察与监视和后勤支援等军事领域起着重要作用,但较大的自身辐射噪声[z]可能会暴露其在布放、攻击过程中的位置信息。准确地对水下航行器的噪声源进行定位是对其辐射噪声特性研究、提高声隐身性和提升攻击命中率的前提,也是利用现代声学诊断进行故障诊断的关键技术[3]。近场声全息技术[4-5]为噪声源识别、定位及声场可视化提供了一种可行的技术手段。国内对近场声全息的研究,大多是以基于空间Fourier变换的方法为主[6];姬庆等[7]通过比较不同格林函数下的噪声源定位精度,得到K-空间抽样格林函数在多噪声源定位时的优势。
为使测量更加方便,需在离噪声源较远的地方进行测量,但随着重建距离的增大,边缘误差也随之增大[8-9],所以常规的单声压测量面近场声全息技术已不满足要求。周东旺等[10]提出一种基于传递函数估计的双声压测量面NAH技术,在近场声全息数据的测量中质点振速比声压更有优势[11-12]。上述方法虽然都可有效进行多噪声源近场声全息重构,但在重构距离较远时,重构误差增大,分辨不出声源的位置。
本文在空间声场变换算法(STSF)的基础上,采用双振速测量面对双噪声源信号的质点振速信息进行测量,利用前后两测量面间的相位差构成格林函数,并根据声场重建公式进行近场声全息声场重建。最后通过仿真研究,把该方法与双声压测量面近场声全息方法、基于单振速测量面的近场声全息方法的处理效果相比较,结果表明该算法在重构距离上有一定的优势,并且体现理论推导的正确性及适用性。
1 基本理论
均匀理想流体介质中的小振幅声波的波动方程为:式中:▽2——Laplace算子;
P(r,t)——声场中任意一点r处的声压;
c——声波传播的速度。
对波动方程进行Fourier变换,得到不依赖于时间变量的Hehnholtz方程:
▽2p(r)+ k2p(r)=0(2)式中:k=ω/c——波数;
ω=2πf——角频率。
定义全息面(测量面)用H表示,重构面(源面)用S表示。
在Dirichlet边界条件下,对于zH>zs的空间为自由场的情况,方程(2)的解为:式中,表示积分在无穷大的平面S上进行。
gDS为Dirichlet边界条件下无穷大平面的Green函数:
gD(xH-xS,yH-yS,zH-zS)=式中,
对方程(4)两边取空间Fourier变换,将空域卷积化为波数域中角谱的乘积:
P(kx,ky,zH)=
PD(kx,ky,zS)GD(kx,ky,zH-zS)(5)
式中:P(kx,ky,zH)——声压p(xH,yH,zH)的空间Fourier变换;
PD(kx,ky,zS)——边界条件PD(xS,yS,zS)的Four-ier变换:
GD(x,ky,zH-zS)——Green函数的空间Fourier变换,解析表达式为
GD(x,ky,zH-zS)=eikz(zH-zS(6)
PN(x,ky)与z=0平面上z向质点振速的空间Fourier变换VZ(kx,ky)之间的关系为:
PN(kx,ky)=VZ(kx,ky)ρck(7)式中,ρ为介质密度。
所以方程(5)可变为:
V(kx,ky,zH)=
VZ(kx,ky,zS)GD(kx,ky,zH-zS)(8)
同样可得反向重构公式:
V(kx,ky,zSx)=V(kx,ky,zH)e-ikz(zH-zS)(9)
由式(9)可得重構面质点振速:
v(xS,yS,zS)=Fx-1Fy-1[V(x,ky,zH)](10)
以上推导为传统的近场声全息理论,本文利用双测量面上相位信息进行近场声全息测量,两个测量面相互平行,两测量面间距为d,d一般不超过λ/10。双测量面近场声全息方法中前后测量面的布置情况如图1所示。
本文中格林函数由前后测量面的数据相位差求得:式中,d为前后测量面之间的距离,Vf、Vr分别为前后测量面的波数域谱。利用以上格林函数会影响所得到的重建面数据的大小,却对重建面数据的相位信息没有影响。
在声场逆向重构时,对波数域噪声信号进行滤波,滤波函数为:式中:kc——空间截止波数;
α——可调参数,表示滤波器阻带上的衰减率。
根据本文所述的双振速测量面声源定位方法,推算步骤如图2所示。
2 双声源定位仿真结果及分析
2.1 单振速测量面法仿真分析
在直角坐标系中,两点声源的中心位于坐标原点,声源频率为800Hz,全息面平行于xoy平面,孔径为12m×1.2m,两点声源坐标分别为(0.3,0.3,0)、(-0.3,-0_3,0),将有限大小的全息面离散成120X120个采样网格,采样点位于网格中心,x和y方向的采样间隔0.01m、0.01m,在实际测量中可使用水听器进行‘弓字形扫描。重构面与全息面平行,面积大小与全息面相等,水中声速c=1500m/s,水密度ρ=1000kg/m3,测量面距离声源表面为ZH,重构面距离声源Zs=0.05m,重构距离为(ZH-ZS)。测量示意图如图3所示。
编程并进行仿真分析,重构面理论振速分布如图4所示。
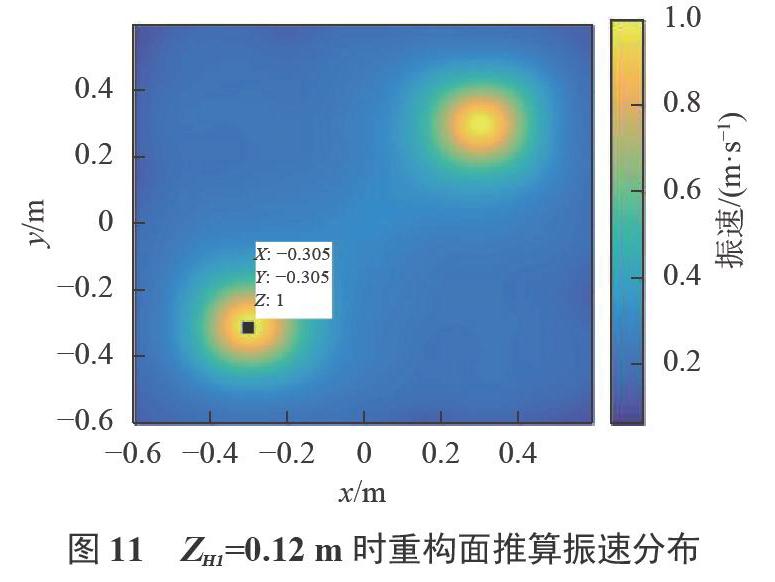
为评价单振速测量面法在不同重构距离处的重构效果,设置不同ZH值进行仿真,分别设置ZH为0.08,0.1,0.12m,在实际测量中,ZH值一般不超过1/3个波长。重构面推算振速分布如图5、图6、图7所示。
由图5可知,当距离较小时,利用单振速测量面法进行近场声全息测量,声源的位置坐标可以清楚识别出来,并且位置也没有偏差;由图6可知,随着重建距离的增大,边缘误差也会逐渐增大,边缘误差的存在会影响声源的位置坐标的识别,逐渐使声源位置模糊,但依旧可以判别声源位置,主峰位置偏差小于5cm;如图7所示,声源位置基本消逝,原因是边缘误差过大,将声源位置信息淹没。所以,利用单振速测量面法进行近场声全息测量时,需要测量传感器与声源很近,随之反射、散射现象严重,距离较大时,伴随有边缘误差,严重限制了近场声全息的应用。
2.2 双振速测量面近场声全息法仿真分析
在进行双测量面近场声全息法仿真分析时,假设条件与常规近场声全息仿真分析假设条件一致。重构面与两个全息面平行,面积大小与两个全息面相等,两个全息面间距为d,两全息面距离活塞声源面分别为ZH1、ZH2,且ZH1
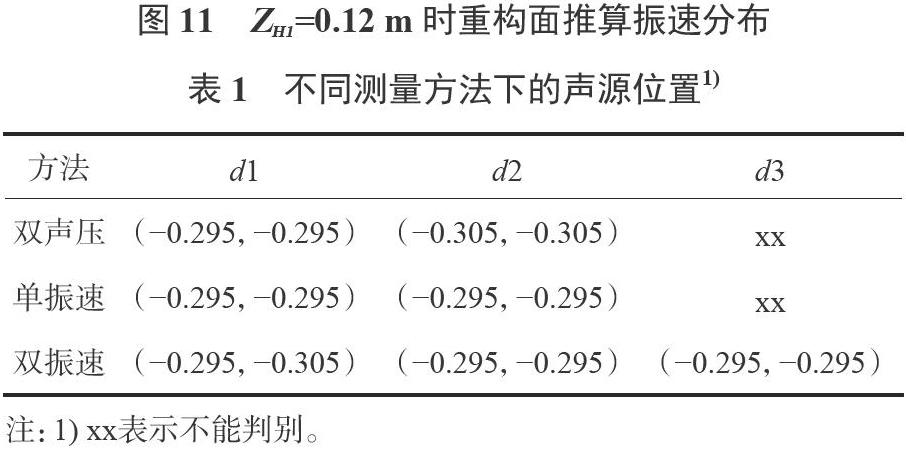
通过比较三种方法得到的负坐标点声源位置可以看出,不论是单振速测量面法、双声压测量面法还是双振速测量面法,在重构距离较小时,都能对双声源进行准重构,完成高精度定位;但随着重建距离的增大,如表1中重构距离为d3时,单振速测量面法、双声压测量面法已经不能判别声源位置,但双振速测量面法仍可以准确找到声源位置,误差为0.005,精度较高,经仿真分析,在本文所设重构条件下,可以分辨声源位置重构距离最大为0.17m,而单振速测量面法、双声压测量面法以分辨声源位置重构距离最大分别为0.07m和0.08m,体现双振速测量面法的优势。虽然双振速测量面法在声源定位是在重构距离方面具有优势,但是在重构振速幅值方面误差较大,不适用于对幅值要求较高的声场推算。与单振速测量面法一样,双振速测量面法在进行近场声全息测量时,频率的增加、重建距离的增大都会使重建误差增大,使重建分辨率降低。
3 結束语
本文利用单振速测量面近场声全息理论和双振速测量面近场声全息理论通过对水下双声源进行逆向定位研究,辨别声场中主峰位置的分布从而完成了对水下声源目标的准确定位,并分析了在不同的重构距离下双振速测量面近场声全息理论的优越性。仿真表明,双振速测量面近场声全息理论逆向定位结果与预测设参数一致,重建精度较高,并且对重构距离适用范围较大,论证了双振速测量面近场声全息理论应用于水下航行体的噪声源定位的可行性。
参考文献
[1]高峰,姬庆,肖大为.基于NAH的水下航行体噪声源定位仿真研究[J].船电技术,2016,36(3):41-44.
[2]孙军平,杨军,林建恒,等.船舶水下辐射噪声信号理论模型及仿真[J].物理学报,2016,65(12):147-156.
[3]姬庆,蒋培,孙玉绘.基于近场声全息的水下航行器噪声源定位方法[J].水下无人系统学报,2015,23(1):20-25.
[4]WILLIAMS E G,MAYNARI)J D.Numerical evaluation ofthe Rayleigh integral for planar radiators using the FFT[J].Journal of the Acoustical Society of America,1982,72(6):2020-2030.
[5]WILLIAMS E G,MAYNARI)JD,SKUDRZYK E.Soundsource reconstructions using a microphone array[J].Journalof the Acoustical Society of America,1980,68(1):340-344.
[6]陈心昭,毕传兴.近场声全息技术及其应用[M].北京:中国科学出版社,2013,6-7.
[7]姬庆,程锦房,肖大为.基于不同格林函数的噪声源定位方法研究[J].压电与声光,2017,39(3):378-382.
[8]刘强,王永生,苏永生.重建参数对平面近场声全息重建精度影响研究[J].武汉理工大学学报(交通科学与工程版),2014(4):811-815.
[9]辛雨.基于空间声场变换的近场声全息参数选取及重建误差研究[D].合肥:合肥工业大学,2009.
[10]周东旺,李舜酩,江星星,等.基于传递函数估计的近场声全息的噪声源识别[J].仪器仪表学报,2015,36(12):2874-2880.
[11]WILLIAMS E G,Ⅲ J AM.FOURIER A Sound radiation andnearfield acoustical holography[J].Journal of the AcousticalSociety ofAmerica,1999,108(4):1373-1375.
[12]JACOBSEN F,LIU Y.Near field acoustic holography withparticle velocity transducersa)[J].Journal of the AcousticalSociety ofAmerica,2005,118(118):3139-3144.
(编辑:徐柳)
