高速列车明线交会流致振动耦合响应分析
2019-11-15周建容陈春俊艾永军李新
周建容 陈春俊 艾永军 李新


摘要:为探究高速列车在流致振动作用下会车压力波对车内气压的影响机理,针对某线路试验高速动车组采用多重等效方法建立有限元车厢、流场以及耦合系统模型,并进行耦合系统模态分析;通过列车交会侧传感器实测会车压力波信号,对车厢耦合系统进行气压冲击加载,分析车内流致振动耦合响应情况;将线路实测车内气压数据运用经验模态分解方法自适应分解,获取各本征模态层,并与流致振动响应数据进行对比分析。结果表明,车体振动位移的频率分布与加载的会车压力波频率相吻合;车内气压级在6.1Hz、14.67Hz处较大,分别与耦合系统的第一阶非刚性模态频率与结构的第一阶模态频率相吻合;同时验证会车压力波在车厢流致振动耦合模型下对车内气压影响机理分析的正确性。
关键词:会车压力波;流致振动耦合;气压冲击;振动响应
中图分类号:U260.16 文献标志码:A 文章编号:1674-5124(2019)05-0134-06
收稿日期:2018-07-19;收到修改稿日期:2018-08-19
基金项目:国家自然科学基金资助项目(51475387)
作者简介:周建容(1993-),女,四川三台县人,硕士研究生,专业方向为振动噪声、空气动力学。
通信作者:陈春俊(1967-),男,四川蒲江县人,教授,博士,研究方向为仪器科学与技术、测控技术、空气动力学等。
0 引言
高速列车内部噪声传播路径包括空气声传播与固体声传播,目前高速列车多为空调列车,密封性较好,故车内噪声主要由固体声传播引起。据研究表明,在低马赫数情况下,脉动压力是气动噪声之源[1],因此研究车外气压通过二次固体传声对车内的影响机理具有重要意义。明线会车是高速列车行驶中较常见的一种工况,高速列车明线交会时,列车与空气挤压形成会车压力波[2],不仅会引起车体的横向振动,而且车厢作为典型的弹性薄壁腔体结构,会车压力波还会引起列车车壁与车厢内流场产生耦合作用,引起车厢内气压变化以及噪声增加。因此研究会车时产生的气压冲击通过车体的流致振动耦合作用对车内气压变化的影响,对探究车内噪声传播机理以及减振降噪具有重要意义。
在弹性薄壁腔体结构的声振效应方面,文献[3]基于汽车声振耦合模型,以车身振动数据为边界条件,获取了车内声学响应。文献[4]建立了装载机驾驶室以及声腔的有限元模型,通过声振耦合模型进行了频率响应分析和降噪设计。目前,声振耦合效应方面的研究主要集中在汽车、装载机、航天、板一腔系统等方面,能运用其进行噪声的预测、低噪声设计以及结构的优化设计,但是在高速列车上基于声振耦合模型研究较少。文献[5]对高速列车车厢结构进行了声振耦合模型的谐响应特性分析,但列车建模简化较多,且主要分析了列车模型的模态特性,对气压加载特性分析较少。高速列车车厢结构复杂,数值分析模型建立困难,为此可利用夹芯板等效的方法建立高速列车车身结构的等效模型,夹芯板等效最初是由Libove等[6]学者对波纹夹芯板进行了研究,后面也有不少学者投入到夹芯板等效的研究中,但是等效方法不统一,等效结果验证较困难,且基本都只考虑了位移变形等效,未进行模态等效,等效模型建立不完整。
以某线路试验高速动车组中间车厢为研究对象,分别对铝合金中空型材的車身与蜂窝板结构的车门建立列车等效模型,基于流致振动耦合有限元方法,分析车厢耦合系统的模态频率特性;通过列车交会侧壁面传感器实测的会车压力波信号,对车厢耦合系统进行气压冲击加载,在流致振动耦合作用下分析车内气压响应情况,研究气压传递规律,为列车室内的噪声研究以及减振降噪提供参考。
1 流致振动耦合分析原理
随着高速列车的提速,车外气动作用加剧,车外流体的激扰将引起列车振动,而高速列车车厢作为弹性薄壁腔体结构,车体的振动又将与车内流场产生耦合作用。在封闭的结构流场中,流场会对结构振动产生影响,此时结构有限元方程[7]为
Mss+Kss=Fs+ATP(1)
式中:Ms、Ks——结构的质量矩阵、刚度矩阵;
Fs——结构所受的外载荷;
s——结构节点的位移向量;
p——流体的相对压强;
A——结构-流场的耦合矩阵。
在考虑结构一流场相互耦合作用时,结构振动也会对室内流场产生影响,此时流场的有限元方程[v]为
Mpp+Kpp+ρpAs=0(2)
式中:Mp、Kp——流场的质量矩阵、刚度矩阵;
ρp——流体介质密度。
求解结构一流场的耦合问题时,需要耦合求解离散后的流场有限元方程和结构有限元方程,为
2 高速列车模型建立
2.1 车身铝合金中空型材等效模型
高速列车车体承载结构是以大型中空铝合金挤压型材焊接而成的双壳结构,可以减小车体质量,并且提高整体刚度性能,但该结构在数值分析中建模困难、计算量大,难以直接求解,故可通过建立等厚度的各向异性板材来等效三角夹芯板的中间夹芯层。
三角夹芯板结构见图1(a),取夹芯层的一斜板单元AB,见图1(b),以推导y方向的弹性常数为例[8],假设等效后的模型在y方向处于均匀拉伸状态,y方向的等效应力在x方向上保持不变,取x方向的一个单元长度分析,若月召板受到力H与弯矩M作用。
由图1受力分析有:
M=Hhc/2,H=σyhc(4)
式中σy为y方向的等效应力,Pa。
可得板AB的弯曲挠度为
δm=Ml2/6EIc=Hl3sinφ/Etc3(5)
式中:E——夹芯板的弹性模量,Pa;
Ic——惯性矩,Ic=tc3/12。
板AB的拉伸长度为
δn=Hlcosφ/Etc(6)
则y方向的变形为
δyH=δmsinφ+δncosφ=Hl/Etc3(hc2+cos2φtc2)(7)
可得y方向的等效弹性模量为
z方向的变形为
δzH=δmcosφ-δnsinφ=Hl/Etc3(l2-tc2)cosφsinφ(9)
则泊松比为
同理,可推导其他等效弹性常数。
根据等效前后质量守恒,等效密度为
ρ=ρctc/psinφ(11)式中PC为原夹芯板的密度,kg/m3。
2.2 车门蜂窝结构等效模型
高速列车的门板为铝合金蜂窝夹层结构,该结构强度高,隔热隔振性能好,但也会导致列车建模、求解困难。通过将蜂窝结构的上下板与中间夹层分开,可将蜂窝夹层结构等效为一均质等厚度的正交异性板[9],从而减少计算量。
蜂窝结构单元见图2(a),以推导x方向的等效弹性常数为例,假设等效后的模型在x方向受到均质拉伸作用,x方向受到的应力为σx,见图2(b),取蜂窝芯单根杆件AB,受力分析见图2(c),其受到力P与弯矩M作用。
由图2受力分析有:式中b为蜂窝芯杆件的厚度,m。
AB杆件弯曲挠度为式中:I——惯性矩,I=1/12bt3;
ES——蜂窝芯的弹性模量,Pa。
杆件AB的伸长量为
则x方向的变形位移为
y方向的变形位移为
则泊松比为
x方向的弹性模量为
同理可推导其他的弹性常数。
根据等效前后质量守恒,等效密度式中PS为原蜂窝芯的密度,kg/m3。
2.3 等效模型验证
2.3.1 车身夹芯板等效模型验证
運用ANSYS有限元软件分别对原三角夹芯板和等效板的变形位移和模态进行求解计算,原夹芯板模型选用壳单元shell63分析,由层合板等效的等效模型采用solidl85和shell63单元分析,两种模型求解得到的变形位移见图3,前4阶模态频率见表1。
图3中原始模型与等效模型最大位移变形分别为0.625mm与0.617mm,相差1.28%,两种模型变形基本一致。表1中两种模型的模态频率最大相差0.47%,模态特性也表现一致,表明建立的车身等效模型正确。
2.3.2 车门蜂窝板等效模型验证
分别运用ANSYS建立蜂窝结构的原始模型与等效模型,位移变形见图4,模态频率见表2。
图4中原始模型与等效模型最大位移分别为0.271m、0.270m,相差0.37%,表2中前4阶模态频率最大相差3.35%,表明蜂窝结构的等效模型与原始模型表现基本一致,可以将该等效模型运用到列车建模中。
2.4 列车流致振动模型
以某线路试验高速动车组中间车厢为研究对象,依次建立车厢结构、流场以及车厢结构一流场耦合系统有限元模型,模型见图5。车厢车体主要由侧墙、车顶、底架、端墙4部分组成,侧墙与车顶以铝合金中空挤压型材为主,侧墙上安装有门、窗,车门结构为铝合金蜂窝结构,车窗为多层复合结构。底架由牵引梁、枕梁、边梁和波纹地板等组成。车体侧墙和车门分别由铝合金中空型材等效模型和铝合金蜂窝结构等效模型建立,端墙结构由铝合金中空型材和梁组成,室内流场介质为空气,采用Fluid30单元,在车体与流场接触面之间建立结构一流场耦合面。
3 列车交会时耦合系统响应分析
3.1 车厢耦合系统模态分析
车厢车体壁面振动与车厢内流场会产生耦合作用,结构振动将引起车厢内流场流动,而流场又反作用于结构,两者相互制约,使得结构振动与车厢噪声被放大或抑制。分别对车厢结构、流场以及结构一流场耦合系统进行模态分析,选取前50阶模态频率进行对比,表3列举了3种模型的部分模态频率,流场的第1阶模态以及耦合系统的前7阶模态均为刚性模态。
3.2 会车压力波加载
高速列车明线交会时,车体与空气之间相互挤压,使列车在车厢表面产生一个移动的压力波,对车体结构与车内的舒适性均会造成很大的影响。选取某线路试验高速列车在300km/h速度级下会车压力波作为车厢流致振动耦合模型气压加载数据。实测气压数据滤除高频干扰及气压基准,以均布载荷的方式加载至列车会车一侧,并在列车底架枕梁上施加固定约束,列车加载数据见图6。
3.3 耦合系统响应分析
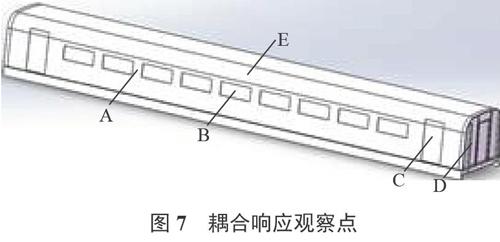
选取车厢内部不同位置测点观察列车的振动特性以及车内压力的变化趋势,测点选取见图7,A点为会车侧壁板上测点,B点为会车侧车窗中点,C点为会车侧车门中点,D点为端墙上测点,E点为车厢中部测点。
不同位置的车身变形随着加载时间变化历程见图8,所选测点中车窗变形最大,车身侧壁测点与车门测点较为接近,端墙上测点变形最小。各测点的位移响应与压力波载荷趋势一致,且频率特征点相吻合。
车身结构振动引起车内气压变化,参见声压级定义,将气压信号从时域转化到频域内表示,气压转化为气压级为
SPL=101g(p/pref)2(20)式中:SPL——气压级,dB;
p——测量压力,Pa;
pref——基准气压,pref=2×10-5Pa。
观察车内气压分布情况,取车窗B的邻近测点、车厢中部测点E作为观测点,所得气压级见图90
从气压级图中可看出,车内气压主要集中在中低频段,其中低频较大,越往高频移动,气压越小;气压级在6.1Hz、14.67Hz频率点处较大,6.1Hz与耦合系统第8阶模态频率相吻合,14.67Hz与车厢结构的第1阶模态频率相吻合,表明车厢内气压响应与耦合系统、车厢结构的固有特性有关。
4 线路试验验证
选取A点侧壁处测点的车内仿真压力与该位置线路实测值进行比较,频谱图见图10,由于实际列车运行时列车空调系统、门窗等部位的泄露等,均会影响车内气压变化,导致车内气压实测频谱比仿真频谱分布更广泛,但仿真值的频谱特征点能与对应的实测频谱一致。
通过经验模态分解方法使实测气压信号依据自身成分特性进行自适应分解,得到各本征模态层,见图11,其频率依次由高向低排列。
利用相关性系数法分析各个本征模态层与仿真压力信号的相关性:式中:xj——实测信号第j个本征模态层数据;
Y——仿真数据;
n——数据长度。
相关性系数r越大,表示两组数据越相关,经过计算,第3层的数据与仿真数据的相关性为0.5633,两组数据关系密切。第3层数据与仿真数据对比见图12,由于实际测试受外界影响因素错综复杂,导致气压响应仿真值比实测值偏小,细节处略有差异但主体趋势一致,因而可认为实测压力信号中包含有仿真信号的成分。同时说明仿真模型基本能反映实际列车的响应特性,表明所建模型的可靠性较高。
5 结束语
本文将多重等效方法运用到高速列车的模型建立上,可以简化列车模型,减小数值模拟计算量,为列车模型的求解提供便利。建立了车厢流致振动耦合模型,分别对车厢、流场以及耦合系统进行了模态分析。以实测会车压力波信号对车厢流致振动耦合模型进行气压冲击加载,观察到车窗位移比车门与车身的变形大,端墙上的变形最小,振动位移频率分布与加载的会车压力波频率相吻合,表明车体的结构振动特性主要與列车加载载荷有关。车内气压级主要集中在低频段,高频段气压级相对较小,气压级在6.1Hz、14.67Hz处较大,分别与耦合系统第一阶非刚性模态频率和结构的第一阶模态频率相吻合,表明车内气压响应特性与耦合系统固有特性及车体结构固有特性有关。以实测车内压力信号与仿真信号进行对比验证,仿真信号频域基本包含在实测信号内,利用经验模态分解方法分解得到实测信号的各个本征模态层,结合相关性系数定义,实测信号第3层数据与仿真信号相关性较高,说明实测压力信号中包含有仿真信号的成分,表明所建车厢流致振动模型能基本反映车厢振动及室内气压特性,建立的模型可靠性较高。
参考文献
[1]王亚南,陈春俊,何洪阳.高速列车脉动压力的大涡模拟及小波分解[J].机械设计与制造,2015(8):86-88.
[2]RICCO P,BARON A,MOLTENI P.Nature of pressure wavesinduced by a high-speed train travelling through a tunnel D].Journal of Wind Engineering and Industrial Aerodynamics,2007,95(8):781-808.
[3]侯献军,郭金,杜松泽,等.基于声模态和板件贡献分析的车身降噪研究[J].汽车技术,2018(5):41-45.
[4]张俊红,李忠鹏,毕凤荣,等.基于板件贡献分析的装载机驾驶室低噪声设计[J].振动.测试与诊断,2016,36(3):568-574.
[5]徐凯,李跃明.高速列车车厢结构声-振耦合响应数值分析[J].计算机辅助工程,2011(3):42-48.
[6]LIBOVE C,BATDORF S.Elastic constants for corrugated-coresandwith plates[R].NASA TN,1951.
[7]袁培佩.乘用车声固耦合有限元模态分析[D].西安:长安大学,2014.
[8]王青伟,赵才其.三角形桁架夹芯层等效弹性常数研究和夹芯板参数优化设计[J].特种结构,2010,27(5):61-66.
[9]富明慧,尹久仁.蜂窝芯层的等效弹性参数[J].力学学报,1999(1):113-118.
(编辑:莫婕)
