基于黏弹性理论的干热岩井筒变形与损伤破坏研究

2019-11-15郤保平李晓雪熊贵明何水鑫成泽鹏

太原理工大学学报 2019年6期

郤保平，李晓雪，王磊，熊贵明，何水鑫，成泽鹏

(1.太原理工大学 a.矿业工程学院，b.原位改性采矿教育部重点实验室，太原 030024； 2.中国石油化工股份有限公司石油工程技术研究院，北京 100101)

地热因其资源量大、热能连续、清洁无污染的特点，被世界各国确定为维系社会可持续发展的绿色能源，在地热资源丰富的国家得到了较好的开发和利用[1]。开发与利用干热岩地热，首先需要解决的问题是深钻施工。高温高压下井筒失稳是干热岩钻井工程中普遍存在的问题，受到各国科研人员和工程技术人员的高度重视。

青海共和盆地干热岩勘探孔的深钻施工表明，高温高压下钻井过程中井壁坍塌、井眼缩颈和地层破裂是造成干热岩钻井无法继续施工的主要原因。出现上述问题的原因在于：高温高压下井筒围岩蠕变变形显著；地质结构复杂，地层内结构面较多；温度变化导致花岗岩力学特性劣化严重。因此，研究干热岩深钻施工过程中高温高压下井筒围岩变形破坏规律，确定干热岩井筒围岩损伤破坏区域，对于干热岩钻井施工与井筒围岩稳定控制具有重要的理论和工程指导意义。

干热岩井筒围岩稳定控制是一个复杂的世界性难题，涉及诸多学科领域，并且涉及的因素非常多，其中包括热学的因素、力学的因素、热学与力学耦合作用以及热-流-固耦合作用等问题，是一个非常庞大而复杂的系统工程问题。国内外学者在高温高压井筒变形破坏与稳定控制方面做了大量的研究工作。文献[1-3]研究了温度对岩石力学的影响，结果表明：在钻井过程中井筒温度的变化会引起井壁围岩产生热应力，岩石的温度变化产生的热应力与井壁围岩原始应力叠加后极有可能导致井壁坍塌失稳。文献[4-5]采用弹塑性的方法建立了合适的力学模型来分析井壁稳定性。郤保平等[6-7]从试验研究和理论分析角度对热力耦合作用下的花岗岩流变模型的本构关系进行了研究，发现岩石内部胶结物和晶粒之间位错和微破裂的形成造成了热力耦合作用下的岩石流变现象，提出了适用于热力耦合作用后花岗岩的流变模型，并通过试验验证了模型的可行性和合理性。刘泉声等[8]研究了花岗岩弹性模量随温度变化的规律，提出了热损伤的概念，在此基础上推导了热损伤演化方程和一维热力耦合弹脆性损伤等本构方程，并分析了损伤能量释放率随温度变化的一系列演化规律。刘成[9]通过分析地应力、孔隙压力、渗透压力以及温度变化的规律，得出了计算井壁围岩综合应力的方程，并运用ABAQUS软件建立了地热井井壁围岩的有限元模型，运用摩尔-库仑准则对古龙井在地层深度6 000 m处的岩石进行了井壁稳定性预测。

本文根据青海共和盆地干热岩勘探孔GR1、GR2揭露的地层构造特征，建立了热力耦合作用下黏弹性数学模型，利用COMSOL软件开展数值试验，探究在深度3 000～4 000 m时，温度、最大水平应力、井径对井筒围岩蠕变变形与损伤破坏的影响规律，以期为干热岩井筒稳定控制提供技术支持。

1 热力耦合作用下井筒围岩黏弹性变形分析理论

1.1 热力耦合作用下岩石黏弹性理论

以主应力形式表示的岩石黏弹性公式为：

σ=σs0+Dεel.

(1)

式中：σs0为初始应力；D为弹性张量；εel为应变量。其中，εel=ε-εeel-εth-εcr；ε为总应变，εeel为弹性应变，εth为热应变，εcr为蠕变应变。

1.2 热力耦合作用下岩石蠕变本构关系

由岩石流变特性可知，岩石在高温高压下蠕变本构方程为：

(2)

式中：σeff为偏应力(MPa)，σeff=σ1-σ3；A为蠕变率系数；Q为蠕变激活能；R=8.314 3 kJ/mol；T为温度，K；σref为参考偏应力，σref=1 MPa；n为偏应力指数。

1.3 干热岩井筒围岩损伤变量

在含结构面井筒变形破坏的热黏弹性分析中，引入有效黏性应变量：

εeve=εel-εeel-εth.

(3)

式中：εeve为有效黏性应变；εel为应变量；εeel为弹性应变；εth为热应变。

1.4 Drucker-Prager强度准则

Drucker-Prager强度准则是在Mohr-Coulomb强度准则和von Mises强度准则的基础上扩展和推广而得。von Mises强度准则适用于以延性破坏为主的岩石。Drucker-Prager强度准则不仅考虑了中间应力的作用，还考虑了静水应力情况，克服了Mohr-Coulomb强度准则的主要弱点。因此，井壁的黏弹性力学模型选用Drucker-Prager强度准则。

Drucker-Prager强度准则的屈服函数计算公式如下：

(4)

式中：I1为第一应力不变量；J2为第二应力偏量不变量；α、K为仅与岩石内摩擦角φ和内聚力c有关的实验常数。

1.5 干热岩井筒围岩蠕变损伤强度准则

将式(3)代入式(1)并整理，得到满足式(4)的基于黏弹性理论的三轴试验条件下干热岩井筒围岩蠕变损伤强度准则表达式：

(5)

2 数值试验

2.1 地质模型

青海共和盆地干热岩钻孔地质结构如下：深度为3 000～4 000 m，以花岗岩、二长花岗岩、黑云母花岗岩为主，并含有大量的结构面，厚度从几厘米到数十米。

基于该特征，结合室内试验结果，将原地层简化为以下三维地质模型，并做出如下假设：

1) 干热岩井筒在地质构造应力的作用下是连续均质、各向同性的；

2) 地层中的流体为单相并且不可以被压缩的理想流体；

3) 花岗岩、结构面和井筒围岩作为一个整体共同承受周围地层的应力；

4) 花岗岩和结构层交界面处清晰可见，胶结较好。

所建立的地质模型如图1所示。结构层位于模型的中部，厚度为50 mm，含有层理、节理或者片理，且裂隙发育。钻井施工将在该地质体上进行。

图1 地质结构模型Fig.1 The model of geologic structure

2.2 物理模型与网格剖分

为了方便与室内试验结果对比，构建了物理模型，如图2所示。模型尺寸为300 mm×300 mm×300 mm，中间含有50 mm厚的结构层，钻孔直径为60 mm.

鉴于物理模型几何尺寸较中间井眼尺寸大得多，且重点研究对象为井壁的变形和位移，采用了疏密网格剖分相结合的方法。井眼处网格剖分精细，远离井眼处网格剖分稀疏，最小单元尺寸1 mm，最大单元生长率1.25，曲率因子0.2，狭窄区域解析度为0.2，而扫掠在裂隙发育段加密。

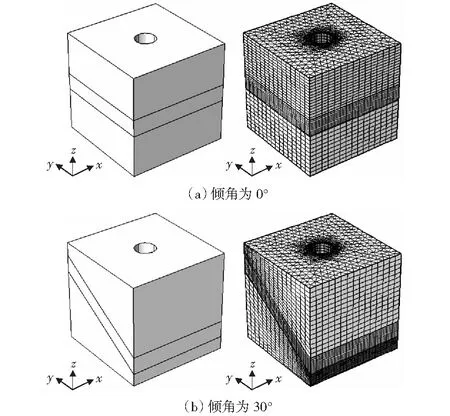
图2 物理模型与相应网格剖分示意图Fig.2 Physical model and schematic diagram of corresponding grid generation

2.3 数值试验设计

影响干热岩井筒围岩变形破坏的因素有很多。本文选取温度、最大水平应力、井径作为变量进行数值模拟试验。模拟计算中求解器选用瞬态研究，瞬态时长为21 600min(15 d).取计算时长为21 600 min时的数据结果进行分析。具体试验设计见表1.

2.4 各岩层物理力学参数选取

根据数值试验设计，对各岩层150～400 ℃温度下物理力学参数进行赋值。根据文献[10-13]中高温高压下花岗岩的物理力学参数进行选取；根据文献[14]中结构层岩石物理力学参数进行赋值，如表2所示。

表1 热力耦合作用下井壁稳定性影响因素及试验设计Table 1 Factors affecting wellbore stability under the action of thermal coupling and scheme design

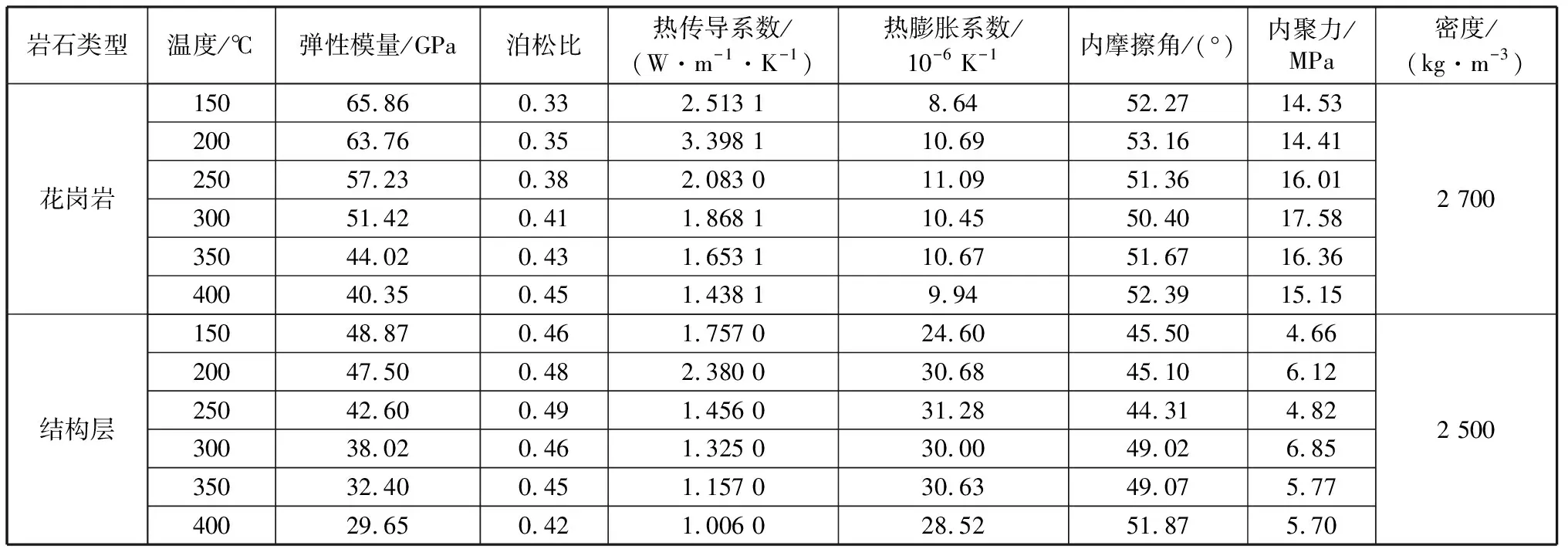
表2 高温高压下各岩层物理力学参数取值Table 2 The physical and mechanical parameters of each rock layer under high temperature and pressure

2.5 边界条件

青海共和盆地干热岩勘探孔施工表明，施工至3 000～4 000 m时，井壁易出现坍塌和缩径现象，无法继续施工。为了能够真实地模拟施工现场边界条件，取应力边界为σv，σH，σh；井筒内温度为20 ℃，干热岩体温度为T.施加的应力边界条件如图3所示，具体赋值见表1.

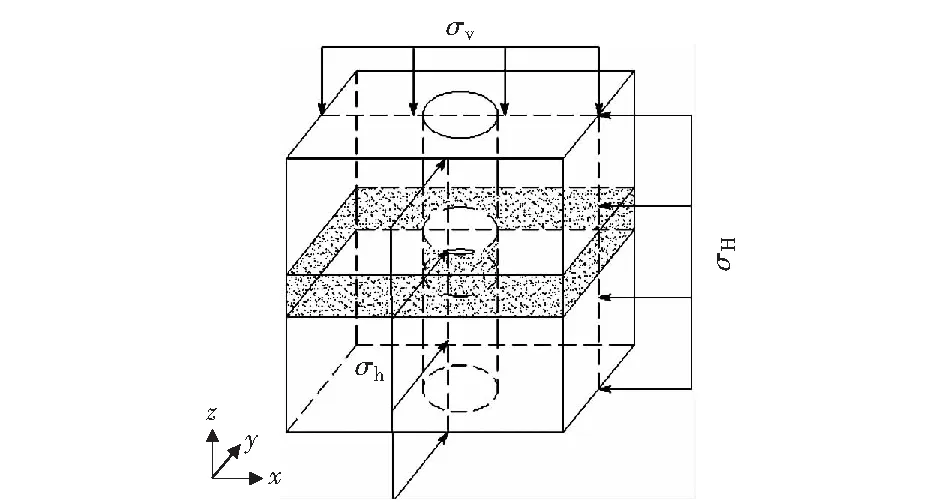
图3 三维物理模型边界条件示意图Fig.3 Schematic diagram of boundary conditions of 3D physical model

3 数值试验结果及分析

3.1 热力耦合作用下含有结构面的井筒围岩变形规律

3.1.1不同影响因素下井壁变形量沿孔深的分布

在图3所示边界条件下，按照数值试验设计进行模拟计算，结果如图4所示。

图4(a)为不同温度下含有结构面的井壁变形曲线。可以看出，在不同温度下井壁变形量沿孔深方向的分布规律相似，且在结构层处变形量均达到最大。孔深在125 mm以内时，花岗岩层中的井壁变形量随着孔深的增加而增加；在结构层内，即孔深为125～175 mm时，井壁变形量达到最大；孔深为175～300 mm时，井壁变形量随着孔深的增加而逐渐减小。温度对于井壁变形量的影响显著，总体上井壁变形量随温度的升高而增大；当温度高于300 ℃时，井壁的变形量明显增大，结构层内的变形更加显著。

图4(b)为不同最大水平应力下的井壁变形曲线，可看出结构层内井壁变形量均高于花岗岩层内井壁变形量。随着最大水平应力的增加，井壁变形量有规律地增加；每增加10 MPa，井壁变形增加量为0.01～0.03 mm.由此可见，应力对于井壁变形量的影响不大，不是造成井壁变形的主要因素。

图4(c)为考虑井径变化对井壁变形影响的数值试验结果，即数值试验三计算结果。由图可知，相同边界条件下，随着井径的增加，井壁变形趋势基本相同，且在结构层内变形量达到最大。随着井径的增加，井壁变形量呈均匀增大趋势。同样，井径也不是造成井壁破坏的主要因素。

综上所述，干热岩地质体内结构面对于井筒变形影响较大；温度对于井壁变形量影响显著，是造成干热岩井筒变形的主要因素。

3.1.2井筒围岩各岩层的蠕变变形

在上述数值试验研究结果的基础上，重点考虑温度影响下井壁围岩中各岩层随时间的蠕变变形量。

图5为不同温度下含结构面井筒各岩层蠕变变形随时间变化曲线。由图可知：相同温度下，结构层内井壁蠕变变形量大于花岗岩层内井壁蠕变变形量；随着温度升高，蠕变变形显著增加，蠕变变形量越大，井壁越容易失稳破坏；井壁蠕变变形随着时间的增加而趋于稳定。蠕变过程只经历了初始蠕变和稳态蠕变两个阶段，一般很难进入加速蠕变阶段。

图5 不同温度下含结构面井筒各岩层蠕变变形-时间关系曲线Fig.5 The curves on creep deformation-time relationship of each rock layer in wellbore with structural face at different temperature

图6为高温高压下花岗岩中钻孔围岩蠕变变形随时间的变化曲线，参见文献[15]。

图6 高温高压下花岗岩中钻孔围岩蠕变应变-时间关系曲线[15]Fig.6 The curve on creep strain-time relationship of borehole in granite under high temperature and high pressure[15]

将图5数值试验结果与图6相比较可知，不同温度下井壁蠕变变形的数值模拟结果与实验结果基本相符。由此可见，所建立的黏弹性模型具有一定的适用性和合理性，数值试验揭示的规律对于工程实践具有重要参考价值。

3.2 不同影响因素下含结构面的井筒围岩损伤破坏规律

为了能够更加明确地表示干热岩井筒围岩损伤破坏区域，我们引入井筒围岩损伤半径和损伤体积比两个概念。其定义如下：损伤半径为井筒围岩损伤最大范围的一点到井眼中轴线的距离；损伤体积比为井筒围岩内已损伤的体积与初始状态体积之比，即

(6)

式中：M为损伤体积比；Vef为井筒围岩内已损伤的体积；V为初始状态体积。

3.2.1不同温度下井筒围岩的损伤破坏

图7为不同温度下含结构面的井筒围岩损伤破坏云图。图8与图7相对应，为相同条件下井筒结构面各岩层损伤破坏随温度变化的曲线。

分析图7，并结合图8给出的每个温度下井筒围岩损伤半径和损伤体积比可知：相同条件下，温度对于含有结构面的井筒围岩的损伤破坏影响显著，300 ℃是一个温度阈值，对于结构层和花岗岩层中井筒围岩的变形破坏影响很大；随着温度的升高，井筒围岩各岩层材料物理力学特性趋于协调，使得井壁变形量增大，但是损伤半径、损伤体积比有所减小。

图7 不同温度下含结构面的井筒围岩损伤破坏云图Fig.7 The cloud map on damage and destruction of wellbore surrounding rock with structural surface at different temperatures

图8 相同条件下井筒各岩层损伤破坏随温度变化曲线Fig.8 The curve on damage of each rock layer of wellbore structure with temperature under the same condition

图8中，温度为150 ℃时，结构层内岩体的损伤体积比小于花岗岩岩层的；随着温度的升高，结构层内的损伤体积比越来越大，300 ℃时损伤体积比达到最大值(3.3%)；此后随着温度的升高，损伤体积比略有减小。而随着温度的升高，花岗岩层内井筒围岩损伤体积比呈现逐渐减小的趋势，从3.0%逐渐减小到1.0%.

3.2.2不同最大水平应力下井筒围岩的损伤破坏

分析图9和图10可知，相同温度和井径下，保持最小水平主应力不变，随着最大水平应力的增加，即两个水平应力比值的增加，结构层和花岗岩岩层内井筒围岩损伤范围基本不变，且结构层内损伤范围始终大于花岗岩层的。此外，随着最大水平应力的增加，结构面和花岗岩损伤体积比均有所减小。由此可见，最大水平应力的变化对含有结构面的干热岩井筒围岩损伤破坏的影响不大。

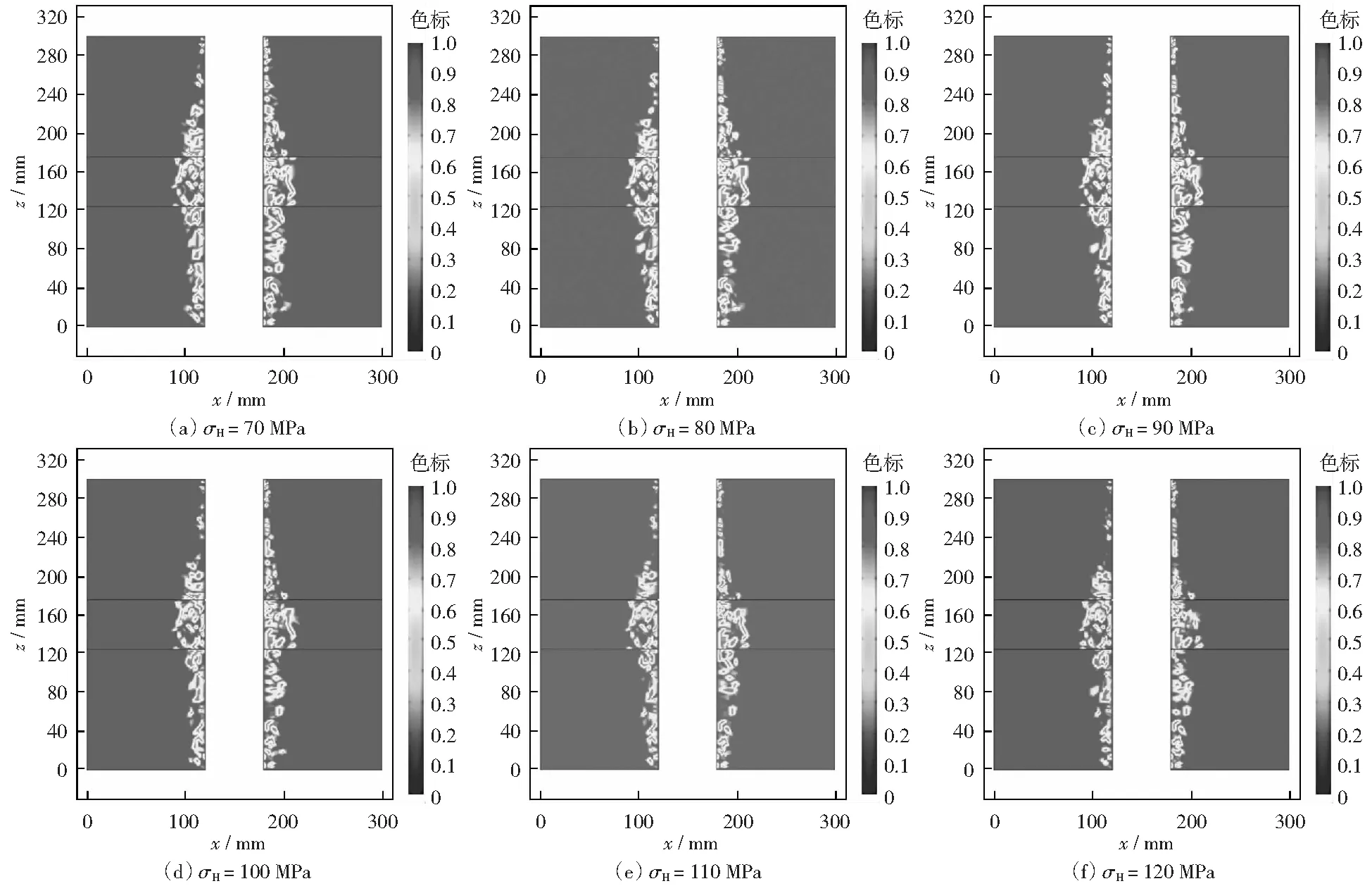
图9 不同最大水平应力下含结构面的井筒围岩损伤破坏云图Fig.9 The cloud map on damage and failure of wellbore surrounding rock with structural plane under different maximum horizontal stress

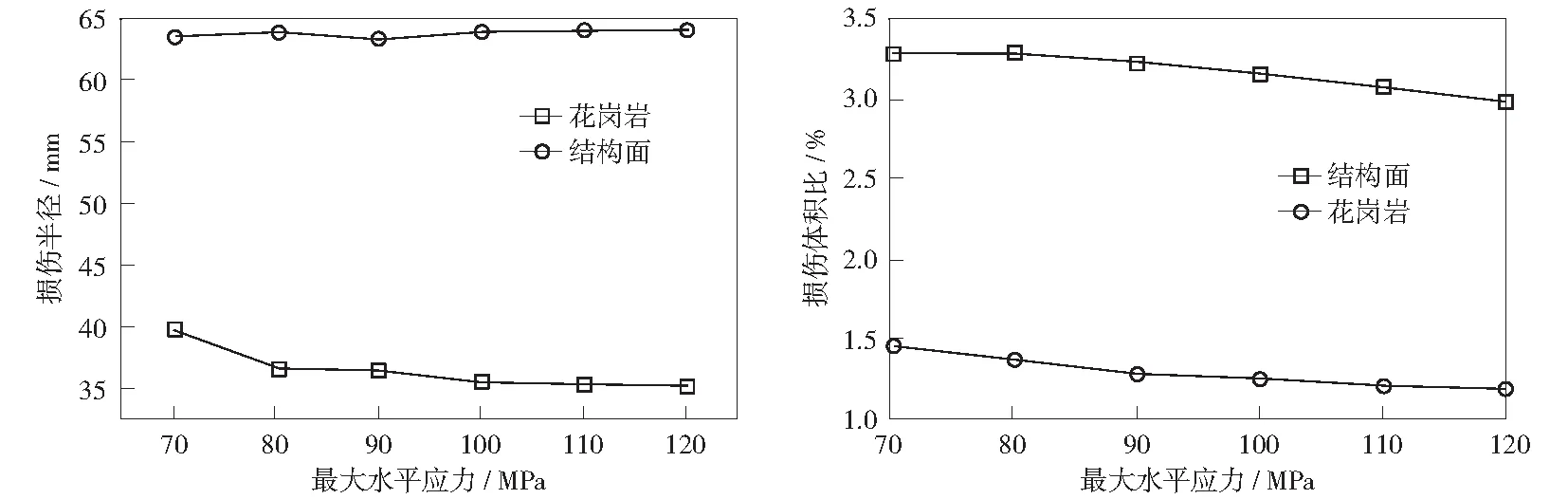
图10 相同条件下井筒各岩层损伤破坏随最大水平应力变化曲线Fig.10 The curve on damage of each rock layer of wellbore structure with maximum horizontal stresses under the same condition

3.2.3不同井径下井筒围岩的损伤破坏

图11和图12为相同计算条件下，不同井径时含有结构面的干热岩井筒围岩损伤破坏云图、损伤半径和损伤体积比。由图可知，结构层内井筒围岩的损伤范围始终大于花岗岩层的；随着井径的增加，花岗岩层和结构层内井筒围岩损伤半径不断增加，且结构层内井筒围岩损伤半径增加得更快；井筒围岩损伤体积比均随着井径的增加而增加。井径在40～90 mm的变化过程中，花岗岩层内井筒围岩损伤体积比呈线性增加；而结构层内井筒围岩在井径为80 mm时损伤体积比开始趋于稳定，且结构层内损伤比约为花岗岩层内的2倍。由此可见，井径是影响井筒围岩损伤破坏的另一个重要因素。

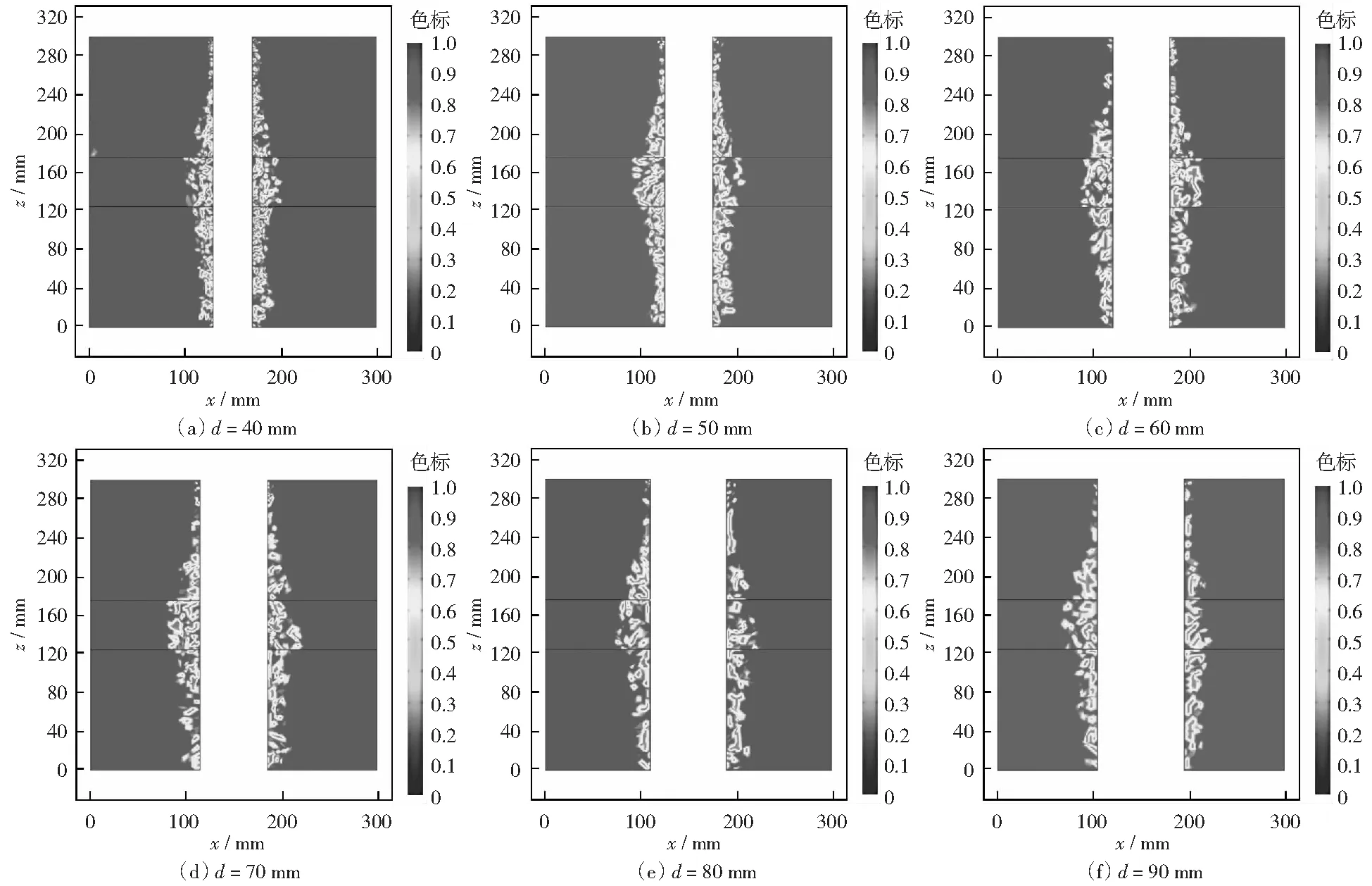
图11 不同井径下含结构面的井筒围岩损伤破坏云图Fig.11 The cloud map on damage and failure of wellbore surrounding rock with structural plane under different wellbore diameter