锥形下行床内流动行为的CFD数值模拟
2019-11-15连文豪潘雪儿杨景轩张忠林郝晓刚
连文豪,潘雪儿,杨景轩,张忠林,郝晓刚
(太原理工大学 化学化工学院,太原 030024)
近年来,随着优质煤炭资源的日渐减少,对褐煤等劣质煤种的利用日益受到重视[1-2]。为实现褐煤资源的清洁、高效利用,日本东京大学提出了三塔式循环流化床反应系统(triple-bed circulating fluidized bed,TBCFB)[3-5]。该系统主要包含燃烧器、热解器、气化器等三个反应单元。鉴于热解反应速度较快,且产物易发生二次反应,选择下行床作为热解反应器。然而,下行床内气、固并流顺重力场流动,带来固含率较低的缺点[6];这不利于相间的快速换热,进而影响了反应效率。因此,如何提高床层固含率是目前该领域的焦点问题。
为提高下行床内固含率,主流思路有两种,即降低气速和提高通量。然而,大量研究表明,采用低气速、零气速甚至逆流等方式都无法显著提高床层固含率,固含率仍保持在10-2数量级[7-8]。因此,研究者们寄希望于通过提高颗粒通量以实现增浓。日本东京大学在TBCFB系统内引入气封床以改善系统内颗粒流动情况,将颗粒循环通量提高到439 kg·m-2·s-1,并获得2.1%的固含率[9]。李志强等[10]设计了一个提升管-下行床-提升管耦合系统,通过提高二级进风量以及颗粒储量,将循环通量提高到400 kg·m-2·s-1,并得到5.5%的固含率。相比于上述通过优化系统压力分布以提高通量的方式,更常见的方式是改进进料器结构。刘卫东等[11]设计了一个带有漏斗状进料结构的下行床反应器;在该进料器的辅助下,颗粒循环通量达到400~1 500 kg·m-2·s-1,相应地获得了高达10%~20%的固含率。与之类似,陈恒志等[12]在一个带有漏斗状进料结构的下行床中进行了实验,实现了高达600 kg·m-2·s-1的颗粒循环通量,同时获得了14%的固含率。参考该类进料器结构,本课题组提出将圆柱形下行床出口收窄,改进为锥形下行床,结果表明该床型确实可以在一定程度上提高固含率[13]。然而,前期工作仅考察了反应器结构、操作气速等因素的影响,没有考虑颗粒通量、密度和粒径等因素的影响。本文通过CFD数值模拟,详细考察了颗粒通量、密度和粒径等因素对锥形下行床内流动行为的影响,以期为锥形下行床的推广及优化提供一些定性指导。
1 模拟方法及验证
1.1 几何模型
为便于比较,本研究选择与前期工作相同的反应器结构[13],如图1所示。图1中,传统圆柱形下行床为参照反应器。

图1 4种不同结构的下行床示意图(单位:m)Fig.1 Schematic diagram of the four downers with different outlet diameter
1.2 CFD模型
综合考虑模拟计算效率与精度要求,选择双流体模型(two fluid model,TFM)作为基础模型。通过耦合颗粒动力学理论(kinetic theory of granular flow,KTGF)封闭颗粒拟流体化后引入的压力相与剪应力相,同时引入k-ε双方程湍流模型考虑气相的湍流行为。
采用商用流体力学软件FLUENT 15.0进行数值模拟。为便于计算,所有结构均简化为2D网格。在正式模拟计算之前,对模型及相关经验参数都进行了详细考察,以确保计算结果的合理[13]。模拟所用参数见表1.通过网格无关性考察,网格总数取值为122 500.

表1 模拟参数表Table 1 Simulation model parameters
文献[13]已经证实该模型的模拟结果准确可靠。鉴于本文使用的是相同的模型,这里不再重复讨论。
2 结果与讨论
2.1 径向固含率的分布
2.1.1颗粒通量对径向固含率分布的影响
为与本课题组之前工作保持一致,本研究同样选取下行床出口位置处径向固含率的分布进行比较。结果如图2所示。

vg=6.1 m·s-1,ρs=1 545 kg·m-3,ds=54 μm图2 不同颗粒通量下径向固含率的分布Fig.2 Radial solids holdup distribution with different solids flux
图2中,出口直径为0.14 m的反应器是作为参照反应器的传统圆柱形下行床反应器。图2清晰地捕捉到了圆柱形下行床中的浓相环形区现象,定性验证了模型的准确性。此外还可发现,锥形下行床中同样存在浓相环形区,且比圆柱形下行床更加明显。原因是锥形下行床沿流动方向截面逐渐缩小,使得颗粒与壁面的碰撞频率显著增加,强化了颗粒的横向迁移;更多的颗粒向浓相环形区移动,使得锥形下行床中浓相环形区更加显著。
对比图2(a)和(b)可以发现,当颗粒通量较高时,所有床型的固含率均显著提高;这与传统下行床的结论一致[14],即提高颗粒通量有助于固含率的提高。原因可能是,较高的颗粒通量意味着单位时间内有更多的颗粒进入反应器。固含率是颗粒相在反应器中的体积分数。因此,当其他操作条件一定时,固含率随颗粒循环通量的增加而增加。
图2(a)中,当颗粒通量为151 kg·m-2·s-1时,随反应器出口直径的减小,浓环峰值呈先显著增大再减小的趋势,最大值出现在出口直径为0.07 m的锥形下行床中。原因是缩小出口直径会同时增大气速和颗粒通量;前者会降低固含率,后者会提高固含率。当反应器出口直径轻微缩小时,气速沿轴向变化不明显,但颗粒与壁面相互作用显著增强,因而浓环峰值增大;进一步缩小出口直径时,气速显著增大并转变为控制因素,因而浓环峰值降低。图2(b)中,当颗粒通量增加到400 kg·m-2·s-1时,随着出口直径的减小,浓环峰值始终保持逐渐增加的趋势。这种反差是由于当气速不变时,增加颗粒通量相当于强化了颗粒通量对固含率的影响程度,间接弱化了气速的作用,使得气速更难转变为控制因素。浓环峰值的最大值出现在出口直径为0.02 m的锥形下行床中,意味着当出口直径缩小到0.02 m时,气速才刚转变为控制因素,或甚至还未转变为控制因素。该现象在一定程度上也体现了自然界中广泛存在的竞争与协调作用机制。
2.1.2颗粒密度对径向固含率分布的影响
图3与图2(a)除颗粒密度ρs不同外,其他操作条件均相同。对比两幅图可以发现,当颗粒密度较高时,所有床型固含率均显著降低,这与传统下行床情形下所得结论一致,即较高的颗粒密度不利于固含率的提高[14]。较高的颗粒密度会带来两方面影响:一是单位时间进入反应器的颗粒数量减少;二是单个颗粒的质量更大,颗粒可以达到更高的速度。以上两个因素均会导致固含率降低。

Gs=151 kg·m-2·s-1,vg=6.1 m·s-1,ρs=800 kg·m-3,ds=54 μm图3 颗粒密度对径向固含率分布的影响Fig.3 Effect of particle density on radial solids holdup distribution
进一步分析发现:当颗粒密度为800 kg·m-3时,气速在出口直径缩小至0.02~0.04 m时才转变为控制因素;而当颗粒密度为1 545 kg·m-3时,气速在出口直径缩小到0.07 m时就已转变为控制因素。在相同颗粒通量时,图3条件下进入反应器的颗粒数量要显著高于图2(a)中的颗粒数量,强化了颗粒密度对固含率的影响程度,间接使得气速更难转变为控制因素。
2.1.3粒径对径向固含率分布的影响
图4与图2(a)除粒径ds不同外,其他操作条件均相同。对比两幅图可以发现,随着粒径的增加,所有床型浓相环形区出峰位置均向中心偏移。这是由于在相同颗粒密度下,较大的颗粒具有更大的质量,因而惯性更大,与壁面碰撞后相应地可以横向迁移更远,导致浓相环形区出峰位置更靠近中心。此外还可发现,较大的粒径会导致固含率的轻微降低,原因是较大的颗粒由于质量较大可以达到更高的速度,导致固含率降低。
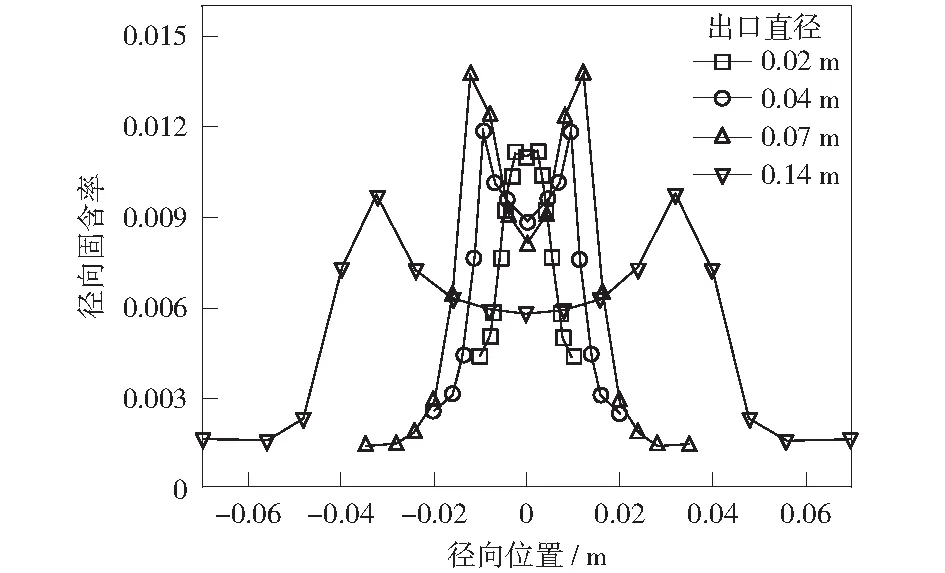
Gs=151 kg·m-2·s-1,vg=6.1 m·s-1,ρs=1 545 kg·m-3,ds=128 μm图4 粒径对径向固含率分布的影响Fig.4 Effect of particle size on radial solids holdup distribution
2.2 轴向流动规律
2.2.1颗粒通量对轴向压力分布的影响
图5(a)和5(b)分别是在颗粒通量Gs为100 kg·m-2·s-1和400 kg·m-2·s-1条件下获得的轴向压力分布图。图5(a)和5(b)中圆柱形下行床的轴向压力分布与文献结论一致,清晰地给出了先下降后上升最后斜率保持不变的趋势,依次对应于第一加速段、第二加速段和充分发展段[15]。由之前工作可知,锥形下行床中压力轴向分布发生了显著变化,呈先下降后上升再下降的趋势,依次对应于第一加速段、第二加速段和第三加速段。详细讨论请参阅文献[13]。
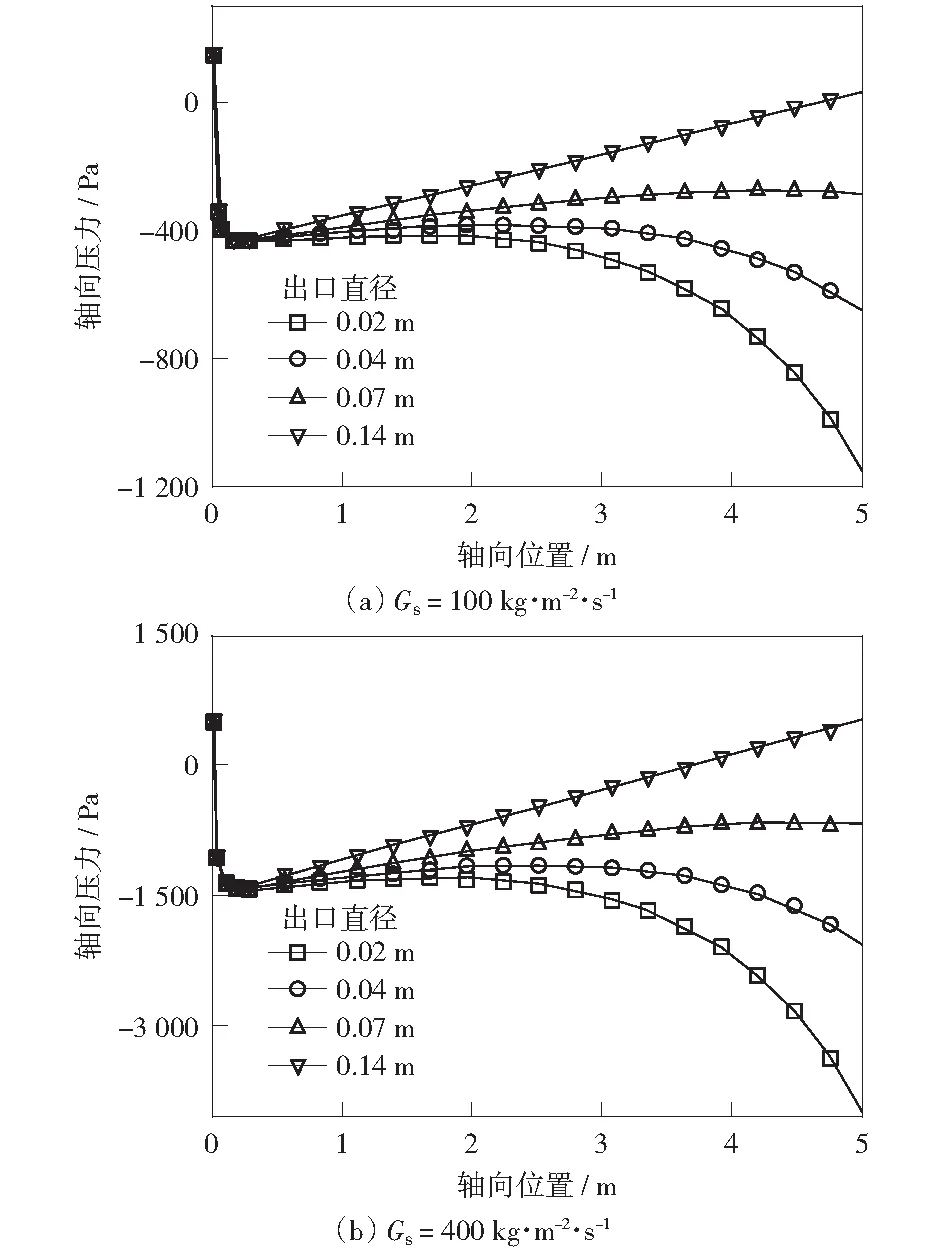
vg=6.1 m·s-1,ρs=1 545 kg·m-3,ds=54 μm轴向位置以进口为基准,以下同图5 不同颗粒通量下轴向压力的分布Fig.5 Axial pressure distribution with different solids flux
图5中,增大颗粒循环通量几乎不会影响圆柱形下行床和锥形下行床中各个流动阶段的长度,原因与下行床内床层固含率较低有关。由图2可知,虽然颗粒循环通量从151 kg·m-2·s-1提升到400 kg·m-2·s-1时固含率提升了约2倍,但由于固含率基数较小,即使提升2倍之后,实际固含率仍然不高(<5%);较低的固含率并不会明显影响反应器内的颗粒流动行为。在这种情况下,两类下行床中各个流动阶段间的临界点,即零压力梯度点以及颗粒力平衡点主要由气速以及颗粒性质共同决定,而与颗粒通量关系较小,故颗粒循环通量几乎没有影响各个流动阶段的长度。
此外还发现,增大颗粒循环通量会使每个流动阶段的压力变化幅度更大;这可由能量守恒定律解释。对于4个下行床反应器,无论处于哪个阶段,必然存在着气相与颗粒相之间的能量交换:较低速度的颗粒可以从气相获取部分能量用于加速,较高速度的颗粒也可以将自身的势能传递给气相。当颗粒循环通量较高时,意味着反应器内颗粒负载较大,此时气固间能量交换势必更加剧烈,导致反应器内产生更为显著的压力变化;而当颗粒循环通量较低时,气固之间的能量交换较弱,压力变化较为平缓。
2.2.2颗粒密度对轴向压力分布的影响
图6是在不同颗粒密度下得到的轴向压力分布图。由图可知,增大颗粒密度会使零压力梯度点下移,即第一加速段变长,原因是密度较大的颗粒由于较大的惯性需要更长的距离完成加速。除此之外,图6(a)和6(b)之间的差别很小。实际上,不同颗粒粒径下得到的轴向压力分布亦是如此。这可由2.2.1部分讨论内容解释,即反应器内压力变化幅度主要由颗粒循环通量以及操作气速决定。为了更清晰地表达颗粒密度及粒径对轴向流动规律的影响,本文接下来重点对轴向气固速度分布进行了考察。

Gs=151 kg·m-2·s-1,vg=6.1 m·s-1,ds=54 μm图6 不同颗粒密度下轴向压力的分布Fig.6 Axial pressure distribution with different particle density
2.2.3颗粒密度对轴向气固速度分布的影响
图7是在不同颗粒密度下得到的轴向气固速度分布图。由图可知,密度较低的颗粒跟随性较好,在整个流场中气固间滑移速度(即气固速度差)都较小。而对于密度较大的颗粒,其滑移速度在大部分轴向位置处均较大;原因是密度较大的颗粒惯性较大,需要较大的滑移速度才能有效推动颗粒。此外还可发现,在圆柱形下行床中,当颗粒密度较大时,颗粒充分发展后的滑移速度较大;原因是密度较大的颗粒重力更大,需要较大的滑移速度才能产生足够的曳力以平衡重力。

Gs=151 kg·m-2·s-1,vg=6.1 m·s-1,ds=54 μm图7 不同颗粒密度下轴向气、固速度的分布Fig.7 Axial gas and solids real velocity distribution with different particle density
2.2.4粒径对轴向气固速度分布的影响
图8是在不同粒径下得到的轴向气固速度分布图。图7(c)除粒径不同外,其他操作条件均与图8相同。对比图7(c)、8(a)和8(b)可以获得与2.2.3部分类似的规律,即粒径较小的颗粒跟随性较好,而粒径较大的颗粒在大部分轴向位置处其滑移速度均较大;原因与2.2.3部分类似,即较大的颗粒具有较大的惯性,需要较大的滑移速度才能有效推动颗粒运动。还可发现,当粒径较大时,圆柱形下行床中平衡时滑移速度较大,原因同上。

Gs=151 kg·m-2·s-1,vg=6.1 m·s-1,ρs=2 600 kg·m-3图8 不同粒径下轴向气、固真实速度分布Fig.8 Axial gas and solids real velocity distribution with different particle size
2.3 锥形下行床对增浓的影响
在之前工作中,通过固定气速考察了锥形下行床对固含率的影响,发现锥形下行床对固含率的提升幅度有限,如图9中黑线与红线所示。实际上,从反应角度讲,更合理的比较基准应为相同停留时间,即tg相同。以褐煤热解为例,当褐煤粒径固定时,若外界固含率没有发生极为显著的变化,其所需反应时间应基本保持不变。若在锥形下行床中使用相同气速,势必显著降低褐煤颗粒停留时间,导致反应不充分。基于此,本工作以相同停留时间为基准,重新考察了锥形下行床对固含率的影响。
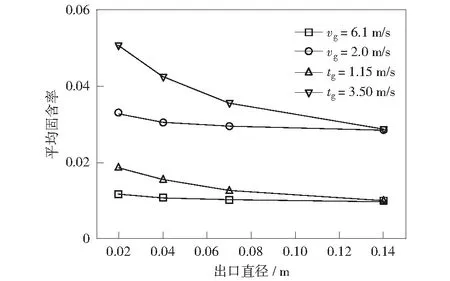
Gs=151 kg·m-2·s-1,ρs=1 545 kg·m-3,ds=54 μm图9 不同比较基准下锥形下行床对固含率的影响Fig.9 Effect of conical downers on the solids holdup under different comparison base
由图9中蓝线和粉线可知,在相同停留时间下,锥形下行床可显著提高床层平均固含率,进而提高相间换热效率及反应效率。这进一步体现了锥形下行床作为褐煤热解反应器的优越性。
2.4 锥形下行床与圆柱形下行床的比较
锥形下行床与圆柱形下行床流型均为气固并流顺重力场流动,因此均适用于反应迅速且目标产物为中间产物的快速反应。结合两者各自特点,它们的潜在应用场景可进一步细分为:圆柱形下行床适用于气相作为反应物的快速反应,而锥形下行床适用于颗粒相作为反应物的快速反应。若气相为反应物,使用锥形下行床势必缩短气相停留时间,导致反应不够充分;若要维持足够反应时间,必然要求降低入口气速,这意味着降低了反应器的处理能力。所以,锥形下行床不适用于气相作为反应物的快速反应,而使用圆柱形下行床不存在该问题。若固相为反应物,使用圆柱形下行床存在固含率低的缺点;而使用锥形下行床一方面可以显著提高床层固含率,另一方面为了维持足够的反应时间需要降低操作气速,一定程度上可以节约载气的消耗。同时,更少的载气消耗意味着载气对生成的气态产物的稀释更少,后续分离成本更低。因此,锥形下行床更适用于颗粒相作为反应物的快速反应。
3 结论
本文采用CFD数值模拟方法系统考察了颗粒循环通量、颗粒密度、粒径等因素对锥形下行床中径向和轴向流动规律的影响,得出如下结论:
1) 增加颗粒循环通量或降低颗粒密度均可显著提高床层固含率,强化颗粒流对浓相环形区峰值的影响,使气速更难以转变为控制因素。
2) 改变颗粒粒径主要影响浓相环形区出峰位置,对固含率影响相对较弱。
3) 改变颗粒循环通量会显著影响反应器内轴向压力变化幅度,而改变颗粒密度、粒径对轴向压力变化幅度影响较弱。
4) 降低颗粒密度和粒径有助于降低气固间滑移速度,缩短第一加速段长度,有效提高颗粒的跟随性。
5) 锥形下行床可以显著提高床层平均固含率,更适合于颗粒相作为反应物的快速反应;而圆柱形下行床更适合于气相作为反应物的快速反应。
需要说明的是,本文的研究工作是基于冷态条件展开的,相关热态研究仍有必要进行。
