基于时变T-Copula 模型的期货合约相依关系研究

康 龙

（柏林国际应用技术大学 工商管理学院，德国 柏林10587）

一、引言

近年来，我国金融市场发展迅速。全国范围的四个期货交易所中，有许多新的期货合约上市交易。交易合约数和交易总量都达到了十分可观的规模。以上海期货交易所为例，从1999 年到2017 年，单边年成交量由0.03 亿手增长到13.64 亿手，增长454倍；单边年成交金额由0.24 万亿元增长到89.94 万亿元，增长374 倍①。上市期货品种由1999 年的3个增加到2018 年的15 个（含原油期货）。各大期货交易所还增添了基于某些期货品种的期权交易，为各类投资者提供了更多的交易工具。例如，目前上海期货所有铜期权交易和天然橡胶期权交易。

不断增长的合约品种和交易量也给交易所的风险控制带来了新的问题。随着交易合约品种的增多，更多的投资者开始同时交易多种期货及其他衍生品合约，这就给交易所在计算和收取客户保证金方面带来了新问题。一方面，投资者希望在交易每种合约的时候缴纳较低的保证金，提高交易杠杆的同时，提高资金的使用效率。另一方面，交易所希望在收取合理保证金的前提下，不过度收取客户的多余保证金，通过提高客户的资金使用效率来增加整个市场的交易量，并提高市场活跃度。由于大多数客户同时交易多种合约，且各个合约的相依关系不同，当合约之间可以对冲部分风险的时候，客户整体账户的保证金就不需要设定为单独交易每种合约所交保证金的总和，从而在收取合理保证金的同时释放多余的保证金给客户。怎样才能较为准确地估测和计算每个交易多种合约的客户所须缴纳的保证金呢？对于这个核心问题，时变T-Copula 模型为我们提供了一个较为可行且效果良好的量化解决方案。本文运用该模型对上海期货交易所交易的12 种主力期货合约价格变化的日内数据进行估测，结果显示模型可以较好地描述各种期货合约之间的相依关系。

二、文献综述

金融合约的相依关系一直是实证研究的一个重点，其研究结果主要运用于风险管理、投资管理以及各种套保或套利的交易策略优化。例如，梁仁方等[1]运用Copula-CoVaR 模型研究原油期货与PTA 期货的风险溢出效应。谢赤等[2]运用时变Copula 模型研究沪深300 股指期现货高频价格相依结构测度。在金融合约的相依关系方面，Copula 模型比多元正态分布能够更加灵活地描述某些特定的相依关系，比如明显的尾部相依性或者非对称的相依关系。因此，Copula 模型结合GARCH 模型被广泛运用于描述多种金融合约的相依关系。

Copula-GARCH 模型最早由Jondeau et al.[3]和Patton[4-5]开始使用。为了度量时变时间序列的条件相关性，Jondeau et al.[3]使用了Copula 函数并将其系数指定为前期变量的函数。Jondeau et al.[3]还用Hansen[6]文章中的GARCH 模型来拟合数据的边际分布。在他们的模型中偏度系数和峰度系数都是时变的。他们在文中发现对于大多数金融数据，时间序列之间的相依性在市场较大波动后，尤其是市场大幅下跌后会显著攀升。此外，Patton[4]还运用类似的模型对大盘股指数与小盘股指数的非对称的相依性进行了研究，并检验这种非对称的相依关系对投资组合是否有显著影响。Hu[7]运用混合Copula 模型研究了主要股票市场指数的相依性。她在模型中给正态Copula、Gumbel's Copula 和扭转Gumbel's Copula不同权重并加和来形成新的Copula 形式。Jondeau et al.[8]运用T-Copula 描述两个股票指数的相依性，Copula 系数遵从双状态马可夫过程。

通常描述多维联合分布的相依关系是比较困难的。Garcia et al.[9]构建了一个多维Copula 模型来描述四种资产的价格变化的相依关系。他在模型中运用了状态转换（regime-switching）的构造，在其中一个状态（regime）中他运用了多维正态Copula，在另一个状态中运用了混合Copula。在其混合Copula中，每一个Copula 侧重于描述每对特定资产价格组合的相依关系。Savu et al.[10]运用分级形式的Archimedean Copula，这种形式的Copula 在一定程度上可以灵活描述各个价格组合的相依关系。在模型中，每一对关系紧密的价格被一个特定类的Archimedean Copula 所描述，然后在上层运用其他Archimedean Copula 来连接先前部分。Archimedean Copula 的一个很好的特性是在这种分级的结构下，最后上层生成的函数形式依然满足Copula 函数的定义。

但过多的系数也给Copula 模型的估测带来了很大的困难。最大似然法在理论上可以用于估测Copula 模型。然而，在实际中当所拟合的时间序列增多的时候，在估测过程中最大似然法的数值优化问题将会很难得出满意的结果。Joe et al.[11]提出了一种两步估测法。第一步用最大似然法估测各个时间序列边际分布的系数，第二步再用最大似然法估测Copula 函数部分的系数。Joe[12]证明了在常规条件下，这种两步估测法产生的估测值是一致的，并且渐近服从正态分布。Patton[13]也得出了相似的结论。另外，在第一步估测中，我们还可以不估测边际分布的具体系数，而采用实证法来估测边际分布。这种方法可以避免错误假设边际分布的问题，被Cherubini et al.[14]称为典范最大似然法（Canonical Maximum Likelihood）。Hu[7]使用这种估测方法并将其命名为半参数法，并基于Genest et al.[15]，她证明了这种半参数法的估测值是一致的，并且渐近服从正态分布。另外，Copula 模型还可以用无参数法来估测。Deheuvels[16]介绍了实证Copula 的定义并且证明了实证Copula 一致性收敛于真实的Copula 形式。Xu[17]阐明了Copula 模型可以用贝叶斯的方法来估测。

三、模型

Copula 模型在金融建模方面已经得到广泛的应用。它的独到之处在于能够将多元随机变量的联合分布，分解为各自随机变量的边际分布和一个连接这些边际分布的Copula 函数。也就是说，为了构建正确的多元随机变量的联合分布，我们可以先对每一个随机变量单独建模，找到一个最好地描述其边际分布函数的模型，然后再寻找一个最合适的Copula 函数形式来连接这些边际分布。Copula 函数具有很多形式，T-Copula 函数虽然不是最完美的，但是对于同时描述大量的随机变量的相依关系，确实是一个很不错的选择。它比正态Copula 函数能更加灵活准确地拟合现实的金融数据。T-Copula 模型主要可用于风险管理和量化投资。本文主要运用Copula 函数结合GARCH 模型来对多种期货合约的价格变化的联合分布进行建模估测。

（一）Copula 函数

Copula 函数是一个多元分布函数，而被描述的多元随机变量的每一个边际分布是这个多元函数中的变量。Copula 函数将所有的边际分布连接起来形成多元随机变量的联合分布。Copula 理论主要基于Sklar[18]的结论，我们在下边叙述针对连续边际分布的Sklar's 定理。

令F1（x1），…，Fn（xn）分别为x1，…，xn的连续边际分布函数。令H 为（x1，…，xn）的联合分布。那么存在一个唯一的Copula 函数满足以下条件：

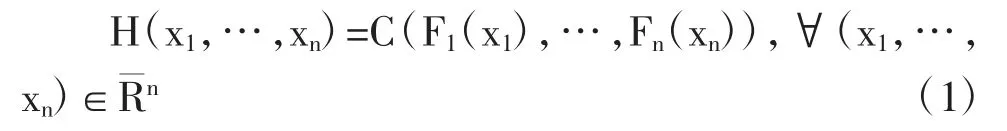
相反，如果我们令F1（x1），…，Fn（xn）为连续边际分布函数且C 为一个Copula 函数，那么，由等式所定义函数H 是一个联合分布且其各个边际分布分别为F1（x1），…，Fn（xn）。

根据以上理论，我们可以将一个多元随机变量的联合分布，分解为每个随机变量的边际分布和连接他们的Copula 函数。相反，这个理论也说明要建立一个多元随机变量的联合分布，可以先为每一个随机变量找到一个最合适的边际分布，然后再寻找一个最合适Copula 函数来连接所有的边际分布。另外，为了更好地拟合数据，我们通常假设随机变量分布的矩是时变的并且依赖于过去的变量数值。所以，在时间t 的随机变量的联合分布将变成基于过去变量数值的条件分布。这样以上所述的Copula 理论则需要进一步扩展为在条件分布情况下的理论。

（二）边际分布

作为组建Copula 模型的第一步，我们需要为每一个合约的价格变化的边际分布，找到最合适的模型。因为选用错误的模型来描述边际分布，将会导致错误的联合分布。令xi，t为资产i 在时间t 的回报率，那么它的条件均值和条件方差服从以下描述。

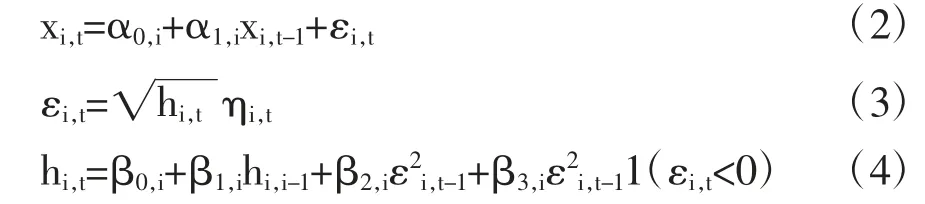
在等式（2）到（4）中，我们用AR（1）过程来描述条件均值，并用一个GJR（1，1）构造来描述条件方差[19]。以上等式中的系数有以下限制：β0，i＞0，是一个指示函数，当εi，t-1＜0 时，此函数值为1，否则为0。以上模型可以足够好地描述每个所包含资产回报率的边际分布。当然，也可以在等式（2）到（4）中包含更多的外因解释变量，从而更好地描述数据。另外，我们假设ηi，t在时间轴上服从i.i.d.并且服从学生t 分布，自由度系数为νi。当然我们还可以进一步描述条件高阶矩，例如，Hansen[6]、Jondeau et al.[8]假设GARCH 模型中的残差服从偏t 分布，并且发现偏t分布比正态分布能更好地描述金融数据。我们可以假设ηi，t～SkewedT（ηi，t｜νi，t，λi，t）。其中，ηi，t均值为0，方差为1，νi，t为自由度系数，λi，t为偏度系数。两个系数νi，t和λi，t随时间而变，且非线性依赖于前期的解释变量。

（三）相依结构

正态Copula 和学生T-Copula 同属于椭球分布族，他们经常被用来描述多元随机变量的联合分布。在实际应用中，通常学生T-Copula 比正态Copula 系数结构更加灵活，能够更好地描述多元随机变量之间的相依关系，尤其在拟合金融数据的应用中[20]。令Tν-1为标准学生t 分布Tv的逆分布，其自由度系数为ν＞2。TR，ν为n 维学生t 分布，其相关系数矩阵为R，自由度系数为ν。那么，n 维学生T-Copula可以定义如下：

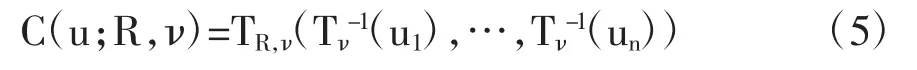
且其密度函数可定义为：

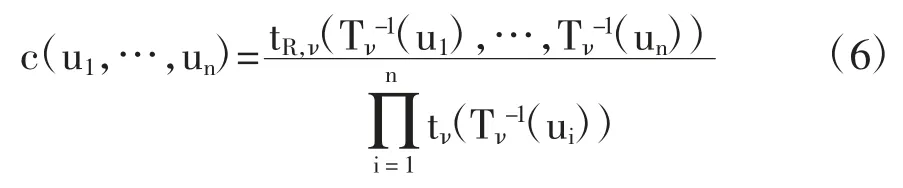
其中，tν和tR，ν分别为Tν和TR，ν的概率密度函数。

我们借助DCC-GARCH 模型的思路[21]，可以构建一个时变T-Copula，其时变相关系数矩阵由以下等式来描述：

另外，等式（7）确保条件相关系数矩阵Rt是正定的[22]。

（四）模型估测

令Θ=｛θ，γ1，…，γn｝为联合分布的系数集，其中θ 为Copula 部分的系数，γi是第i 个资产价格的边际分布的系数集。那么，所有n 个价格在时间t 的条件累计分布函数为：

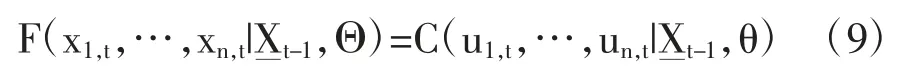
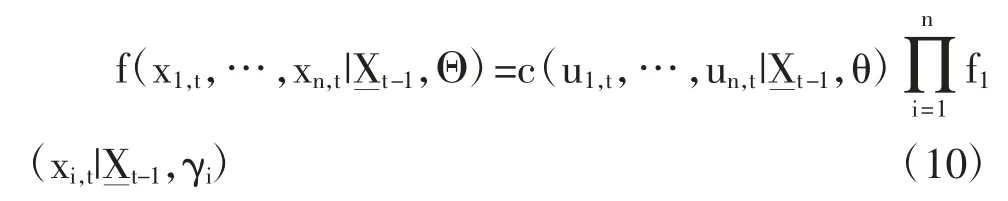
基于等式（10），对数似然函数值可以写成：

等式（12）显示出Copula 和边际分布是相加性可分的。所以我们可以运用两步法估测整个模型。第一步，用最大似然法估测每个变量的边际分布的系数，然后再基于第一步的估测得出的每个价格变化的累计分布函数，用最大似然法估测Copula 的系数。Joe et al.[12]和Patton[13]都论证了这种两步法的估测值是一致的，且渐进服从正态分布。

本文先用最大似然法估测每个价格序列的GJR（1，1）模型，然后估测时变T-Copula 的系数。对于T-Copula 的最大似然法估测通常得不出分析解，并且数值法最大化问题也十分困难。我们遵循Chen et al.[22]的办法，基于，可以计算出的样本协方差矩阵，这个样本协方差矩阵是自由度ν 的函数。先设定，可以运用等式将Qt和Rt在所有时间t 的数值表述为α，β 和ν的函数，然后通过最大化T-Copula 密度的对数似然值来估测α，β 和ν。

四、数据来源

本文拟合的数据为上海期货交易所交易的12种期货主力合约20 分钟的价格变化（对数回报率）。我们运用AR（1）来描述条件均值，然后用GJR（1，1）来描述每一个价格变化的条件波动率[19]。在运用TCopula 函数形式的时候，我们用一个时变相关系数矩阵来描述各个变量之间的动态相依关系[21]。由于所需估测的系数比较多，直接用最大似然法估测很难得到满意的结果。我们采用两步法来估测，第一步估测每个合约价格变化的边际分布模型，第二步估测Copula 函数中的系数。

目前在上海期货交易所交易的期货合约共有14 个品种，分别为铜、铅、铝、锌、锡、镍、天然橡胶、沥青、螺纹钢、热卷、黄金、白银、燃料油和线材。由于燃料油和线材交易十分不活跃或者交易时长不满1 年等原因，在分析中不考虑这两个品种②。具体数据的时间跨度为2018 年1 月2 日至2018 年12 月28 日。由于我们所描述的数据频率为20 分钟，所以1 年长度的数据可以提供足够的样本数量用于估测。而且1 年长度的数据也可充分包括数据中的大部分的季节性因素。本文的原始数据来源于国内某大型期货公司量化交易柜台实时获取的高频数据，数据频率为0.5 秒。我们对每一个交易品种在每一天按照最大持仓量的原则选取主力合约，然后将每个品种的主力合约连接起来形成整体数据。所有12个品种的主力合约的价格按照接收行情的时间戳对齐。通常对于每一个相对交易比较活跃的合约价格，每0.5 秒交易所都会发送新的行情价格。而对于某些交易不活跃的合约或者某些活跃合约在极少数不活跃的时间段，在某些0.5 秒的时间段中交易所不会推送任何行情。我们根据数据中的买价和卖价算出中间价，再选出20 分钟频率的价格来计算价格变化。如果恰巧在所选的时间点上没有数据，我们将用前后最近的价格均值来代替。另外，由于每种合约夜盘交易时段有所不同且模型估测的核心在于所有合约的联合分布，夜盘时段只采用所有合约都进行交易时段的数据。最后，所拟合的价格变化具体为每20 分钟价格的自然对数的一阶差分，当交易停止时或者主力合约更换的时候，就会产生异常值。为了避免给整个模型估测带来问题，我们将交易中断或主力合约更换期间的价格变化值都设为0。

五、实证结果

（一）数据的初步分析

同一品种合约在不同时期有不同的波动率，而且具有明显的波动率聚集现象。即使在排除了交易间断过程（包括更换主力合约等情况）的价格大幅度波动的情况下，某些品种的价格变化仍有超常规的跳动。表1 显示了12 个期货品种对数回报率的描述性统计量，分别为均值、标准差、偏度和峰度。所有品种回报率趋近于0，标准差在0.000 8 到0.004 1 之间。其中，天然橡胶波动率最高，黄金最低。12 个品种的偏度在-0.58 到0.52 之间。12 个品种的峰度都明显大于3，充分说明了所有回报率分布的厚尾性。根据以上的初步分析，采用GARCH 模型来描述回报率的波动率聚集和分布的厚尾性。

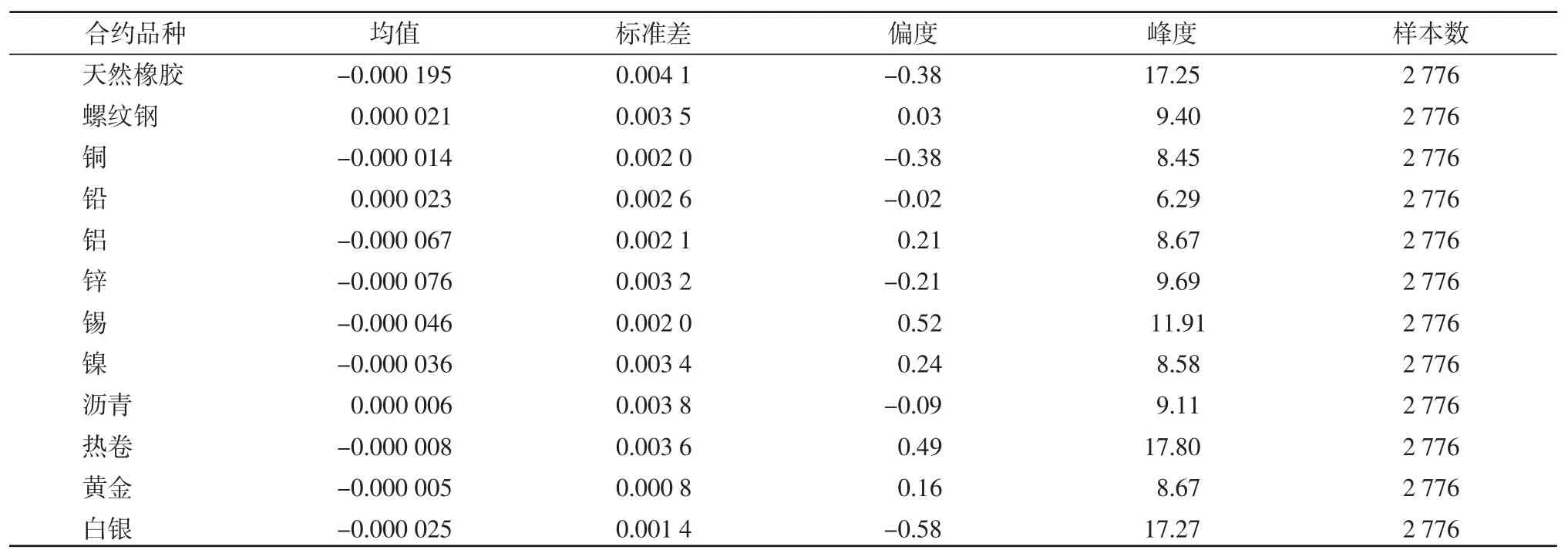
表1 12 种期货合约20 分钟对数回报率的统计描述

（二）边际分布的估测

在估测每一个合约的边际分布时，本文采用了AR（1）过程和GJR（1，1）模型来描述价格变化的条件均值和条件方差。在实际应用中，可以加入更多外生变量来提高模型的拟合和预测效果③。表2 显示了单个合约边际分布的估测结果。对于条件均值等式，除了铜、铅、沥青、热卷和黄金，其他品种的第一个滞后项的系数都是统计上显著的。说明AR（1）可以较好地描述合约的条件均值。在条件方差方面，对于绝大多数合约的描述，GARCH 和ARCH 项的系数是统计上显著的。然而，对于杠杆项，有很多合约的系数并不是统计上显著的，或许GARCH（1，1）的模型会比GJR（1，1）的模型能够更好地描述一部分期货合约的价格变化④。另外，大部分合约的自由度系数都是统计上显著的，并且估测数值比较小，充分说明合约具有显著的厚尾性。我们可以根据模型估测结果，绘制12 个合约估测的条件波动率。对于20 分钟间隔的价格变化，可以明显观测到波动率的积聚性以及波动率突发升高的现象。这也充分说明了，交易所加强日内价格变化的风险控制的重要性和必要性。

（三）时变Copula 函数的估测

表3 列示了Copula 函数的估测结果。基于标准误差，Copula 函数的三个系数都是统计上显著的。系数α 的估测值非常接近于0，系数β 的估测值非常接近于1，而自由度系数ν 的估测值大约为23。T-Copula 函数的自由度系数的估测值体现了TCopula 同时描述多组合约价格变化的相依关系时的相对表现。由于T-Copula 的自由度系数很大程度决定了所描述的各个组合期货合约的尾部相依度，在拟合大量合约的情况下，有些合约之间尾部相依度较高，有些则较低，T-Copula 自由度系的估测值也是同时描述较高和较低尾部相依性的一种折中。所以，T-Copula 可以在一定程度上更好地描述多种价格变化的相依关系[20]。

表2 12 种期货合约边际分布的估测结果

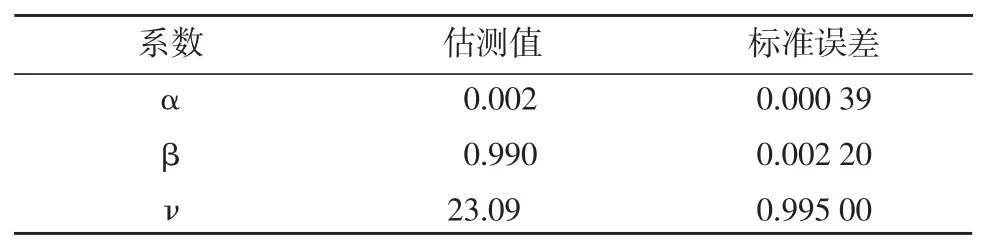
表3 时变T-Copula 函数中系数的估测值及其标准误差

（四）时变相依关系

时变T-Copula 模型的相关系数矩阵和自由度系数可以比较好地同时描述多种合约价格变化的相依关系，尤其是在一定程度上可以较好地描述每两个合约之间的尾部相依关系。图1 绘出了螺纹钢和热卷、黄金和白银、铜和镍、铜和锡、锡和白银、橡胶和沥青，这6 组合约的动态相关系数。前3 组合约品种由于属于相同或者相近的合约类别，他们的相关系数均超过0.5，而后3 组合约属于不同的类别，他们的相关系数均低于0.5。同时，可以发现在时变的动态模型构造下，各组合约之间的相关系数时变性还是很明显的⑤。图2 绘出了上述6 组合约的尾部相依系数（tail dependence coefficient）。螺纹钢和热卷这对合约的尾部相依系数在0.3 左右波动，可见这两种产品的尾部相依关系是多么的密切。而黄金和白银、铜和镍，这2 组合约的尾部相依系数在0.03 左右波动。后3 组非同类或接近同类的合约组合尾部相依系数都几乎接近于0。由于模型的时变属性，尾部相依系数也是一直在波动的。以上结果充分说明了，时变T-Copula 模型可以在一定程度上同时描述多种合约的相依关系，尤其是尾部的相依关系。

六、结论与展望

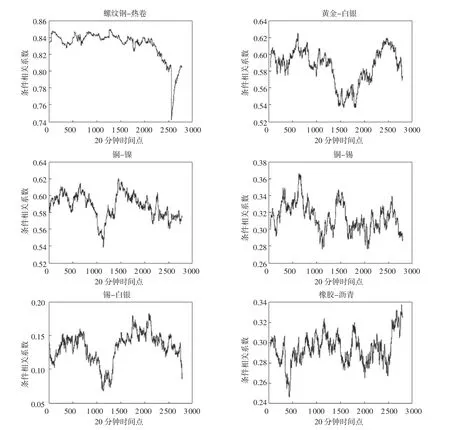
图1 6 对期货合约的估测条件相关系数

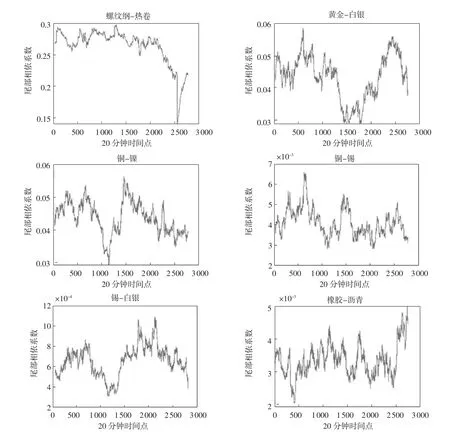
图2 6 对期货合约的估测尾部相依系数

基于时变T-Copula 模型，本文构建和估测了期货合约相依关系。第一，用AR（1）过程和GJR（1，1）模型来描述每个合约价格变化的条件均值和条件方差。第二，用时变T-Copula 模型来连接每个合约的边际分布，从而描述它们的相依关系。在时变TCopula 模型中，时变的相依关系主要由时变的相关系数矩阵和自由度系数来共同描述。本文运用一个动态条件相关系数（DCC）的构造，来实现随时间变化的相依系数矩阵。估测结果显示，对于上海期货交易所12 个期货品种的主力合约在2018 年所有交易日的20 分钟价格变化数据，此模型可以较好地描述边际分布和联合分布。但GJR（1，1）模型中的杠杆效应不是十分显著，这也意味着用GARHCH（1，1）模型代替GJR（1，1）模型或许更加合适。在相依关系的描述方面，本文绘制了6 组合约估测的条件相依系数和尾部相依系数。时变T-Copula 模型可以很好地同时描述多个合约价格变化的相依关系，尤其是显著的尾部相依性。

在理论上讲，很难找到一个Copula 函数形式能够足够灵活地同时描述很多变量的相依关系。本文中所构建的时变T-Copula 模型也具有一定的局限性。此模型的系数结构对于每一对所包含的随机变量，其产生的尾部相依系数中上尾相依系数和下尾相依系数总是相等的。在现实数据中，两个变量的上尾相依系数和下尾相依系数并不总是相等的。另外，当所包含的变量数量不断增加的时候，此模型描述尾部相依关系的能力将会降低。当然，通过本文的阐述和对实际数据估测，时变T-Copula 模型可以足够好地描述多种合约的条件相关系数和在一定程度上体现数据中的显著的尾部相依关系。

注释：

①数据来源于上海期货交易所网站。

②每个交易品种的合约信息可以在上海期货交易所网站获得，http：//www.shfe.com.cn/。

③在目前中国期货市场的高频数据中，我们可以引入不少外生变量，比如成交量、持仓量、买量和卖量等。

④在实际估测中，对于杠杆项不显著的合约，可以用GARCH（1，1）模型替换GJR（1，1）模型。在本文中，仍然用GRJ（1，1）并且相信对模型的估测不会有很大影响。

⑤T-Copula 模型的相关系数矩阵在数值上很接近，但一般情况下不等于各个合约价格变化的相关系数矩阵。