基于粗糙集理论的模糊聚类算法研究

张红霞 吴桐桐 冷雪亮

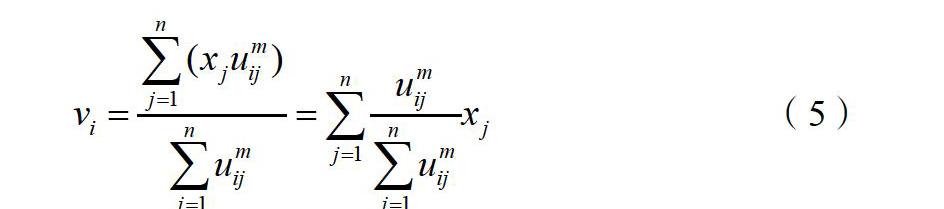
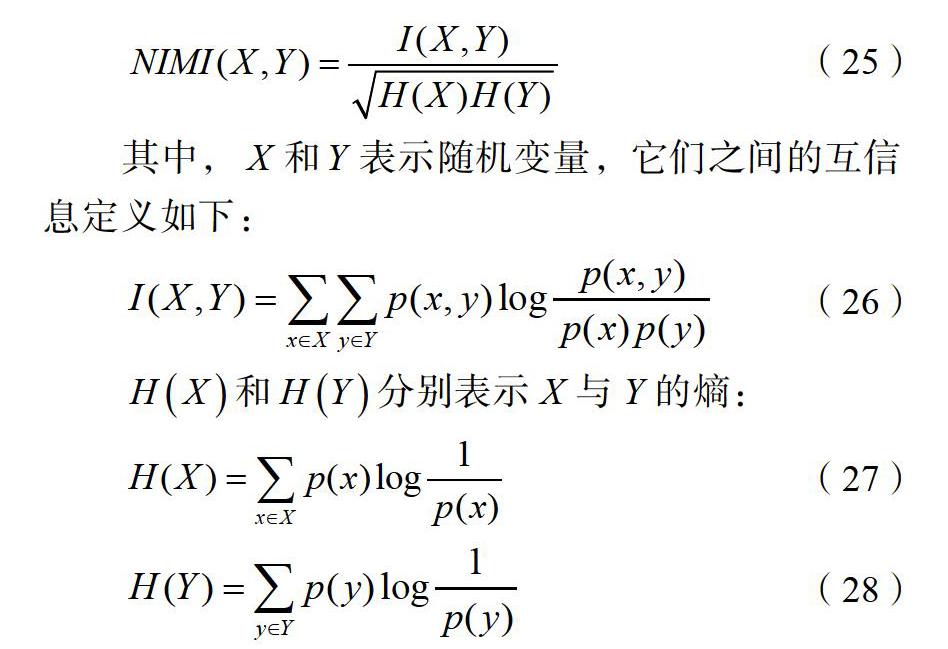
摘  要： 粗糙集理论是一种新型的处理含糊不确定知识的数学工具，善于分析隐藏在数据中的事实而不需要关于数据的任何附加知识，粗集理论不仅为信息科学和认知科学提供了新的科学逻辑和研究方法，而且为智能信息处理提供了有效的处理技术。聚类是作为数据挖掘系统中的一个模块，既可以作为一个单独的工具以发现数据库中数据分布的深层信息，也可以作为其他数据挖掘分析算法的一个预处理步骤。模糊聚类算法忽略了聚类边界不确定的问题和复杂数据问题从而导致聚类效果不理想。本文提出了将粗糙集和模糊聚类算法相结合，利用粗糙集中上近似集和下近似集的概念得到相似性度量来改进模糊聚类算法。实验证明，改进的算法能够得到更好的聚类效果。

关键词： 粗糙集;模糊聚类;上近似;下近似

中图分类号： TP301.6    文献标识码： A    DOI：10.3969/j.issn.1003-6970.2019.09.036

本文著录格式：张红霞，吴桐桐，冷雪亮. 基于粗糙集理论的模糊聚类算法研究[J]. 软件，2019，40（9）：156-163

Research on Fuzzy Clustering Algorithm Based on Rough Set Theory

ZHANG Hong-xia， WU Tong-tong， LENG Xue-liang

（College of Computer and Information， Shandong University of Science and Technology， Qingdao 266000， China）

【Abstract】： Rough set theory is a new mathematical tool for dealing with vague and uncertain knowledge. It is good at analyzing the facts hidden in the data without any additional knowledge about the data. Rough set theory not only provides new scientific logic and research methods for information science and cognitive science， but also provides effective processing technology for intelligent information processing. Clustering is a module in the data mining system. It can be used as a separate tool to discover the deep information of data distribution in the database， or as a pre-processing step of other data mining analysis algorithms. The fuzzy clustering algorithm ignores the problem of cluster boundary uncertainty and complex data problems， which leads to the unsatisfactory clustering effect. This paper proposes to combine the rough set and the fuzzy clustering algorithm， and use the concept of the approximate set and the lower approximation set on the rough set to obtain the similarity measure to improve the fuzzy clustering algorithm. Experiments show that the improved algorithm can get better clustering effect.

【Key words】： Rough set; Fuzzy clustering; Upper approximation; Lower approximation

0  引言

聚類分析按照不同的标准有不同的划分，按照数据样本隶属度的取值范围划分，可以将聚类分析方法分为两类，一类叫硬聚类分析，另一类叫软聚类分析，也叫模糊聚类分析。硬聚类是一种严格地划分，旨在将每一个数据样本划分到一个确定的簇中，划分机制非常明确，其隶属度只有两个值0和1，也就是说，一个样本只能完全属于某一个类或者完全不属于某一个类。例如，将小于或者等于40岁的人划分为年轻，大于40岁的人划分为不年轻，那么不管是39岁还是9岁，都属于年轻类，这就是典型的“硬隶属度”概念，这种聚类方法过于严格，对于一些位于边界处的数据对象不是很友好，容易产生误差。软聚类对于数据对象的划分比较宽容，它是依据数据样本隶属度的大小，将其划分到不同的簇。比如30岁，可能属于年轻这类的隶属度值为0.7，而属于不年轻这个类的值为0.3，这样划分就比较合理。另外，当隶属度的值只取0或1时，模糊聚类就变成了硬聚类。通过介绍，可以看到模糊聚类获得的聚类结果具有不确定性，它将聚类结果进行了模糊化，这样就能够对现实世界中的数据划分问题进行更加客观的描述，因此模糊聚类分析已成为聚类研究的主流方向之一。

本文算法结合了粗糙集^[1-3]等理论，提出了基于粗糙集理论的模糊聚类算法。该算法是通过粗糙集理论最终得到一个隶属值，然后，用表示的抑制率乘以非获胜者所属类簇的隶属度值，以修改模糊隶属度，从而在一定程度上增加获胜者的隶属度值。通过实验表明该算法能够解决原始算法中的缺点，并且还能提高聚类的准确率和减少花费的时间。

1  相关工作

1.1模糊C均值聚类算法原理

模糊C均值聚类算法是目前应用最广泛的软聚类^[4-5]算法之一，该算法利用目标函数来解决数据样本的聚类问题，把聚类的过程转化成带约束的优化问题，因此可以借助数学领域中经典的非线性规划理论对其进行求解。

假设数据样本集合，是样本个数，已知该数据集共有类，聚类任务就是希望把中的所有数据对象划分到个类中，每个类都有一个唯一的聚类中心，聚类中心集合为。那么，模1糊C均值聚类算法可以表示为下面的数学规划问题：

（1）

且满足：

（2）

其中，是数据样本属于某一类的隶属度。隶属度的值越大则说明数据样本属于类的可能性越大，反之则可能性越小。是模糊划分矩阵，从模糊划分矩阵^[6]-[8]中可以找到每個数据样本相对于每个类簇的隶属度值;样本与第个类类中心的相似性大小，用欧氏距离计算，记为;是模糊权重指数，也称为模糊因子，改变它的取值能对模糊类之间的分享程度进行调节。模糊聚类算法的聚类过程就是目标函数公式（1）的求解过程。目标函数中有两个未知的量，分别是和，采用拉格朗日乘数法和求导公式对式（1）求解，可以得到下面的结果：

（3）

（4）

观察上式可以发现，与是相互关联的，彼此包含对方。在模糊聚类算法开始的时候，通常人为赋值给或者其中的一个，只要数值满足约束条件即可，然后就可以根据公式开始迭代更新。例如，假设给赋值，有了就可以计算，得到后又可以根据此去计算新的，如此反反复复。在这个过程中，目标函数J一直在变化，最后逐渐趋向稳定值。那么，当J不再变化的时候就认为算法收敛到一个比较好的结果。可以看到和在目标函数J下构成了一个迭代更新的过程。

假设計算数据样本中的样本1到各个类中心的隶属度，此时j=1，，在式（3）中，分母求和公式里的分子表示的是数据样本1相对于某一类的类中心距离，而求和公式的分母是这个数据样本1相对于所有类的类中心的距离的和，因此它们的商表示的就是数据样本1到某个类中心的距离，在样本1到所有类中心的距离和的比重。当越小，说明数据样本属于类的可能性越大，公式1的值就越大，对应的就越大，数据样本就越属于这个类。

通過上述分析可以知道，当类确定后，式4的分母求和是一个常数，根据式（4）可以得到聚类中心的更新公式：

（5）

对于式（5）通俗的解释就是，类确定后，将所有数据样本点到该类的隶属度求和，然后对每个点，用其隶属度除以这个和再乘以，就是这个点对于这个类的贡献值。

1.2模糊C均值聚类算法步骤

模糊C均值聚类算法首先需要事先确定聚类^[9-11]中心，再计算每个数据样本属于每个聚类中心的隶属程度，得到一个隶属度矩阵;然后根据隶属度的大小对所有数据样本进行划分，得到每个数据样本的聚类情况，根据最新的划分，再重新计算每个类的聚类中心。模糊C均值聚类的过程就是通过迭代聚类中心和隶属度矩阵，直到算法收敛为止。

算法1-1  模糊C均值聚类算法

输入：数据集

输出：隶属度矩阵和聚类中心

Step1：对参数进行初始化。给定聚类数目;模糊因子m=2;隶属度矩阵，并使其满足式（2）;=0，用来记录迭代次数;

Step2：根据式（6）更新聚类中心;

（6）

Step3：根据式（7）更新隶属度矩阵;

定义3.2  给定一个论域和论域上的一个等价关系，模糊聚类过程中 产生的聚类结果构成一个划分，是与聚类中心划分为一类的数据样本的集合，则集合的上近似集为：

（10）

下近似集为：

（11）

边界域为：

（12）

集合的下近似集为：

（13）

上近似集为：

（14）

边界域为：

（15）

假设数据样本集合，數据样本个数为n，模糊聚类算法要将中的所有数据对象划分到c个类中，每个类都有一个唯一的聚类中心，c个聚类中心的集合为。那么RS-SFC算法可以表示为下面的数学规划问题：

（16）

其中：

（17）

（18）

表示样本属于某一类i的隶属度，参数和分别表示第i个簇的近似精度和粗糙度，满足。

RS-SFC算法基于下近似集和边界域的加权平均，定义了新的模糊质心更新公式，使其同时考虑模糊隶属度和上近似集、下近似集的影响。通过对求解式（16），得到新的模糊聚类中心计算公式为：

（19）

其中：

（20）

（21）

为提高聚类的速度，本文借鉴文献^[75]中提出到的抑制因子来提高RS-SFC算法的速度，抑制因子通过引入竞争机制，在保持良好的聚类精度的同时以提高收敛速度。RS-SFC算法在每次迭代更新隶属度矩阵后，对对象进行抑制，步骤如下：

对于每个数据对象，在获得其新的模糊隶属度矩阵后，找到模糊隸属度矩阵中最大的模糊隶属度，并宣布第k个类为获胜者，获得了数据对象。这样，每个数据对象都有一个属于自己的类簇，且不依赖任何其他数据点。然后，用表示的抑制率乘以非获胜者所属类簇的隶属度值，以修改模糊隶属度，从而在一定程度上增加获胜者的隶属度值。因此，RS-SFC算法有以下隶属度计算公式：

（22）

这些修改后的隶属度值被用来计算新的聚类  中心。

2.2算法步骤

RS-SFC算法的过程是迭代更新公式（19）和公式（3）的过程，直到式（16）趋于稳定，迭代停止。根据上述定义和分析，基于粗糙集的抑制模糊聚类算法的步骤如下：首先，随机选择C个数据对象作为C个簇的聚类中心，然后根据式（3）和（22）计算所有数据样本的模糊隸属度，根据每个样本相对聚类中心的大小对数据样本进行划分。根据得到的新的划分，用式（19）更新聚类中心，然后再根据新的聚类中心求解新的隶属度矩阵，如此循环，当聚类结果趋于稳定后，该算法终止。

算法2-2  基于粗糙集的抑制模糊聚类算法

输入：数据集

输出：隶属度矩阵和聚类中心

Step 1：初始化相关参数。给定聚类中心的个数c，设置模糊因子m=2.0，停止阈值，迭代计数，初始化隶属度矩阵，使其满足约束条件;设置抑制因子（0<<1）;

Step 2：根据隶属度矩阵，使用式（4.19）计算聚类中心;

Step 3：根据式（4.3）、（4.22）更新隶属度矩阵，迭代计数;

Step 4：如果，则算法终止;否则转至Step 2。

3  实验结果与分析

本节将通过实验对RS-SFC算法进行研究。首先对实验中所用数据集进行描述，并对数据集进行预处理;然后将RS-SFC算法同其他两个常用的聚类算法进行比较，以分析该算法的有效性。最后在对实验结果进行分析的基础上，总结RS-SFC算法的优缺点，为以后的研究指明方向。

本次实验一共分为两部分，一是测试本文提出RS-SFC算法的聚类效果。将该算法与模糊C均值聚类算法、K-means聚类算法同时应用在8个数据集上，并计算每个数据集的准确率、F1值和互信息，以对聚类效果进行对比;二是测试RS-SFC算法的收敛速度。分别记录RS-SFC算法和模糊C均值聚类算法在对数据集进行聚类时的迭代次数。每个算法运行30次，最后取平均值。模糊C均值聚类算法在上文中已有介绍，K-means聚类算法是在现实生活中应用十分广泛的聚类算法，它是一种基于距离的聚类方法，具体描述见参考文献。

3.1数据集描述

由于本实验需要计算聚类准确率，以对算法的聚类效果进行分析，因此实验中采用带有属性标签的数据集。实验中所用到的数据集的信息如表1所示，其中包含经典的人工数据集和UCI上的真实数据集。这些数据集在属性数量、类簇数量上有一定的区分度。

在进行聚类之前，先对数据进行预处理。使用本文第三章中提出的MIMR属性约简算法，对表1中的数据集进行属性约简，以剔除数据集中没有用的列，减少数据集的规模。经过属性约简后，得到表2所示的实验数据集。

3.2评价指标

本文通过计算聚类结果的准确率（Accuracy），F-measure和互信息（NMI），来评价聚类结果的質量，通过算法迭代次数评价收敛速度。

聚类结果的准确率类定义如下：

（23）

其中，为数据集类簇的数量，表示正确分类到类中的样本数量，为全体数据样本。

F-measure又称F-score：

（24）

其中，，表示属于类簇但被错误分类到其它簇的样本数量。当参数取1时，就是常见的F1值。

标准化互信息是描述变量之间相互依赖性大小的度量。

（25）

其中，和表示随机变量，它们之间的互信息定义如下：

（26）

和分别表示X与Y的熵：

（27）

（28）

3.3实验结果及分析

3.3.1  聚类效果比较

为了验证本文提出的RS-SFC算法的有效性，将RS-SFC算法与模糊C均值算法和K-means聚类算法进行对比。为了评价算法的聚类效果，实验对每个数据集在三个算法上取得的聚类结果的准确率、F1值和互信息进行了比较。每个算法在每个数据集上一共运行30次，最后取平均值。

（1）聚类准确率比较

表3是三种算法在数据集上取得的聚类结果准确率，每个表的最后一行是这8个数据集获得的平均值。表中加黑的单元格数据表示这一行中的最  优值。

从准确率的平均值来看，本文的RS-SFC算法在这8个数据集上取得的准确率最高，比K-means算法和模糊C均值算法都有明显的提高。为了更直观的比较三个算法的优劣，将表3用折线图进行展示，如图2所示。

从单个数据集来看，K-MEANS聚类算法对于Dp1数据集的聚类结果最差，模糊C均值和RS-SFC算法在Dp1数据集上都取得了很高的聚类准确率;

对于wine数据集来说，K-means算法取得了最高的准确率，本文的RS-SFC算法虽然没有取得最大值，但是比K-means算法的准确率仅低3.4%，并且仍然高于模糊C均值算法。在hepatitis数据集上，三个算法的准确率都不高，没有超过80%。通过分析发现，hepatitis数据集是一个不平衡性数据集，准确率评价指标在数据划分相对平衡的数据集上，能够更好的说明聚类效果。在其他几个数据集上，RS-SFC算法都能得到较高的准确率，尤其在类簇数量比较多的数据集上取得了不错的表现，如glass数据集和Heart-disease数据集。综上所述，RS-SFC算法的聚类准确率远于其他两个对比算法相比，具有明显的优势。

（2）F1值比较

表4和图3展示的三个算法聚类结果的F1值。在表4中，最后一行是对每一列数据求均值得到的平均数。表中加黑的单元格数据表示这三个算法在同一个数据集上取得的最优值。F1值评价指标在评价聚类效果时更加全面，它不仅考虑了聚类结果的准确率，还考虑了召回率，因而能够更好的描述不平衡数据的聚类效果。

由表4和图3可发现，RS-SFC算法在数据集glass和heart-disease上得到的F1值要明显的大于另外两个算法，这个数据集的聚类数目分别是7和5，这说明RS-SFC算法在类簇数较多的数据集上也可以取得理想的效果。对于wine数据集来说，尽管K-means算法得到最高的F1值，但是在两个软聚类算法中，RS-SFC算法的F1值仍然高于模糊C均值算法。此外，在haberman數据集上，模糊C均值算法的F1值略高于其他两个算法，但是相差不大。

整体上来看，RS-SFC算法在8个数据集上得到的平均F1值高于另外两个算法，并且在四分之三的数据集中取得了最大值，这证明了RS-SFC算法的有效性和稳定性。

（3）标准互信息比较

标准互信息（NMI）可以衡量两个变量的之间的相关性，是一种常见的评价聚类效果的指标。在本章的实验里，用标准互信息来衡量数据样本的实际类别与聚类结果是否一致。

标准互信息的值域是（0，1），对于聚类算法来说，聚类效果越好，其值越接近于1，否则越接近0。图4是根据表5所作的三个算法在8个数据集上得到的互信息折线图。

从图4可以发现，RS-SFC算法求得的标准互信息的平均值要高于另外两个算法。从单个数据集来看，在wine数据集上，与准确率和FI一样，K-means算法的效果更好，但是在两个软聚类算法中，RS-SFC算法的标准互信息值较模糊C均值算法仍然有小幅度的提升。此外，在维度比较高的两个数据集breast和Heart-disease上，本章的RS-SFC算法较另外两个算法仍有较大幅度的提升。在其他数据集上，RS-SFC算法相对于另外两个算法也有小幅度的提升。

综合三个评价指标可以发现，本章提出的RS-SFC算法和模糊C均值算法在wine数据集上的表现较差，略逊色于K-means算法。这是由于K-means聚类算法属于硬聚类算法，当一个数据集中，属于同一个簇的数据样本相似度很高，而属于不同簇的数据样本相似度明显小的时候，这类算法具有明显的优势。但对于噪声样本比较多、簇与簇之间边界不清晰的数据集来说，RS-SFC算法则更加适用。另外，通过实验可知， RS-SFC算法在实验中的大多数数据集上聚类效果都优于对比算法，证明了RS-SFC算法的有效性。

3.3.2  迭代次数比较

在RS-SFC算法中，设置了一个抑制因子来加快算法的迭代速度。为了验证该算法在收敛速度上是否有所提高，实验中将RS-SFC算法和模糊C均值算法的最终迭代次数进行比较。实验中为抑制因子设置了不同值，记录了在不同的抑制因子下，RS-SFC算法和模糊C均值算法的迭代次数。

实验结果如表6所示。

通过上表很明显的可以看出，RS-SFC算法的迭代次数明显少于模糊C均值聚类算法，且随着抑制因子的增大，迭代次数也逐渐增多，验证了RS-SFC算法在收敛速度上优于模糊C均值算法。

4  结束语

本章首先介绍了模糊聚类的有关概念，对模糊C均值聚类算法的原理进行了解释，描述了模糊C均值算法的算法步骤;然后将粗糙集理论引入到模糊C均值算法中，根据粗糙集理论中上、下近似集的思想，将模糊C均值算法中的聚类中心更新公式进行了改进，降低了簇边缘噪声数据对聚类效果影响，同时设置了一个抑制因子以提高算法的收敛速度，提出了一种基于粗糙集的抑制模糊聚类算法;最后通过实验，在多个数据集上对RS-SFC算法进行了验证。

参考文献

[1] 王国胤， 姚一豫， 于洪. 粗糙集理论与应用研究综述[J]. 计算机学报， 2009， 32（07）： 1229-1246.

[2] 苗夺谦， 张清华， 钱宇华， 梁吉业， 王国胤， 吴伟志， 高阳， 商琳， 顾沈明， 张红云. 从人类智能到机器实现模型——粒计算理论与方法[J]. 智能系统学报， 2016， 11（06）： 743-757.

• 王国胤， 苗夺谦， 吴伟志， 梁吉业. 不确定信息的粗糙集表示和处理[J]. 重庆邮电大学学报（自然科学版）， 2010， 22（05）： 541-544+550.
• 周涛， 陆惠玲. 数据挖掘中聚类算法研究进展[J]. 计算机工程与应用， 2012， 48（12）： 100-111.
• 王骏， 王士同， 邓赵红. 聚类分析研究中的若干问题[J]. 控制与决策， 2012， 27（03）： 321-328.
• 程温鸣， 彭令， 牛瑞卿. 基于粗糙集理论的滑坡易发性评价——以三峡库区秭归县境内为例[J]. 中南大学学报（自然科学版）， 2013， 44（03）： 1083-1090.
• 耿秀丽， 张在房， 褚学宁. 基于变精度粗糙集的产品配置规则提取及增量式更新[J]. 上海交通大学学报， 2010， 44（07）： 878-882.
• 陈果， 宋兰琪， 陈立波. 基于神经网络规则提取的航空发动机磨损故障诊断知识获取[J]. 航空动力学报， 2008， 23（12）： 2170-2176.
• 雷小锋， 谢昆青， 林帆等. 一种基于K-means局部最优性的高效聚类算法. 软件学报， 2008， 19（7）： 1683-1692.
• 谢娟英， 高紅超， 谢维信. K近邻优化的密度峰值快速搜索聚类算法. 中国科学： 信息科学，2016， 46（2）： 258-280.
• 吕学伟， 黄松， 王晔. 基于OPTICS算法的变异体约简技术[J]. 解放军理工大学学报： 自然科学版， 2016， 17（2）： 101-104.
• 徐菲菲， 苗夺谦， 魏莱， 等. 基于互信息的模糊粗糙集属性约简[J]. 电子与信息学报， 2008， 30（6）： 1372-1375.
• 张晓红. 基于信息熵的粗糙集理论的研究和应用[D]. 安徽大学， 2011.
• 李玉超， 徐金华. 基于Vague粗糙集信息熵的属性约简算法[J]. 运筹与管理， 2017， 26（05）： 1-5.
• 潘瑞林， 李园沁， 张洪亮， 伊长生， 樊杨龙， 杨庭圣. 基于α信息熵的模糊粗糙属性约简方法[J]. 控制与决策， 2017， 32（02）： 340-348.