一个解变分不等式问题的非单调Broyden-like算法

(武夷学院数学与计算机学院，福建 武夷山 354300)

1 预备知识

考虑变分不等式问题(简记VI(X,F))[1-5]：求向量x*∈X，使得对于任意的x∈X有：

(x-x*)TF(x*)≥0，

(1)

成立。 其中，向量函数F(x):Rn→Rn为连续可微函数。

2010年，Zhang、Liu等人提出了可行域[1]：X={x|Ax>b,x∈Rn,A∈Rm×n,b∈Rm}的VI(X,F)，记D=AT，文中的VI(X,F)皆是该类VI(X,F)，其KKT系统为：F(x)-Dy=0,yT(Ax-b)=0,y≥0,Ax-b≥0。记s=Ax-b，则有

F(x)-Dy=0,s=Ax-b,y≥0,s≥0,yTs=0。

(2)

采用Fischer-Burmeister(FB)函数[6-7]：

将式(2)等价转化为方程组问题，即

(3)

其中，

(4)

显然函数φFB(a,b)=0⟺a≥0,b≥0,ab=0，但是FB函数在点(0,0)处不可微，通过引入光滑参数μ>0，得到一个光滑FB函数：

(5)

那么，φ(0,a,b)=φFB(a,b)。

令z=(μ,x,y,s)∈R++×Rn×Rm×Rm，

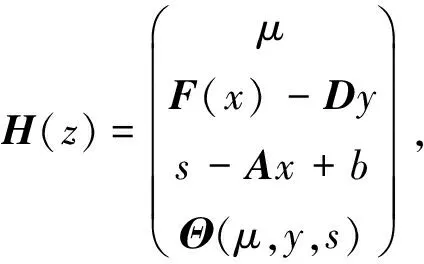
(6)

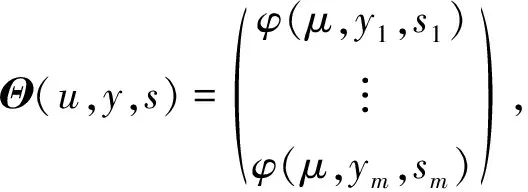
(7)

那么式(2)等价于以下方程组问题：

H(z)=0。

(8)

通过计算，得

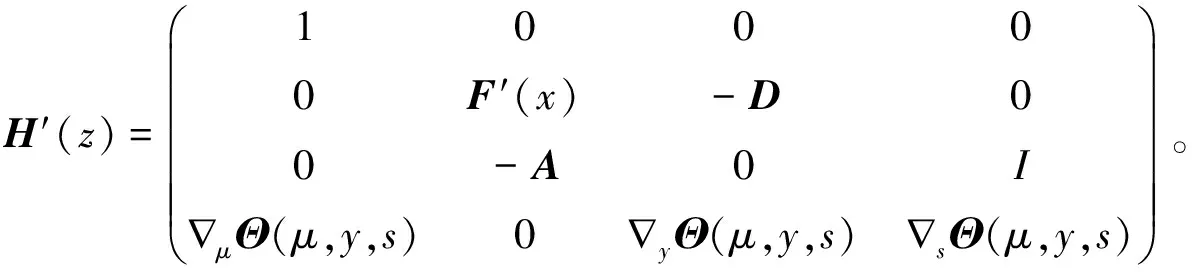
(9)

其中，

μΘ(μ,y,s)=vec{[φ(μ,yi,si)]′μ:i∈N}，

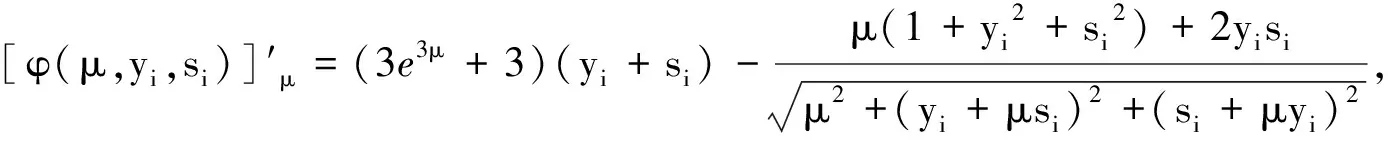
(10)

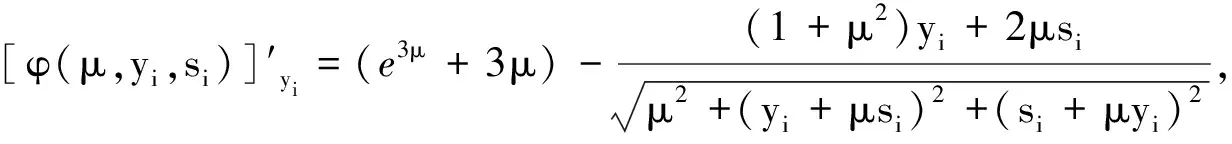
(11)

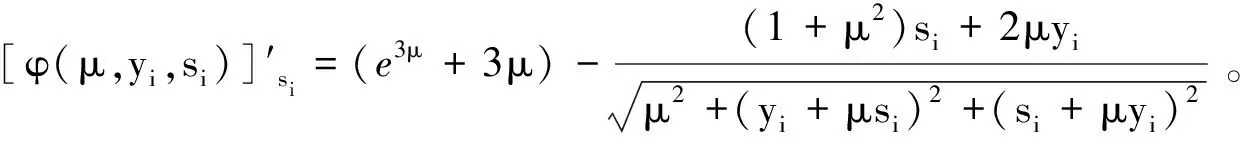
(12)

那么可得，对于任意的i=1,2,…,m，有

0≤[φ(μ,yi,si)]′yi≤e3μ+5μ，0≤[φ(μ,yi,si)]′si≤e3μ+5μ。

引理1设函数H(z)由式(6)定义，则下面结论成立。

1)对于任意的z∶=(μ,x,y,s)∈R++×Rn×Rm×Rm，函数H(z)是连续可微的；

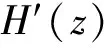
下文中的矩阵A均为列满秩矩阵。

2 非单调Broyden-like算法

本节建立了求解由式(8)定义的方程H(z)=0的非单调Broyden-like算法。 定义价值函数：

f(z)=||H(z)||。

(13)

显然，有f(z)=0⟺x是VI(X,F)的解。

下面给出算法的具体步骤。

算法1(解VI(X,F)的非单调Broyden-like算法)

步骤2 若f(zk)=0，算法结束；否则，计算

βk∶=β(zk)=γmin{1,f(zk)2},

(14)

并求解下列方程组：

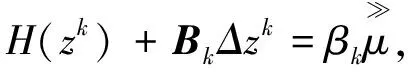
(15)

得向量组Δzk， 其中Bk为由式(9)定义的H(zk)的近似矩阵。

步骤3 若不等式

f(zk+Δzk)≤αf(zk)-σ||Δzk||2，

(16)

成立，令λk∶=1且转步骤5。

步骤4mk为使得下式成立的最小非负整数m，

f(zk+δmΔzk)≤Ck-σ1‖δmΔzk‖2-σ2δmf(zk),

(17)

则令λk=δmk,其中

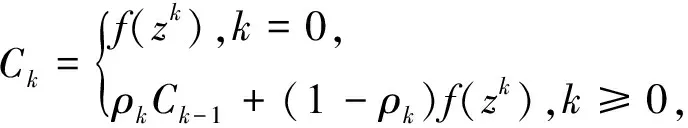
(18)

且ρk∈[ρmin,ρmax],转步骤5。

步骤5 令zk+1:=zk+λkΔzk。

步骤6 更新Bk得到Bk+1

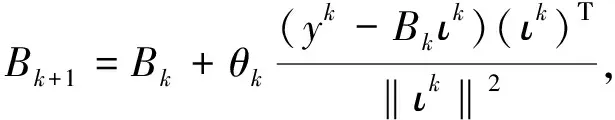
(19)

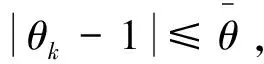
注：非单调线搜索式(17)由Gu和Mo在文献[8]首次给出，式(18)中若ρk=0，那么非单调线搜索转化为文献[9]中提出的单调线搜索。

引理2算法1是适定的。即对于所有的k≥0，必存在一个非负整数mk使得非单调线搜索式(17)成立。

证明 当λk→0+时，显然有f(zk)≤Ck。

由C0的定义，可知当k=0时结论成立。 假设f(zk)≤Ck，下面证明f(zk+1)≤Ck+1。 下面分两种情况进行讨论。

情况一 若式(16)成立，那么f(zk+Δzk)≤αf(zk)≤f(zk)≤Ck。

情况二 若算法1运行了式(17)，那么f(zk+1)≤Ck-σ1||λkΔzk||2-σ2f(zk)≤Ck。

那么，可得式f(zk+1)≤Ck成立，结合式(18)，可得

f(zk+1)-Ck+1=ρk+1(f(zk+1)-Ck)≤0。

(20)

综上可得，对于任意的k≥0有f(zk)≤Ck。 证毕。

由引理2，可得：

推论1 若序列{zk}由算法1迭代生成，那么对于任意的k≥0，有

f(zk)≤Ck。

(21)

引理3设H(·)以及β(·)分别由式(6)和式(14)定义，那么

证明参见文献[10]引理5。

3 收敛性分析

本节讨论算法1的全局收敛性和局部超线性/二次收敛性。 为了分析算法1的收敛性，给出下述假设：

假设1

1)水平集Ω={z∈R++×Rn×Rm×Rm|f(z)≤f(z0)}有界；

2)矩阵H′(z)在集合Ω中是Lipschitz连续的，即存在常数l>0使得

||H′(z1)-H′(z2)||≤l||z1-z2||,∀z1,z2∈Ω；

3)对于任意的z∈Ω，矩阵H′(z)为非奇异矩阵。

引理4设序列{zk}由算法1迭代生成，那么序列{Ck}是非增单调的，且{zk}⊂Ω。

证明参见文献[10]引理6。

引理5若假设1成立，设序列{zk}为由算法1迭代生成的序列，那么

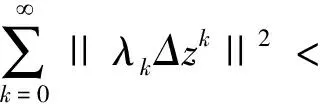
方便起见，定义

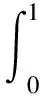
(22)

那么，有yk=Ak+1ιk，其中yk=H(zk+1)-H(zk)且ιk=λkΔzk。 由Bk+1的更新公式，有

(23)

更进一步，令

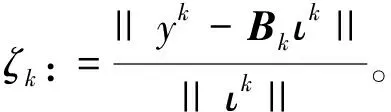
(24)

那么，

(25)

下面的引理来源于文献[11]的引理2.6。

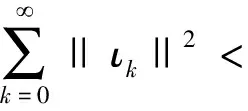
那么

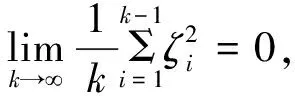
(26)

特别地，序列{ζk}的一个子列趋于0。 此外，若

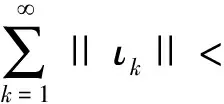
(27)

那么

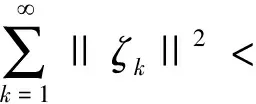
(28)

特别地，整个序列{ζk}收敛于0。

定理1若假设1成立，序列{zk}由算法1迭代生成，那么序列{zk}的任意聚点都是方程(8)的解。

证明由假设1和引理4，可知序列{zk}有界。 不失一般性，假设序列{zk}收敛于序列{zk}的聚点z*。 那么，可以得到z*满足等式f(z*)=0。 随后分两种情况进行讨论：

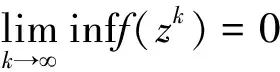
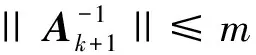
即对于所有充分大的k∈K，存在常数m1>0，有

||Δzk||≤m1f(zk)，

(29)

成立。 不妨设序列{Δzk}k∈K收敛于Δz*=(Δμ*,Δx*,Δy*,Δs*)，由式(25)，可得||(Ak+1-Bk)Δzk||=ζk||Δzk||。 对于k∈K，令k→，可得BkΔzk→H′(z*)Δz*。 另一方面，对于k∈K，令等式(15)两边k→，可得

H(z*)+H′(z*)Δz*=β(z*)μ*。

(30)

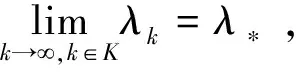
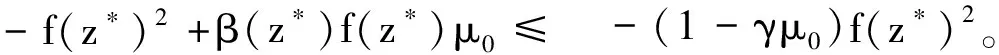
(31)

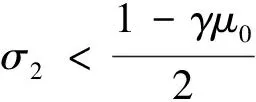
引理7[10]设函数F:Rn→Rn是局部Lipschitz函数，那么

1)类似于Clarke[12]，函数F有广义雅克比 ∂F(x)。 且若函数F在点x处半光滑，则在点x沿着方向h∈Rn函数F的方向导数F′(x;h)存在。 另外，函数F在点x∈Rn处半光滑等价于其所有的分量函数在点x∈Rn处半光滑。

2)函数F在点x处半光滑，当且仅当对于所有的V∈∂F(x+h),h→0，有

||Vh-F′(x:h)||=o(||h||)。

另外，||F(x+h)-F(x)-F′(x:h)||=o(||h||)。

3)函数F在点x处强半光滑等价于对于所有的V∈∂F(x+h),h→0，有

||Vh-F′(x;h)||=O(||h||2)。

另外，||F(x+h)-F(x)-F′(x:h)||=O(||h||2)。

引理8[10]令函数H和函数Θ分别由式(6)和式(7)定义，那么

1)函数Θ是半光滑的。

2)函数H是局部Lipschitz和半光滑的，更进一步，若函数F′(x)Lipschitz连续，那么，函数H是强半光滑的。

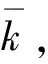
f(zk+Δzk)<αf(zk)-σ||Δzk||2,

(32)

成立。

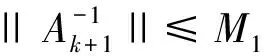
||Δzk||≤M2f(zk)。

(33)

成立。 由函数H的半光滑性，对于任意的充分逼近于z*的zk，存在正常数L1，使得

f(zk)=||H(zk)-H(z*)||≤L1||zk-z*||，

(34)

成立。 另一方面，由H′(z*)的非奇异性以及序列{zk}收敛于z*，存在常数L2>0，使得

f(zk)=||H(zk)-H(z*)||≥L2||zk-z*||，

(35)

成立。 由式(34)和式(35)，有

o(||zk-z*||)=o(||H(zk)-H(z*)||)=o(||H(zk)||)。

(36)

由式(33)和式(34)，可得

||Δzk||≤M2||H(zk)-H(z*)||≤M2L1||zk-z*||。

(37)

由式(15)，得

(Ak+1-H′(zk))(zk-z*)+(Ak+1-Bk)Δzk-[H(zk)-H(z*)-H′(zk)(zk-z*)]。

那么，得

||zk+Δzk-z*||≤M1(ζkM2f(zk)+γμ0f(zk)2+o(||zk-z*||))≤

M1(ζkM2L1||zk-z*||+o(||zk-z*||))。

(38)

那么，当zk充分逼近于z*时，得

f(zk+Δzk)≤||H(zk+Δzk)-H(z*)||≤L1||zk+Δzk-z*||≤

M3ζk||zk-z*||+o(||zk-z*||)。

(39)

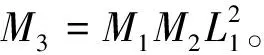
f(zk+Δzk)-αf(zk)+σ||Δzk||2≤M3ζk||zk-z*||+o(||zk-z*||)-αL2||zk-z*||+

(40)

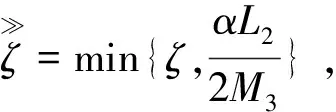
由此可得，当zk充分逼近于z*时，有λk=1满足式(31)。

下面分析算法1的局部超线性收敛性。

定理2若假设1成立，序列{zk}由算法1迭代生成，且z*为{zk}的聚点，那么，序列{zk}超线性收敛于z*，即||zk+1-z*||=o(||zk-z*||)。

(41)

由式(35)，得

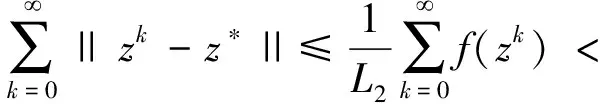
(42)

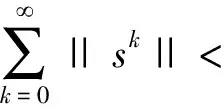
由引理6，可得，当k→时，ζk→0。

下面给出算法1的局部二次收敛性。

定理3设假设1成立，若所有的V∈∂H(z*)都是非奇异的，对于任意的x∈Rn函数F′(x)Lipschitz连续，那么，由算法1生成的序列{zk}二次收敛于VI(X,F)的解z*=(0,x*,y*,s*)，即||zk+1-z*||=O(||zk-z*||2)。

证明类似于文献[13]的定理5.2。

4 结语

讨论了一类变分不等式问题，基于Fischer-Burmeister函数，建立了求解变分不等式问题的非单调Broyden-like算法，并证明的算法的全局收敛性以及局部超线性/二次收敛性。