一类新零差分平衡函数的构造及应用
2019-11-14
(1.福建船政交通职业学院公共教学部, 福建 福州 350007; 2.福建工贸学校, 福建 福州 350002)
设A和B分别是阶为n和l的两个加法群。令f是从A到B的一个映射, 定义Da(x)=f(x+a)-f(x)。若存在一个非负整数λ,使得对每个非零a∈A有|x∈A:Da(x)=0|=λ成立, 则称f是一个零差分平衡函数(简记,ZDB函数)。 函数f亦称作是一个(n,l,λ)-ZDB函数, 其中l表示f的象集的大小。
2013年蔡晗等人基于Zeng-Cai-Tang分圆构造出参数为(n,(n+e-1)∕e,e-1)的ZDB函数, 其中n是大于3的奇数并设n=pm11pm22…pmkk[1]。 最近, 蔡晗在之前工作的基础上, 巧妙地运用中国剩余定理又构造出一类新的ZDB函数[2]。 2013年, 丁存生等人构造出三类新的ZDB函数[3]。 基于丁存生教授在二阶分圆陪集的这个想法, 查正邦和胡磊给出ZDB函数的一些分圆构造[4]。 2015年, 柯品惠和叶智钒等人基于费马商给出p2到p的ZDB函数一般构造[5-6]。 2017年, Su从差平衡函数和最佳三元序列构造出两类具有新参数ZDB函数[7]。
1 分圆类
1.1 二阶分圆类
设m=2e-1。存在一个最小正整数la使得a≡a2la(modm), 记
A(a,la)={a,a×2(modm),a×22(modm),…,a×2la-1(modm)}⊆m
则A(a,la)是模m包含a的一个二阶分圆陪集。其中最小的正整数la和陪集A(a,la)里的最小正整数分别称作这个分圆陪集的大小和陪集首。
若e是一个素数, 则模m的每个非零二阶分圆陪集的大小为e, 即la=e。 令A(a,2e)={A(a,e)∪-A(a,e)}, 其中-A(a,e)={m-1|i∈A(a,e)}, 且A(a,2e)的个数为(2e-1-1)/e。 不妨把A(a,2e)最小的正整数仍称为陪集首, 且陪集首a是唯一的。设A0={0}, 把所有A(a,2e)排成一行放置, 第j个陪集记为A(a,2e)j,1≤j≤(2e-1-1)/e。对任意1≤j≠j′≤(2e-1-1)/e, 有下列划分:
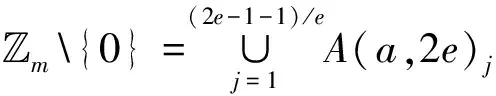
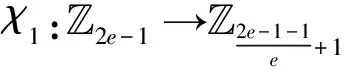

(1)
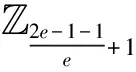
引理1[3]对任意元素τ∈2e-1{0}, 那么有
1.2 Zeng-Cai-Tang广义分圆类
对于元素a和*n的子集D, 定义a+D和aD如下:a+D={a+d|d∈D},aD={ad|d∈D}, 其中加法和乘法运算是在模n下进行的。
对任意给定一个奇数n≥3, 由唯一分解定理,n能表示成pm11pm22…pmkk的形式, 其中pi是奇素数且mi是正整数对任意1≤i≤k。 在本文中对任意1≤i≠j≤k, 总是令pi≠pj。对每个整数1≤i≤k, 存在gi使得gi是模pmii的一个本原根对所有mi≥1。 记φ(x)为欧拉函数表示小于等于x并与x互素的个数, 则gi模pmii的乘法阶为φ(pmii)=pmi-1i(pi-1)。对任意1≤i≤k, 设2e|pi-1, 即存在k个fi使得pi-1=2efi。由中国剩余定理, 对每个1≤j≤k和1≤i≤k, 都存在唯一hj∈*n使得
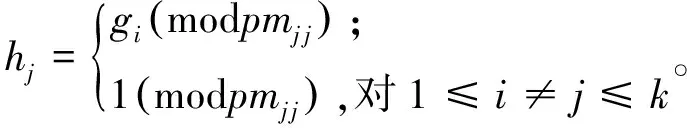
(2)
设n1≥3是n的一个因子且记π(n1)表示n1的不同素因子的个数, 则存在π(n1)个数t1,t1,…,tπ(n1)∈{1,2,…,k}和π(n1)个数m′t1,m′t2,…,m′tπ(n1)使得
n1=pm′t1t1pm′t2t2…pm′tπ(n1)tπ(n1),
其中1≤m′t≤mt对t∈T={t1,t1,…,tπ(n1)}⊆{1,2,…,k}。再次用中国剩余定理, 对每个t∈T, 可知存在唯一g(n1,2e)∈*n1有g(n1,2e)=gftpm′t-1tt(modpm′tt)。显然地,g(n1,2e)模n1的乘法阶为2e且集合D(n1,2e)={gi(n1,2e)|0≤i≤2e-1}是*n1的一个阶为2e的循环子群[8]。
对每个t∈T, 设lt=φ(pm′tt)=pm′t-1t(pt-1)且定义一个集合ψ(2e)n1为ψ(2e)n1={j∈lt1|0≤j≤ftpm′t-1t-1}×lt2×…×ltπ(n1)。对任意In1=(i1,i2,,inπ(n1))∈ψ(2e)n1, 定义D(n1,2e)In1为D(n1,2e)In1=HIn1n1D(n1,2e), 其中Hn1=ht1ht2…htπ(n1)且定义HIn1n1为
HIn1n1=hi1t1hi1t1…hiπ(n1)tπ(n1)(modn1)。
特别地,D(n1,2e)O=D(n1,2e), 这里O表示π(n1)维零向量。文献[11]证明了{D(n1,2e)In1|In1∈ψ(2e)n1} 是*n1的一个划分,D(n1,2e)In1被称作阶为关于n1的广义分圆类。 那么, 可得到n的一个如下划分:
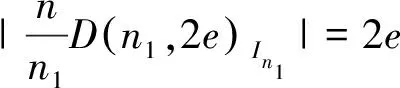
2 ZDB 函数的新构造
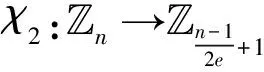
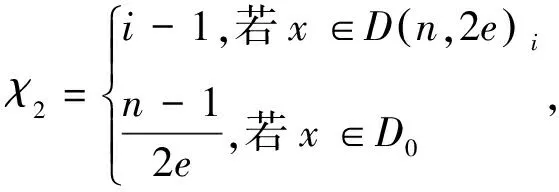
(3)
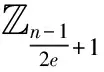
引理2对任意元素τ∈n{0}, 那么有
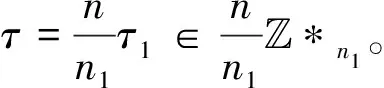
倒数第三个等式成立, 由于I跑遍所有ψ(2e)n1时, 有τ1D(n1,2e)I=τ1*n1=*n1。 最后一个等式成立, 因为在D(n1,2e)O中除了0, 其他2e-1个元素均属于*n1。
下列定理可由引理2直接得到。
定理1函数χ2(·)是构造1中定义的函数, 那么它是从n到的一个函数。
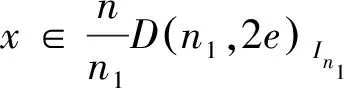
θ(x)=(ix)2e,
(4)
其中, (ix)2e表示ix模2e同余的最小非负整数, 则θ(x)是n{0}到集合{0,1,…,2e-1}的一个函数。
引理3[4]若任意给定正整数τ具有τ0=(τ)2e≠0且τ2=(τ)n≠0, 则有唯一的
使得τ0+θ((x+τ2)n)≡θ(x)(mod 2e), 其中θ(x)为式(4)所定义的函数。
若x∈A(a,2e)j, 定义
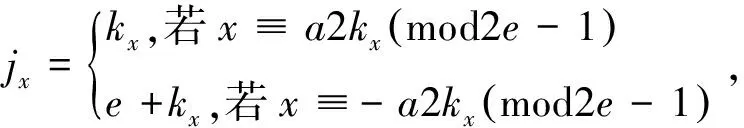
(5)
且
η(x)=(jx)2e,
(6)
其中,i≤j≤(2e-1-1)/e,a表示是在集合A(a,2e)中最小的正整数值且(jx)2e表示jx模2e同余的最小非负整数, 则η(x)是2e-1到集合{0,1,…,2e-1}的一个函数。
引理4对任意给定整数τ1,τ2, 其中τ1∈2e-1τ2≤2e-1。 若x∈A(a,2e)j, 对每个jx, 0≤jx≤ 2e-1有唯一的(a,jx), 使得τ1+(jx+τ2)-1≡j-1x(mod2e-1)。
证明:因为e是一个素数, 对任意1≤τ0≤e-1, 有gcd(2τ0-1,2e-1)=2gcd (τ0,e)-1=1。对任意陪集首a和1≤τ0≤e-1, 则有a2i-a2i+τ0∈2e-1{0}对0≤i≤e-1。另一方面, 若存在两个二阶分圆陪集首a,b和两个整数0≤i1,i2≤e-1, 使得τ1±2i1+τ0≡±a2i1(mod 2e-1)且τ1±b2i2+τ0≡±a2i1(mod 2e-1),则有
τ1≡±a2i1(1-2τ0)(mod2e-1)≡±b2i2(1-2τ0)(mod2e-1)。
由gcd(2τ0-1,2e-1)=1, 可得a2i1≡±b2i2(mod 2e-1), 从而a=±b和i1=i2。因为陪集首的个数为(2e-1-1)/e且1≤jx≤2e-1, 因此τ1+(jx+τ2)-1≡j-1x(mod 2e-1)有唯一解(a,jx)。证毕。
下列推论可以直接从引理4得到。
推论1若任意给定正整数τ, 若τ0=(τ)2e≠0且τ1=(τ)2e-1≠0, 则有唯一的
使得τ0+η((x+τ1)2e-1)≡η(x)(mod 2e), 其中η(x)为式(6)所定义的函数。
以下介绍ZDB函数的构造。
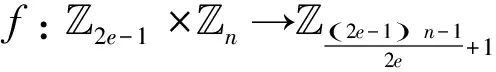

(7)
这里t1=(t)2e-1和t2=(t)n, 且χ1和χ2分别为式(1)和式(3)所定义。
通过χ1和χ2的定义, 容易知道如下结论成立。
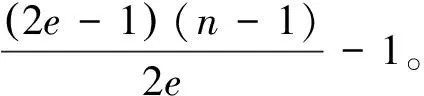
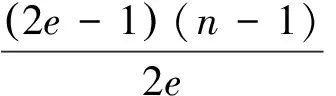
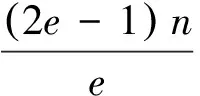
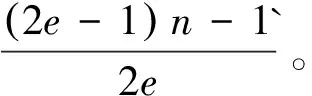
因此, 函数f的定义是合理的而且是从2e-1×n到的满射。对任意和有|D(n,2e)i|=|A(a,2e)j|=2e。 因此f的原象分布为{1,2e,2e,…,2e}, 这里1对应的情形。下列定理是本文的主要结果:
定理2函数f是构造2中定义的函数, 那么它是从2e-1×n到的一个函数。
证明: 对任意给定τ=(τ1,τ2)≠(0,0),τ1∈2e-1且τ2∈n, 定义
Δ1(τ)=|{t∈2e-1×n|f(t+τ)=f(t),t1≠0,t2=0}|
和
Δ2(τ)=|{t∈2e-1×n|f(t+τ)=f(t),t1≠0,t2≠0}|,
由文献[9]的引理3.1.6和引理3.1.7可知

(8)

(9)
那么, 有|{t∈2e-1×n|f(t+τ)-f(t)=0}|=Δ1(τ)+Δ2(τ)+Δ3(τ),其中, 定义Δ3(τ)=|{t∈2e-1×n|f(t+τ)=f(t),t1≠0,t2≠0}|。类似文献[8]引理3.1.8可证明

(10)
因此, 对τ≠(0,0), 有|{t∈(2e-1)n|f(t+τ)-f(t)=0}|=2e-1。证毕。
例子设n=p1=13,e=3,m=7且2是模13的本原元。 那么, 广义分圆类如下:
D(13,6)1={1,4,3,12,9,10},D(13,6)2={2,8,6,11,5,7},D0={0}。
又模7的二阶分圆陪集为A(1,6)1={1,2,4,6,5,3},A0={0}。
定义
和
通过构造2, 能得到一个函数f(t)。 具体地,f(t)值如下
(f(0),f(1),…,f(90))=(15, 0, 7, 1, 3, 8, 11, 14, 7, 5, 4, 11, 1, 12, 13, 6, 3, 0, 6, 6, 8, 14,4, 0,8, 5, 12, 3, 14, 2, 2, 9, 10, 9, 10, 13, 5, 10, 2, 12, 4, 9, 13, 1, 11, 7, 7,11, 1,13, 9, 4, 12,2, 10, 5, 13, 10, 9, 10, 9, 2, 2, 14, 3, 12, 5, 8, 0, 4,14, 8, 6, 6, 0, 3, 6, 13, 12, 1, 11, 4, 5, 7, 14, 11, 8, 3, 1, 7, 0)。
由Magama, 容易验证对任意1≤τ≤90, 有|{t|f(t+τ)=f(t)=0,1≤t≤90}|=5。因此,f是一个从91到91(91,16,5)-ZDB函数。
3 零查分平衡函数在最佳跳频序列的应用举例
ZDB函数主要有三方面的应用:常重复合码(CCC), 集合差系统(DSS)和跳频序列(FHS), 本文只给出该构造在跳频序列中的具体应用。
例如,设F={f0,f0,…,fl-1}是一个频率集, 亦称其为字母表。若xt∈F对0≤t≤N-1, 则称X={xt}N-1t=0为一个长度为N的跳频序列(FHS)。
对一个F上长度N的跳频序列X={xt}N-1t=0, 它的周期汉明自相关HX定义为
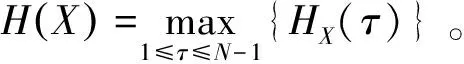
设|F|=l,F上的序列周期为N, 最大周期汉明自相关为λ, 记该跳频序列为(N,l,λ)FHS. Lempel和Greenberger给出了如下关于最大周期汉明自相关的一个理论下界:
引理5[1](L-G界)设X是一个(N,l,λ)-FHS, 则有
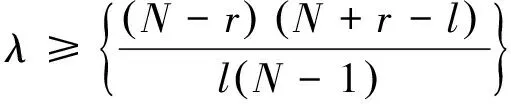
(11)
其中,r是满足N≡r(modl)最小的非负整数, 且「t⎤表示大于或等于t的最小整数。
最近, 文献[1]给出了FHS和ZDB函数之间的一个关系刻画。
引理6若f是一个(N,l,λ)-ZDB函数从一个循环群A到阿贝尔群B,按如下方式定义一个长度N=|A|的跳频序列S={si}N-1i=0, 其中si=f(αi), 对 0≤i≤N-1, 且α是A的一个生成元, 则S是在字母表F=Im(f)⊆B上的一个(N,l,λ)FHS。
