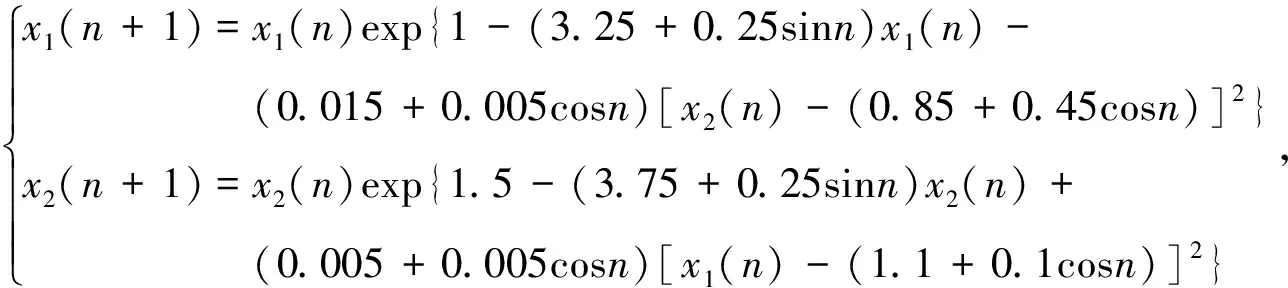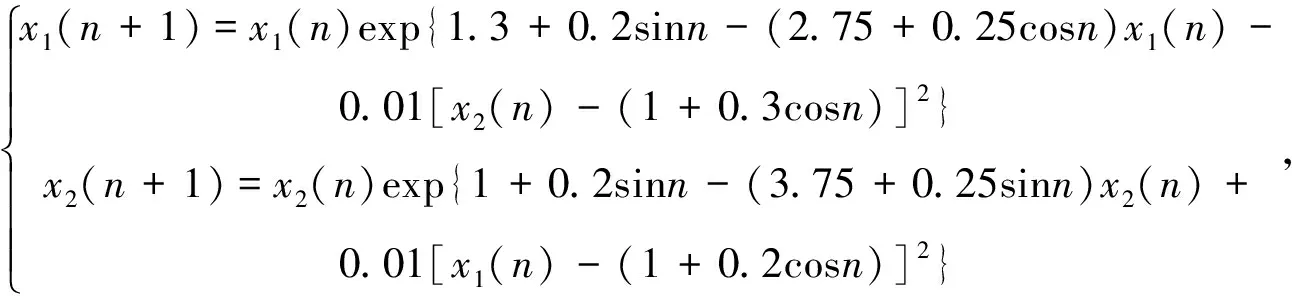一类离散的两企业竞争模型的全局吸引性
2019-11-14吴丽萍
吴丽萍
(闽江学院数学与数据科学学院, 福建 福州 350108)
文[1]提出如下两企业竞争模型
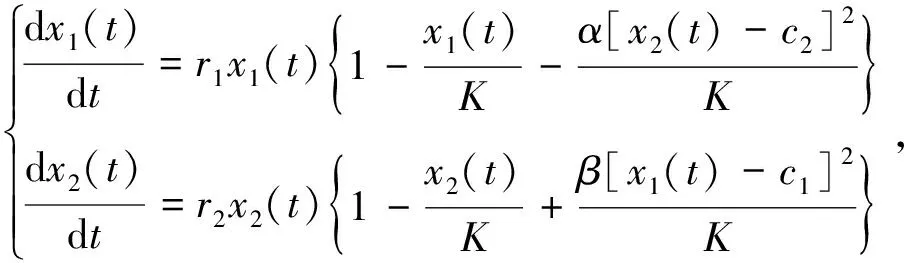
(1)
其中x1(t),x2(t)分别表示企业A和企业B的产出量,r1,r2表示企业产量内禀赋增长率,K表示在无限制条件下的自然市场负载量,α,β表示两企业的竞争系数,c1,c2为两企业的初始生产量。
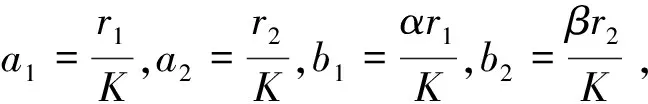
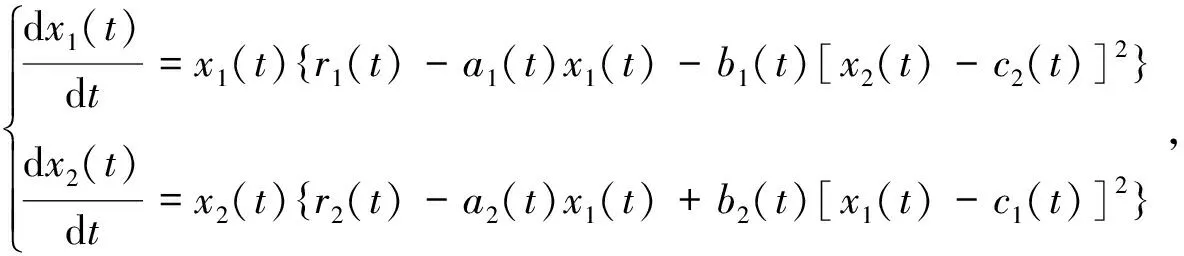
(2)
文[1]运用重合度理论中的连续性定理,得到了模型(2)对应的时标系统存在正周期解的一个充分条件。本文研究系统(2)的离散化模型
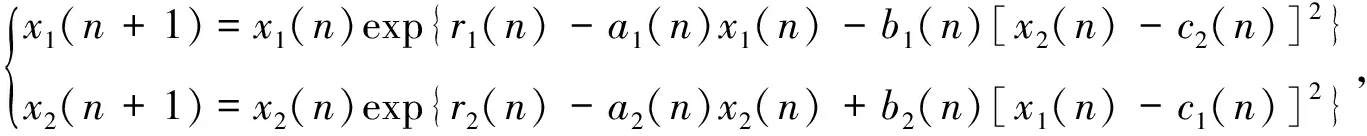
(3)
其中各系数的含义与系统(2)相同。文[2]在假设系统(3)的系数均为周期函数的条件下, 利用重合度理论得到该系统至少存在一个正周期解的充分条件。但文[2]对系统(3)的持久性及全局吸引性均未涉及。然而, 在对生态系统的研究中, 持久性和全局吸引性是一个重要的课题。
近年来, 系统(2)得到广泛研究, 见文[3-6]及其所引文献。但尚未有文献对系统(3)的持久性和全局吸引性进行研究。本文的目的在于研究系统(3)的持久性和全局吸引性。
在本文中, 假设ri(n),ai(n),bi(n),ci(n)(i=1,2)为非负有界序列, 且
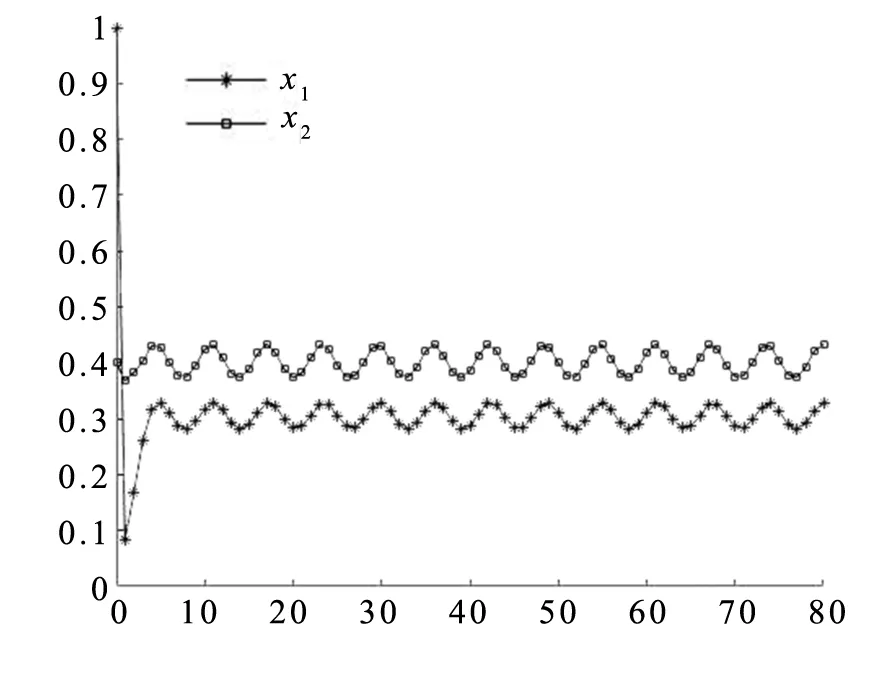
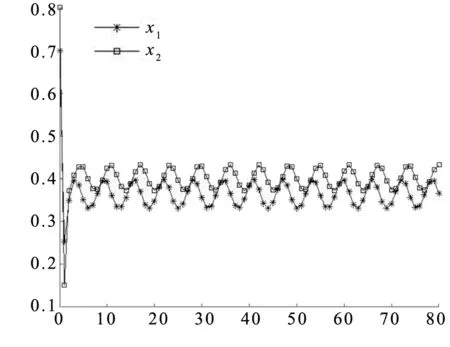
0 这里对任一有界序列{g(n)},gu=supn∈g(n),gl=infn∈g(n), 其中表示非负整数集。 基于生态学意义, 本文考虑系统(3)具有正初值x1(0)>0,x2(0)>0的解 (x1(n),x2(n))。易知, 系统(3)具有正初值的解是正的。 引理1[7]假设{x(n)} 满足x(n)>0且x(n+1)≤x(n)exp{a(n)-b(n)x(n)},n∈, 引理2[7]假设{x(n)} 满足x(n)>0且 其中{a(n)}和{b(n)} 是有正的上界和下界的序列,N0∈, 则 引理3对系统(3)的任一正解(x1(n),x2(n)), 有 (4) 注: 引理3的证明与文[8]中引理 5证明类似, 此处略去。 (5) 证明由(H1)知存在充分小的正数ε,使得 由引理3, 对上述ε>0, ∃n1∈+,当n>n1时, 有xi(n) 从而由系统(3)的第一个方程, 当n>n1时, 有 由引理2, 得 由系统(3)的第二个方程可得, 当n>n1时, 有 x2(n+1)≥x2(n)exp{r2(n)-a2(n)x2(n)-2b2(n)c1(n)x1(n)}≥ 由引理3和引理4即得 定理1设系统(3)满足引理4中的条件(H1) , 则系统(3)是持久的。 定理2假设定理1的条件成立, 进一步假设 (6) 由微分中值定理知,exp{ui(n)}-1=exp{θi(n)ui(n)}ui(n),θi(n)∈(0,1),i=1,2。 所以式(6)可化为 (7) 由已知条件, 可选取充分小的ε(0<ε 由定理1, 对上述ε, ∃n2∈+,当n>n2时, 有 于是由式(7)的第一式得, 当n>n2时, 有 (8) 类似可由式(7)的第二式得, 当n>n2时, 有 (9) 记λ=max{λ1ε,λ2ε},则0<λ<1。由式(8)和式(9)得, 当n>n2时, 有 max{u1(n+1),u2(n+1)}≤λmax{u1(n),u2(n)}。 从而可得 max{u1(n),u2(n)}≤λn-n2max{u1(n2),u2(n2)}。 即系统(3)是全局吸引的。 例1考虑如下例子 (10) 计算可得A1≈0.962>0,A2≈1.492>0,λ1≈0.362<1,λ2≈0.942<1.所以系统(10)满足定理2的条件,从而是全局吸引的。系统(10)具有初值(x1(0),x2(0))=(1.0,0.4)的解的数值模拟, 如图1所示。 例2 考虑如下例子 (11) 计算可得A1≈1.082>0,A2≈0.784>0,λ1≈0.992<1,λ2≈0.672<1。所以系统(11)满足定理2的条件,从而是全局吸引的。系统(11)具有初值(x1(0),x2(0))=(0.7,0.8)的解的数值模拟, 如图2所示。 图1 系统(10)的数值模拟图Fig.1 Dynamics behaviors of system 10 图2 系统(11)的数值模拟图Fig.2 Dynamics behaviors of system 111 持久性
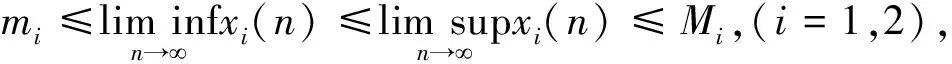
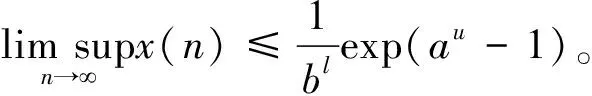

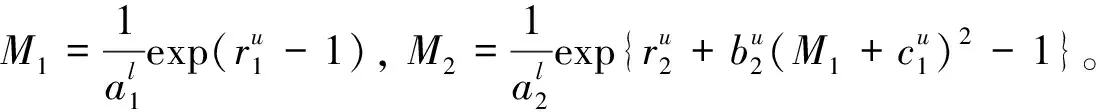
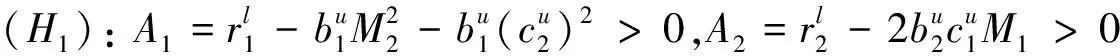
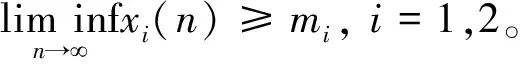
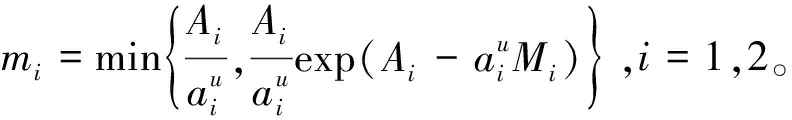
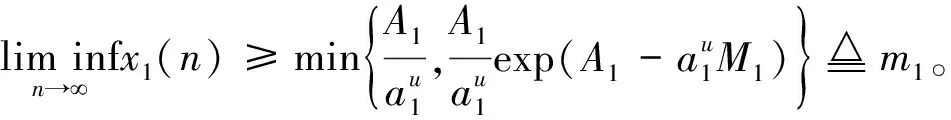
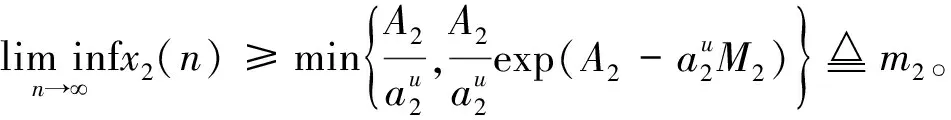
2 全局吸引性
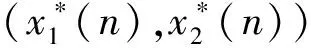
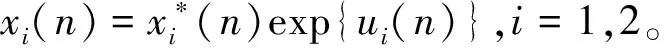
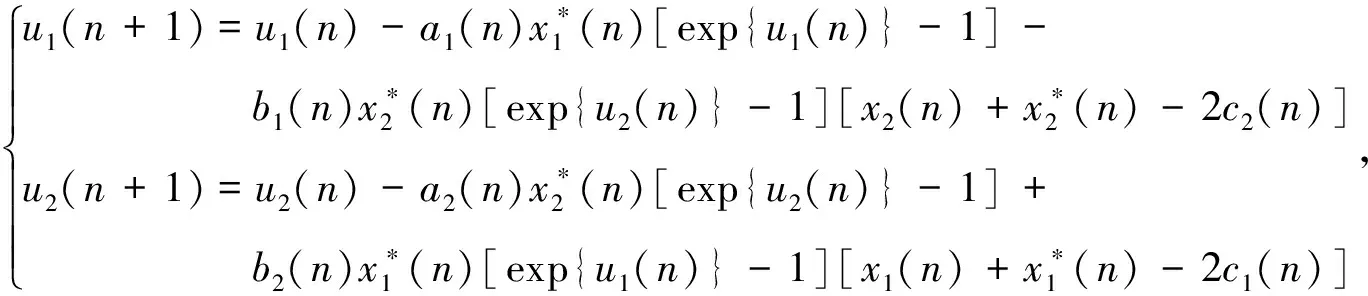
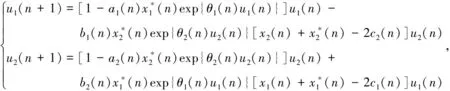
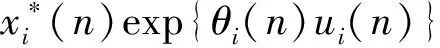
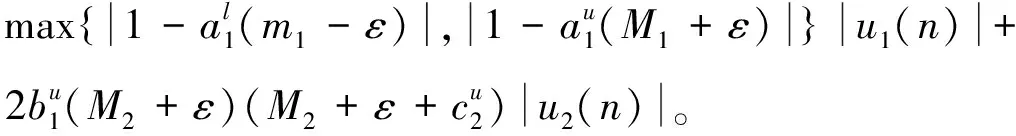
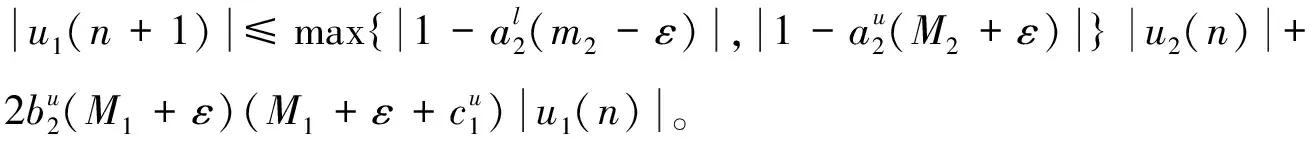
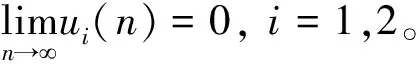
3 例子