STIT 逻辑的能力片段初探
2019-11-14何键枫
何键枫
1 引言
STIT(Seeing To It That)理论提出于20 世纪80 年代,它是研究主体与其行动所致结果之间关系的一类行动逻辑([2,3,11,15,16])。有别于其它以动态逻辑为基础的行动逻辑,STIT 理论并不讨论主体的行动本身,而是聚焦于发挥能动作用的主体之上。形式地说,STIT 理论一般情况下是在命题逻辑的基础上扩充以STIT 算子与历史必然算子而得到的一类模态逻辑。出于不同的分析需求,文献中存在不同的STIT 算子([3,6,7,10])。以语义最为简单的CSTIT 算子为例,公式[i:cstit]φ 的读法为:主体i 的当前行动确保φ 的成立。利用历史可能算子,我们甚至能在STIT 理论的框架下讨论主体的能力问题:公式的读法为主体i 能够确保φ 的成立,其中◇是历史必然算子□的对偶。另一方面,得益于STIT 理论的语义模型特点,我们能够以一种非常自然的方式将个体STIT 算子推广为群体STIT 算子([9]),群体的共同行动(joint action)乃至群体的能力亦能在STIT 理论下得到刻画。
尽管个体STIT 算子能够被非常自然地推广为群体STIT 算子,关于个体STIT 算子的技术结果,如逻辑的可判定性、可靠完全的公理系统等([21,22]),却未能在群体STIT 算子中得以保留。文献[8]将群体STIT 逻辑的公式可满足问题归约为乘积逻辑S5n的公式可满足问题,从而证明了当主体集的基数大于等于3 时,群体STIT 逻辑不可判定且无法有穷公理化。面对上述群体STIT 逻辑的否定性结果,一个自然的思路是放弃整个群体STIT 逻辑,转而考虑STIT逻辑的特殊片段:文献[13]通过严格限制公式的构造,尤其是历史必然算子与群体STIT 算子的叠置,从而得到了群体STIT 逻辑的一个可判定片段以及相应的公理系统;文献[18]则定义了一类由群体构成的格,并且将群体STIT 算子的构造限制在格点上,从而得到了群体STIT 逻辑的又一可判定片段与相应的公理系统;文献[5]讨论了STIT 理论的一个基于时态逻辑的扩充,其中代替CSTIT 算子而新引入的XSTIT 算子(可视作的缩写,其中X 是表示下一刻的明日算子)由于不满足交集性质,同样得到了有穷的公理系统并保持了可判定性;文献[23]通过弱化群组CSTIT 算子的交集性质,得到了基于Z 型STIT 框架且含有直到算子与自从算子的可判定片段。
本文的结构如下:在第2 节中,我们将重点放在STIT 逻辑包含个体的能力片段上,并证明如果只考虑能力片段,每个STIT 模型都存在等价的邻域模型。以此为基础,本文给出一个公理系统,并通过逐步构造法证明其完全性。对STIT 逻辑包含群体的能力片段的讨论则是第3 节的任务,我们利用类似的方法证明包含群体的能力片段的完全性。最后,我们在第4 节中对本文的工作进行总结,并简单讨论将来的研究思路。
2 个体STIT 理论的能力片段
本节讨论STIT 理论中只含个体的能力片段。我们先介绍STIT 理论经典的BT+AC 模型,并证明只考虑能力片段时,每个BT+AC 模型都对应于一个等价的邻域模型。因此,当考虑完全性证明时,本文的策略是为每个一致公式集构造相应的邻域模型。
2.1 语言与语义
预设可数命题变元集PROP 与有穷的非空主体集AGT,并考虑语义最为简单的CSTIT 算子与历史可能算子。下面给出公式的定义:
定义1(公式).公式由以下BNF 递归定义得到:
将上面定义构造的公式称为个体STIT 逻辑的能力片段,本节中公式均为个体STIT 理论的能力片段公式。值得一提的是,当时,历史必然算子□是冗余的,即□φ 逻辑等值于,其中i,j 为不同主体([1])。因此,本文处理的其实是形如的公式。
下面给出STIT 理论的形式语义,STIT 理论的语义框架BT+AC 由两部分构成。其中,BT 是分支时间理论的缩写([17,19,20])。分支时间理论以类树结构表示非决定的世界:向前可分支表示将来未定,向后不分支表示过去唯一。历史是类树结构中的极大链,直观意义为世界的一种可能的完整演变进程。
定义2(分支时间).分支时间结构T=(W,<)是满足下面条件的二元组:
· W 为非空时刻集,<是W 上严格偏序,表示状态的先后关系;
· <满足树状性:对于任意w1与w2,如果w1<w3且w2<w3,那么w1=w2或w1<w2或w2<w1成立;
· <满足历史关联性:对于任意w1与w2,存在w0满足w0≤w1且w0≤w2,其中≤为<的自反闭包。
给定分支时间结构T=(W,<),将历史定义为W 中关于严格偏序<的极大子集h,即任取w,v ∈h 均是关于<可比较的且不存在h 的真超集满足前面条件。将所有历史的集合记作HT并用Hw表示所有穿过状态w 的历史集合,w ∈h 的直观意义为世界在历史h 中曾演变为状态w。给定历史h1,h2∈Hw,如果存在w <w′满足,则称h1与h2在状态w 中未分离。给定历史h与状态w,如果w ∈h,则称序对(w,h)为索引。
STIT 模型的第二部分AC 是将每个主体i 映射到相应选择的Choice 函数,Choice 函数规定了主体在世界中能够作出的选择。Choice 函数的数学定义如下:给定状态w 与主体i,是Hw的分划,主体i 在状态w 的选择正是分划中对应的等价类。上述处理的背后直观为:当世界演变至状态w 时,主体i 的选择c 将会使某些可能的演变进程不再可能,主体i 在状态w 作出选择c的结果是世界之后的演变将局限于c 对应的等价类中。STIT 理论正是将选择带来的结果等同于选择本身。特别地,Choice 函数还需满足两个额外条件:首先,要保证未分离历史是不可区分的,即如果h1与h2在w 上未分离,h1与h2属于中的相同等价类。其次,要保证主体之间是相互独立的,即对于所有状态w、所有主体i 与对应选择,均有并非空集。其中,是中等价类,即主体i 在时刻w 中可作的选择。
定义3(经典STIT 模型).经典STIT 模型M=(W,<,Choice,V)是满足下列条件的四元组:
下面给出基于经典STIT 模型的形式语义。需注意对应的点模型是索引,而非分支时间结构中的状态。
定义4(满足).给定模型M=(W,<,Choice,V)与索引(w,h),称(w,h)满足φ当且仅当:
定义5(邻域STIT 模型).邻域STIT 模型是满足条件的三元组(W,{σi:i ∈AGT},V):
· W 是非空状态集;
-对于任意w,v ∈W 均有σi(w)=σi(v)2之所以要求所有点都必须具有相同的i 邻域,是因为i 邻域对应主体i 能作出的选择。;
-对于任意w ∈W 均有σi(w)是W 上的分划;
在邻域STIT 模型中递归定义公式的满足,特别地对于公式,定义当且仅当存在满足任意u ∈U 均有成立。值得一提的是,本文采用的邻域语义与经典邻域语义存在细微区别:经典邻域语义只有在邻域框架满足单调性时,语义才具备存在-任意特点。另一方面,注意到这个定义与经典STIT 模型下定义的相似之处,事实上,我们有以下结果:
命题1.公式在经典STIT 模型上可满足当且仅当其在邻域STIT 模型上可满足。
推论1.个体STIT 理论的能力片段是可判定的。
同样地,容易得到个体STIT 理论能力片段的复杂度上限:已知不含时态算子的个体STIT 理论在时是NEXPTIME 完全的([1]),相同条件下个体STIT 理论能力片段的可满足问题最坏是在确定型图灵机中指数时间内可检验的。最后,我们在下面给出个体STIT 理论能力片段的一个公理系统。
定义6.表1 与表2 的公理模式与推理规则构成希尔伯特式公理系统ABI.I。

表1:ABI.I 的公理模式

表2:ABI.I 的推理规则
命题2(可靠性).公理系统ABI.I 是可靠的。
2.2 完全性结果
我们证明上节给出的公理系统的完全性,即证明一致的公式集都是可满足的。具体的思路是为一致公式集构造出满足的邻域STIT 模型。由于典范模型无法保证典范邻域函数恰好给出论域的分划(关于邻域语义的典范模型可参考文献[14]),本文的策略为通过逐步构造进行逼近,从而在极限条件下得到所需模型。逐步构造法中使用的概念如网络、融贯性与饱和性等,参考文献[4]。
预设AGT={1,...,k}并给出网络的定义,其中关于极大一致集的定义与性质可参考文献[4]。
定义7(网络).网络是三元组,满足以下条件:
· 标签函数ρ 将任意s ∈S 映射到某个极大一致集。
定义8(融贯性).网络µ=(S,{σi:0 ≤i ≤k},ρ)是融贯的当且仅当3不难发现,条件C1-3 分别对应邻域STIT 框架的相关条件,条件C4 则对应邻域STIT 模型上的语义特点,即:存在s 满足M,= 当且仅当对于任意s 均有M,s|=。:
当网络µ 满足融贯条件C1 时,µ 的可数性将保证µ 拥有可数邻域。
定义9(饱和性).网络是饱和的当且仅当对于任意公式φ,如果存在s ∈S 与i 符合0 ≤i ≤k 满足,则对于任意均存在u ∈U 满足φ ∈ρ(u)。
如果网络是融贯饱和的,称该网络是完美的。给定一个完美网络µ,定义赋值函数并称对应模型Mµ为网络µ 生成的模型。施归纳于公式的结构容易证明下面引理。
引理1(真值引理).令µ 为可数无穷的完美网络,对于任意公式φ 与任意s ∈S,满足:Mµ,s|=φ 当且仅当φ ∈ρ(s)。
根据上面引理,给定一致公式集φ 并将其扩充为极大一致集,只需要构造完美网络满足存在s ∈S 使得Φ ⊆ρ(s),我们便能得到相应的模型。另一方面,完美网络可以在融贯网络的基础上,通过逐步移除融贯网络中不满足饱和要求的反例,从而在极限条件下定义出来。
定义10(缺陷).令为融贯网络,公式为µ 中缺陷当且仅当存在s ∈S 与U ∈σi(s)满足任意u ∈U 均有φρ(u)。
给定融贯网络µ 与µ 中缺陷D,我们可以通过扩充网络的方式修补缺陷。但是,由于任意地向邻域添加元素可能会破坏融贯条件C5,我们引入基于网络µ 与公式集Γ 的辅助函数λ。下面给出辅助函数λ 与网络扩充的严格定义:
定义11(辅助函数).λ 是基于与Γ 的辅助函数当且仅当:
定义12(扩充).给定网络称µ′是µ 的扩充当且仅当:
引理2.令Φ 为极大一致集,存在融贯网络与基于µ以及的辅助函数λ,其中存在s ∈S 且ρ(s)=Φ。特别地,µ 是可数网络。
将{0,...,j-1}记作AGT′,将AGT′关于的补集记作AGT′′,对于任意i ∈AGT′,辅助函数λjn保证了存在单射非满射函数为相应能力公式指派证据邻域。令。尽管W 在严格意义上并非子集,它显然唯一对应于的某个子集,因此不会引起混淆。将记作V。
给定序对(w1,w2)∈W,它对应于某个合取。我们在前面已经验证过∪ 的一致性,将其扩充为极大一致集并记作Γ(w1)。引入个新点并将这些新点标签为Γ(w1)。即,对于任意,引入新点s(w1,w2)并将其标签为Γ(w1)。将引入的新点集记作S(w1)并注意到。对于任意并非空集当且仅当。
其中,
现在验证µjn+1是否为满足C1-C4 的可数网络。根据选择公理可知可数个可数集合的并集依然可数,故S′可数且对于i≠j 有。此外,依然可数。令为新构造的邻域,则U为的证据。任取,则显然存在与x 一一对应。如果,显然有∩并非空集。如果x′∈V,则存在使得,再次得到∩并非空集。
由上可知我们完成了对µjn+1的定义,我们还需要定义辅助函数λjn+1。然而,λjn+1的定义是显然的:对于任意i 符合0 ≤i ≤j-1 以及,定义为在µjn+1中的扩充;对于任意,定义;令中新增邻域,定义。上面的构造保证了我们对λjn+1的定义是成功的且相对于λjn合适。
对于任意i 符合0 ≤i ≤k,称Sj+1的子集构成的可数序列{An:n ∈ω}是关于i的邻域链,如果该序列满足:第一,{An:n ∈ω}是非降序列;第二,存在m ∈ω满足任意n ∈ω 均有4特别地,如果m=0,此时默认Sjm-1为空集。;第三,如果则相交为空。定义为:
不难验证µ 是满足C1-C4 的可数网络:S 是可数个可数集合的并,因此是可数的;对于融贯性,只验证融贯条件C1,假设s′∈S 则存在最小的n 满足s′∈Sjn。注意到是对Sjn的分划,因此存在满足。不难找到邻域链I 满足。另一方面,容易验证给定关于j的邻域链I,I′,则有∪I=∪I′当且仅当I=I′。因此是Sj+1上分划。
现在只剩下定义出满足条件的基于µj+1与的辅助函数λj+1。对于任意i 符合,定义为包含的关于i 的邻域链的并集,辅助函数序列λj0,...,λjn,...保证了任意均有成立;对于任意n ∈ω,定义为包含的关于j 的邻域链的并集。辅助函数序列λj0,...,λjn,...保证了任意均有成立。关于辅助函数的其他要求显然满足。
因此,我们成功定义了满足条件的网络µj+1与辅助函数λj+1。注意到AGT 是有穷的,只需要将以上的步骤重复有穷多次,便可得到一个可数融贯网络以及基于µ 以及的辅助函数λ,其中。
引理3(修补引理).令为可数融贯网络且λ 为基于µ以及的辅助函数,其中s ∈S 成立。假设D 为µ 中缺陷。存在µ 的一个可数融贯扩充且基于µ′的辅助函数λ′满足λ′相对于λ 合适。特别地,D 并非µ′中缺陷。
其中,
不难验证µ′是µ 的可数融贯扩充,并非其中缺陷。µ′并没有增加邻域,而我们对原有邻域中新增的点并不会破坏融贯条件C5。对于辅助函数λ′的定义是显然的:对于任意i 符合0 ≤i ≤k 以及,只需定义为λ在µ′的扩充。λ′显然是相对于λ 合适的。
命题3(完全性).一致公式集都是可满足的。
对于任意i 符合0 ≤i ≤k,σi的定义类似前面。称S 的子集构成的可数序列{An:n ∈ω}为关于i 的邻域链,如果{An:n ∈ω}满足下面条件:第一,{An:n ∈ω}是非降序列;第二,对于任意n ∈ω 均有An∈(s)成立,其中是µn中关于i 的邻域函数。根据我们对µn的定义,必然存在关于i 的邻域链。定义σi(s)如下:
类似引理2 容易证明µ 是可数融贯网络且容易定义出相应的辅助函数λ。
现在验证µ 是饱和网络。如果D=Dk是µ 中某个缺陷,则存在µn使得Dk在其中是缺陷。注意到D 最坏也是µn+k的最优先缺陷。故并非µn+k+1中缺陷。注意到任取均有对应的(s)是其子集,故U 中存在的证据,矛盾。
推论2(紧致性).对于任意公式集Θ,Θ 是可满足的当且仅当每个有穷子集都是可满足的。
3 群体STIT 理论的能力片段
本节讨论STIT 理论中包含群体的能力片段。我们首先介绍群体STIT 算子的语义推广,并给出当只考虑群体能力片段时,经典BT+AC 模型与邻域STIT 模型的等价性。在后者的基础上,本节证明群体STIT 理论的能力片段具备有穷模型性质。
3.1 语言与语义
预设可数命题变元集PROP、有穷的非空主体集AGT 以及对应的非空群体集GRP,并考虑语义最为简单的CSTIT 算子与历史可能算子。下面给出公式的定义。
定义13(公式).公式由以下BNF 递归定义得到:
将上面定义构造的公式称为群体STIT 逻辑的能力片段,本节中公式均为群体STIT 理论的能力片段公式。
现在说明群体STIT 理论将个体STIT 算子推广为群体STIT 算子这一处理的背后直观:个体i 在状态w 的行动令世界的演变可能局限于Hw,i,个体j 在状态w 的行动令世界的演变可能局限于Hw,j。因此,个体i 与个体j 的联合行动令世界的演变可能局限于,主体的相互独立性确保了并非空集。遵循个体STIT 理论对能动性的刻画,交集便是群体{i,j}能够选择的行动。
定义14(满足).给定经典STIT 模型M 与索引(w,h),邻域STIT 模型M′与状态w′,分别定义◇[G:cstit]φ 在不同模型上的解释:
命题4.公式在经典STIT 模型上可满足当且仅当其在邻域STIT 模型上可满足。
下面现在给出群体STIT 理论的能力片段中公式在有穷模型上满足的充分条件。给定邻域STIT 模型M 与其中状态s 并定义为公式集,用表示前者关于逻辑等值的商集并用表示公式关于逻辑等值的等价类。称模型M 是关于语言证据独立的,当且仅当对于任意i ∈AGT 均存在单射非满射函数满足:如果是公式的证据。
定义15(模态度).函数deg 递归定义如下:
命题5.如果公式在证据独立的模型上是可满足的,则公式在有穷模型上是可满足的。
证明.给定公式φ 并假设存在证据独立的邻域STIT 模型M,w|=φ 成立。将φ中出现的命题变元构成的集合记作P 并假设φ 的模态度为n。如果n=0,命题公式φ 显然能在有穷模型上满足,只考虑n >0 的情况。在逻辑等值的意义下,模态度不大于n 且只由P 中命题变元构成的公式仅有穷多个。给定公式ψ,如果ψ 的模态度不大于n,其中出现的命题变元均出现在P 中且M,w|=ψ,将其记作P(ψ)。
下面证明对于模态度不大于n 且只由P 中命题变元构成的公式ψ 与任意v ∈W′,M,v|=ψ 成立当且仅当M′,v|=ψ 成立。
因此,如果w ∈W′成立,便能直接得到成立。否则,可以扩充W′为W′∪{w},对于任意i ∈AGT,将对应的Ri等价类Xi扩充为。将对应模型记作M′′。类似地,可证明对模态度不大于n 且只由P 中命题变元构成的公式ψ 与任意成立当且仅当成立。
因此,只要证明群体STIT 理论的能力片段中每个公式都是在证据独立的模型上可满足,就证明了群体STIT 理论的能力片段具备有穷模型性质。下面给出群体STIT 理论能力片段的一个公理系统。
定义16(公理系统).表3 与表4 中公理模式5A7 要求G∩G′ 为空集。与推理规则构成希尔伯特式公理系统ABI.C。
命题6(可靠性).公理系统ABI.C 是可靠的。

表3:ABI.C 的公理模式
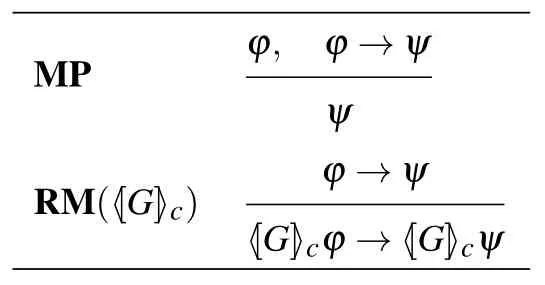
表4:ABI.C 的推理规则
在本节的最后,我们给出一个含历史必然算子□、表示下一刻的明日算子X 以及表示上一刻的昨日算子Y 的群体能力片段的公理系统,可以证明该系统关于文献[12]中离散的关系STIT 框架可靠完全,思路类似于下节证明但需作修改,本文略去这一证明。
定义17(公理系统).表5 与表6 中公理模式与推理规则构成希尔伯特式公理系统ABI.CXY。
命题7(可靠性).公理系统ABI.CXY 是可靠的。
3.2 完全性结果
下面证明上节给出的公理系统ABI.C 的完全性,具体思路依然是为一致公式集逐步构造满足的邻域STIT 模型。我们继续预设AGT={0,...,k}并令GRP 为所有非空群体集。我们直接将简记为。令Φ 为公式集,我们用表示公式集,用表示公式集。
定义18(融贯性).网络µ=(S,{σi:0 ≤i ≤k},ρ)是融贯的当且仅当:

表5:ABI.CXY 的公理模式

表6:ABI.CXY 的推理规则
定义19(饱和性).网络是饱和的当且仅当对于任意公式φ,如果存在s ∈S 与G ∈GRP 满足,则对于任意i ∈G 以及Ui∈σi(s)均存在满足φ ∈ρ(u)。
关于完美网络、由网络生成的模型仿照前面定义,不难验证关于完美网络生成模型的真值引理。
定义20(缺陷).令并令s ∈S,公式为µ中缺陷当且仅当对于任意i ∈G 均存在Ui∈σi(s)满足任意均有。
定义21(辅助函数族).是基于与Γ 的辅助函数族当且仅当:
1.µ 满足融贯条件C1-C4;
2.存在s ∈S 满足Γ ⊆ρ(s)且任意φ ∈Γ 均为形如〈[G]〉cψ 的能力公式;
3.对于任意i 符合0 ≤i ≤k,λi:Γ-→℘(℘(S))是部分函数满足:
按照第2.2 节中的方法并进行适度调整,对于任意极大一致集Σ,我们都可以构造一个可数网络满足:µ 满足融贯条件C1-C4且存在s ∈S 有Σ=ρ(s);存在基于µ 以及的辅助函数族;对于任意i 符合0 ≤i ≤k 与公式φ,并非µ 中缺陷。称满足上述条件的网络µ 是相对于Σ 的个体拟完美网络。
引理4.给定极大一致集Σ,令µ 为相对于Σ 的个体拟完美网络且i ≤k} 为对应的辅助函数族。存在µ 的可数融贯扩充µ*以及基于µ*与的辅助函数族。特别地,µ*是相对于Σ 的个体拟完美网络且是相对于合适的。
最后,对于任意i ∈G,我们要保证新引入的邻域Ui满足融贯条件C3。尽管Ui尚未被定义,我们在下文对它们的指称将不会引起歧义。将记作W,不难发现任意W 对应于一个邻域组合。特别地,对于i ∈G,需要留意i 分量恰好为Ui的向量。将这样的向量构成的W 的子集记作V。
其中,
对于任意i 符合0 ≤i ≤k,称Sj+1的子集构成的可数序列{An:n ∈ω}是关于i的邻域链,如果该序列满足:第一,{An:n ∈ω}是非降序列;第二,存在m ∈ω满足任意n ∈ω 均有;第三,如果An⊂An+1则An+1An与Sjn+m相交为空。定义为:
类似于引理2,容易验证µj+1是满足条件的网络并由此得到相应的辅助函数族。只需要重复上述步骤有穷多次,我们便能得到满足条件的µ*以及相应辅助函数族。
引理5(修补引理).令为可数融贯网络且{λi:0 ≤i ≤k} 为基于µ 以及的辅助函数族,其中s ∈S 成立。假设D 为µ 中缺陷。存在µ 的一个可数融贯扩充以及基于µ′与的辅助函数族满足λ′相对于{λi:0 ≤i ≤k}合适。特别地,D 并非µ′中缺陷。
其中,
容易验证µ′是µ 的可数融贯扩充并定义出相应的辅助函数族特别地,并非µ′中缺陷。
命题8(完全性).一致公式集都是可满足的。
证明.给定一致公式集Σ,将其扩充为极大一致集Σ*,可以得到一个相对于Σ*个体拟完美网络µ,再借助引理4 得到可数融贯网络µ*以及相应辅助函数族利用引理5 并参照命题3 的证明,我们最终得到一个完美网络且Σ 在生成模型中可满足。
推论3(紧致性).对于任意公式集是可满足的当且仅当每个有穷子集都是可满足的。
注意到完全性的证明过程中事实上为每个公式构造了一个证据独立的模型,因此一致公式均能在证据独立的模型上满足,从而可以在有穷模型上满足。
推论4(有穷模型性).群体STIT 理论的能力片段具备有穷模型性质。
4 结语
本文分别讨论了个体STIT 理论与群体STIT 理论的能力片段,给出了与经典STIT 模型等价的邻域STIT 模型。我们为这两个片段分别提供了希尔伯特式公理系统,并利用邻域STIT 模型与逐步构造法得到了公理系统的完全性。利用群体STIT 理论能力片段的完全性结果,我们证明了该片段具备有穷模型性质。
本文利用个体STIT 理论的既有结果得到了个体STIT 理论能力片段的可判定性与复杂度上限,但个体STIT 理论能力片段的算法复杂度却依然未明。另一方面,利用群体STIT 理论能力片段的有穷模型性质将有望得到群体STIT理论能力片段的可判定性,这有待我们后面的研究。
本文在讨论STIT 理论能力片段的时态扩充时只简单提到了与明日算子X和昨日算子Y 的结合,对能力片段进行时态扩充将是我们的另一目标。通过在语言中增添表示将来的将来算子F 与过去的过去算子P,我们甚至能讨论个体与群体在过去、当前与将来的能力。具体的讨论也是我们今后的工作方向。
