往复压缩机管路大气流脉动的数值模拟和实验研究

李元,全恺,吴睿,畅云峰,郭蓓,张博

(1.西安交通大学能源与动力工程学院,710049,西安;2.中石化川气东送天然气管道有限公司,430020,武汉)

往复活塞式压缩机中,由于靠气阀控制气体进出气缸,进排气管路中的气流时断时通,从而产生较大的气流脉动[1]。气流脉动对往复压缩机产生诸多影响,会引起管道振动、降低压缩机性能,改变气阀工况,使得控制仪表失灵等,影响压缩机的经济性及生产安全性[2]。因此,对于控制气流脉动,准确预测气流脉动十分重要[3]。

目前,压缩机中压力脉动的分析计算主要基于平面波动理论和一维非定常理论[4]。对一般的压缩机装置,通过平面波动理论进行求解方便可行[5-8]。专门的计算应用软件Pulse可解决大量工程应用中的气流脉动问题[9-10]。另外,有学者使用商用模拟软件,对气流脉动进行三维模拟[11-14],但该方法计算量大,计算过程复杂。对于压缩机管路,由于长度方向的尺寸远大于其他维度尺寸,简化为一维模型在工程应用上是可行的,三维模拟更适用于形状复杂的腔室结构。平面波动理论是基于小振幅(压力不均匀度小于8%)气流脉动的假设进行计算的[3,15],某些微小型活塞压缩机的转速较高且空间狭小,管路中的气流脉动相对较大,如果继续采用平面波动理论计算气流脉动,则会带来较大误差。

本文研究大脉动工况下管路的气流脉动,应用一维非定常可压缩流动理论进行求解。传统的压缩机管路气流脉动模拟直接从管路的入口着手分析,没有考虑到吸排气阀腔容积的影响,为了使模拟结果更为准确,本文在建立模型时将阀腔容积及排气阀通道看作是管路系统的一部分,搭建了往复压缩机管路气流脉动测量实验台。

1 数学模型

1.1 一维非定常流动的基本方程组

压缩机进排气管路中,管道的直径尺寸远小于管路的长度尺寸,可认为在某一横截面上的各个参数都相等,因此把管路内的流动简化为一维流动。在管路内取细微的流体单元作为研究对象,根据质量守恒、能量守恒和动量守恒定律,得到一维非定常流动理论的控制方程组

(1)

式中:p=p(x,t)、ρ=ρ(x,t)、u=u(x,t)分别为管道内某一截面气体的压力、密度和速度,均与x和t有关,x为距离端点的长度,t为气体流动的时间;Φ=-4gf|u|u/(2D)为流体所受的摩擦力,其中f为摩擦系数,D为管道直径,g为重力加速度;k为比热容比;q为单位时间内单位质量气体与外界的热交换,输入控制体的热量取正值,输出热量取负值。

将各个参数量纲一化并引入以下符号

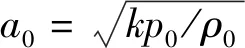
(2)

式中:Z=a0t/L0为量纲一时间;X=x/L0为量纲一距离。

一维非定常气流方程组的求解使用两步法和匀熵修正理论特征线法相结合的方法,即管道内部的点使用两步法计算,边界点使用特征线法计算。

1.2 方程组求解

1.2.1 两步Lax-Wendroff有限差分格式 在求解一维非定常流动方程组时,两步Lax-Wendroff格式很好地平衡了计算效率、计算精度和稳定性三者之间的关系,被认为是最适合求解的差分格式。两步法的基本原理是:利用某一个点Z时刻的速度、压力和密度和其相邻两个点Z时刻的气流参数值推算出该点在Z+ΔZ时刻的气流参数值,计算过程示意图如图1所示。

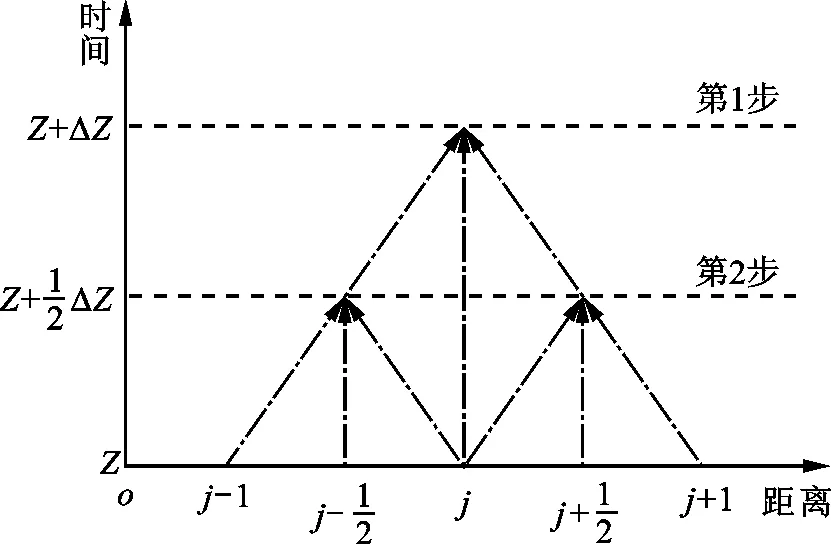
图1 两步法计算过程示意图

求解式(2)的两步法中第1、2步表达式为

(3)

(4)

因为缺少一个相邻点的信息,边界点无法用两步法进行计算,所以要借助特征线法进行求解。

1.2.2 匀熵修正理论特征线法的插值公式 匀熵修正理论只考虑管路中的摩擦,忽略管道与环境的换热,认为管道内的气体流动是等熵过程,从而对端点的参数进行求解。引入两个黎曼变量

(5)

式中A=at/a0为量纲一声速。

匀熵修正理论给出的气流无量纲特征型方程组可表示为

(6)

求解时,取满足稳定性的时间步长ΔZ与距离步长ΔX组成计算网格,用插值方法可得第一特征线的黎曼变量

(7)

同理,第二特征线插值公式为

(8)

在端点处,已知本时刻参数值以及与端点相邻一点的参数值,可得下一时刻的黎曼变量。根据黎曼变量以及已知的边界条件,可得端点处下一时刻的压力及速度。

1.3 管路边界点处理

1.3.1 端点为压缩机短管容器的情况 考虑阀腔的影响,压缩机气阀通道处的边界条件可简化为压缩机-短管-容器(简称为压-管-容)的情况,示意图如图2所示,1点连接压缩机端,1-2为短管,2-3为容器,在这个模型中已知Z时刻3点的参数值和1点处的速度可计算出这3点下一时刻的气体参数。

2-3容器单元可看作一种横截面足够大、而管长与截面相比足够小的特殊管,假定性质参数只与时间有关,与在容器内的位置无关。根据气流的连续条件可得连续方程

(9)

式中:S2、S3为容器进出口的通流面积;v为容器的容积。

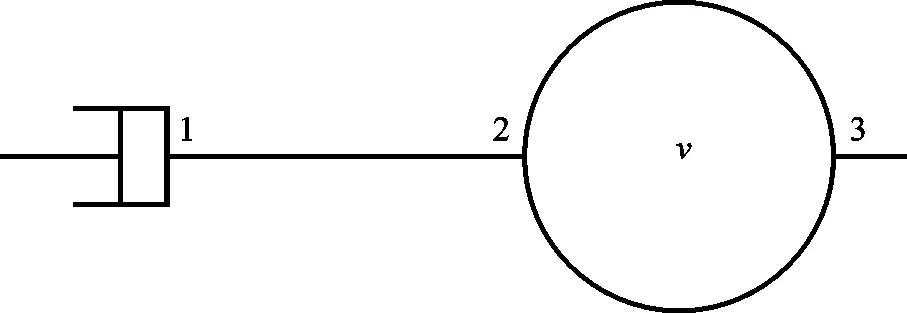
图2 压-管-容示意图

用差分方法即可求得Z+ΔZ时刻容器内压力P′的表达式

(10)

进而求得其他参数

(11)

(12)

(13)

式中:Ld为短管长度;Dd为短管内径;U′为Z+ΔZ时刻管路的激发速度。

1.3.2 异径管单元 对于变截面排气管路可采用异径管单元进行计算,异径管示意图如图3所示。

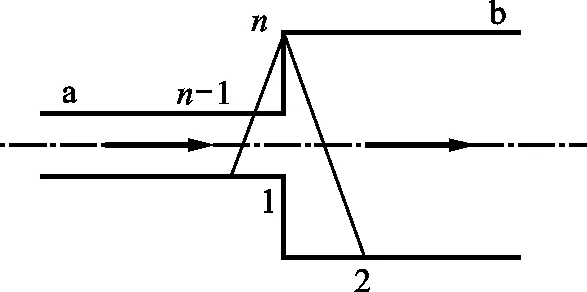
图3 异径管示意图

(14)

式中:Sn、S1分别为a管、b管的通流面积。

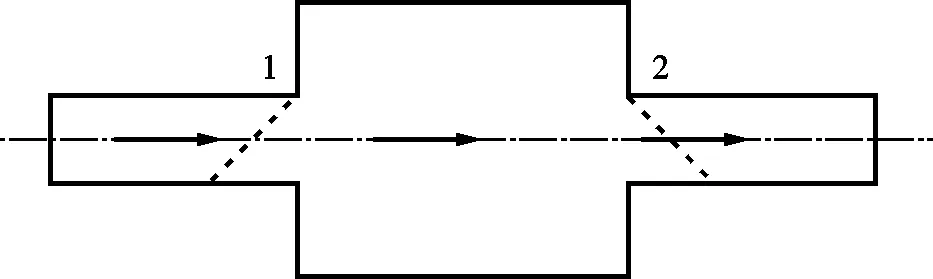
图4 容积腔示意图

2 实验验证

为验证一维非定常流动理论的数值模型及其解法在实际压缩机管路上的适用性,探究一维非定常方法模拟程序对不同转速和不同边界条件模拟的准确性,本文搭建了管路大气流脉动实验台,测试了变转速条件下不同管路单元系统的气流压力脉动。

2.1 测试系统介绍

实验台采用的压缩机是一台V型单级单作用往复式空气压缩机,具体参数如表1所示。压缩机的电机与一台变频器相连,通过改变变频器输出来改变电机的运转频率,从而改变压缩机的转速。管路末端与储气罐相连,储气罐的出口处设有阀门,通过调节阀门的开度,可改变管道内压力,实验测试了3种管系的脉动压力。

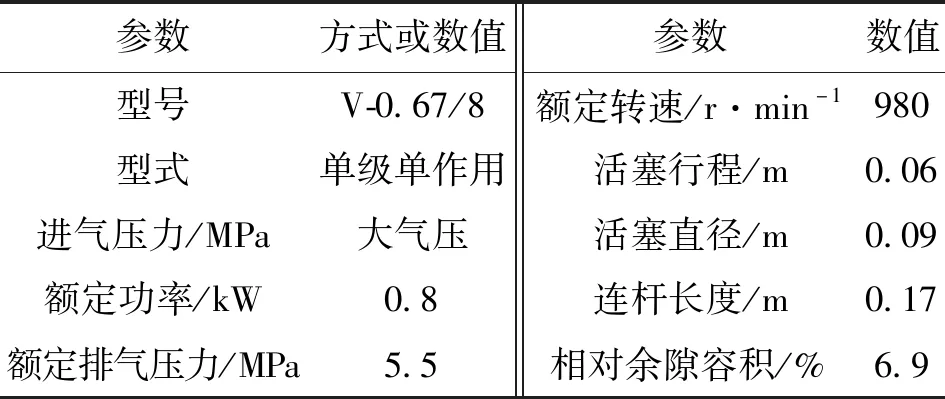
表1 实验用压缩机主要规格参数

2.2 实验测点分布

每种管系分别布置3个测点,3个管路系统的测点布置位置及压力传感器安装位置如图5所示,具体位置为:测点1均在压缩机排气出口处,单直管管系的测点2在管路中点处,测点3在距压缩机排气口1.5 m处;容积腔管系的测点2在容积腔进口处,测点3在容积腔出口处;异径管管系的测点2在异径粗管进口处,测点3在异径粗管出口处。

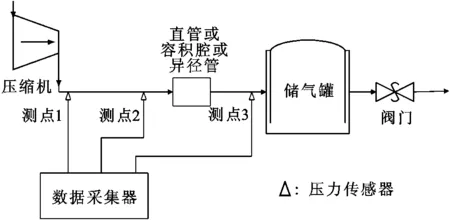
(a)测量系统

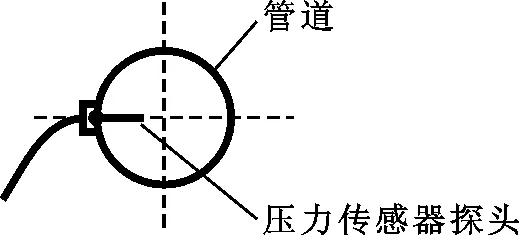
(b)压力传感器安装位置图5 测量系统及压力传感器安装位置

2.3 动态压力测试系统

压缩机管路内的动态压力测量系统由两部分组成,分别为压力传感器和信号采集处理系统。实验选择XTL-190(M)系列小型压力传感器,选用的传感器量程为0～0.7 MPa,固有频率为380 kHz。转速采用数字式高精度光电式转速测量仪进行测量,测量范围为2.5～99 999 r/min,转速在2.5～999.9 r/min时,分辨率为0.1 r/min,转速大于1 000 r/min时,分辨率为1 r/min。实验采用NI-PXIe1078采集仪,采集仪搭载了PXIe-6356电压信号采集板卡,模拟带宽为1 MHz。

3 结果分析

本文采用压力不均匀度来体现压力脉动的大小,表达式为

(15)

3.1 一维非定常和平面波动理论计算结果比较

在排气压力为0.5 MPa、转速为496 r/min时,单直管管系测点1的一维非定常和平面波动理论计算与实验结果的对比如图6所示。由图6可知:压力不均匀度分别为19.84%、26.41%、17.51%,属于大气流脉动;平面波动理论计算的压力幅值大于实验结果和非定常方法的计算结果,同时相位角上也相差较大。这说明在处理脉动较大的情形时,平面波动理论不能准确反映出实际管路内的气流脉动,而非定常方法计算结果可很好地预测管路内的气流压力脉动。

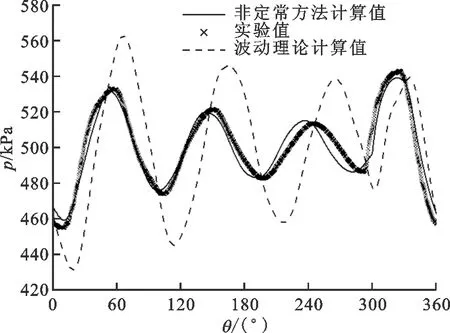
图6 一维非定常和平面波动理论计算与实验结果的对比

3.2 阀腔模型的简化及其对模拟结果的影响

图7 加阀腔、不加阀腔的计算值与实测值对比

为了使模拟结果更为准确,本文在建立模型时将阀腔容积及排气阀通道看作是管路系统的一部分,并将气阀通道、阀腔和气缸简化成压缩机-短管-容器边界模型。转速为980 r/min、排气压力为0.5 MPa时单直管管系测点1的实验结果,与考虑、不考虑阀腔的模拟结果对比如图7所示。由图7可知:压力不均匀度分别为29.43%、30.53%、29.81%,符合大脉动要求;加阀腔简化模型后模拟得到的波形图与实测结果吻合较好,而不考虑阀腔模拟得到的压力波形图与实测值相差很大,这说明在压缩机管路气流脉动模拟时应当考虑阀腔容积的存在,将其简化为压-管-容边界模型后得到的模拟结果更与实际情况吻合。因此,本文在后续的模拟计算中考虑阀腔的容积,并将阀腔和气阀通道分别简化为容积和短管单元。

3.3 不同转速下的比较

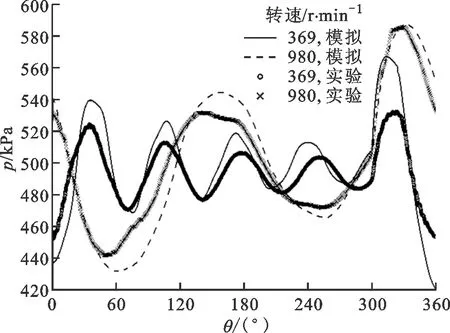
(a)测点1

(b)测点2

(c)测点3图8 不同转速时实验、模拟结果的波形图

对不同管系不同测点在转速为369、980 r/min的管路内气流脉动进行了测量,排气压力为0.5 MPa时单直管管系3个测点的压力波形如图8所示。由图8可知,测点在不同转速时实验、模拟结果的压力不均匀度均大于8%,属于大脉动工况;不同转速下的模拟、实验结果的波形图吻合较好,变化规律一致;转速为369 r/min时,3个测点的模拟、实验结果的最大相对误差分别为6.8%、5.4%和8.3%;转速为980 r/min时,3个测点的模拟、实验结果的最大相对误差分别为2.9%、1.7%和3.3%。误差均在允许范围之内,说明一维非定常流动理论计算的结果在时域下与实验结果相吻合。

对实验管系气柱固有频率进行了计算,得到该实验管系的一阶气柱固有频率为33.5 Hz。测点1在369、980 r/min转速下的傅里叶分解幅值频谱如图9所示。由图9可知,模拟、实验结果的变化趋势一致,幅值均在接近固有频率时达到最大值,验证了一维非定常流动理论计算的结果不仅在时域下与实验结果相吻合,在频域下与实验结果相对应。

(a)转速为369 r/min

(b)转速为980 r/min图9 不同转速时傅里叶分解幅值频谱图

3.4 不同管系下的比较

变转速分析均基于单直管管系,说明了一维非定常模拟程序在计算单直管管系压力脉动时的准确性。下文将通过分析另外两种管路系统时实验、计算结果之间的差异,来验证一维非定常模拟程序中对不同管系模拟的准确性。

排气压力为0.4 MPa时,两种管系不同测点在转速为814 r/min的波形图如图10所示,可见压力不均匀度均符合大脉动要求。由图10可知,实验与模拟所得波形图变化规律一致,容积腔管系3个测点模拟、实验结果的最大相对误差分别为7.4%、2.6%和0.5%;异径管管系3个测点模拟、实验结果的最大相对误差分别为9.4%、2.7%和2.4%。误差在允许范围之内,说明该模型在不同管系时的模拟结果能准确反映出实际管路内的压力脉动情况。

(a)容积腔管系

(b)异径管管系图10 容积腔管系和异径管管系的压力波形图

4 结 论

本文针对活塞式压缩机大脉动工况管路气流脉动进行了数值模拟和实验研究,基于一维非定常流动理论建立了不同管系条件下的数学模型。传统的压缩机管路气流脉动模拟没有考虑到吸排气阀腔容积的影响,而实际上阀腔对气流脉动会产生相位上的延迟作用,当阀腔较大时,还会起到缓冲容积的作用,对压力脉动幅值产生影响。因此,为了使模拟结果更为准确,本文在建立模型时将阀腔容积及排气阀通道都看作是管路系统的一部分。同时,搭建了管路大气流脉动验证实验台,测试了大脉动工况下单直管管系、容积腔管系和异径管管系在不同转速下的气流脉动情况,结论如下。

(1)在大脉动工况下,采用平面波动理论计算所得波形图与实测波形图相位和幅值均差别较大,而采用一维非定常理论所得波形图与实测波形图变化规律一致,吻合度较高。

(2)对比了大脉动工况下加阀腔模型和不加阀腔模型模拟结果与实测值之间的差别,结果表明加阀腔模型能得到更为准确的模拟结果。在大脉动工况下,须考虑排气阀通道及排气阀腔的影响,并可将它们分别简化为短管和容积单元。

(3)不同转速、不同管系条件下的模拟结果和实验测得的波形变化规律一致,波形吻合较好,且计算所得波形图与实测波形图的最大误差在10%以内,证明本文基于一维非定常流动理论所建数学模型和模拟程序准确。