钢−混凝土组合梁高强螺栓抗剪连接件受剪性能

陈俊，汪威，丁发兴，许福，龙士国，杨才千, 3

钢−混凝土组合梁高强螺栓抗剪连接件受剪性能

陈俊1，汪威1，丁发兴2, 4，许福1，龙士国1，杨才千1, 3

(1. 湘潭大学 土木工程与力学学院，湖南 湘潭 411105；2. 中南大学 土木工程学院，湖南 长沙 410075；3. 东南大学 土木工程学院，江苏 南京 210018；4. 湖南省装配式建筑工程技术研究中心，湖南 长沙 410075)

采用ABAQUS有限元软件对钢-混凝土组合梁高强螺栓抗剪连接件的受剪性能进行三维实体有限元非线性分析，模型考虑钢梁、混凝土板和高强螺栓等材料非线性以及各部件之间的接触关系，在试验验证的基础上探讨混凝土强度以及高强螺栓直径、屈服强度、长径比和预紧力等参数对抗剪承载力的影响，分析结果表明：高强螺栓连接件的抗剪承载力随混凝土强度、螺栓直径与屈服强度的增大而提高。通过拟合建立考虑混凝土强度、高强螺栓直径和屈服强度影响的单个连接件抗剪承载力计算式，并对现行规范中栓钉受剪计算公式和国外学者及本文提出的高强螺栓受剪计算公式的计算值进行比较，结果表明本文提出的计算式具有较高的精度。

钢-混凝土组合梁；高强螺栓抗剪连接件；推出试验；有限元；受剪性能

抗剪连接件是确保组合梁中钢梁与混凝土板共同工作的关键元件。栓钉连接件具有各向同性、受力性能好、制造工艺简单等优点被广泛应用于组合结构及桥梁工程中，国内外对其抗剪性能的研究也取得了一定的成果[1−5]。目前，国家正大力发展装配式建筑，高强螺栓可作为一种可装配拆卸栓钉替代传统栓钉应用到钢−混凝土组合梁中以提高装配效率。已有国内外学者对钢−混凝土组合梁高强螺栓抗剪连接件进行相关试验研究[6−9]，结果表明：高强螺栓的抗剪承载力明显大于栓钉，欧洲Eurocode 4规范[10]建议的栓钉抗剪承载力计算公式预测高强螺栓抗剪承载力将偏于保守。在组合梁抗剪连接件数值模拟方面，国内外研究较多的是栓钉剪力连接件[11−15]，研究成果表明混凝土强度等级、栓钉直径和屈服强度对连接件的抗剪承载力都有影响，但有关高强螺栓抗剪连接件的数值研究依旧较少，且关于其受剪承载力计算方法的研究也比较少见。LIU等[16]采用ABAQUS有限元软件对高强螺栓抗剪连接件预留孔推出试验进行数值模拟，混凝土采用新型材料(GPC)，模型中高强螺栓采用理想弹塑性本构，并对Kwon等[9]建议的连接件抗剪承载力计算公式进行改进，但改进后的公式没有考虑混凝土强度的影响。Hassanieh等[17]采用ABAQUS软件对高强螺栓连接件预留槽口木−钢梁推出试验进行有限元分析，并分别对单个参数影响下的受剪承载力提出计算式。钢−混凝土组合梁高强螺栓连接件受力复杂，且影响因素较多，各因素对其受剪承载力的影响也并非单独作用。为研究钢−混凝土组合梁高强螺栓抗剪连接件的受剪性能，作者在对钢−混凝土组合梁栓钉抗剪连接件受压、受拉静力及往复推出研究成果[11, 15, 18]的基础上，主要工作如下：1) 采用ABAQUS有限元软件，对国内外相关学者进行高强螺栓连接件推出试验结果进行非线性仿真分析与验证；2) 根据有限元模型对混凝土的强度等级和高强螺栓的直径、长径比、屈服强度及预紧力等参数对受剪承载力的影响进行分析，提出高强螺栓连接件抗剪承载力计算公式；3) 根据有限元算例计算值结合已有文献试验值，对现行规范中建议的、国外学者及笔者提出的高强螺连接件抗剪承载力计算公式的计算值进行比较。

1 有限元模型及验证

1.1 计算模型

文献[6−8]推出试验的设计简图如图1所示，其中文献[6]每侧混凝土板含4个抗剪连接件，文献[7−8]每侧只含2个连接件。

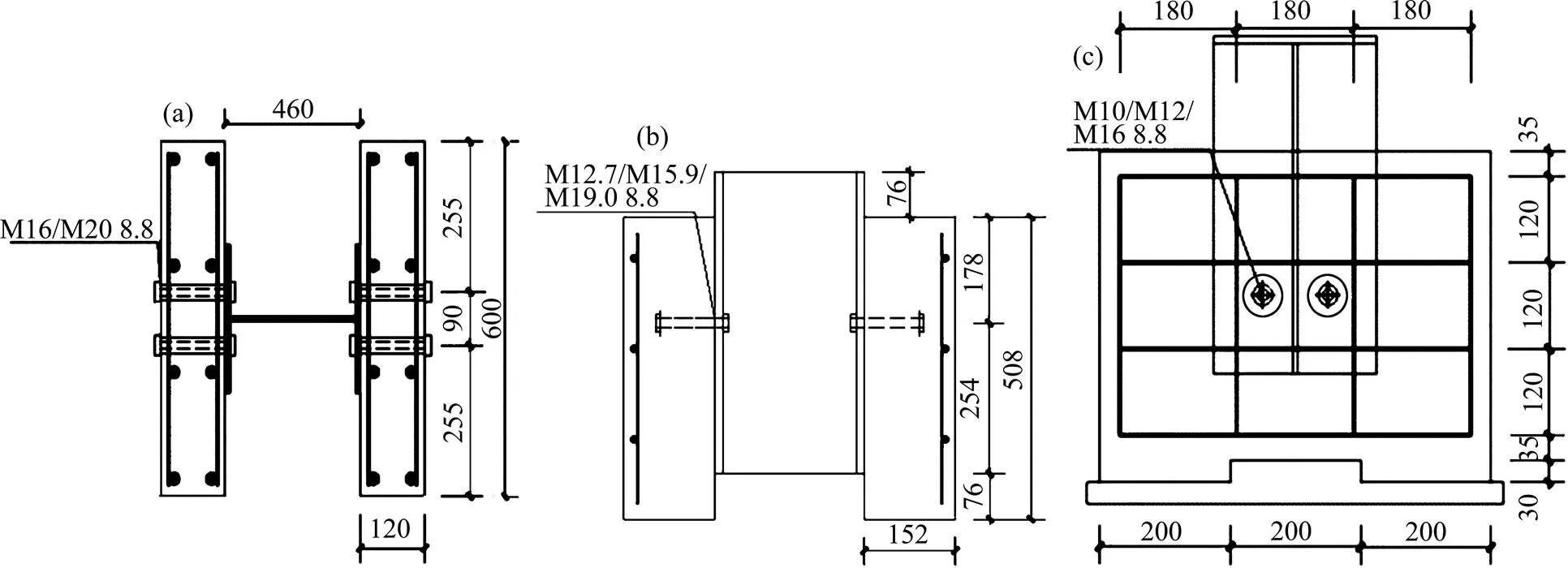
(a) 平面图；(b) 立面图；(c) 侧面图

1.2 模型建立

1.2.1 材料本构关系

采用ABAQUS/Standard6.12[19]有限元软件进行建模分析，混凝土、钢梁和钢筋的本构模型见文 献[20]，高强螺栓本构采用三折线材料模型[21]：

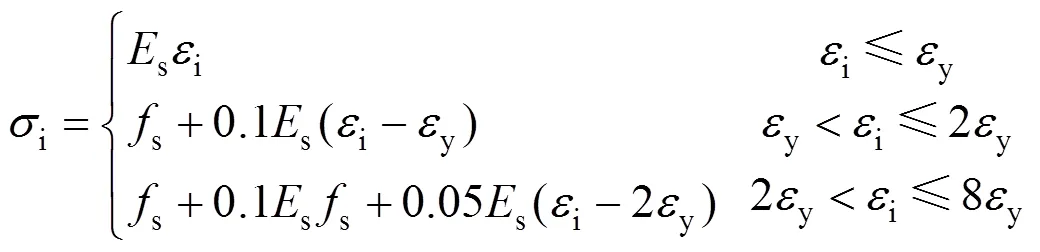
式中：i为高强螺栓的等效应力；i为高强螺栓的等效应变；y为屈服时的应变；s为高强螺栓的弹性模量；s为屈服强度。由于试验从开始加载到破坏，螺帽与螺杆两者之间的滑移量很微小，可以把螺帽和螺杆作为整体共同建模。对文献[6−8]中没有给出高强螺栓具体材性试验数值的，取高强螺栓名义屈服强度和抗拉强度进行计算。

1.2.2 单元类型与网格划分

混凝土、钢梁和高强螺栓都采用八节点三维实体线性减缩积分单元(C3D8R)，沙漏(hourglassing)控制。钢筋采用三维桁架线性单元(T3D2)。考虑到推出试验的对称性，本文采用试验模型的1/4结构进行建模分析，该有限元模型包含混凝土板、高强螺栓、钢梁、纵筋和箍筋4个部分。高强螺栓的螺纹部分按等效换算的净截面直径建模，螺栓大六角头也进行等直径换算；混凝土板的孔洞和钢梁的孔洞由布尔操作完成。网格划分均采用结构化网格划分技术，对混凝土孔洞和钢梁孔洞附近应力集中区域采用相对较细的网格划分，对其余部分采用较粗的网格划分。高强螺栓抗剪连接件三维实体精细有限元模型的网格划分如图2所示。

1.2.3 界面的模拟

钢梁与混凝土板的接触采用面−面(Surface- to-Surface)接触，设置法线方向的硬接触(hard)和切线方向的摩擦接触，其中摩擦因数按文献[6−8]中给定数值取值，对于文献中没有给出具体摩擦因数的，则取值参考JGJ82—2011钢结构高强螺栓连接技术规程[22]。

高强螺栓与混凝土板的接触分为径向和环向2个接触方向。径向：混凝土板与螺帽的径向、螺栓大六角头的径向接触都设为法线方向的硬接触，并设置允许接触后分离；环向：混凝土板与螺帽的环向、大六角头的环向接触，设为法线方向的硬接触和切线方向的摩擦接触。

(a) 混凝土单元；(b) 钢梁单元；(c) 高强螺栓单元；(d) 钢筋单元

图3 螺栓荷载的施加

钢梁与螺杆的接触设为法线方向的硬接触，并设置允许接触后分离；螺帽与钢梁的接触设为法线方向的硬接触和切线方向的摩擦接触。钢筋采用Embedded方式嵌入混凝土板中，不考虑两者之间的黏结滑移效应，使两者有相同的平动自由度。

1.2.4 边界条件

对图2 1/4模型施加对称边界条件。分别对面1施加轴方向(U=UR=UR=0)，面2施加轴方向(U=UR=UR=0)对称边界条件，对面3施加固定边界条件。

1.2.5 施加荷载与定义分析步

钢梁顶面作为加载面并采用位移控制加载，有限元模型计算分析步共分为5步：1) 接触关系、边界条件在初始分析步中建立，并传递到后续的分析步中；2) 施加螺栓预紧力，采用螺栓荷载(Bolt Load)方式进行施加，为了让螺栓与钢梁、螺栓与混凝土板之间的接触缓慢平稳地建立，先施加微小的荷载；3) 施加高强螺栓试验时实际大小的预紧力，或取值参考GB50017—2017钢结构设计规范[22]建议值。4) 固定螺栓的长度；5) 对钢梁顶面施加位移荷载。文献[8]计算模型中螺栓荷载的施加如图3 所示。

1.3 模型验证及分析

有限元模型计算得到的荷载−滑移曲线与试验荷载−滑移关系曲线的比较如图4所示，可以看出：1) 对于文献[7−8]试验曲线，由于螺栓与混凝土之间充分接触无间隙，混凝土对螺栓的约束作用较强，荷载−滑移曲线与传统栓钉连接件类似。图4(c)和4(d)中NB，RPB和CPB分别表示高强螺栓连接件现浇、普通预留孔和预埋波纹管灌浆推出试件，其中刘中良[8]有限元计算曲线是各种对比试验曲线的上限且与CPB推出试件最为接近。由于高强螺栓未进行螺纹建模，因此在弹塑性阶段有限元计算曲线刚度较实际推出试件大，但两者峰值荷载相差不大。总体而言，有限元模型可以反映实际推出试件的抗剪承载力；2) Ataei等[6]由于混凝土板预留孔洞、钢梁孔洞与螺栓之间存在不同大小的间隙，因此有限元荷载−滑移曲线在螺栓预紧力被克服之后出现明显的滑移平台。图4中b表示螺栓预紧力值，考虑推出试件高强螺栓在施加预紧力或装配搬运过程中，螺栓与混凝土板预留孔洞、钢梁孔洞之间存在错动，并非如有限元模型那样完全对中，因此试验中的滑移平台相对不明显。总体来说，有限元模型可以反映实际推出试件的抗剪承载力。图5所示为文献[6, 8]有限元计算模型所得高强螺栓von- Mises应力与变形云图与试验破坏形态的对比，可见试验破坏形态与有限元破坏都是高强螺栓被 剪断。

(a) 文献[6]16，20mm连接件；(b) 文献[7]15.9mm，19mm连接件；(c) 文献[8]10，16 mm连接件；(d) 文献[8]12mm连接件

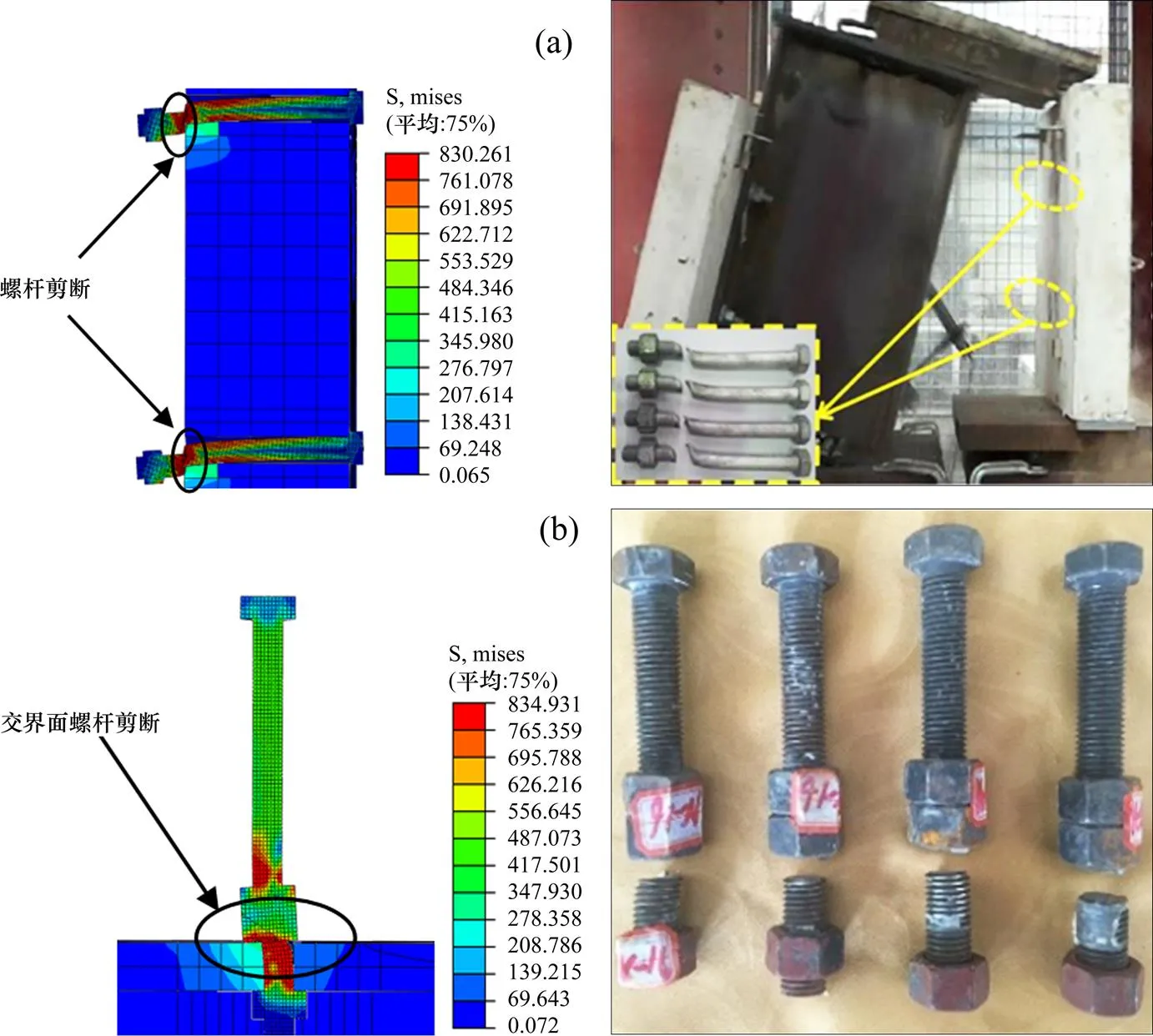
(a) 文献[6]20 mm高强螺栓；(b) 文献[8]16mm高强螺栓

2 抗剪承载力分析与比较

2.1 参数分析

由于高强螺栓连接件推出试验荷载−滑移曲线没有明显的下降段，因此，本文将抗剪承载力定义为连接件的峰值荷载，采用ABAQUS有限元软件对单个高强螺栓连接件抗剪承载力的参数分析如下：

1)混凝土强度。以螺杆长度=150mm，嵌入长度E=100mm，屈服强度s=640MPa，直径为10~20mm的高强螺栓抗剪连接件为例，图6(a)所示为不同混凝土强度对抗剪承载力的影响，可知当高强螺栓直径和屈服强度相同时，提高混凝土的强度可以提高螺栓的受剪承载能力。当混凝土强度从C20增大到C60时，10~20mm高强螺栓的极限承载力分别提高22%，32%，31%，35%和34%。

2) 高强螺栓直径。以螺杆长度=150mm，嵌入长度E=100mm，屈服强度s=640MPa，混凝土强度为C20~C60的高强螺栓抗剪连接件为例，图6(b)所示为不同高强螺栓直径对抗剪承载能力的影响，可见混凝土强度相同时，高强螺栓连接件的抗剪承载力随着直径的增大而明显增大。当混凝土强度为C40时，直径从10~16mm时，此时平均直径每增加2mm，抗剪承载力平均增幅达35%；当直径16~20mm时，直径每增加2mm，抗剪承载力平均增幅为20%。

3)高强螺栓屈服强度。以螺杆长度=150mm，嵌入长度E=100mm，混凝土立方体抗压强度为40MPa高强螺栓抗剪连接件为例，图6(c)所示分析为不同屈服强度对抗剪承载能力的影响，可知高强螺栓的抗剪承载能力随着屈服强度的提高而几乎线性增加。

4) 高强螺栓长径比。以混凝土立方体抗压强度为40MPa，屈服强度s=640MPa，直径分别为10，12和16mm的高强螺栓抗剪连接件为例，图6(d)所示为不同直径长径比对高强螺栓抗剪承载能力的影响。由图可知，当长径比较小时，连接件抗剪承载力随高强螺栓长径比的增大而提高，但当长径比大于4时，抗剪承载力增幅较小。文献[13]有限元分析结论有着类似规律。

5) 高强螺栓预紧力。以混凝土立方体抗压强度为40MPa，屈服强度s=640MPa，嵌入长度E=100mm，直径为10~16mm的高强螺栓抗剪连接件为例，图6(e)所示为不同预紧力对高强螺栓抗剪承载能力的影响，横坐标表示规范[23]中建议施加的预紧力。可见预紧力大小对高强螺栓连接件抗剪承载力的影响较小，文献[17, 24]也有着类似结论。

综上所述，钢−混凝土组合梁高强螺栓抗剪连接件的抗剪承载力随混凝土强度、螺栓的直径以及屈服强度的增大而提高，其中增大高强螺栓直径对提高连接件的受剪承载力最有效。

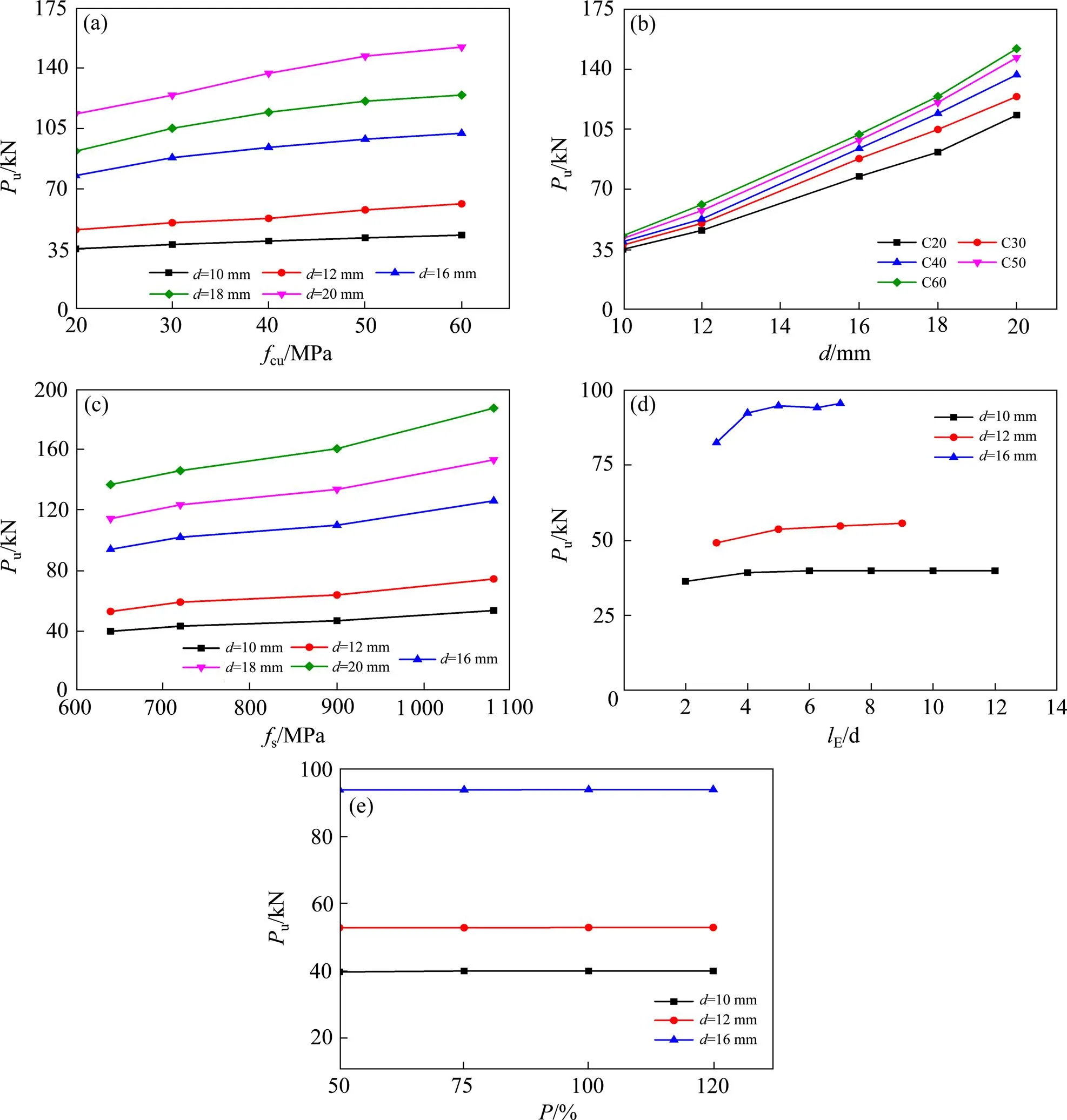
(a) 混凝土强度；(b) 高强螺栓直径；(c) 高强螺栓屈服强度；(d) 高强螺栓长径比；(e) 高强螺栓预紧力

2.2 高强螺栓抗剪承载力计算公式

基于有限元参数分析，考虑混凝土强度cu(C20~C60)，高强螺栓直径(10~20mm)以及屈服强度s(640~1 080MPa)的影响，通过拟合回归，提出单个高强螺栓抗剪承载力计算公式：

图7所示为式(2)计算值与本文有限元算例计算值的比较，图8所示为式(2)计算值与文献[6−9,24−25]试验值之间的比较，其中纵坐标Pu,f和Pu,0分别表示有限元计算值和试验值，横坐标Pu,c表示式(2)计算值，有限元计算值与式(2)计算值之比均值为1.010，均方差为0.025，试验值与式(2)计算值之比均值为0.988，均方差为0.161，可见本文提出的计算式(2)精度较好。

图8 公式计算值与文献[6−8,24−25]试验值之间的比较

2.3 公式比较

目前各国规范对于钢−混凝土组合梁高强螺栓抗剪连接件的计算尚未给出相关计算公式。本文基于文献[6−9, 24−25]中的85组试验值和本文45组有限元算例计算值，通过与中国GB50017—2017[23]规范、美国AISC360−16[26]规范和欧洲Eurocode 4[10]规范中建议的栓钉抗剪承载力公式计算值，以及Kwon等[9]、LIU等[16]和笔者提出的高强螺栓抗剪承载力计算公式的计算值进行比较，各计算公式见表1，比较结果见表2和表3。

表1 各国规范与学者提出的受剪承载力计算公式

表2 45个有限元算例计算值与各公式计算值的比较

注：u,(i)表示文中建议公式(i)计算值；为u,0/u,(i)的平均值；为u,0/u,(i)的离散系数。

从表2和表3中可以看出：1) 笔者提出的计算式，精度最高，适用性更广；2) 各国规范栓钉建议公式计算值及国外学者提出的公式计算值较试验值和算例分析计算值都偏小，其中ANSI/AISC360- 16[26]和LIU等[16]建议的公式计算值相对较接近。

表3 试验值与有限元计算值及各公式计算值的比较

3 结论

1) 建立的钢−混凝土组合梁高强螺栓抗剪连接件三维实体精细有限元模型计算结果与各文献试验结果吻合良好。

2) 有限元参数分析结果表明：高强螺栓连接件抗剪承载力随混凝土强度、螺栓直径及屈服强度的增大而提高，螺栓长径比及预紧力对抗剪承载力影响较小；基于参数分析提出考虑不同混凝土强度、高强螺栓直径及屈服强度的抗剪连接件受剪承载力计算式，公式结果与算例计算结果及试验结果吻合较好。

3) 通过与GB50017—2017《钢结构设计标 准》、ANSI/AISC360-16和Eurocode 4规范中栓钉抗剪承载力建议公式与Kwon和LIU等提出的公式进行比较，结果表明，所建立的计算公式精度较高。

[1] Ollgaard J G, Slutter R G, Fisher J W. Shear strength of stud connectors in lightweight and normal-weight concrete[J]. AISC Engineering Journal, 1971, 8(2): 55− 64.

[2] Shim C S, Lee P G, Yoon T Y. Static behavior of large stud shear connectors[J]. Engineering Structures, 2004, 26(12): 1853−1860.

[3] 聂建国, 沈聚敏, 袁彦声, 等. 钢−混凝土组合梁中剪力连接件实际承载力的研究[J]. 建筑结构学报, 1996, 17(2): 21−28. NIE Jianguo, SHEN Jumin, YUAN Yansheng, et al. Study on the actual bearing capacity of shear connectors in steel-concrete composite beams[J]. Journal of Building Structures, 1996, 17(2): 21−28.

[4] 薛伟辰, 丁敏, 王骅, 等. 单调荷载下栓钉连接件受剪性能试验研究[J]. 建筑结构学报, 2009, 30(1): 95−100. XUE Weichen, DING Min, WANG Hua, et al. Experimental studies on behavior of stud shear connectors under monotonic loads[J]. Journal of Building Structures, 2009, 30(1): 95−100.

[5] 周凌宇, 伏荣. 重复荷载作用下栓钉连接件力学性能的试验研究[J]. 铁道科学与工程学报, 2010, 7(3): 31− 36. ZHOU Lingyu, FU Rong. Experiment study on mechanical behavior of the stud connector under repeated load[J]. Journal of Railway Science and Engineering, 2010, 7(3): 31−36.

[6] Ataei A, Bradford M A, Xinpei L. Sustainable composite beams and joints with deconstructable table bolted shear connectors[C]// Proceedings of the 23rd Australasian Conference on the Mechanics of Structures and Materials, Byron Bay, Australia, 9−12. 2014.

[7] Lawrence N D. High strength bolt shear connectors- pushout tests[J]. Journal Proceedings, 1968, 65(9): 767− 769.

[8] 刘中良. 装配式组合梁高强螺栓连接件抗剪性能试验研究[D]. 湘潭: 湘潭大学, 2017. LIU Zhongliang. Experimental study on the shear behavior of the prefabricated composite beam high strength bolt connector[D]. Xiangtan: Xiangtan University, 2017.

[9] Kwon G, Engelhardt M D, Klingner R E. Behavior of post-installed shear connectors under static and fatigue loading[J]. Journal of Constructional Steel Research, 2010, 66(4): 532−541.

[10] Eurocode 4. Design of composite steel and concrete structures, Part 1.1: General rules and rules for buildings[S]. Brusseles, Belguim, 2004.

[11] DING F X, YIN G A, WANG H B, et al. Static behavior of stud connectors in bi-direction push-off tests[J]. Thin-Walled Structures, 2017, 120: 307−318.

[12] Lam D, Elliott K S, Nethercot D A. Parametric study on composite steel beams with precast concrete hollow core floor slabs[J]. Journal of Constructional Steel Research, 2000, 54(2): 283−304.

[13] Pavlović M, Marković Z, Veljković M, et al. Bolted shear connectors vs. headed studs behaviour in push-out tests[J]. Journal of Constructional Steel Research, 2013, 88: 134−149.

[14] XU C, Sugiura K, WU C, et al. Parametrical static analysis on group studs with typical push-out tests[J]. Journal of Constructional Steel Research, 2012, 72(5): 84−96.

[15] 丁发兴, 倪鸣, 龚永智, 等. 栓钉剪力连接件滑移性能试验研究及受剪承载力计算[J]. 建筑结构学报, 2014, 35(9): 98−106. DING Faxing, NI Ming, GONG Yongzhi, et al. Experimental study on slip behavior and calculation of shear bearing capacity for shear stud connectors[J]. Journal of Building Structures, 2014, 35(9): 98−106.

[16] LIU X P, Bradford M A, Michael S S L. Behavior of high-strength friction-grip bolted shear connectors in sustainable composite beams[J]. Journal of Structural Engineering, 2015, 141(6): 1−12.

[17] Hassanieh A, Valipour H R, Bradford M A. Bolt shear connectors in grout pockets: Finite element modelling and parametric study[J]. Construction and Building Materials, 2018, 176: 179−192.

[18] YIN G A, DING F X, WANG H B, et al. Behavior of headed shear stud connectors subjected to cyclic loading[J]. Steel and Composite Structures, 2017, 25(6): 705−716.

[19] Abaqus[CP]. Version 6.12, 2012.

[20] DING F X, YING X Y, ZHOU L C, et al. Unified calculation method and its application in determining the uniaxial mechanical properties of concrete[J]. Frontiers of Architecture and Civil Engineering in China, 2011, 5(3): 381−393.

[21] 王燕, 郑杰, 侯兆欣. 高强螺栓外伸端板撬力作用的有限元分析与设计方法[J]. 建筑结构, 2009, 39(5): 68−75. WANG Yan, ZHENG Jie, HOU Zhaoxin. Design and finite element study on the prying force of high strength bolt in extended end-plate connections[J]. Building Structure, 2009, 39(5): 68-75.

[22] JGJ 82—2011, 钢结构高强螺栓连接技术规程[S]. JGJ 82—2011, Technical specification for high strength bolt connections of steel structure[S].

[23] GB 50017—2017, 钢结构设计设计标准[S]. GB 50017—2017, Standard for design of steel structures[S].

[24] ZHANG Y J, CHEN B C, LIU A R, et al. Experimental study on shear behavior of high strength bolt connection in prefabricated steel-concrete composite beam[J]. Composites Part B (2018), doi: https://doi.org/10. 1016/j.compositesb.2018. 10.007.

[25] 杜浩, 张冰, 胡夏闽, 等. 钢−混凝土组合梁螺栓连接件受剪性能试验研究[J]. 建筑结构学报, 2017(增1): 308−314. DU Hao, ZHANG Bing, HU Xiamin, et al. Experimental study on shear behavior of bolt connectors in steel- concrete composite beams[J]. Journal of Building Structures, 2017(Suppl 1): 308−314.

[26] ANSI/AISC 360-16, Specification for structural steel buildings[S]. Chicago, IL, 2016.

Shear bearing capacity of high-strength bolt connectors in steel-concrete composite beams

CHEN Jun1, WANG Wei1, DING Faxing2, 4, XU Fu1, LONG Shiguo1, YANG Caiqian1, 3

(1. College of Civil Engineering and Mechanics, Xiangtan University, Xiangtan 411105, China;2. College of Civil Engineering, Central South University, Changsha 410075, China;3. College of Civil Engineering, Southeast University, Nanjing 210018, China;4. Engineering Technology Research Center for Prefabricated Construction Industrialization of Hunan Province, Changsha 410075, China)

ABAQUS was used to develop the three-dimensional finite element model and study the shear bearing capacity of steel-concrete composite beams with high-strength bolt shear connector. The numerical model took into account the non-linearities of steel, concrete, bolt shear connector and other materials as well as contact among components. Validated against the experimental results, the structural performance of the high-strength bolt diameter, yield strength, length-diameter ratio and pretension as well as the strength of concrete was discussed. It was found that the shear bearing capacity was improved with the increase of concrete strength, high-strength bolt diameter and yield strength. The new design equation of single connector which considered the influence of concrete strength, diameter and yield strength was established through fitting. With then it comes to the comparison between numerical value under current specification of stud shear formula and numerical value calculated by high-strength bolt shear formula which was proposed by foreign scholars and this paper. The results show that the formula proposed in this paper is equipped with high precision.

steel-concrete composite beam; high-strength bolt shear connector; push-off test; FEA; shear bearing capacity

TU398.9

A

1672 − 7029(2019)10− 2553 − 09

10.19713/j.cnki.43−1423/u.2019.10.023

2018−12−25

国家重点研发计划项目(2017YFC0703404)；国家自然科学基金面上资助项目(51578548)；湖南省自然科学杰出青年基金资助项目(2019JJ20029)；湖南省科技重大专项(2017SK1010)；湖南省创新创业技术投资项目(2018GK5028)

丁发兴(1979−)，男，浙江瑞安人，教授，博士，从事钢−混凝土组合结构研究；E−mail：dinfaxin@mail.csu.edu.cn

(编辑 阳丽霞)