基于GA-BP的基坑施工引起隧道隆起变形预测研究

孟江，李慧民，田卫

基于GA-BP的基坑施工引起隧道隆起变形预测研究

孟江，李慧民，田卫

(西安建筑科技大学 土木工程学院，陕西 西安 710055)

通过遗传算法对BP神经网络的优化，结合郑州地铁1号线旁某深基坑工程施工的实际案例，建立深基坑施工引起邻近隧道隆起变形的预测模型，并通过MATLAB建模实现预测仿真。模型应用过程中利用“新陈代谢”的方法，根据实际监测情况不断调整样本数据，达到了实时预测的目的。研究结果表明：本文提出的预测模型对基坑施工过程中邻近隧道的隆起变形预测具有很高的准确性，并且对于不同的隧道截面具有很好的泛化能力，因此，对这类工程施工过程中，邻近隧道的安全运营具有一定的指导意义。

深基坑；隧道隆起变形；遗传算法；BP神经网络；预测

随着城市的不断扩张，交通网络的日益密集以及城市建设用地的日益稀缺，邻近地铁隧道时常会遇到基坑开挖工程，如广州地铁6号线旁某基坑工程[1]，杭州地铁2号线旁某深基坑开挖工程[2]，以及上海市地铁6号线旁浦东世纪大都会基坑工程[3]等。基坑的开挖会对下卧及周围土体产生卸载效应，打破邻近地层的应力平衡，进而导致土体产生回弹变形，而邻近既有地铁隧道即处于该回弹变形的地层当中，引起邻近既有隧道产生向上的隆起变形。另外，地铁的安全运营对隧道的变形要求非常高，绝对最大位移不能超过20 mm，隧道回弹变形不超过15 mm，隧道变形曲率半径必须大于15 000 m，相对变形必须小于1/2 500[4]，这就给该类基坑工程的施工带来很大的安全挑战，一方面，基坑施工过程中会对既有地铁隧道的周围土体产生影响，造成既有隧道的变形，引起地铁隧道的安全问题，而既有地铁在基坑施工的条件下正常使用会对基坑施工带来很大的挑战，加大施工难度，增加施工安全风险；另一方面，由于基坑工程与既有地铁隧道间存在不同的技术标准及管理模式，使得既有地铁隧道的存在对于基坑工程的施工来说不仅是重大的风险源，更是管理和技术上需要攻克的重点和难点。因此，对基坑施工过程中邻近地铁隧道的隆起变形发展有一个合理的预测，为采取控制措施赢得必要的准备时间显得非常重要。由于邻近基坑的开挖对隧道隆起变形的影响非常复杂，传统做法是通过一些基本假定，利用Mindlin弹性半空间应力解，进而通过弹性地基梁理论求算隧道隆起[5]。目前，很多学者主要通过数值模拟和实验来研究基坑开挖对隧道的影响[6−12]，也有学者通过对大量此类工程的统计分析，提出了基坑开挖引起隧道最大隆起变形的经验预测公式和预测模型[13]。这些方法虽然都可以对隧道隆起做一个预测，但并未实现实时预测隧道隆起变形的具体状况，而在邻近基坑施工过程中，需要及时了解隧道隆起变形的发展。BP神经网络具有很好的非线性及模糊推理能力，使其非常适合于作这种复杂的预测工作，且一些学者的研究表明将其应用于预测基坑开挖引起的地表沉降及基坑侧壁位移等变形是可行的[14]，但BP神经网络自身存在易陷入局部最优的问题，因此也有学者通过引入遗传算法或添加动量项等对BP神经网络进行优化[15]，取得了很好的效果。本文利用遗传算法对BP神经网络进行优化，在考虑基坑施工引起的隧道隆起变形具有滞后效应的情况下，建立基坑施工引起邻近既有地铁隧道隆起变形的预测模型，并在模型应用过程中引入“新陈代谢”的方法，以20 d的监测数据作为训练样本预测第21 d隧道的隆起变形，再根据隧道隆起变形实际状况不断调整样本数据，达到了实时预测的目的，且预测结果与监测结果吻合良好。因此，利用该方法可以提前实时的掌握隧道隆起发展状况，为采取控制措施赢得宝贵时间。

1 BP神经网络原理及构建

1.1 BP神经网络原理简介

BP神经网络应用非常广泛，其本质是一个多层感知器模型。通过训练数据的输入，利用输入层到隐含层再到输出层的计算处理和层层传递，得到输出结果，再将输出结果与期望输出对比，计算出网络的输出误差，再利用BP网络的误差反向传播功能，将误差从输出层依次反向传播到输入层，在反向传播过程中将误差分摊到各层的连接权值和阈值上，以此达到网络训练的目的，然后再进行下一次的输入和反向传播循环，直到输出误差小于精度要求或达到训练次数为止，完成网络的训练。最后即可利用训练好的网络实现识别和模拟等功能，其整个过程如图1所示。

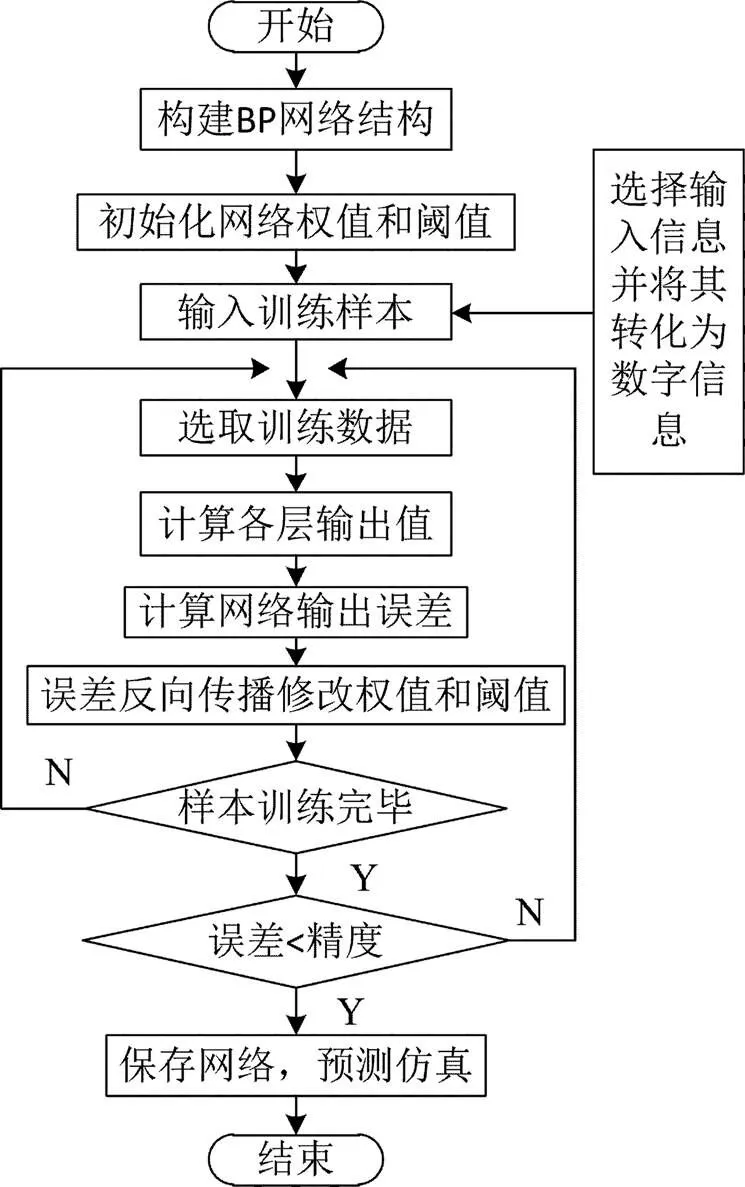
图1 神经网络训练流程图

1.2 BP神经网络构建

BP神经网络的设计主要包括输入层节点数、输出层神经元个数和隐含层层数以及各隐含层神经元个数的设计等。根据Kolmogorov定理，一个3层的神经网络即可以保证从任意n维到m维的复杂映射。因此，对于训练样本不大，输入层和输出层维数不多的情况下，采用一个3层的神经网络模型最为理想。本文即采用3层的网络结构。

对于输入层节点数和输出层神经元数设计，它分别和输入向量的维数以及输出向量的维数相对应，而对于隐含层神经元个数的设计，目前通常采用以下3种方法来初步确定[16]，再利用试算确定最合适的数目。

3)=log2，为输入层神经元个数。

2 遗传算法原理及实现

遗传算法是模仿生物遗传和进化而建立的一种优化算法，能够实现类似于生物优胜劣汰、适者生存的优选过程。利用遗传空间代替实际问题的解空间，以二进制编码为例(常见的编码方式有二进制编码、实数编码和格雷码编码)，利用一个二进制字符串代替实际问题的一个解，每个二进制字符串代表一个个体，二进制字符串的每一位代表一个基因，再根据实际问题的特点建立适应度函数，利用适应度函数计算出每一个个体的适应度值。遗传算法在实现过程中，首先随机产生一系列个体，将其称之为初始种群，初始种群通过复制、交叉和变异的遗传过程产生下一代，再利用适应度函数计算出的适应度值进行优选，使得适应度高的个体得以保留的几率大于适应度低的。通过每一代的遗传迭代使得实际问题的解得到不断优化，当达到精度要求时停止。最后将最优个体解码即得到满足精度要求的实际问题的最优解，实现流程如图2所示。

图2 遗传算法实现流程图

3 GA-BP网络预测模型建立

利用遗传算法强大的全局搜索能力对BP网络中初始化的权值和阈值进行优化，使得优化后的权值和阈值满足构建的适应度要求，再将优化后权值和阈值赋予BP网络，进行训练和预测仿真，整个实现过程如图3所示。

图3 GA优化BP网络的实施流程

4 案例

4.1 工程概况

郑州某广场项目设有南北2个矩形基坑，如图4所示，2个基坑分别位于地铁隧道两侧，基坑的设计大小为沿隧道总长177 m，宽110 m，深19.3 m，基坑长度范围内隧道顶最大埋深13.7 m，最小埋深8.7 m，基坑边线距隧道边的垂直距离为33 m。盾构隧道采用外径6 m，内径5.4 m，1.5 m宽，0.3 m厚，强度等级为C50的预制钢筋混凝土管片。南北2基坑同时施工，采用围护桩加锚索的支护方案，如图5所示。

图4 基坑平面布置图

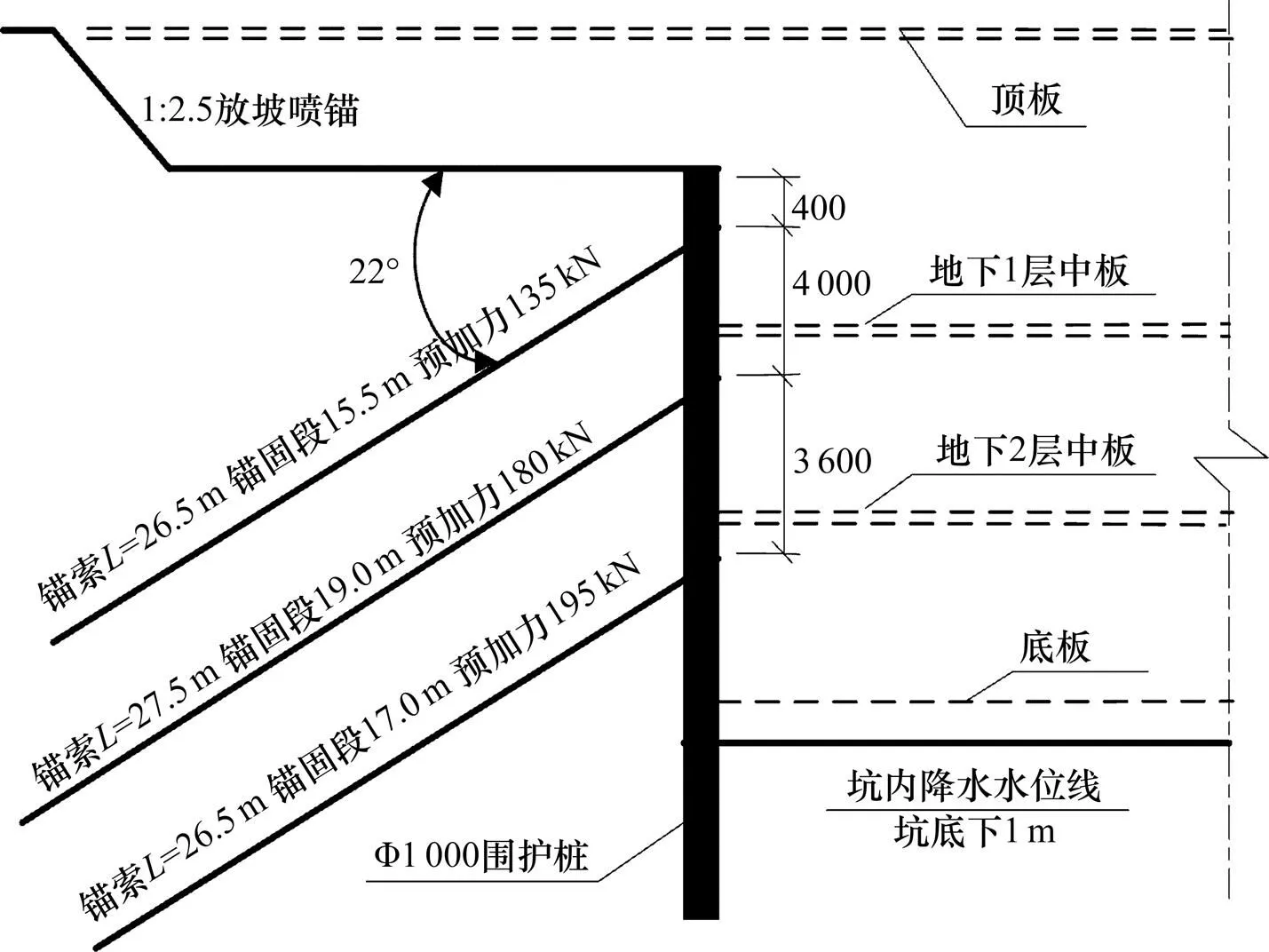
图5 基坑支护方案

工程范围内根据地质钻探结果和原位测试成果，勘探深度55 m深度以内除浅层部分杂填土外，主要为第4系全新统、上更新统冲积和冲洪积地层，揭露土层如下：①杂填土②粉土夹粉砂③粉质黏土④粉土夹粉质黏土⑤粉质黏土⑥细砂⑦粉质黏土⑧细砂⑨粉质黏土⑩细砂，其中地铁隧道位于第④⑤层。部分地质剖面图如图6所示。

勘探深度内含水层分为2层，即上层的潜水和下层的承压水。潜水主要赋存于16.0~18.0 m(绝对标高70.0 m)以上的粉土、粉质黏土中，属弱透水层；承压水主要赋存于16.0~18.0 m(绝对标高70.0 m)以下的细砂中，该层富水性好，属强透水层，具有微承压性，与上部潜水有一定水力联系。潜水层与承压水层被相对隔水层第5层粉质黏土层隔开。

4.2 GA-BP隧道隆起预测模型建立

在基坑施工过程中，影响隧道隆起变形的持续性变化因素主要有开挖基坑实时的几何尺寸以及开挖基坑边离隧道中线的距离，另外，由于基坑施工对隧道的变形影响具有滞后效应，因此基坑开挖的时间也是施工过程中影响隧道变形的一个持续性变化因素，本文将这些持续性变化因数作为模型的输入变量。由于隧道的变形随时间的推移而趋于稳定，因此时间变量(以天为单位)在输入模型前对其取对数处理更符合实际状况。对于在基坑施工过程中，影响隧道隆起变形的恒量因素，例如，土壤重度、摩擦角、黏聚力、压缩模量以及隧道埋深等，通过实时的隧道变形监测数据作为训练样本(教师信号)，以此将恒量因素对隧道变形影响的内在规律融入模型当中，减少人为干预。

图6 地质剖面图

图7 均方误差曲线图

利用1.2中2)的方法初步确定隐含层神经元数目在2~13之间，再通过试算确定最终数目(试算时采用4.3中模型网络训练的方法进行)。试算过程中计算得隐含层各神经元数目状况下对应预测结果的均方误差如图7所示，由图7可看出，隐含层神经元数目为13时均方误差最小，精度最高，因此确定隐含层神经元个数为13，从而可得预测模型的BP网络拓扑结构如图8。再将遗传算法部分接入BP网络，设置进化代数为65代，种群规模为30，交叉概率为0.2，变异概率为0.05，最后形成一个完整的预测模型。

图8 BP神经网络拓扑结构

4.3 模型网络训练

通过连续20 d基坑开挖的实际数据作为训练样本，包括这20 d中每天基坑的实际几何尺寸、基坑边距隧道中线的距离以及基坑已开挖的时间，利用对应时间的隧道隆起变形实际监测数据作为教师信号，以此对模型网络进行训练，再利用训练好的网络预测隧道在第21 d时的隆起状况。最后通过新陈代谢的方法不断向前推进，即依次利用前20 d的监测数据预测下一天的隧道隆起变形情况。整个预测推进过程如图9所示。

本文选取隧道断面DM7，DM15和DM23进行预测，3个隧道断面分别位于基坑两端和中部，隧道断面分部如图10所示。

图10中每个断面均设有监测点，断面间的间距为5~10 m。通过施工过程中隧道断面DM15处隧道隆起实际监测数据与预测数据对比，分析模型的预测能力；利用隧道断面DM7及断面DM23的预测数据与监测数据对比，分析预测模型的泛化能力；利用不经遗传算法优化的BP神经网络预测隧道DM15断面的隆起情况，并与经过遗传算法优化的BP神经网络预测结果对比，分析遗传算法对该预测模型的优化能力。

图9 循环推进预测流程图

图10 隧道断面分布图

4.4 隧道隆起预测结果分析

将隧道断面DM15的80组监测数据与预测数据对比，得到预测绝对误差均在0.5 mm范围以内，最大误差为−0.29 mm，相对误差均在6%以内，最大相对误差为5.22%，预测数据与监测数据对比如图11所示，误差曲线如图12所示。对比结果表明，模型预测精度满足要求。

为测试该模型对相对于基坑不同位置的隧道断面的预测能力，再将隧道隆起预测模型用于预测隧道断面DM7和DM23的隆起情况，并将预测结果与监测结果对比，得到预测绝对误差均在0.6 mm以内，最大误差为−0.6 mm，相对误差均在10%以内，最大相对误差为8.82%。2个断面的预测数据与监测数据对比如图13~14所示，误差曲线如图15所示。

图11 断面DM15预测数据与监测数据对比

图12 断面DM15预测误差曲线

图13 断面DM7预测数据与监测数据对比

由图15可看出，模型对于不同隧道断面都具有较好的预测精度，并且均没有出现过度拟合现象。体现出模型具有较好的泛化能力。

图14 断面DM23预测数据与监测数据对比

图15 断面DM7和DM23预测误差曲线

将经过遗传算法优化的模型和未经过遗传算法优化的模型同时用于预测相同隧道断面的隆起情况，其中断面DM15预测结果部分如表1所示。优化后的模型预测绝对误差最大为−0.29 mm，相对误差大于5%的有2组，占总数的2.5%，相对误差在2%~5%之间的有27组，占总数的33.75%，有63.75%的误差在2%范围以内；而对于未优化的模型，预测绝对误差最大为−0.76 mm，相对误差大于5%的有16组，占总数的20%，相对误差在5%~2%之间的有30组，占总数的37.5%，小于2%的只占42.5%。可见，由于BP神经网络预测模型的初始权值和阈值为随机给定，在训练过程当中，一部分隧道截面收敛于极值点(局部最优点)而非最值点(全局最优点)，即便其中一些极值点仍在可接受范围内，但其精度与最值点相比并非最优。而通过遗传算法优化的模型在预测过程中，利用遗传算法对初始权值和阈值进行预先处理，遗传算法强大的全局搜索能力使其跳过了易陷入的局部最优点，故而精度大大提高。

在基坑开挖过程中，工程技术人员需要及时了解的不仅仅是某个隧道断面的隆起状况，而是整个基坑影响范围内邻近既有地铁隧道的隆起变形情况，因此，将上述建立的优化预测模型用于预测该基坑长度范围内的隧道段隆起变形情况，以检验预测模型的实用性。现将模型用于预测基坑开挖到第80 d时的隧道隆起变形情况，如图16所示。

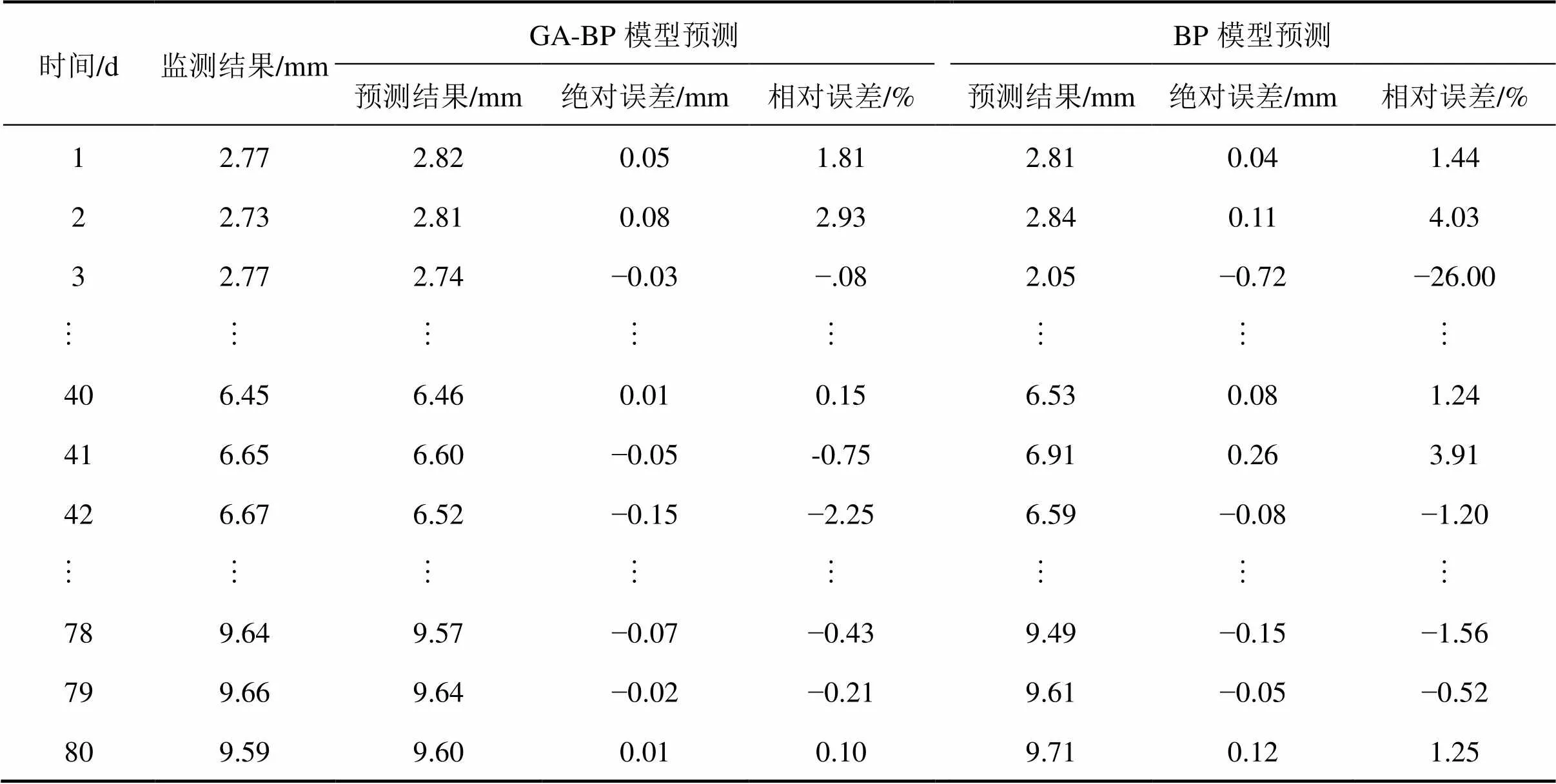
表1 断面DM15预测结果与监测结果对比

图16 基坑长度范围内隧道隆起变形预测

由图16可看出，预测结果与实际监测结果在整个隧道段吻合良好，可在第79 d提醒工程技术人员采取合理控制措施，以防断面DM21附近处隧道隆起变形继续增加。

5 结论

1) 通过遗传算法优化神经网络建立隧道隆起预测模型，并利用该模型来预测既有隧道邻近基坑施工过程中的隆起变形状况，该方法对于这类工程的预测精度高、收敛快，可用于实时预测基坑施工过程中隧道的隆起变形状况，为保证既有隧道的运营安全及时采取控制措施赢得必要的准备时间，具有较好的实用性。

2) 在邻近基坑施工过程中，引起隧道变形的因素很多，其中的一些因素在整个工程施工过程中不断变化，而另外一些影响因素几乎保持不变，可通过将主要的持续变化的因素作为输入训练样本、将实际监测数据作为教师信号，以此兼顾变化的因素和恒定的因素，减少人为干预，从而能够有效的反应引起隧道变形的内在规律。

3) 采用新陈代谢的预测方法能够实现有效的实时预测，若将预测的时间在有效精度范围内向前推进到2 d，3 d甚至更长将会有更好的实用性。

[1] 冯龙飞, 杨小平, 刘庭金. 紧邻地铁侧方深基坑支护设计及变形控制[J]. 地下空间与工程学报, 2015, 11(6): 1581−1587. FENG Longfei, YANG Xiaoping, LIU Tingjin. Supporting design and deformation control of deep excavation adjacent to the metro side[J]. Chinese Journal of Underground Space and Engineering, 2015, 11(6): 1581−1587.

[2] 魏纲, 厉京, 宣海力, 等. 大型深基坑开挖对旁边地铁盾构隧道影响的实测分析[J]. 铁道科学与工程学报, 2018,15(3): 718−726. WEI Gang, LI Jing, XUAN Haili, et al. Monitoring data analysis on the influence of large deep foundation pit excavation on nearby metro shield tunnel[J]. Journal of Railway Science and Engineering, 2018, 15(3): 718−726.

[3] 肖潇, 李明广, 夏小和, 等. 基坑开挖对临近明挖暗埋隧道竖向变形的影响机理[J]. 上海交通大学学报, 2018, 52(11): 1437−1443. XIAO Xiao, LI Mingguang, XIA Xiaohe, et al. Mechanism of foundation pit excavation on vertical deformation of closed open-buried tunnels[J]. Journal of Shanghai Jiaotong University, 2018, 52(11): 1437−1443.

[4] 刘国彬, 黄院雄, 侯学渊. 基坑工程下已运行地铁区间隧道上抬变形的控制研究与实践[J]. 岩石力学与工程学报, 2001, 20(2): 202−207. LIU Guobin, HUANG Yuanxiong, HOU Xueyuan. Study and practice of control of uplift deformation of metro tunnels under foundation pit engineering[J]. Chinese Journal of Rock Mechanics and Engineering, 2001, 20(2): 202−207.

[5] 陈郁, 李永盛. 基坑开挖卸荷引起下卧隧道隆起的计算方法[J]. 地下空间与工程学报, 2005, 1(1): 91−94. CHEN Yu, LI Yongsheng. Calculation of tunnel heaving due to unloading of pit excavation[J]. Chinese Journal of Underground Space and Engineering, 2005, 1(1): 91−94.

[6] Ng C W W,SHI Jiangwei, Masin,et al. Influence of sand density and retaining wall stiffness on three-dimensional responses of tunnel to basement excavation[J]. Canadian Geotechnical Journal, 2015, 52(11): 1811−1829 .

[7] SHI Chenghua, CAO Chengyong, LEI Mingfeng, et al. Effects of lateral unloading on the mechanical and deformation performance of shield tunnel segment joints[J]. Tunnelling and Underground Space Technology, 2016, 51: 175−188.

[8] LI Mingguang, ZHANG Zhongjie, CHEN Jinjian, et al. Zoned and staged construction of an underground complex in Shanghai soft clay[J]. Tunnelling and Underground Space Technology, 2017, 67: 187−200.

[9] SUN Qian, YAN Changhong, QIU Jianfei, et al. Numerical simulation of a deep excavation near a shield tunnel[J]. Tehnicki Vjesnik-Technical Gazette, 2018, 25(3): 670−678 .

[10] CHEN Renpeng, MENG Fanyan, LI Zhongchao, et al. Investigation of response of metro tunnels due to adjacent large excavation and protective measures in soft soils[J]. Tunnelling and Underground Space Technology, 2016, 58: 224−235.

[11] 黄宏伟, 黄栩, Schweiger F Helmut. 基坑开挖对下卧运营盾构隧道影响的数值模拟研究[J]. 土木工程学报, 2012, 45(3): 182−189. HUANG Hongwei, HUANG Xu, Schweiger F Helmut. Numerical analysis of the influence of deep excavation on underneath existing road tunnel[J]. China Civil Engineering Journal, 2012, 45(3): 182−189.

[12] 郑刚, 杜一鸣, 刁钰, 等. 基坑开挖引起邻近既有隧道变形的影响区研究[J]. 岩土工程学报, 2016, 38(4): 599−612.ZHENG Gang, DU Yiming, DIAO Yu, et al. Influenced zones for deformation of existing tunnels adjacent to excavations[J]. Chinese Journal of Geotechnical Engineering, 2016, 38(4): 599−612.

[13] 魏纲. 基坑开挖对下方既有盾构隧道影响的实测与分析[J]. 岩土力学, 2013, 34(5): 1421−1428. WEI Gang. Measurement and analysis of the influence of foundation pit excavation on existing shield tunnels below[J]. Rock and Soil Mechanics, 2013, 34(5): 1421− 1428.

[14] CAO M S, PAN L X, GAO Y F, et al. Neural network ensemble-based parameter sensitivity analysis in civil engineering systems[J]. Neural Computing & Applications, 2017, 28(7): 1583−1590.

[15] DING Shifei, ZHANG Yanan, CHEN Jinrong, et al. Research on using genetic algorithms to optimize Elman neural networks[J]. Neural Computing & Applications, 2013, 23(2): 293−297.

[16] 陈明. MATLAB神经网络原理与实例精解[M]. 北京: 清华大学出版社, 2013. CHEN Ming. Principles and examples of MATLAB neural network[M]. Beijing: Tsinghua University Press, 2013.

Prediction of tunnel uplift deformation caused by foundation pit construction based on GA-BP

MENG Jiang, LI Huimin, TIAN Wei

(School of Civil Engineering, Xi’an University of Architecture and Technology, Xi’an 710055, China)

The construction of the deep foundation pit cause the uplift deformation of the adjacent subway tunnel, which bring great security risks to the operation of the subway. This paper optimized BP neural network by genetic algorithm. In combined with the actual case about construction of a deep foundation pit next to Zhengzhou Metro Line 1, it was established to the prediction model of the adjacent tunnel uplift deformation caused by deep foundation pit construction, and the prediction simulation was realized by MATLAB modeling. In the process of model application, the “metabolism” method was used to continuously adjust the sample data according to the actual monitoring situation, achieving the purpose of real-time prediction. The results show that the prediction model proposed in this paper has high accuracy for predicting the uplift deformation of adjacent tunnels during deep foundation pit construction and has good generalization ability for different tunnel sections. Therefore, it has certain guiding significance for the safe operation of adjacent tunnels in the construction process of such projects.

deep foundation pit; tunnel uplift deformation; genetic algorithm; BP neural network; prediction

TU94+1

A

1672 − 7029(2019)10− 2521 − 09

10.19713/j.cnki.43−1423/u.2019.10.019

2018−12−13

住建部科技项目(2015-R3-003)

李慧民(1954−)，男，陕西澄城人，教授，从事土木工程建造与管理的研究；E−mail：li_huimin2005@126.com

(编辑 阳丽霞)