褶皱效应对新型组合箱梁力学特性的影响研究

张紫辰，王根会

褶皱效应对新型组合箱梁力学特性的影响研究

张紫辰1，王根会2

(1.兰州交通大学 甘肃省道路桥梁与地下工程重点实验室，甘肃 兰州 730070；2. 兰州交通大学 土木工程学院，甘肃 兰州 730070)

针对新型组合箱梁受腹板褶皱效应的影响，力学特性发生较大变化的问题，采用模型试验和数值模拟的方法对这一现象进行研究。通过制作模型试验梁，并测试其一阶竖向振动频率和在不同荷载作用下跨中翼板应力值，建立ANSYS有限元模型对试验值进行验证；运用有限元软件分析高跨比、波纹腹板厚度和波折角对组合箱梁动力特性的影响。研究结果表明：模型试验值与有限元解吻合良好，褶皱效应对组合箱梁下翼板的应力影响最大，达到15%~21%左右；增大腹板厚度能有效提高组合箱梁总体刚度；增大腹板波折角对结构竖向和横向振动频率影响较小，但对其扭转振动频率影响较大；组合箱梁扭转振动频率的增大幅度随其高度的增加逐渐减小。

组合箱梁；褶皱效应；模型试验；有限元；动力特性

新型组合箱梁是传统波纹钢腹板组合箱梁下翼板(RC板)被平钢板所置换的一种新型结构。该类结构充分利用了混凝土顶板抗压，钢底板抗拉，以及波形钢腹板抗剪屈服强度高的特点。实际上传统波纹钢腹板组合箱梁是20世纪末出现的一种组合结构[1−4]，由于其自重轻，预应力效率高，具有良好的力学性能有效解决了温度应力和收缩、徐变等因素带来的结构病害[5−7]。自从1986年法国建成世界上第一座波纹钢腹板组合箱梁桥—Cognac桥，世界上已建波纹钢腹板组合箱梁桥达300余座，而我国已建和在建该类桥梁近40余座[8−11]。然而，这种传统波纹钢腹板组合箱梁在正弯矩作用下，混凝土底板受拉，需要张拉较多的预应力束，施工较为复杂。近年来，我国桥梁工作者又有新的发现，为了提高施工进度、进一步减轻结构自重，以及增强桥梁结构的抗震性能，进而提出了新型波纹腹板组合箱梁的设计。但是，由于该类结构的质量主要集中在组合箱梁顶板，故引起其中性轴上移。与传统组合箱梁相比较，腹板褶皱效应对新型组合结构力学行为的影响差异较大。因此，该类组合结构腹板褶皱效应的研究变得更为重要。为此制作了新型波纹腹板组合箱梁模型，对其进行静力加载试验，并测试组合箱梁跨中翼板应力值和竖向一阶振动频率，建立有限元模型模拟试验加载过程，对比分析试验值和计算值的差异；然后运用所建立的有限元模型系统分析褶皱效应对新型组合箱梁动力特性的影响，以期为组合箱梁的相关力学特性研究提供科学的理论依据。

1 建立组合箱梁有限元模型

新型波纹腹板组合箱梁如图1所示。其截面尺寸为：混凝土翼板宽1 100 mm，厚度55 mm，钢底板宽500 mm，厚度4 mm，波纹钢腹板高405 mm，腹板厚度3 mm，波长144 mm，波折角37°，水平面板宽40 mm，波形高度24 mm。波纹平面示意如图2所示。

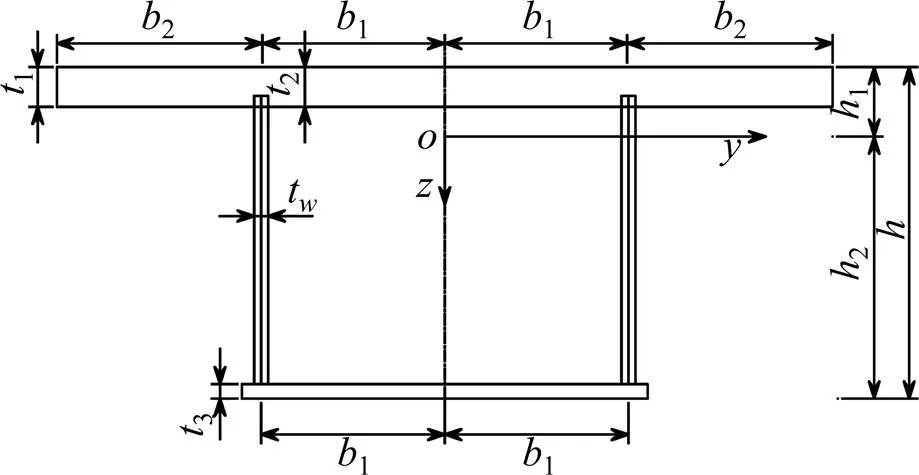
图1 新型波纹钢腹板组合箱梁

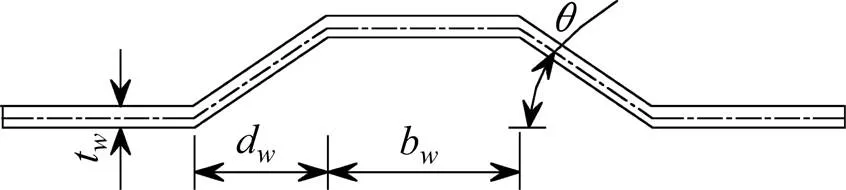
图2 波纹钢腹板示意图

(a) 组合箱梁有限元模型；(b) 钢腹板和横隔板网格划分

利用ANSYS有限元软件建立简支新型波纹腹板组合箱梁模型如图3(a)所示，其中C50混凝土选用SOLID65单元模拟，Q390钢板选用SHELL63模拟[12−13]，考虑到钢混连接部位要使用MPC方式，增加目标单元TARGE170和接触单元CONTA175。波纹钢腹板和钢横隔板的网格划分如图3(b)所示。

2 室内模型试验

2.1 模型梁静力加载试验

为验证本文所建立的新型波纹腹板组合箱梁有限元模型的准确性，制作2.6 m等截面简支组合箱梁的模型试验梁，其计算跨径为2.45 m，对模型梁进行静力加载试验，采用跨中集中荷载和满跨均布荷载两种方式进行，计算时集中荷载取=10 kN，均布荷载取=2.79 kN/m。

1) 模型试验梁均布荷载加载工况

首先用铁块分层摊铺，每层均匀放置33块，因数量有限，3层铁块放完后，用沙袋均匀摊铺。

2) 模型试验梁集中荷载加载工况

在跨中腹板对应的顶板上方加垫块，再调平垫块，保证集中力相等施加在跨中两侧腹板上方，加载时0~6 kN按每次1 kN的递增方式，6~10 kN按0.5 kN的递增方式。

把试验所得翼板应力值与有限元结果列入表1进行对比。

表1 简支组合箱梁跨中截面翼板应力值

从表1可以看出，在不同荷载作用下，通过本文所建立的有限元模型得到的组合箱梁跨中截面翼板应力值与室内模型试验值吻合良好，说明本文所建立的有限元模型是合理的。

2.2 模型梁振动频率测试

为测试模型梁的振动频率，分别在主梁1/4跨、2/4跨和3/4跨放置拾振器。

将实测组合箱梁一阶竖向振动频率与有限元计算结果列入表2进行对比。

表2 振动频率对比

从表2可以看出，实测组合箱梁一阶竖向弯曲振动频率与有限元计算结果基本吻合，相对误差为4.38%，由此可知，本文建立的新型波纹腹板组合箱梁有限元分析模型是合理的。同时在实际测试中发现，由于模型梁的刚度过大及横向支撑的不确定性，导致通过室内试验的方法难以采集到更多与频率相关的数据。所以建议今后的试验应适当减小模型截面尺寸，增大梁的跨度，从而减小其刚度以方便仪器测量。

3 褶皱效应对箱梁力学特性的影响

从前面的分析可知，有限元法模拟精度良好，因而可以利用它对新型波纹腹板组合箱梁的力学特性进行研究。本文基于试验模型梁主要分析褶皱效应对组合箱梁翼板应力、竖向振动频率和竖向挠度的影响，由于模型梁跨度较小，同时主要研究腹板形状变化对组合箱梁力学特性的影响，所以在利用ANSYS有限元软件分析时忽略腹板质量的 变化。

3.1 褶皱效应对组合箱梁翼板应力的影响

根据本文建立的波纹腹板和相同截面尺寸的平钢腹板组合箱梁有限元模型，分析不同荷载作用下2种简支组合箱梁跨中截面翼板应力的变化情况，结果如图4所示。

从图4可以看出，不同荷载作用下，2种组合箱梁上下翼板都出现了明显的剪力滞效应，且变化规律基本保持一致。不同荷载作用下，波纹腹板组合箱梁跨中上翼板正应力均小于平钢腹板组合箱梁，下翼板正应力变化规律与上翼板相反。由于褶皱效应的存在，使得组合箱梁上翼板应力变化了0.3%~1%左右；褶皱效应对组合箱梁下翼板的影响更加显著，使下翼板应力增大了15%~21%左右。

(a) 上翼板；(b) 下翼板

3.2 褶皱效应对组合箱梁竖向振动频率的影响

根据本文建立的2种组合箱梁有限元模型，通过分析计算，得到各自的主梁一阶竖向振动频率，并将计算结果列入表3进行对比。

从表3可以看出，波纹腹板组合箱梁的一阶竖向振动频率小于平钢腹板组合箱梁，说明受褶皱效应的影响，波纹腹板钢底板组合箱梁竖向刚度明显减小。

3.3 褶皱效应对组合箱梁竖向挠度的影响

根据本文建立的2种组合箱梁有限元模型，计算简支组合箱梁在跨中集中荷载作用下的竖向挠度，结果如图5所示。

表3 主梁一阶竖向振动频率对比

图5 集中荷载下2种腹板形式组合箱梁竖向挠度

从图5可以看出，波纹腹板组合箱梁在跨中集中荷载作用下的竖向挠度大于平钢腹板组合箱梁，褶皱效应对组合箱梁竖向挠度的影响保持在8.5%左右。

4 组合箱梁褶皱效应的影响因素

由于影响新型波纹腹板组合箱梁褶皱效应的因素较多，本文着重研究波纹钢腹板厚度和腹板波折角对组合箱梁动力特性的影响，以此来反映其各向刚度受褶皱效应的影响程度[14]。为使组合箱梁在自由振动时出现需要研究的振动模态，利用ANSYS有限元软件建立跨径为30 m的简支组合箱梁，其中梁高=2.25 m，1=2=25 cm，3=2.5 cm，1=2=2 m。

4.1 波纹腹板厚度的影响

以本文建立的30 m跨径组合箱梁有限元模型为基础，变化波纹腹板厚度t=10~18 mm，保持波折角=37°和其他结构参数不变，则新型波纹腹板组合箱梁的竖向、横向和扭转一阶振动频率随腹板厚度的变化情况如表4所示。

从表4可以看出，随着腹板厚度的增加，组合箱梁的竖向一阶振动频率、横向一阶振动频率和扭转一阶振动频率均逐渐增大，其中扭转一阶振动频率增大速率最快，说明增加波纹腹板厚度有助于提高箱梁的整体刚度，特别是扭转刚度得到了很大提升；但当t增大到一定程度时，其对组合箱梁刚度提升的影响逐渐减小。所以工程实际中应结合经济性对比选择合适的腹板厚度。

表4 不同腹板厚度下组合箱梁振动频率

单独研究高跨比下不同波纹腹板厚度组合箱梁扭转振动的变化情况，将各因素影响下组合箱梁扭转频率进行对比，如图6所示。

图6 各因素对组合箱梁扭转振动的影响对比

从图6可以看出，随着高跨比的增大，不同波纹腹板厚度组合箱梁的扭转振动频率呈递增趋势，但当高跨比增大到一定程度时，扭转振动频率增幅逐渐减小。

4.2 波纹腹板波折角的影响

以本文建立的30 m跨径组合箱梁有限元模型为基础，结合工程实际选取波纹腹板波折角27°~60°，保持波纹腹板厚度t=12 mm和其他结构参数不变，则组合箱梁的竖向、横向和扭转一阶振动频率随腹板波折角的变化情况见表5(表中的振动频率为不考虑钢腹板质量的情况下，组合箱梁在不同腹板波折角下的值)[15]。

表5 不同腹板波折角下组合箱梁振动频率

从表5可以看出，随着腹板波折角的增加，组合箱梁的竖向一阶振动频率逐渐减小，说明增大波折角会减小组合箱梁的竖向抗弯刚度；横向一阶振动频率随波折角增大而增大，但变化幅度较小；扭转一阶振动频率随波折角增大而减小，变化幅度较大，说明当腹板波折角在27°~60°之间变化时，组合箱梁扭转刚度有所减小。

5 结论

1) 褶皱效应对新型组合箱梁竖向抗弯刚度和翼板应力值影响较大。在集中荷载作用下，对其竖向挠度的影响保持在8.5%左右，对下翼板应力的影响最为突出，达到15%~21%。

2) 适当增大腹板厚度，有助于提高组合箱梁的整体刚度，但当其增大到一定程度时，对箱梁刚度提升的贡献会降低；随着腹板波折角增大，组合箱梁的竖向抗弯刚度和扭转刚度减小，横向刚度增大；组合箱梁扭转振动频率的增大幅度随其高度的增加逐渐减小。所以，该方面问题应该引起结构设计者的特别关注。

3) 运用本文建立的有限元模型计算得到的组合箱梁竖向一阶振动频率和不同荷载作用下跨中翼板应力值与室内模型试验值吻合良好，说明本文建立的有限元模型是合理的，同时也印证了室内模型试验方法的正确性。因而，本文所得结论对该类组合箱梁的设计具有指导意义。

[1] 周勇超, 郝宪武, 李子青. 变截面波形钢腹板组合梁剪力滞效应[J]. 长安大学学报(自然科学版), 2014, 7(4): 62−69. ZHOU Yongchao, HAO Xianwu, LI Ziqing, et al. Shear lag effect of non-uniform composite beam with corrugated steel web[J]. Journal of Chang’an University (Natural Science Edition), 2014, 7(4): 62−69.

[2] Basher M, Shanmugam N E, Khalim A R. Horizontally curved composite plate girders with trapezoidally corrugated webs[J]. Journal of Constructional Steel Research, 2011, 67: 947−956.

[3] Leblouba M, Junaid M T, Barakat S, et al. Shear buckling and stress distribution in trapezoidal web corrugated steel beams[J]. Thin Wall Struct, 2017, 113: 13−26.

[4] 马驰, 刘世忠, 冀伟, 等. 单箱多室波形钢腹板PC组合箱梁剪力滞效应研究[J]. 公路交通科技, 2018, 35 (2): 62−78. MA Chi, LIU Shizhong, JI Wei, et al. Study on shear lag effect of single box multi-cell PC composite box girder with corrugated steel webs[J]. Journal of Highway and Transportation Research and Development, 2018, 35(2): 62−78.

[5] 吴文清, 万水, 叶见曙, 等. 波形钢腹板组合箱梁剪力滞效应的空间有限元分析[J]. 土木工程学报, 2004, 37(9): 31−36. WU Wenqing, WAN Shui, YE Jianshu, et al. 3-D finite element analysis on shear lag effect in composite box girder with corrugated steel web[J]. China Civil Engineering Journal, 2004, 37(9): 31−36.

[6] Hassanein M F, Kharoob O F. Shear buckling behavior of tapered bridge girders with steel corrugated webs[J]. Engineering Structures, 2014, 74: 157−169.

[7] 胡华万, 李俊, 强士中. 波形钢腹板PC组合箱梁剪切屈曲性能研究[J]. 铁道工程学报, 2011(2): 80−83. HU Huawan, LI Jun, QIANG Shizhong. Study on shear buckling property of corrugated steel web PC combined box girder[J]. Journal of Railway Engineering Society, 2011(2): 80−83.

[8] 马驰, 刘世忠, 伍明强. 考虑剪切剪滞双重效应波形钢腹板组合箱梁的矩阵分析[J]. 中国公路学报, 2018, 31(3): 80−88. MA Chi, LIU Shizhong, WU Mingqiang. Matrix analysis of composite box girder with corrugated steel webs considering shear deformation and shear lag effect[J]. China Journal of Highway and Transport, 2018, 31(3): 80−88.

[9] 聂建国, 朱力, 唐亮. 波形钢腹板抗剪强度[J]. 土木工程学报, 2013, 46(6): 97−109. NIE Jianguo, ZHU Li, TANG Liang. Shear strength of trapezoidal corrugated steel webs[J]. China Civil Engineering Journal, 2013, 46(6): 97−109.

[10] 李立峰, 侯立超, 孙君翠. 波形钢腹板抗剪性能研究[J]. 湖南大学学报(自然科学版), 2015, 42(11): 56−63. LI Lifeng, HOU Lichao, SUN Juncui. Research on shear mechanical property of corrugated steel webs[J]. Journal of Hunan University (Natural Science), 2015, 42(11): 56−63.

[11] YI Jongwon, Heungbae Gilb, Kwangsoo Yonm, et al. Interactive shear buckling behavior of trapezoidally corrugated steel webs[J]. Engineering Structures, 2008, 30: 1659−1666.

[12] 宋随弟, 祝兵, 陈克坚, 等. 不考虑滑移时波形钢腹板箱梁受力性能研究[J]. 铁道工程学报, 2014(6): 50−55. SONG Suidi, ZHU Bing, CHEN Kejian, et al. Mechanical performance research on the box girder with corrugated steel webs without considering slippage[J]. Journal of Railway Engineering Society, 2014(6): 50−55.

[13] 林梦凯, 冀伟, 李海莲, 等. 波形钢腹板工字型钢梁的手风琴效应研究[J]. 铁道科学与工程学报, 2016, 13(2): 283−288. LIN Mengkai, JI Wei, LI Hailian, et al. Study on accordion effect of corrugated steel webs i-shaped steel girde[J]. Journal of Railway Science and Engineering, 2016, 13(2): 283−288.

[14] 陈海波, 刘保东, 任红伟. 波纹钢腹板混凝土箱梁动力特性研究[J]. 公路交通科技, 2007, 24(2): 80−83. CHEN Haibo, LIU Baodong, REN Hongwei. Research on dynamic characteristic of concrete box girder with corrugated steel webs[J]. Journal of Highway and Transportation Research and Development, 2007, 24(2): 80−83.

[15] 郑尚敏. 波形钢腹板PC组合箱梁桥动力性能研究[D]. 南京: 东南大学, 2016. ZHENG Shangmin. Research on dynamic performance of PC composite box gieder bridge with corrugated steel webs[D]. Nanjing: Southeast University, 2016.

Study on the influence of folding effect on the mechanical characteristics of new composite box girder

ZHANG Zichen1, WANG Genhui2

(1. Lanzhou Jiaotong University, Key Laboratory of Road & Bridge and Underground Engineering of Gansu Province, Lanzhou 730070, China; 2. School of Civil Engineering, Lanzhou Jiaotong University, Lanzhou 730070, China)

The mechanical properties of the composite box girder have undergone great changes due to the influence of the webs fold effect. This paper used model test and numerical simulation to study this phenomenon. The model test beam was fabricated, tested the first-order vertical vibration frequency and the stress value of the mid-span plate under different loads. The ANSYS finite element model was established to verify the test values. The finite element software was used to analyze the influence of high-span ratio, corrugated web thickness and wave-angle angle on the dynamic characteristics of composite box girder. The results show that the model test value is in good agreement with the finite element solution. The fold effect has the greatest influence on the stress of the lower wing of the composite box girder, which is about 15%~21%. Increasing the corrugated web thickness can effectively improve the overall stiffness of the composite box girder; Increasing the web corner angle has little effect on the vertical and lateral vibration frequencies of the structure, but it has a great influence on the torsional vibration frequency. Increasing the combined beam height will reduce the influence of the fold effect on the torsional vibration. The increase amplitude of the torsional vibration frequency of the composite box girder decreases with the increase of its height.

composite box girders; fold effect; model test; finite element; dynamic characteristic

U448.27

A

1672 − 7029(2019)10− 2491 − 06

10.19713/j.cnki.43−1423/u.2019.10.015

2018−11−29

国家自然科学基金资助项目(51368035)；甘肃省交通厅项目(2016-34)

王根会(1962−)，男，陕西礼泉人，教授，博士，从事桥梁结构理论、桥梁健康诊断方面研究；E−mail：wahl@mail.lzjtu.cn

(编辑 涂鹏)