抗拔支盘桩首盘深度与抗拔力的关系研究

杨治军，谢永利，范祥，刘毅鑫

抗拔支盘桩首盘深度与抗拔力的关系研究

杨治军，谢永利，范祥，刘毅鑫

(长安大学 公路学院，陕西 西安 710064)

基于岩土弹塑性本构关系的数值计算理论，运用ABAQUS有限元软件，建立桩土轴对称模型。在指定桩顶位移条件下，分析支盘桩抗拔承载力的变化情况，得到首盘深度对支盘桩抗拔承载力的影响规律。研究结果表明：对于不同首盘深度的支盘桩，随着桩顶位移的逐步增加，在未达到极限抗拔荷载值之前，其抗拔承载力随着首盘深度的增大而减小，在达到极限抗拔荷载之后，其抗拔承载力随着首盘深度增加而增大；对于长度不同的支盘桩，首盘深度值为桩长(双盘桩为总桩长、三盘桩为次盘深度)的24%~30%时，抗拔承载力达到最大；在最优首盘深度的条件下，无论支盘数目多少，当桩周土为黏土且处于饱和状态，支盘桩的单位桩长所提供的抗拔承载力，相比于直桩提高了7.5%，结果可为实际工程中支盘桩的长度设计提供理论支撑。

有限元模拟；支盘桩；抗拔承载力；首盘深度；上拔荷载-位移曲线

抗拔桩在大型地下室抗浮、高耸建(构)筑物与海上码头平台抗拔、悬索桥和斜拉桥的基础锚桩、大型船坞地板的桩基础和静上拔荷载试桩中的锚桩基础均有应用。工程上的抗浮或抗拔通常采用压重法、抗浮锚杆、普通等截面抗拔桩等措施，同时，传统的抗拔工程措施存在诸多不足，压重法利用增加结构的自重以平衡地下水的上浮力，但经济成本高，抗浮锚杆利用锚杆和砂浆组成的锚固体与岩土层的结合力作为抗浮力，但易受地质条件影响，承载力不稳定，普通等截面桩的基础抗拔力是由桩侧摩擦阻力及桩身自重所提供，但造价较高，抗拔力较小。支盘桩随即应运而生，它在传统抗拔桩的基础上，通过在桩身设置支盘，使得抗拔桩不仅有桩侧表面摩擦提供抗拔力，而且变截面处的承力支盘，也扩大了桩−土间的接触面积，最重要的是可以在桩体设置多个支盘，与扩底桩相比大大增加了端承面积，提供了较大的端承抗拔阻力，并能充分利用盘顶以上土体的自重，因而具有很好的抗拔性能，并且其抗拔承载力十分稳定，施工方法也比较成熟。近些年来，诸多学者对支盘桩的竖向受力特性和支盘设计进行了深入研究。范孟华等[1]通过分析相邻两盘间的破坏面形态，推导出基于小抗力的支盘桩承载力和临界盘间距计算公式。夏红兵等[2]利用FLAC3D数值软件，模拟盘间距、盘数量和盘径对新型扩挤支盘桩竖向承载力影响规律，得出最优的盘间距、盘数量和盘径。陆凤池等[3]利理论推导旋扩珠盘桩临界盘间距，通过数值模拟验证并分析了不同盘间距的承力盘端阻力、桩侧摩阻力、桩端阻力的变化规律。卢成原等[4]通过室内模型试验，研究不同土质中支盘桩单桩的合理盘间距，得出不同土质条件下的合理盘间距。卢成原等[5]通过室内模型试验，确定出最优的不同形状盘体组合。KE等[6]建立三维有限元模型分析出支盘桩承载力主要取决于板的下坡和桩底。LÜ等[7]从动荷载的角度对支盘桩进行研究，承载板位置不同决定最大承载力。随着工程实际需求变化，由于支盘桩的抗拔性能显著，在工程中的应用也逐步广泛，部分学者对支盘桩的抗拔特性也作了一定的研究，钱德玲[8]基于三维有限元数值模拟，对支盘桩的受力机理、荷载传递性状和上拔荷载作用下应力场及位移场的变化规律进行研究，得出支盘桩的最佳盘间距、桩间距，为挤扩支盘桩的优化设计提供了重要的量化依据。赵明华等[9]对挤扩灌注桩的桩抗拔承载机理、抗拔破坏形式以及拔承载力计算方法进行理论探究，为抗拔桩设计提供理论依据。肖琦等[10]通过现场试验对支盘的存在对桩身轴力影响规律及其上拔荷载传递规律进行研究，提出承力盘间距的合理值。目前主要是通过现场试验或数值模拟对支盘桩的承载特性、破坏形式研究，进行合理的支盘设计。目前，支盘桩在工程中的应用较广，主要是以提供竖向承载力为主，大量的学者[1−7]对支盘桩的竖向承载特性进行研究，分析支盘桩的单桩竖向承载力特性，从支盘位置、支盘大小、支盘形状、支盘间距以及支盘数量等方面得出使其单桩竖向承载力达到最大时的设计参数。支盘桩除了提高竖向承载力外，对抗拔承载力也有极大的提高，部分学者[8−11]基于支盘桩抗拔承载特性，探讨了支盘大小、形状、间距和数量等参数与单桩极限抗拔承载力之间的关系，但对于支盘抗拔桩的设计中涉及到地表与其最近支盘的距离设计，即首盘深度设计，由于目前对这方面的研究较少，故对其认识不足，导致在抗拔工程上的应用较少，因此对支盘桩进行上拔荷载作用下最优盘距的研究是非常必要的。由于支盘桩现场试验非常困难，造价极高，然而数值模拟可操作性强，计算结果与实际非常接近，故本文主要通过数值模拟的方法，对不同桩长的支盘桩设置不同的首盘位置，探讨出支盘深度对极限抗拔承载力的影响规律，从而确定出最优首盘深度范围，为实际工程提供理论依据。

1 支盘桩有限元模型建立

采用双盘桩和三盘桩作为计算模型[12]，桩的截面取为圆形，直径=0.5 m，桩土模型两侧设置水平向位移约束，底端设置水平向和竖直向位移约束。承力盘形状选择时，由于支盘截面为锥形与矩形2种形状的轴向应力基本相同，其抗拔承载特性也基本一致[13]。为使计算模拟方便，将三盘桩的底盘与次盘以最优盘距固定[1, 3]，如图1所示，对双盘、三盘桩模型进行等效简化。将桩设置在一密实黏土地基中，在不排水条件下对桩的工作性状进行探究。试验模拟支盘桩和桩周土的材料参数见表1[14]。

为提高模拟数据的可靠性，采用不同长度的双盘桩和三盘桩进行数值分析，通过模拟不同首盘深度的支盘桩所对应的极限抗拔承载力，研究首盘深度与桩极限承载力之间的变化规律，采用控制变量的方式进行研究，具体参数见表2和表3。

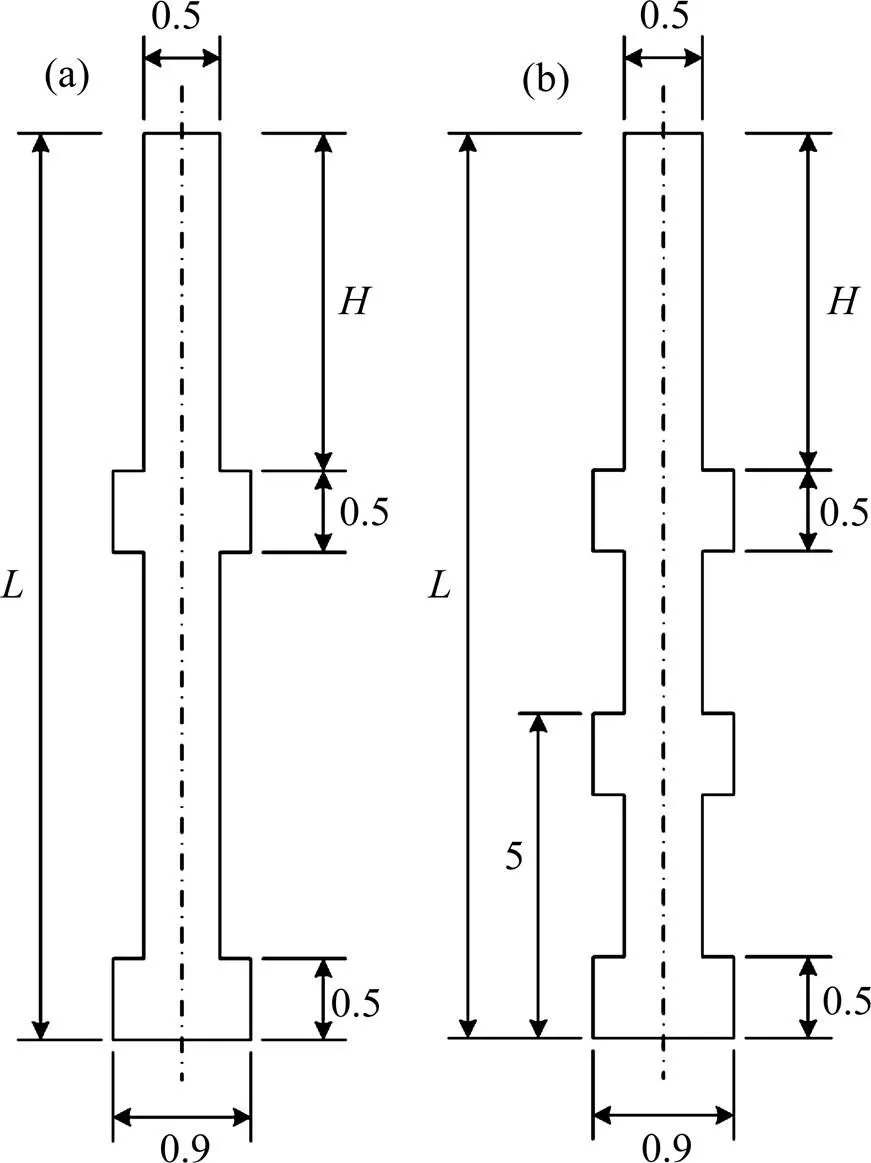
单位：m

表1 材料的物理力学参数

表2 双盘桩模型参数

在数值模拟过程中，将桩考虑为线弹性材料，土体根据实际情况考虑为弹塑性材料，并采用Mohr-Coulomb非线性弹塑性模型模拟土的塑性性质[12]。建立轴对称几何模型。通过设置桩土界面上黏结接触面来模拟桩土之间的相互作用，并对桩和土分别赋予属性参数；通过装配使桩与土形成整体；为了和初始应力相适应，对模型全体施加体力荷载；根据土性参数设置初始地应力场；通过指定桩顶位移，对桩顶施加上拔荷载力；设置模型边界条件，如图2所示。采用轴对称四节点双线性轴对称四边形单元(CAX4)对模型进行网格划分，并对局部集中受力区进行网格加密，如图3所示。

表3 三盘桩模型参数

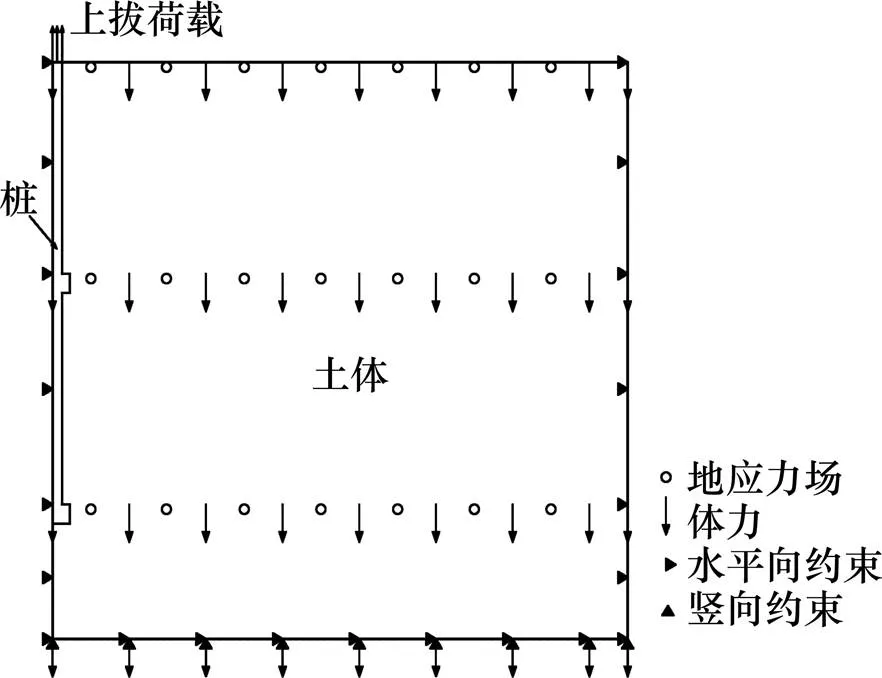
图2 模型荷载及边界条件

图3 模型网格划分结果

2 桩土受力特性

抗拔支盘桩采用钢筋混凝土桩，利用现场钻孔灌注方式成桩，支盘处利用挤扩成型，填入素混凝土。对于桩，数值模拟采用线弹性模型，相比于土体变形，桩的变形可以忽略不计。桩体竖向力分布如图4所示，竖向力沿着桩身呈递增整状态，桩顶的竖向力与位移最大，当桩顶施加上拔荷载的初期，此时在桩身中下部桩土相对位移等于0处，其桩摩阻力因尚未开始发挥作用而等于0，而对于桩周土，第1个盘先受力，随着桩顶上拔荷载增加，桩身混凝土拉伸量和桩土相对位移量逐渐增大，桩侧中下部土层的摩阻力随之逐步发挥出来。支盘处的轴力相比桩身较小，这与桩身的材料刚度和加载过程有关。

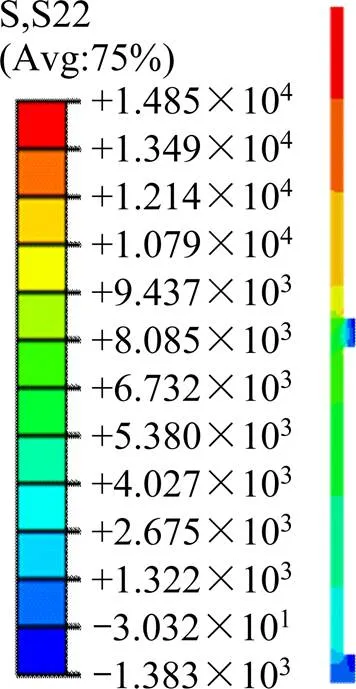
单位：kPa

桩周土体假定为均匀土，指定土体参数模拟实际受力，采用Mohr-coulomb模型模拟不排水黏结强度，内摩擦角取为0，Mohr-coulomb模型退化为Tresca模型[14]，数值模拟分析均匀土的Tresca应力如图5所示。土在支盘处的受力最大，产生的“应力泡”符合土体实际受力情况，主要是桩在受到上拔力作用时，除了桩土侧摩阻力提供抗拔承载力外，支盘所承受的上拔荷载更大程度的分配给周围土体，大大提高了抗拔承载力。

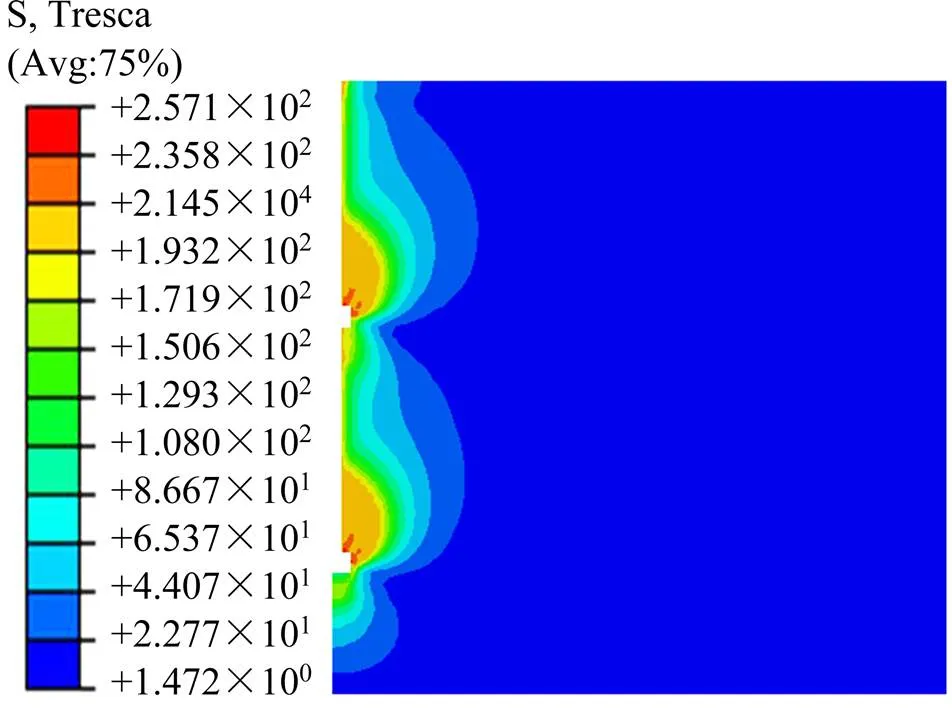
单位：kPa

3 极限抗拔承载力确定

将桩顶节点竖向应力S22的平均值作为桩顶应力代表值，乘以桩身曲线出现明显弯折点所对应的上拔荷载作为极限抗拔荷载，从而确定出不同首盘深度条件下支盘桩的极限抗拔承载力。

4 支盘桩抗拔承载力随首盘深度的变化规律

以双盘桩和三盘桩模型为例，通过分析上拔荷载−位移曲线对不同桩长支盘桩的抗拔承载力进行分析，进一步得出支盘桩的极限抗拔承载力随首盘深度的变化规律，从而确定首盘深度的最优值。

4.1 双盘桩的上拔荷载变化曲线

双盘桩模型主要是通过固定桩底盘，对不同首盘深度支盘桩分别进行承载力模拟，得出不同首盘深度对应的上拔荷载−位移曲线，如图6所示。上拔荷载−位移曲线曲线呈缓慢变化型，上拔荷载随着位移的增大而增大，由线性变化转为非线性，斜率逐渐减小，其-曲线呈缓慢变化型[15]。

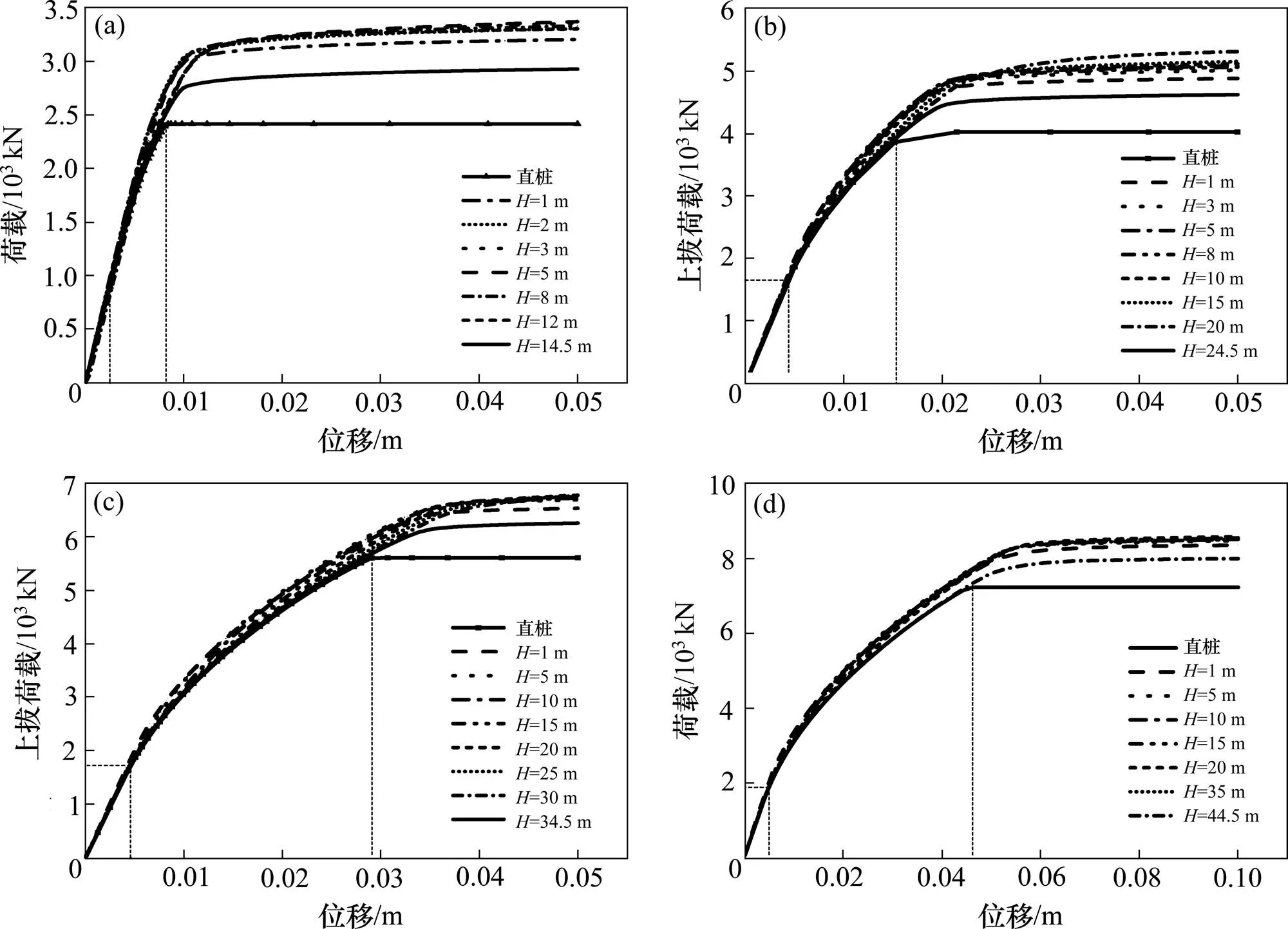
(a) L=15 m；(b) L=25 m；(c) L=35 m；(d) L=45 m

对比图6(a)~6(d)，不同长度支盘桩的桩顶位移在0.005 m范围内，上拔荷载值均随位移呈线性增大，且不同首盘深度对应的上拔荷载位移曲线几乎重合，这是由于此阶段支盘还未受力，承载力由桩侧摩阻力提供。在桩顶位移大于0.005 m时，曲线斜率产生差异，此时首盘深度=1 m的曲线斜率最大，其原因主要是桩在上拔荷载作用下，距地面最近的支盘先受力，从而导致在出现极限抗拔承载力之前的上拔荷载位移曲线，在相同桩顶位移条件下，其上拔荷载值随首盘深度的增大反而减小。对比不同长度的支盘桩，直桩的上拔荷载超过峰值后，上拔荷载位移曲线斜率几乎为零，这是由于直桩主要依靠桩侧摩阻力承受上拔荷载，桩在上拔荷载作用下，使桩土之间的错动位移达到极限位移，产生相对滑动，此时静摩擦力转化为动摩擦力，其值保持不变，最终使得抗拔承载力值保持不变。而对于相同长度的支盘桩，随着首盘深度的增大，峰值后的上拔荷载位移曲线斜率均随首盘深度呈正比例增加。通过对比不同桩长的极限上拔荷载对应的位移值，极限上拔荷载值下的位移值随桩长的增加而增加，验证了桩长是决定桩基承载力的因素之一，与实际规律符合。对于长度一定的桩，在桩底固定一个支盘的单盘桩，其抗拔承载力极限值较直桩有大幅度提高，而双盘桩的极限抗拔承载力较单盘桩的增加幅度有所降低，由于支盘的逆端承作用，盘数的增加必然使得抗拔承载力提高，但其盘数存在合理值使得承载力最大[3]。当桩长超过45 m，无论首盘深度大小，荷载位移曲线较集中，抗拔承载力随首盘深度的影响变化幅度不大，故而桩长对首盘深度的选择有一定的影响，即桩的支盘设计在一定程度上受桩长的限制。

通过对比双盘桩在不同首盘深度条件下的上拔荷载位移曲线，利用各个曲线拐点所对应的极限上拔荷载值，得出与双盘桩极限上拔荷载随首盘深度的变化曲线，如图7所示。

根据双盘桩的首盘深度−上拔荷载曲线图，得出峰值上拔荷载对应得首盘深度值，即使得支盘桩抗拔承载最大时所对应的首盘深度，对比不同桩长的首盘深度−上拔荷载曲线图。对于桩长=15 m的桩，上拔荷载峰值达到3 092 kN，对应首盘深度=4.25 m，占总桩长的28.3%；桩长=25 m的桩，上拔荷载峰值达到4 871 kN，对应首盘深度=6.08 m，占总桩长的24.5%；桩长=35 m的桩，上拔荷载峰值达到6 573 kN，对应首盘深度=8.78 m，占总桩长的25.1%；桩长=45 m的桩，上拔荷载峰值达到8 316 kN，对应首盘深度=10.9 m，占总桩长的24.2%。对比4组相同盘数、不同长度的支盘桩，其上拔荷载峰值对应的首盘深度占桩长的比例，分布范围大致在24%~30%之间，对于桩长45 m的支盘桩，首盘深度对其上拔荷载峰值影响不是太明显，桩的支盘设计在一定程度上受桩长的限制。

试验模拟得出上拔极限荷载值随桩长的变化规律，如图8所示，当桩周土为黏土且处于饱和状态时，直桩的极限抗拔承载力随桩长呈线性增加，桩长每增加单位长度，上拔极限荷载值约增加 160 kN。

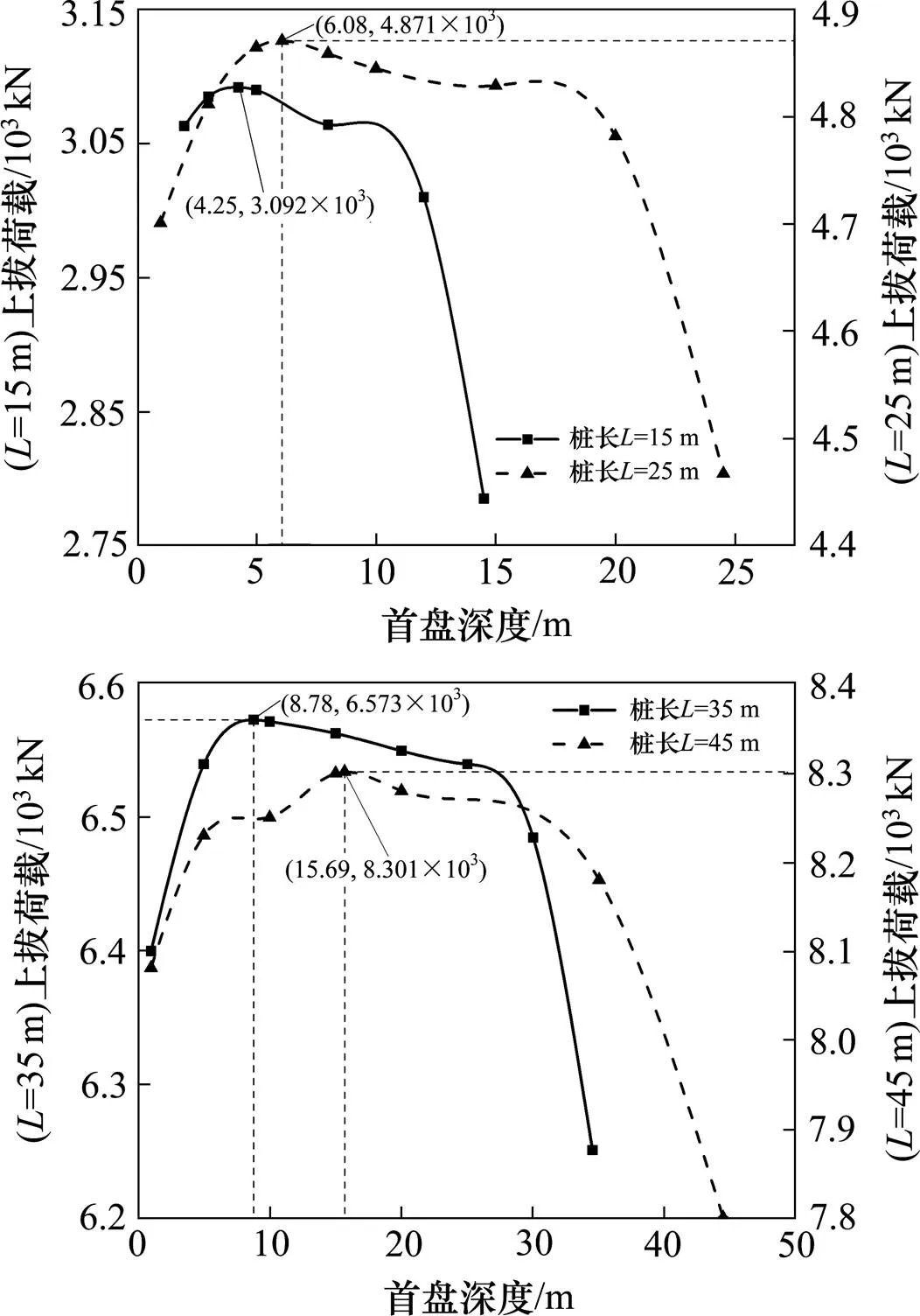
图7 双盘桩的首盘深度−上拔荷载曲线

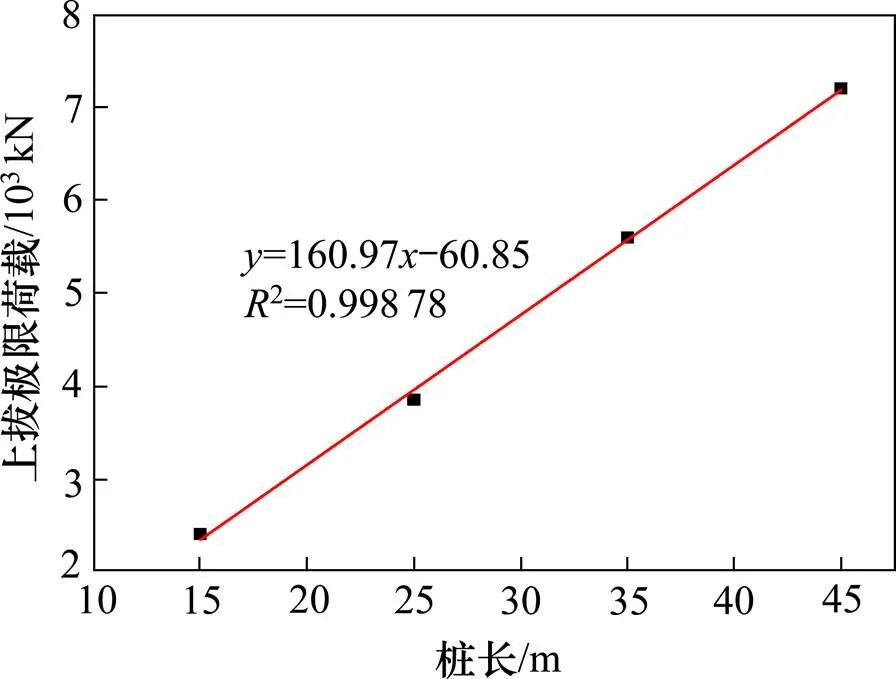
图8 直桩桩长−上拔极限荷载曲线

4.2 三盘桩的上拔荷载变化曲线

三盘桩支盘布置主要以最优间距将底盘与次盘进行固定，对桩长20 m和25 m的支盘桩分别进行不同首盘深度的抗拔承载力模拟，得出不同支盘深度对应的上拔荷载−位移曲线，如图9所示。对于桩长为25 m的支盘桩，直桩在上拔荷载作用下，极限上拔荷载约为3 800 kN，桩底设置一个支盘时，极限上拔荷载约为4 460 kN，利用最优盘距设置两个盘时，极限上拔荷载约为4 900 kN，设置3个盘时，最大极限上拔荷载约为5 225 kN。支盘桩承载力相比直桩有所提高，随着盘数的增加，桩基承载力也随之增加，但增加幅度逐渐较小，故而支盘桩盘数存在一个合理值[3]。与双盘桩类似，桩长对首盘深度的选择有一定的影响，当桩长超过45 m，抗拔承载力随首盘深度的影响变化幅度不大，故而桩的支盘设计在一定程度上受桩长的限制。

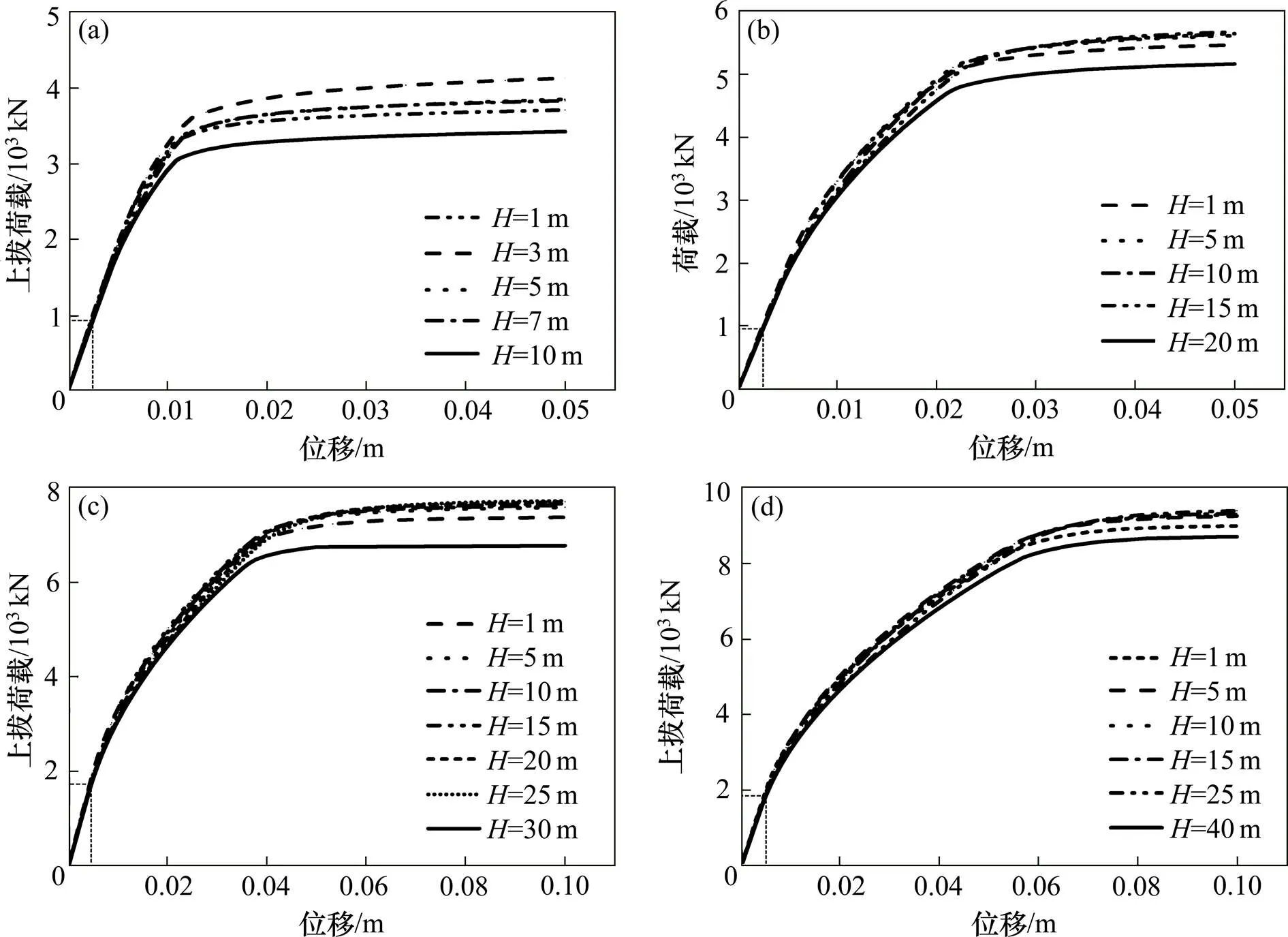
(a) L=15 m；(b) L=25 m；(c) L=35 m；(d) L=45 m

与双盘桩类似，绘制三盘桩的首盘深度−上拔荷载曲线，如图10所示。

根据三盘桩首盘深度−上拔荷载曲线中的峰值坐标，得出上拔荷载峰值对应的首盘深度，即使得支盘桩抗拔承载最大所对应的首盘深度。对于桩长=15 m的桩，次盘深度为10 m，上拔荷载峰值达到3 597 kN，对应首盘深度=3.0 m，占总桩长的20.0%，占次盘深度的30.0%；桩长=25 m的桩，次盘深度为20 m，上拔荷载峰值达到5 220 kN，对应首盘深度=5.81 m，占总桩长的23.2%，占次盘深度的29%；桩长=35 m的桩，次盘深度为30 m，上拔荷载峰值达到7 047 kN，对应首盘深度=8.425 m，占总桩长的24.1%，占次盘深度的28.1%；桩长=45 m的桩，次盘深度为40 m，上拔荷载峰值达到8 736 kN，对应首盘深度=11.438 m，占总桩长的25.4%，占次盘深度的28.6%。与双盘桩类似，对比4组相同盘数、不同长度的三盘桩，其上拔荷载峰值对应的首盘深度占次盘深度的比例，分布范围大致在28%~30%之间。根据支盘桩的抗拔破坏形式，破坏过程中将底盘与次盘视为整体，则相对与首盘位置而言，等效桩长便是次盘深度。

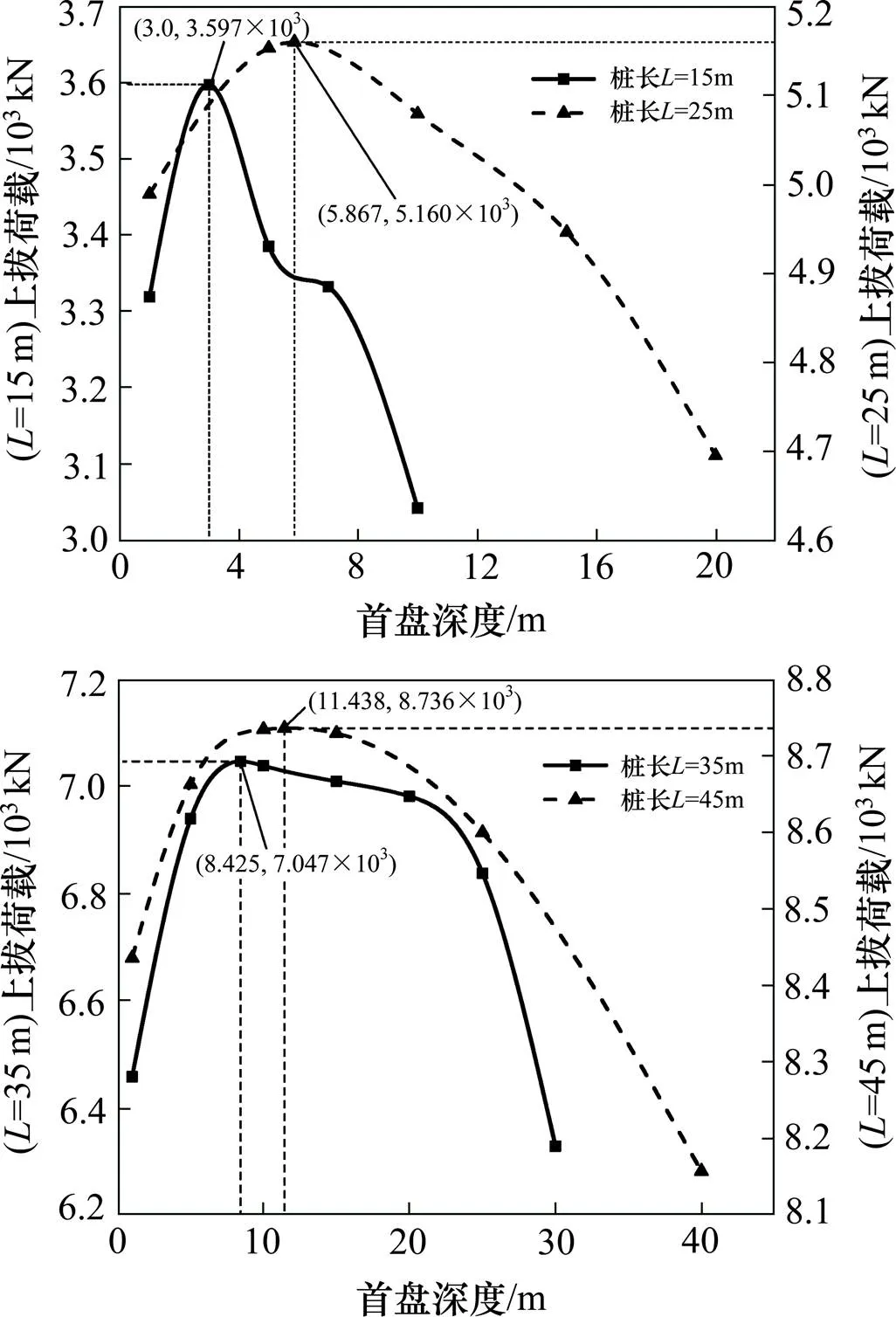
图10 三盘桩的首盘深度−上拔荷载曲线

4.3 对比分析

通过研究双盘桩与三盘桩的抗拔承载力变化规律，对比发现：相比直桩，单盘桩抗拔承载力提高了10%，双盘桩抗拔承载力提高了15%，三盘桩抗拔承载力提高值达到20%以上。主要是支盘的端承作用能有效改善支盘桩的承载性能，充分发挥地基土的承载力，在一定支盘数量下，以及合理的盘距与首盘位置，使得支盘桩相比直桩，抗拔承载力提高将近30%。对于长度不同的支盘桩，首盘深度值为桩长(双盘桩为总桩长、三盘桩为次盘深度)的24%~30%时，对于双盘桩与三盘桩，其抗拔承载力达到最大不同首盘深度条件下，随着桩顶位移的逐步增加，在未达到极限上拔荷载值之前，支盘桩抗拔承载力随着首盘深度的增大而减小，在超过极限上拔荷载之后，其抗拔承载力随着首盘深度增加而增大。

对比双盘桩和三盘桩极限上拔荷载随桩长的变化曲线，如图11所示，在最优首盘深度的条件下，其曲线呈线性变化，且双盘桩与三盘桩对应的曲线近乎平行，双盘桩与三盘桩上拔极限承载力均随着桩长的增加呈线性增长，每单位桩长提供最大抗拔承载力均为172 kN左右。图8与图11对比得出，无论支盘数目多少，当桩周土为黏土且处于饱和状态，支盘桩的单位桩长所提供的抗拔承载力，相比于直桩提高了7.5%。

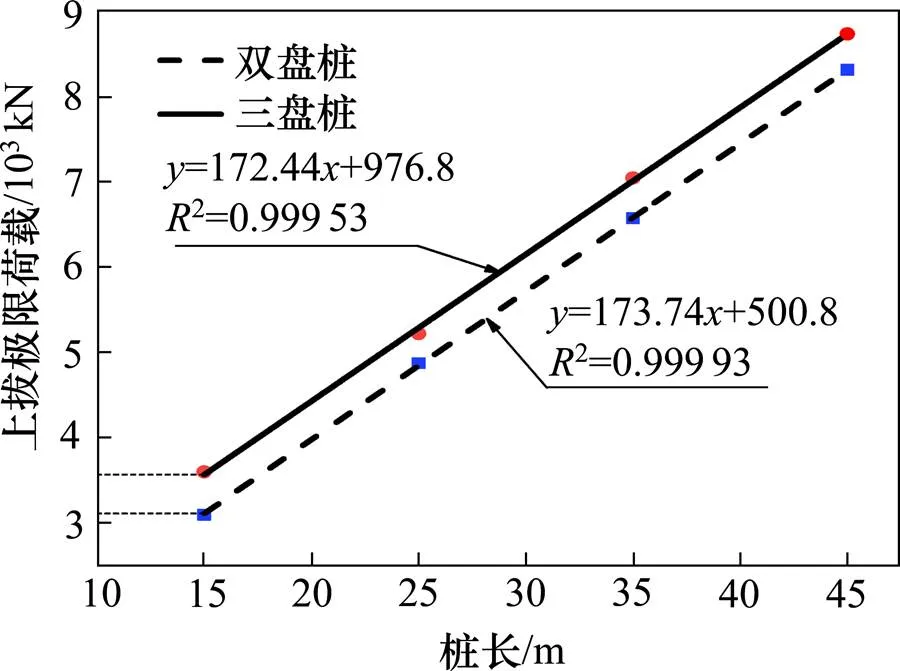
图11 支盘桩桩长−上拔极限荷载曲线

5 结论

1) 相比直桩，单盘桩抗拔承载力提高了10%，双盘桩抗拔承载力提高了15%，三盘桩抗拔承载力提高值达到20%以上。支盘的端承作用能有效改善支盘桩的承载性能，充分发挥地基土的承载力，在一定支盘数量下，以及合理的盘距与首盘深度，使得支盘桩相比直桩，抗拔承载力提高将近30%。

2) 桩长超过45 m时，抗拔承载力随首盘深度的影响变化幅度不大，故而桩的支盘设计在一定程度上受桩长的限制。

3) 对于双盘桩，最优首盘深度占总桩长的比例范围大致分布在24%~30%之间。对于三盘桩，最优首盘深度占“等效桩长”(次盘深度)的比例范围大致也在24%~30%之间。

4) 不同首盘深度条件下，随着桩顶位移的逐步增加，在未达到极限上拔荷载值之前，支盘桩抗拔承载力随着首盘深度的增大而减小，在超过极限上拔荷载之后，其抗拔承载力随着首盘深度增加而 增大。

5)在最优首盘深度的条件下，无论支盘数目多少，当桩周土为黏土且处于饱和状态，支盘桩的单位桩长所提供的抗拔承载力，相比于直桩提高了7.5%，为实际工程中支盘桩的长度设计提供理论支撑。

[1] 范孟华. 基于最小抗力的支盘桩承载力和临界盘间距[J]. 岩土工程学报, 2011, 33(2): 295−298. FAN Menghua. Bearing capacity and critical plate spacing of piles with expanded branches and plates based on the minimum resistance[J]. Chinese Journal of Geotechnical Engineering, 2011, 33(2): 295−298.

[2] 夏红兵, 苏晴晴. 支盘间距、数量、直径对新型支盘桩承载力的影响[J]. 安徽建筑大学学报, 2018, 26(4): 17−21.XIA Hongbing, SU Qingqing. Influence of the new support plate pile bearing capacity on different spacing, numbers and diameter of branches[J]. Journal of Anhui Jianzhu University, 2018, 26(4): 17−21.

[3] 陆凤池, 安里千, 黄业胜, 等. 旋扩珠盘桩的盘间距及其受力分析[J]. 岩土工程学报, 2005(3): 360−364. LU Fengchi, AN Liqian, HUANG Yesheng, et al. Analysis for the distance of two branches and mechanics of the rotated branches pile[J]. Chinese Journal of Geotechnical Engineering, 2005(3): 360−364.

[4] 卢成原, 黄瑜明. 不同土质中支盘桩基础合理盘距和桩距研究[J]. 浙江工业大学学报, 2015, 43(2): 232− 236.LU Chengyuan, HUANG Yuming. Research on the reasonable plates pacing and piles pacing of branch pile foundation indifferent soils[J]. Journal of Zhejiang University of Technology, 2015, 43(2): 232−236.

[5] 卢成原, 寿亚锋, 琚蕊雄, 等. 不同形状盘体组合对支盘桩承载性状影响研究[J]. 浙江工业大学学报, 2017, 45(4): 467−472. LU Chengyuan, SHOU Yafeng, JU Ruixiong, et al. Research on the bearing capacity of branch piles with different plate combinations[J]. Journal of Zhejiang University of Technology, 2017, 45(4): 467−472.

[6] KE J, ZHANG K, ZHOU Z. Study on bearing characteristics of pile with branch plate[J]. Building Science, 2007(5): 28−30.

[7] LÜ B, GAO X J. Model test study of squeezed branch pile under horizontal vibration load[C]// Applied Mechanics and Materials. Trans Tech Publications, 2014, 580: 109−112.

[8] 钱德玲. 利用数值仿真系统实现支盘桩的上拔荷载传递性状[J]. 土木工程学报, 2004, 37(4): 68−72.QIAN Deling. To actualize transferring behavior of load in squeezed branch pile by numeral emulation system[J]. China Civil Engineering Journal, 2004, 37(4): 68−72.

[9] 赵明华, 李微哲, 单远铭. DX桩抗拔承载机理及设计计算方法研究[J]. 岩土力学, 2006(2): 199−203. ZHAO Minghua, LI Weizhe, SHAN Yuanming. Study on uplift mechanism and calculation of DX pile[J]. Rock and Soil Mechanics, 2006(2): 199−203.

[10] 肖琦, 王德弘, 徐晶. 输电线路挤扩支盘桩受力特性的试验研究[J]. 实验力学, 2015, 30(1): 124−130. XIAO Qi, WANG Dehong, XU Jing. Experimental study of squeezed branch pile mechanical characteristics in transmission line engineering[J]. Journal of Experimental mechanics, 2015, 30(1): 124−130.

[11] TANG L, LU C. Research progress on the project behavior of pile with plates and branches[J]. Journal- Zhejiang University of Technology, 2006, 34(6): 622.

[12] KE J. Study of working properties of pile with branch plates based on Abaqus[C]// 2011 Second International Conference on Mechanic Automation and Control Engineering. IEEE, 2011: 6868−6871.

[13] 范孟华, 刘国涛, 孔德志. 承力盘对支盘桩单桩负摩阻力影响的有限元分析[J]. 河南大学学报(自然科学版), 2015, 45(4): 499−504. FAN Menghua. LIU Guotao, KONG Dezhi. Bearing plates influence of negative friction of single pile withplates via finite element analysis[J]. Journal of Henan University (Natural Science), 2015, 45(4): 499− 504.

[14] 费康, 张建伟. ABAQUS在岩土工程中的应用[M]. 北京: 中国水利水电出版社, 2010. FEI Kang, ZHANG Jianwei. Application of ABAQUS in geotechnical engineering[M]. Beijing: China Water Conservancy and Hydropower Press, 2010.

[15] JIA J L, WANG Z F, ZHENG J H. Experimental study on bearing behavior of large-diameter over length squeezed branch pile[C]// Advanced Materials Research. Trans Tech Publications, 2011, 243: 3244−3250.

A study on the relationship between first disk depth and pullout resistance of uplift branch pile

YANG Zhijun, XIE Yongli, FAN Xiang, LU Yixin

(School of Highway, Chang’an University, Xi’an 710064, China)

The determination of the first plate depth has great practical significance in the actual engineering, with the extensive application of the anti-drawing branch pile in the engineering field. Based on the numerical calculation theories of elastoplastic constitutive relation of rock and soil, ABAQUS finite element software was used to establish the model of pile and soil axis symmetry. Considering the initial stress field, the model of pile-soil interface bonding was defined. Under the condition of specified displacement of pile top, the variation of uplift bearing capacity of the pile support pile was analyzed, and the influence of the first plate depth on the uplift capacity of the pile support pile was obtained. The comparative analysis of the up-and-down load-displacement curves of different pile lengths shows that: With the increase of displacement which occur on pile top for the branched piles with different depths of first plate, the uplift bearing capacity decreases with the increase of the first plate depth before the ultimate uplift load is reached, and when the ultimate uplift load is reached, the uplift bearing capacity increases with the increase of the first plate depth; For the branch piles with different lengths, the first plate depth value is 24%~30% of the pile length (the double plates pile is the total pile length and the three plates pile is the secondary depth), and the uplift bearing capacity reaches the maximum; Under the optimal first plate depth, regardless of the number of branch plates, when the soil around the pile is clay and saturated, the uplift bearing capacity provided by the unit pile length of the branch-plate pile is 7.5% higher than that of the straight pile. It provides theoretical support for the length design of branch-plate pile in practical engineering.

finite element analysis; branch pile; uplift bearing capacity; depth of first plate; uplift load- displacement curve

TU473

A

1672 − 7029(2019)10− 2442 − 09

10.19713/j.cnki.43−1423/u.2019.10.009

2018−11−25

国家自然科学基金资助项目(41807241)；浙江省交通运输厅科研计划项目(2019043)

谢永利(1961−)，男，山西芮城人，教授，博士，从事公路岩土与隧道工程研究；E−mail：xieyl@263.net

(编辑 涂鹏)