轻量化造船中薄板对接焊失稳及其临界条件

易 斌，史雄华，殷咸青，周方明，王江超*

(1.华中科技大学 船舶与海洋工程学院，湖北 武汉 430074；2.西安交通大学 金属材料强度国家重点实验室，陕西 西安 710049；3.江苏科技大学 先进焊接技术省级重点实验室，江苏 镇江 212003)

0 引 言

为了节约能源、保护环境，大型结构轻量化是当今时代制造业发展的主题。因此，高强钢薄板越来越多地被应用于船舶、汽车和航空航天等领域。特别是对于现代化造船来说，薄板焊接结构不仅满足船舶营运的经济性要求，同时也能完全满足船舶行驶的强度和刚度。但是，薄板因其厚度的减小稳定性显著降低，在焊接制造过程中易产生失稳变形现象，这给薄板焊接结构的装配精度带来很大的负面影响[1]。因此，对于薄板焊接失稳变形的研究具有十分重要的工程应用价值。

焊接失稳变形是薄板焊接结构中比较复杂的现象，具有多种不同的面外变形模式[2]。因此，对于薄板焊接失稳变形的预测具有一定的难度。王晓光等[3]利用XJTUDIC三维数字散斑动态应变测量分析系统对薄板的焊接变形进行动态跟踪测量得到整个试件全场的焊接变形。倪连超等[4]利用有限元软件ABAQUS，采用顺序耦合的热-弹-塑性有限元法研究EH36钢薄板焊接变形问题，并研究网格精度对计算结果的影响，指出焊缝区网格细化的程度对计算结果影响不大。MICHALERIS等[5]同样利用ABAQUS软件，使用基于大变形理论的三维热-弹-塑性有限元方法，分析T型焊接接头的失稳现象，计算结果与试验测量结果具有很好的一致性，但计算时间较长。WANG等[6]使用非耦合的热-弹-塑性有限元计算程序(JWRIAN)研究薄板堆焊产生的焊接失稳变形，计算结果与试验结果具有相同的模态，且面外变形与试验结果基本吻合。

基于大量试验和对热-弹-塑性有限元计算结果的分析，认为焊接过程中的残余塑性应变是焊接变形和残余应力的生成源，也就是固有应变[7]。为提高计算效率，节约计算时间，基于固有应变的弹性有限元分析被广泛应用于大型焊接结构件的数值模拟计算中。DENG等[8]使用非耦合的热-弹-塑性有限元分析与基于固有变形的弹性有限元分析相结合的方法分析大型焊接结构的焊接变形。弹性有限元分析实际焊接结构的面外变形时，使用到界面单元和典型接头的固有变形。WANG等[9-10]将上述复合方法进行完善，对热-弹-塑性有限元分析得到的典型焊接接头的固有应变进行积分求和，得到更加精确的固有变形数值，很好地预测船体板架结构和自升式平台悬臂梁的焊接变形，并提出控制焊接变形的措施。当前，随着数字图像相关技术的发展，已经存在能够实时测量整个焊接过程的仪器。

本文首先进行薄板对接焊试验，然后基于大变形理论和固有变形理论，分别使用热-弹-塑性有限元分析和弹性有限元分析来研究薄板对接接头(尺寸为300 mm×200 mm×3 mm)的焊接变形。将热-弹-塑性有限元分析和弹性有限元分析这两种方法得到的数值模拟结果与试验结果进行对比，并计算得到薄板对接接头产生失稳变形的临界条件。

1 有限元分析及理论

1.1 热-弹-塑性有限元分析

完整的焊接热-弹-塑性有限元分析包括瞬态热分析和力学分析等2个过程。瞬态热分析对力学分析结果有决定性的作用，力学分析结果对瞬态热分析结果影响较小。因此，本文主要采用非耦合的热-弹-塑性有限元方法分析薄板对接接头的焊接变形，主要包括以下2个步骤：

(1)使用热力学理论(热传导和热对流)计算得到整个薄板对接接头的瞬态温度场。

(2)将热分析计算得到的瞬态温度场作为有效热载荷施加到随后的力学分析过程中，计算得到薄板对接接头塑性应变、残余应力和焊接变形等。

在计算中，环境温度设置为初始温度(20 ℃)，焊接电弧热源假设为热流密度均匀的体热源，且考虑热对流和热辐射引起的热损失。在焊接加热时，根据总的焊接时间来定义计算时间步长以保证计算精度和计算效率；在焊接结束后，时间步长呈指数增加直至冷却至初始温度(20 ℃)，进而提高计算效率。

1.2 弹性有限元分析

弹性有限元分析主要是基于固有变形(焊接变形和残余应力产生的根源)的理论。焊缝在加热过程中会膨胀，由于周围母材的约束会受到压应力，当压应力大于材料的屈服极限时产生压缩塑性应变。冷却过程则正好相反，焊缝在拉伸应力作用下会产生拉伸塑性应变，抵消部分加热过程中产生的压缩塑性应变，而剩余的压缩塑性应变则被保留下来产生焊接变形和残余应力，也就是固有应变。压缩塑性应变作为主要的固有应变分量，其数值主要取决于焊材性能、焊接接头类型、焊接热输入和板厚等参数，而焊接接头的长度和宽度(足够长和足够宽)的影响可忽略不计。

为了解决实际工程应用中固有变形加载不便的问题，将垂直于焊缝方向的固有应变进行积分，得到4个固有变形分量，再加载进行弹性有限元分析，这是一种简便且行之有效的方法。

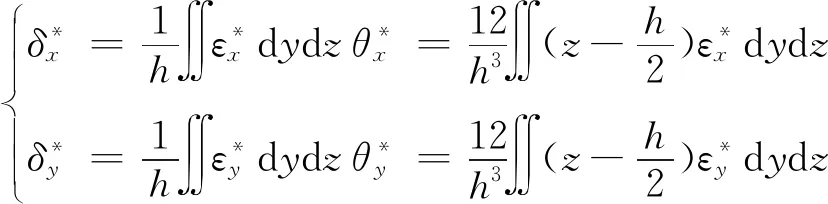
(1)

式中：ε为固有应变；δ为固有变形；θ为固有弯曲；x、y、z分别表示沿焊缝方向、垂直于焊缝方向和沿板厚度方向；h为焊缝的厚度。

1.3 大变形理论

描述焊接失稳变形现象需要考虑位移与应变的关系。如果焊接变形很小，则应变与位移之间通过线性关系表征即小变形理论；当焊接变形比较大的时候，应变则需要通过位移的非线性函数关系表征，即格林-拉格朗日应变方程。从该位移-应变关系可以看出：一阶项表示的是线性响应，二阶项表示的是高阶响应，且非线性项对大变形理论是必不可少的。

2 焊接试验及测量

在试验过程中，利用三维数字散斑动态应变测量分析系统对薄板(材料Q235钢，尺寸为300 mm×200 mm×3 mm)的TIG焊接面外变形进行动态跟踪拍摄，并改变薄板焊接的电流、电压等焊接参数，测量得到不同焊接热输入下的焊接变形。其中，试件被放置在工作平台上，为了避免焊接弧光对测量过程的影响，焊接过程在试件上方进行，测量过程在试件下方开展。图1所示为试验装置。

图1 试验装置

试验分别对3组不同热输入下的薄板对接焊变形进行试验测量，具体焊接参数如表1所示，单位长度热输入计算式为式(2)。在试验过程中，选取试件上2条直线测量最后的焊接面外变形，其中沿焊缝方向为线1，垂直于焊缝方向为线2，如图2所示。～点是面外变形比较大的部位，下文会对比相对面外变形得到失稳变形的临界条件。薄板对接焊产生的面外变形试验测量结果如图3所示。

表1 3种焊接参数具体情况

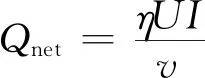
(2)

式中：Qnet为单位长度热输入，简称热输入，J/mm；U为焊接电压，V；I为焊接电流，A；η为热效率；v为焊接速度，mm/s。

图2 焊件几何模型示例

3 薄板焊接过程的有限元计算

热-弹-塑性有限元分析被广泛地应用于焊接变形的预测研究中。下面介绍热-弹-塑性有限元分析的薄板失稳焊接变形预测以及计算结果的分析。

3.1 有限元模型及其网格

热-弹-塑性有限元分析的有限元模型与试件尺寸(300 mm×200 mm×3 mm)完全相同，采用三维实体单元(SOLID)进行网格划分。焊缝处网格应尽量细化，而远离焊缝处网格逐步平稳过渡到相对稀疏。整个薄板有限元模型以及焊缝局部网格划分如图4所示。整个有限元模型单元数为5 950个、节点数为8 058个，沿焊缝方向每个单元长度为6.0 mm。

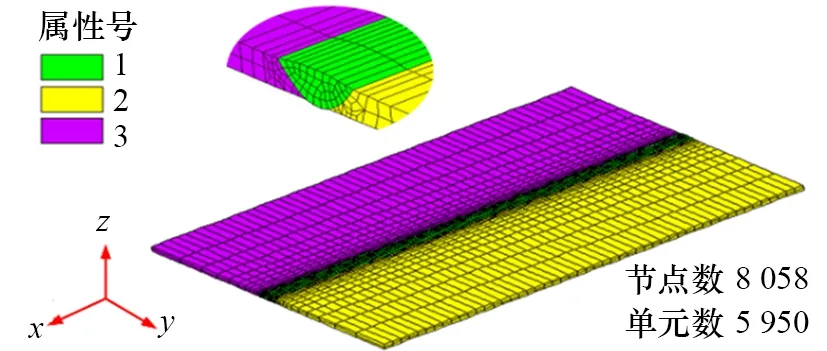
图4 热-弹-塑性分析有限元模型

3.2 计算结果分析

采用非耦合的热-弹-塑性有限元分析，先进行热分析得到温度场，接着将温度场计算结果作为热载荷加载到随后的应力分析中，得到整个薄板的面外变形。热分析时采用与试验完全一致的焊接参数。图5所示为焊接过程中电弧大约经过薄板中心时的瞬态温度场分布云图，温度场分布呈现出椭圆形。应力场的计算完全依赖于温度场的计算结果，基于小/大变形理论计算得到试验中3种焊接参数下薄板的焊接变形。取不同热输入下2条直线上面外变形的计算结果，与试验结果进行对比，如图6所示。

图5 瞬态温度场分布(电弧经过薄板中心处)

图6 热-弹-塑性分析薄板面外变形计算结果与试验结果对比

由图6面外变形结果对比可以看出：小变形理论计算的面外变形结果都很小，与试验结果差别很大；大变形理论计算的结果与试验结果在2个方向上都基本吻合。这是由于当薄板焊接发生失稳变形时，非线性项对计算结果影响很大，起到了决定性的作用。同时，图7给出了热输入为408.0 J/mm时整个薄板面外变形结果云图，最后薄板呈现出“马鞍形”(沿焊缝方向上凸，垂直于焊缝方向下凹)，这是薄板焊接失稳变形的典型特征。

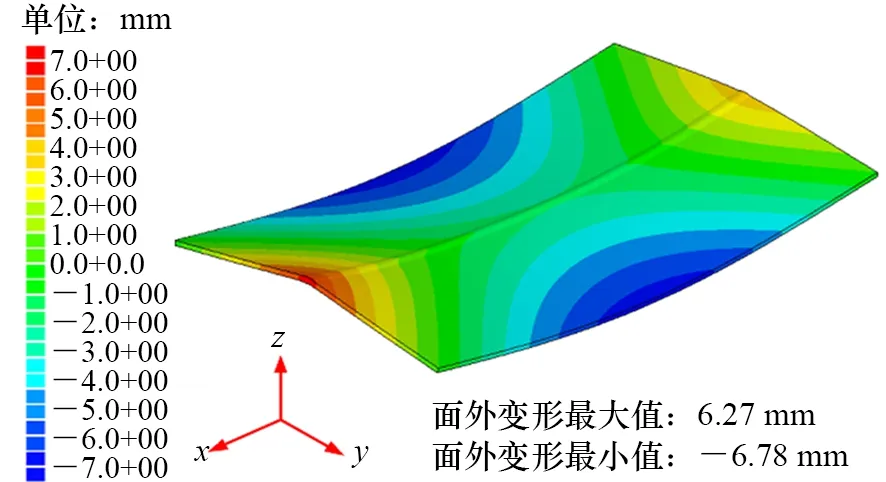
图7 热输入为408.0 J/mm时热-弹-塑性分析面外变形云图

3.3 薄板对接接头失稳的临界条件

在相同的热输入条件下，薄板对接接头面外变形较大，且面外变形不仅包括弯曲角变形还有失稳变形。当热输入减小时，焊接产生的面外变形会变小。因此，为了得到薄板对接接头发生失稳变形的临界条件，在考虑试验已有3组热输入的情况下，增加2组热输入进行热-弹-塑性有限元分析，且仅考虑大变形理论，得到相应的计算结果，具体焊接参数情况如表2所示。取不同热输入条件下1～4点(如图2所示)面外变形数值以及整个薄板面外变形的最大值与最小值，结果如表3所示。经数据分析可以发现：点1、点2与点3、点4的面外变形数值正负号正好相反，这正是“马鞍形”失稳变形的特征。

表2 增加的2组热输入具体焊接参数

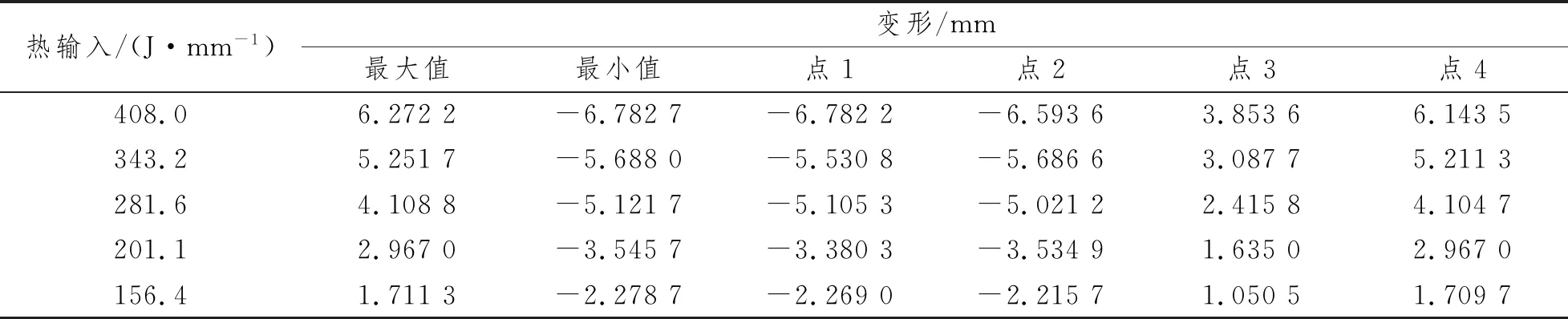
表3 不同热输入时对应的面外变形结果

为了进一步研究薄板对接接头发生失稳变形的临界条件，工程上可将相对面外变形数值进行数据分析，得到5种不同热输入条件下相对面外变形的4次方参数，如图8所示。从图8曲线形状可以观察到：随着热输入的增大曲线斜率迅速增大；当热输入到达一定值后曲线的斜率趋于稳定。存在1条直线(见图8)与曲线斜率稳定区域基本重合，并得到其与横轴的交点横坐标286.87 J/mm即为热-弹-塑性有限元分析的临界条件，可用来指导实际生产，并预防焊接失稳变形的发生。

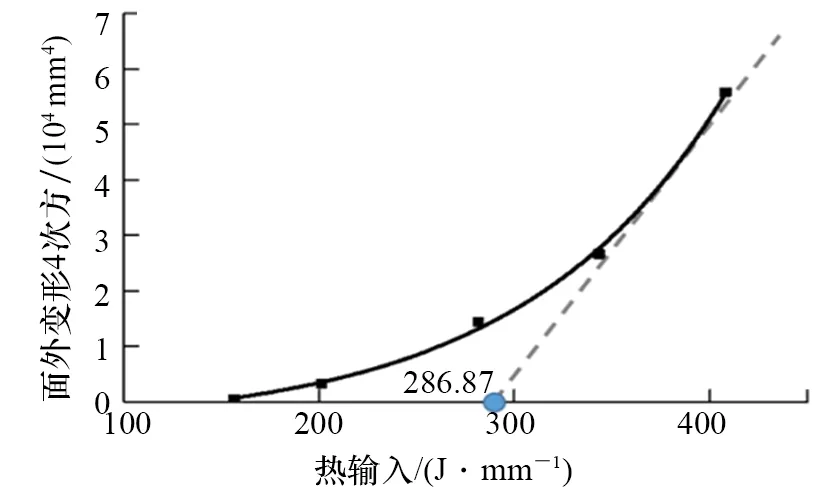
图8 热-弹-塑性分析薄板焊接失稳的临界条件

4 焊接失稳的弹性有限元分析

热-弹-塑性有限元分析能较为准确地预测出薄板的焊接失稳变形，然而其有限元模型复杂，占用大量的计算机资源，且计算时间较长。在弹性有限元分析中，有限元模型相对简单，计算效率高，是一种更加简便的数值模拟方法。

4.1 有限元模型及其网格

使用大尺寸壳单元(SHELL)对焊接接头(尺寸为300 mm×200 mm×3 mm)进行网格划分。应用基于固有变形的弹性有限元分析，节约计算机资源，缩短计算时间。图9所示为薄板对接接头弹性有限元分析的模型，一共有867个节点和800个单元。为了与热-弹-塑性有限元分析的计算结果进行对比，弹性分析有限元模型沿焊缝方向以及垂直焊缝方向(除焊缝处区域)的节点位置与热-弹-塑性分析有限元模型相同。

图9 弹性分析有限元模型

4.2 薄板对接接头固有变形

弹性有限元分析结果准确与否，关键是焊接固有变形的精度。根据热-弹-塑性有限元计算的结果，将得到的每个横断面上的残余压缩塑形应变进行积分得到固有变形的4个分量，包括横向、纵向的面内收缩变形以及面外弯曲变形。忽略焊接引弧和熄弧的影响，取沿着焊缝方向且电弧稳定区域的焊接固有变形作为计算输入参数。基于大变形理论的热-弹-塑性有限元分析结果，不同焊接热输入对应的固有变形数值如表4所示。

表4 不同热输入条件下固有变形数值

4.3 弹性有限元的结果分析

将表4所示的固有变形加载到弹性有限元分析模型中，并基于大变形理论，得到薄板对接接头面外变形的计算结果。图10所示为3种热输入条件下，试验结果、基于大变形理论的热-弹-塑性有限元分析和弹性有限元分析计算结果，分别沿焊缝方向(线1)以及垂直于焊缝方向(线2)的面外变形对比。通过图10中3种热输入下面外变形的对比可以观察到：弹性有限元分析结果与试验结果以及热-弹-塑性有限元分析结果有着很好的一致性，即弹性有限元分析也很好地再现了薄板对接接头焊后的失稳现象。

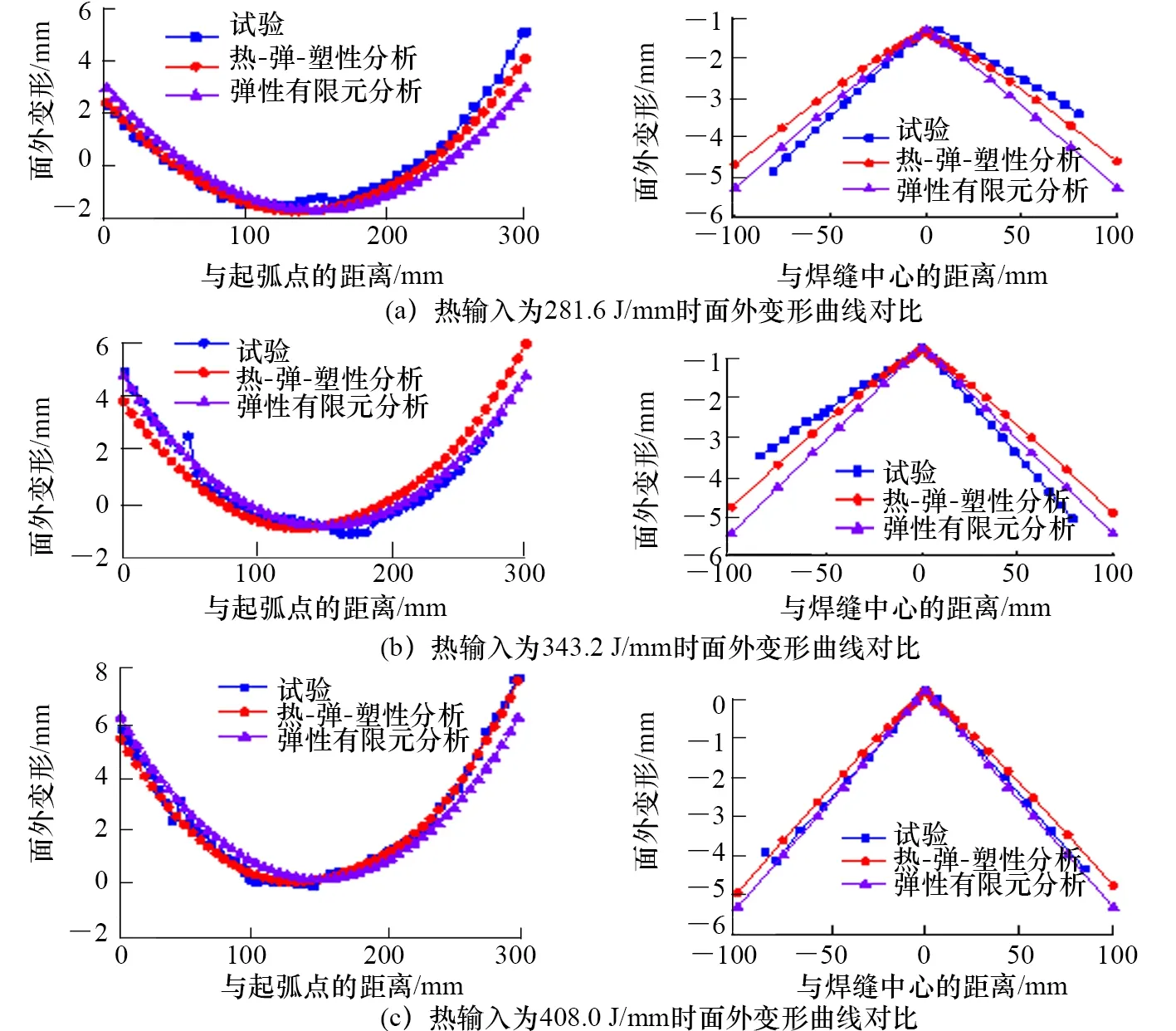
图10 不同热输入下薄板面外变形计算结果与试验结果对比

同时，图11给出了热输入为408.0 J/mm的弹性有限元计算的面外变形云图。与图7相比，薄板对接接头最后都是呈现出相似的“马鞍形”，但两者面外变形方向恰好相反。这是因为当焊接引起的收缩力[6,11]压缩薄板对接接头使其发生失稳变形时，其不稳定性导致可能产生向上或者向下的弯曲变形，并最终呈现出不同方向的“马鞍形”失稳变形。

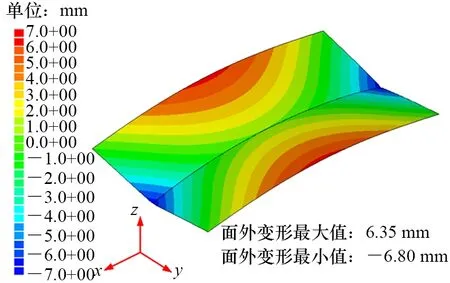
图11 热输入为408.0 J/mm时弹性有限元分析面外变形云图

4.4 薄板对接接头失稳的临界条件

通过弹性有限元分析获得薄板对接接头失稳变形的临界条件，可采用固有变形增量法，逐步加载固有变形，直到薄板对接接头发生大量级的面外变形。具体地，取每一步点1和点4的面外变形数值，得到相对面外变形，并经过4次方运算处理。相对面外变形的4次方参数与加载的固有变形关系如图12所示。

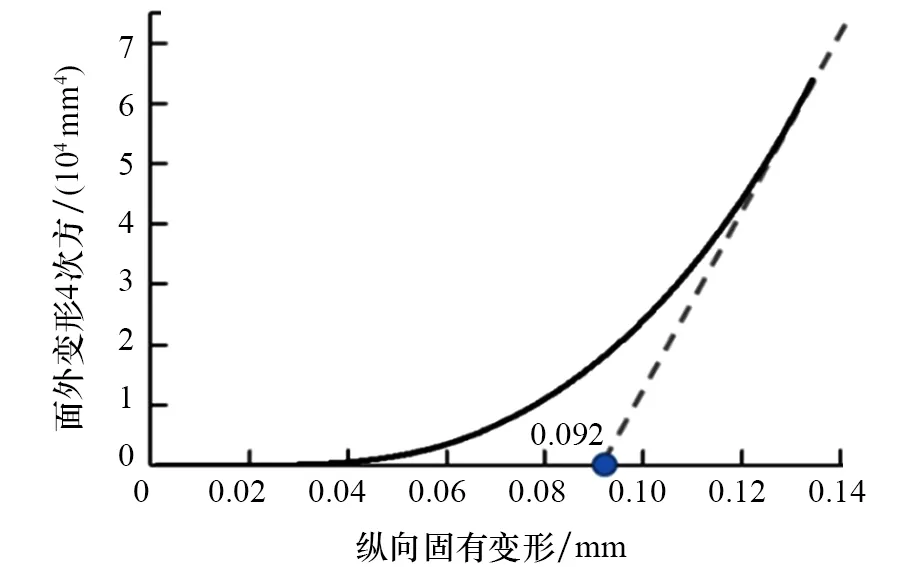
图12 弹性有限元分析薄板焊接失稳的临界条件

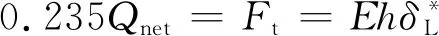
(3)

将热-弹-塑性有限元分析与弹性有限元分析的计算结果进行对比，如表5所示。两种方法计算的结果都与测量数据相当吻合，且基于固有变形的弹性有限元分析具有更加高效，消耗较小计算机资源的优势。

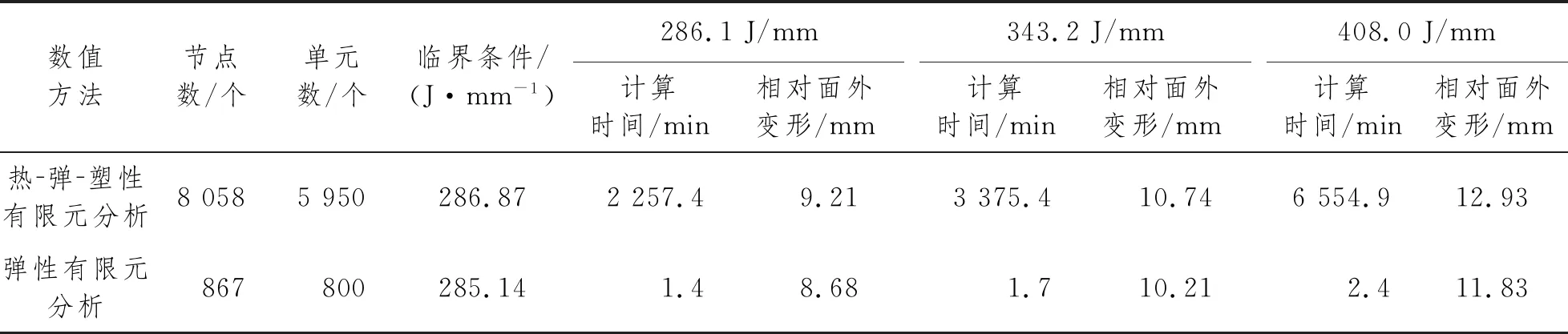
表5 不同热输入下热-弹-塑性与弹性分析结果对比

5 结 论

本文通过试验测量、热-弹-塑性有限元分析和弹性有限元分析等，研究薄板对接接头的焊接失稳变形，并研究该结构产生焊接失稳变形的临界条件。具体结论如下：

(1)薄板对接接头易产生失稳变形，且呈现“马鞍形”。基于大变形的热-弹-塑性有限元分析能够很好地再现失稳变形现象，且预测结果与测量数据相当吻合。

(2)基于精确的焊接固有变形，弹性有限元分析结果与试验测量数据以及热-弹-塑性有限元分析结果都具有很好的一致性。

(3)弹性有限元分析相对于热-弹-塑性有限元分析而言，模型简单，计算机资源需求少，计算效率高。

(4)应用载荷增量法，数值计算可得到薄板对接接头失稳变形产生的临界条件，且两种数值方法计算的临界条件基本一致，对轻量化造船中薄板焊接失稳变形的预防和控制具有重要的工程指导意义。