GPS控制测量在工程测量中的精度分析探讨

魏超 林鲁武 刘丽莉

（1.河南省遥感测绘院，河南 郑州 450003；2.海南思马特测绘规划工程有限公司，海南 琼海 571400；3.偃师市自然资源和规划局，河南 偃师 471900）

1 引言

近年来，GPS 控制测量手段的更新换代，不仅提高了测绘行业的生产技术水平，还全面提升了测绘人员的工作效率[1-2]。GPS 控制测量具有精度高、数据处理智能化等优点，但不可忽视的是，在实际生产运用过程中，GPS 控制测量技术受多种因素干扰影响，精度常常会有所降低，其中一个重要的影响因素就是地形变换引起的转换模型误差[3]，这会导致工程测量结果偏差较大，影响工程建设质量。因而，对GPS 控制测量技术在工程测量中的实际应用进行研究探讨具有重要意义。

2 工程概况

2.1 项目整体概况

项目位于某县级公路Y104-Y133 建设段，路段长约6km，测量区域地形复杂，前4km 地势平坦，后2km地形较为起伏。为满足工程测量需求，已在项目区域布置四等水准测量，以1985 国家高程基准为测量标准，以平面控制网中Z204 作为已知点，由中央子午线102°及GPS 坐标线换算各个平面控制网的边长，进而获得各个测量基点的坐标。

项目采用TCR705 全站仪作为测距仪，精度测量达1.5mm，完成其中每条基准边线的测量工作；将GPS接收信号数据与全站仪测量数据相结合，计算分析后获得各条边长的最大误差为0.0314m，相对误差为1/16250，满足GPS 控制测量精度要求，完成了项目路段GPS 高程转换前期基础工作。

2.2 精度评定标准

采用不同的GPS 高程转换模型，所获得的结果也会有所差异，评价各个模型的优良性需要采用统一精度标准。根据项目测量路段的实际情况，以四等水准测量结果为外符合精度校核[4]，综合内、外符合精度值，综合评定各个转换模型的适用性。

由已知测点与未知测点的高程残差η与拟合转换残差值η＇，获得平面控制网中的内符合精度为：

外符合精度为：

公式中，m、n分别为控制测点与未知测点的个数。

3 模型精度对比分析

3.1 平面区域模型精度对比

在项目前4km 地势平坦段，布设GPS 平面控制网（如图1 所示）。在该区域地段，共设置有7 个控制点，另有7 个待测点，分别对控制点计算残差值及内、外符合精度。

图1 测量区域内GPS平面网

该路段有7 个控制点、7 个未知点，表1、表2 为各测点坐标及高程信息参数。针对平坦地形，项目采用平面拟合法、二次曲面法、平面拟合最小二乘优化、二次曲面最小二乘优化四种模型进行高程转换，依据Matlab 编程得到各个测点拟合结果与高程异常值的残差值，并计算出控制点各个模型的内符合精度与未知点各个模型的外符合精度，如表3、表4 所示。

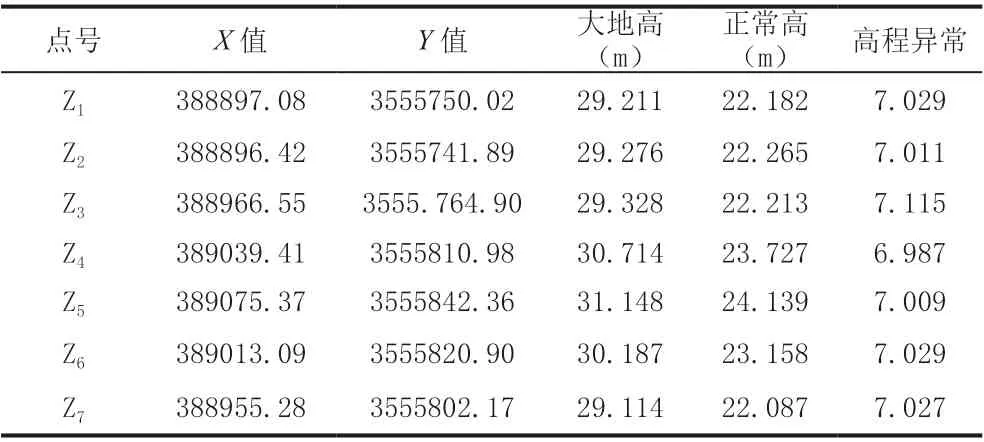
表1 控制点坐标及高程值

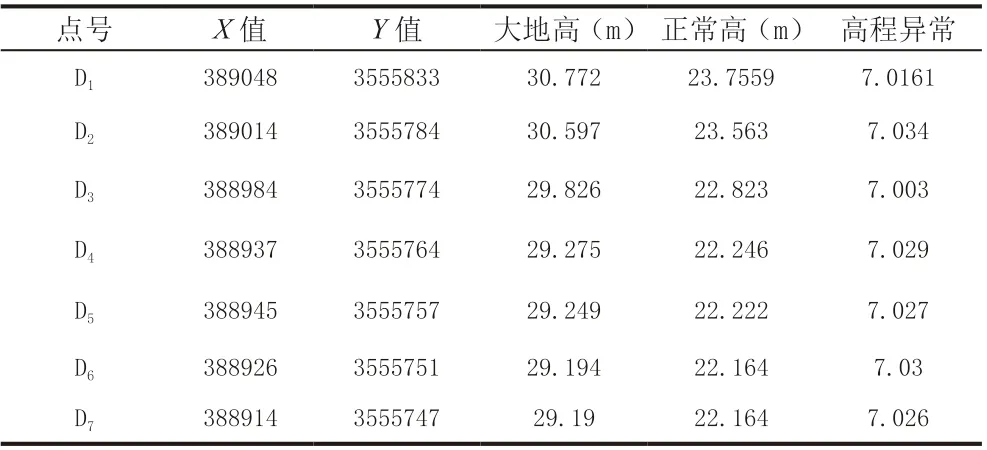
表2 未知点坐标及高程值

表3 控制点高程拟合值及残差值

表4 未知点高程拟合值及残差值

从表3 可以看出，控制点高程拟合结果中，最大残差绝对值最大者是平面拟合法，残差值为-2.3cm ；最大残差绝对值最小者为二次曲面最小二乘优化法，残差值仅为0.8cm；二次曲面法最大残差绝对值为1.9cm；平面拟合最小二乘优化法最大残差绝对值为1.6cm。

从表4 可以看出，未知点高程转换拟合结果中，最大残差绝对值最大者为平面拟合法，残差值达-1.4cm；最大残差绝对值最小者为二次曲面最小二乘优化法，残差值仅为-0.5cm；二次曲面法与平面拟合最小二乘优化法的最大残差绝对值分别为1cm、-1.1cm。

比较各模型的内符合精度可知，控制点结果中，内符合精度最小值为二次曲面最小二乘优化法；未知点结果中，外符合精度最小值亦为二次曲面最小二乘优化法。

综上所述，在平坦路段，采用二次曲面最小二乘优化法精度最高，更具地形匹配性。

3.2 起伏路面模型精度对比

项目区域后2km 为起伏路面，常用的GPS 曲线或曲面转换模型，无法达到理想结果，因而在多项式曲面模型基础上进行模型改进，分别获得了三种多项式曲面改进转换模型，如公式（3）～（5）所示。

改进模型一：

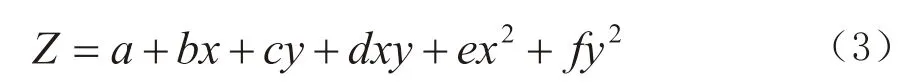
改进模型二：

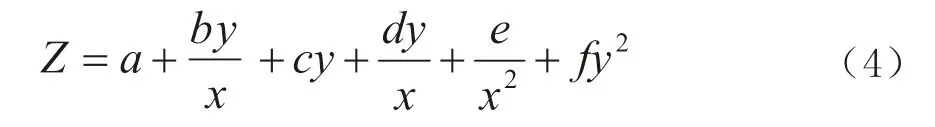
改进模型三：

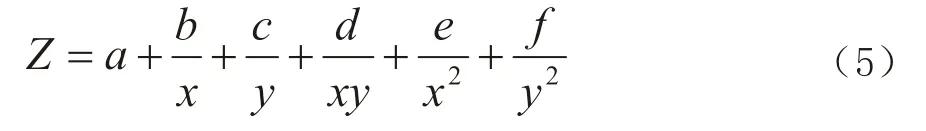
于起伏路段的测点数据，对三种模型进行转换，得到各个测量点的高程异常值，进而计算出各测点的残差值（如表5 所示）。

为了对比不同模型之间的精确度，仅仅对各个模型转换GPS 点的结果计算残差还远远不够，需要依据内、外符合精度来判断控制点高程异常值与未知点高程异常值之间的误差。因而，项目对不同转换模型的高程异常值和内、外符合精度进行了对比，以确定模型的适用性。

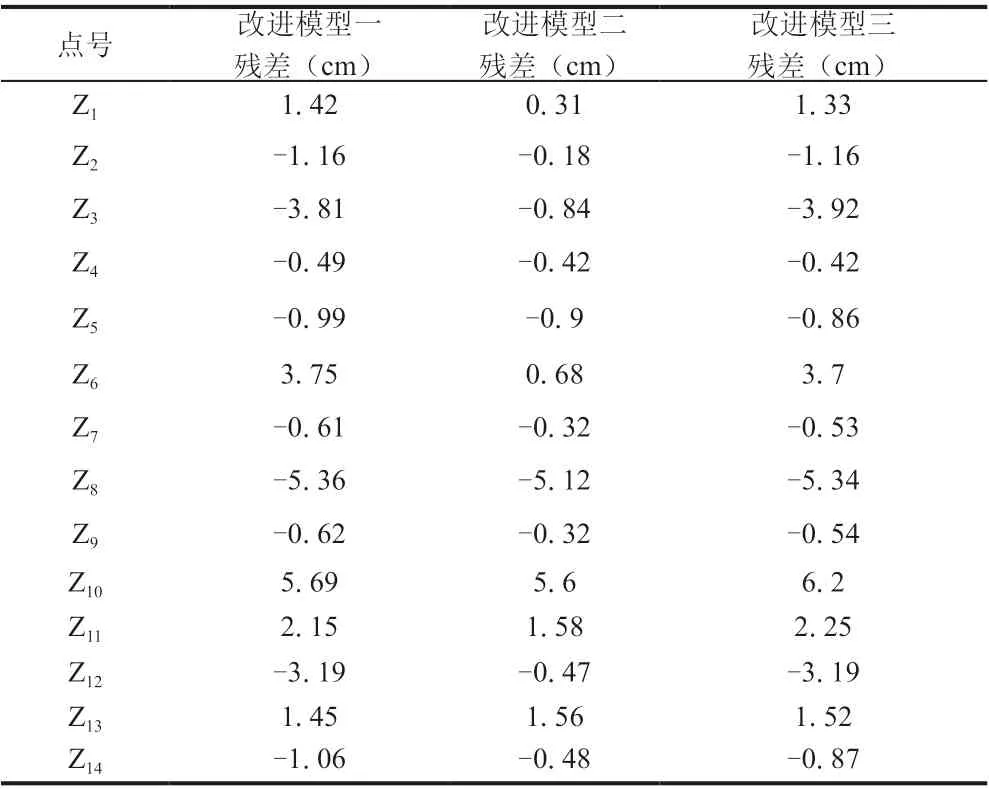
表5 三种模型的残差表

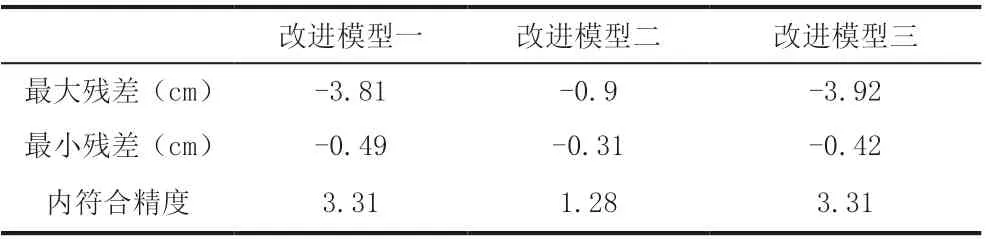
表6 控制点精度

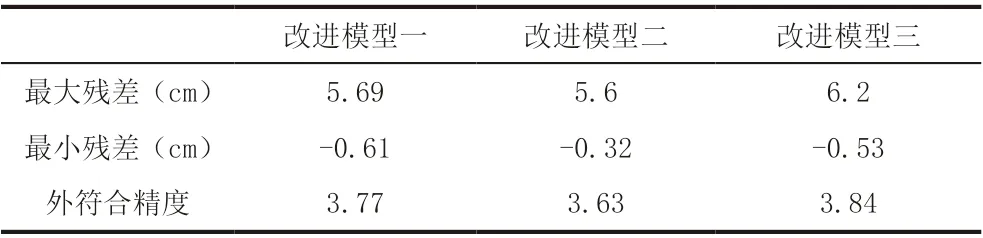
表7 未知点精度

表6、表7 为不同转换模型下控制点与未知点的最大残差、最小残差及内、外符合精度参数值。三种模型的内符合精度以改进模型二为最佳，外符合精度三个模型比较接近，但以改进模型二为最低。从单个测点残差值来看，改进模型二转换所得的结果中所有的控制点残差值均低于1cm，而未知点的残差值低于1cm 的测点占比达到42.9%，同样是三个转换模型中占比最高的。

综上可知，从整体测点及单个测点的精度来看，多项式曲面改进转换模型二为最优法，更适用于起伏路段。

4 结论

本文基于某公路项目中的平坦路段与起伏路段，布设GPS 平面控制网，采用最大残差绝对值及内、外符合精度值综合评估模型精度，得出结论：（1）在平坦路段，最大残差绝对值及内、外符合精度特征参数值均以二次曲面最小二乘优化法为最低，采用该模型进行转换更适合平坦地形。（2）在起伏路段，多项式曲面改进转换模型二所得的结果中，所有的控制点残差值均低于1cm，而未知点的残差值低于1cm 的测点占比达到42.9%，是三种模型中占比最高的，内、外符合精度亦是最低，因此，采用改进模型二更适合起伏路段。