多方分层远程态制备*
2019-11-12彭家寅
彭家寅
内江师范学院 数学与信息科学学院,四川 内江 641199
1 引言
量子纠缠是量子力学和量子信息理论中的重要概念,量子信息处理中许多最迷人之处都来源于纠缠的性质[1]。一方面,纠缠会引起非局域关联,这与现实的经典理论相悖[2]。另一方面,它也可用作量子信息处理中新的物理资源,如量子密码学[3]、量子对话[4]、量子密集编码[5]、量子计算[6]等。1993年,Bennett等人[7]首次提出了一种称为隐形传态的非常有趣的量子方法,它允许人们通过雇佣Einstein-Podolsky-Rosen(EPR)对作为量子通道,将一个单个粒子未知量子态安全地、忠实地从一个发送者传输给一个远程的接收者,而无需将该态本身在空间中直接物理传送。此后,相关研究工作被广泛报道,并在理论[8-16]和实验[17-18]方面都取得了重大进展。作为隐形传态的一种变体,远程态制备(remote state preparation,RSP)[19-20]这个新概念被提出来了,在这种新协议中,利用与量子隐形传态相同的量子信道就可能以比隐形传态更小的经典通信成本去远程制备一个已知量子态(通常称该态为目标态)。然而,在RSP中,欲被制备的量子态之所有信息都暴露给发送者。为了克服这个缺点,联合远程量子态制备(joint remote state preparation,JRSP)[21]被提出了。它主要处理如下情景的问题:被制备量子态的全部信息由位于不同地点的两个或更多的发送者共享,远程的接收者必须与所有发送者合作才能制备目标态。自2000年Pati[19]提出以Bell态为信道的第一个RSP协议以来,以不同量子态为信道的许多RSP 和JRSP 协议被提了出来,如Brown 态[22]、EPR 对[23]、GHZ(Greenberger-Horen-Zeilinger)态与GHZ 型态[24-25]、W 态与W 型态[26]、八粒子团簇态[27]、高维态[28]等。
到目前为止,几乎所有关于多方RSP 和JRSP 协议都限制在对称的情形,其所有的接受者都以相同能力重构发送者的原始秘密态。更一般的RSP 或JRSP 方案应该涉及不同参与者的权力之间的不对称,其中只有参与者的特定子集可以通过合作来恢复秘密量子态。最近,Shukla等人[29]讨论分层量子通信问题,并提出了分层联合远程态制备协议,其中发送者在空间分离的其他发送者和若干代理商之间分配量子态,并按代理商重构发送者的原始量子态之能力对代理商们进行分层。高层的代理商不需要帮助就能恢复发送者发送的量子态,而低层的代理商需要其他所有代理商合作的情况才能重构原始秘密态[30]。2011年,Wang等人[9]提出了一个以多粒子纠缠态为信道的多方分层量子信息分裂之方案,其代理商被分为两层,每层的代理商之人数原则上是任意的。虽然文献[30]提出了一个以五粒子团簇态为信道的非对称五方JRSP 协议,但还没有对这个非对称问题进行深入的研究,特别地,至今还未见多方非对称的RSP协议的报道。
本文基于Wang 等人[9]和Shukla 等人[30]的思想,提出了一个利用多粒子纠缠信道和经典通信的多方不对称RSP 方案,它包含两层的代理商S1={Bob1,Bob2,…,Bobn}和S2={Cindy1,Cindy2,…,Cindym}。为了恢复发送方(Alice)的单量子秘密状态,Bob们中的任何人需要其他Bob们和Cindy们中的任何一人的协作,而Cindy 们中任何人则需要所有其他代理商的协作。也就是说,不同层的代理商具有不同的权限来恢复目标状态,这种类型的RSP 称为分层远程态制备。值得注意的是代理商的协作是基于单量子测量和经典通信,它们不需要进行任何非局域操作。
2 多方分层远程态制备
假设发送者Alice 打算帮助她的代理商Bob1,Bob2,…,Bobn,Cindy1,Cindy2,…,Cindym制备一个任意单粒子态:

被Alice、Bob们和Cindy们预先分享的量子信道是如下一个(1+n+m)-粒子的图态。

其中,粒子A属于Alice,粒子Bi属于Bobi(i=1,2,…,n),粒子Cj属于Cindyj(j=1,2,…,m)。对每个粒子Bi和Ci(i≠1)都施行一个Hardamard门运算。

它可将式(2)的图态变成如下形式[34]:
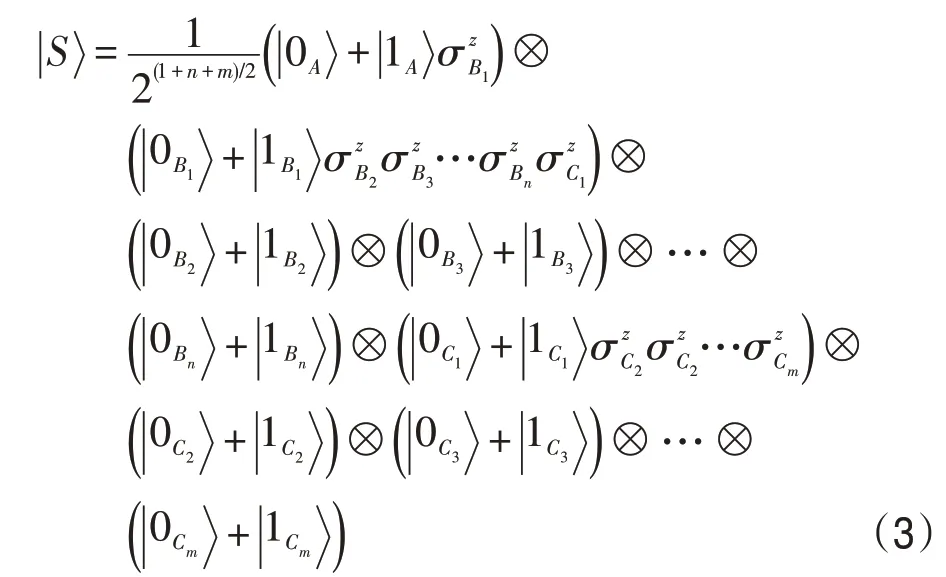
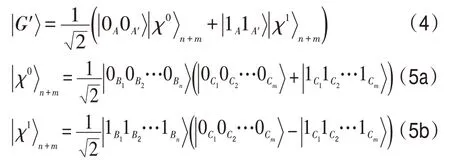
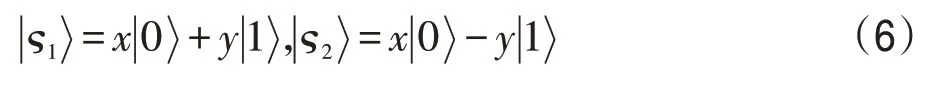
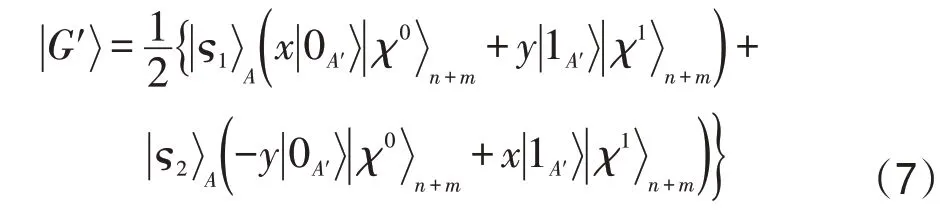
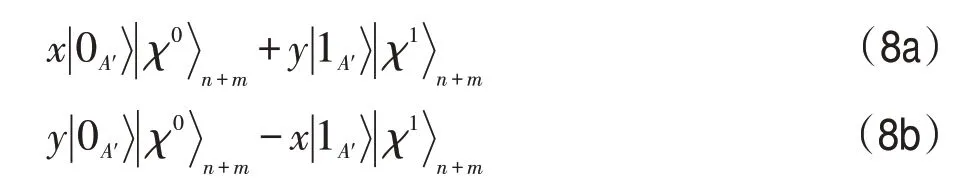
为了使方案成功的概率为1,接下来的处理就是机智的,因为采用了前馈测量策略。具体地说,在这一步中,Alice 的正确行动主要取决于前一步的测量结果。即,当Alice的测量结果为时,她需要对粒子A′施行如下酉运算:


换言之,利用基:

和基:

分别将式(8)表示成:

值得注意的是,在第二次测量中,Alice使用了前向反馈测量技术。也就是说,测量粒子A′的基的选择本质上分别取决于先前对粒子A的测量结果。从等式(11)知,在Alice 对粒子A和A′的测量后,她的代理商们的粒子将塌陷为下列态之一:

更详细地,Alice对粒子A和粒子A′的测量结果PMA和PMA′及代理商们的塌陷态S之间的关系如表1。

Table 1 Relation between measurement results and collapse states表1 测量结果与塌陷态之关系
非克隆定理[30-32]只允许一个量子处于秘密态,因此n+m个代理中的任何一个,但不是全部,都可以恢复这个态。
首先,假定代理商们同意Bob1去恢复Alice 的原始秘密态。利用Wang 等人[9]的表示方法,可以将态和态表示为:
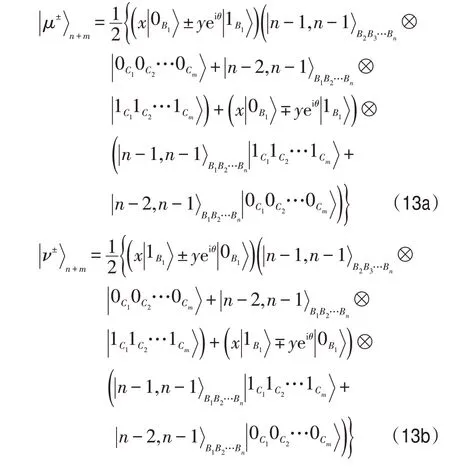
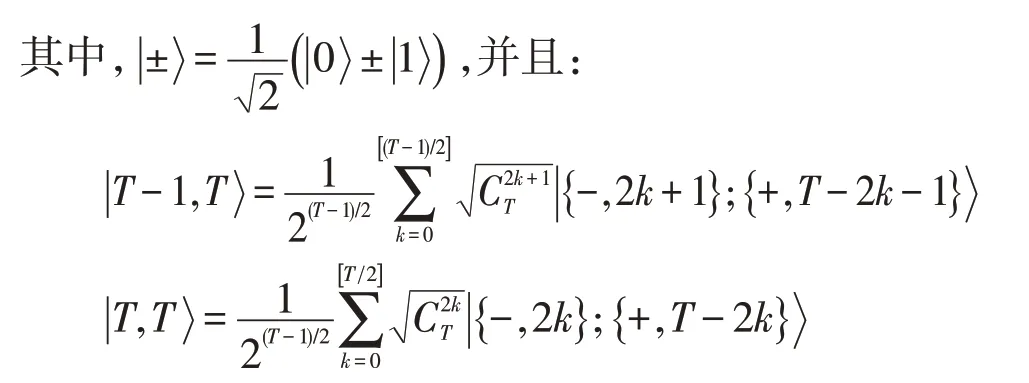
这里T是一个整数,表示的整数部分,=T!/K!(T-K)!(K=2k,2k+1)是组合系数,表示包括K个“-”和T-K个“+”的全部对称态,例如由等式(13)知,除Bob1外的所有n-1个Bob和Cindy们中的任意一个人(不失一般性,假设为Cindy1)就能协助Bob1去成功恢复Alice 的原始秘密态。具体地,Bob1外的所有n-1 个Bob 都利用基去测量他们的粒子。同时,Cindy1利用基去测量他的粒子C1,并将他们的测量结果通知Bob1。为了重构Alice的秘密态,Bob1需要对自己粒子B1执行一个适当的酉运算,这个酉运算来自集合,其中I为恒等算子,而σx、σy、σz为Pauli算子。令VC和VS1分别表示Cindy1和Bob们获得的测量结果之值,那么记VS=VC⊕VS1,⊕为模2的加法。当然,态集被编码为值“0”,而被编码为值“1”。Bob1的恢复算子U与Alice、Cindy1及其余Bob们的测量结果(PMA,PMA′,VS)之间的关系见表2。

Table 2 Relation among operator U and PMA、PMA′and VS表2 算子U 与PMA、PMA′和VS 间的关系
现在,考虑代理商们支持Cindy1重构Alice 的原始秘密态利用文献[9]的表示方法,态和态可以表示为:
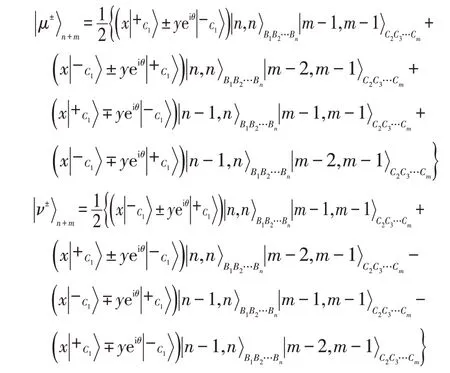
从上式可知,Cindy1能重构Alice 的原始秘密态当且仅当n个Bob 和其他m-1 个Cindy 都用基去测量他们的粒子,并播报其测量结果。换言之,Cindy1需要其他所有的代理商的帮助才能恢复Alice的原始秘密态为此,Cindy1需要对自己的粒子C1执行酉运算集合{H,σxH,iσyH,σzH}中之一,这里H是Hardamard门。令分别表示Bob们和其余Cindy们获得测量结果的值,那么Cindy1的恢复算子U同Alice和其他代理商的测量结果(PMA,PMA′,)之间的对应关系见表3。
Table 3 Relation among PMA PMA′,, and U表3 PMA PMA′、、 与U 的关系

Table 3 Relation among PMA PMA′,, and U表3 PMA PMA′、、 与U 的关系
综合上述分析,可以得到这样的结论:对于重构Alice的原始秘密态而言,Bob们中任何人仅需要Cindy们的任何一个人和其他Bob们的帮助就可以完成任务;而Cindy们中的任何人则需要所有的Bob和其余的全体Cindy 之帮助才能完成量子任务。因此代理商们获得Alice 的秘密态的权限被分层,所有Bob们相对于所有Cindy们来说处于高层位置。这个结果可以如下理解:Alice进行两次单粒子测量后,测量结果为,而Bob 们和Cindy们的单粒子密度矩阵分别为:

3 讨论与结论
多方的RSP 方案对于一般的量子分布式计算和量子网络通信非常重要,JRSP 协议的安全性高于RSP协议。因此自然会问,本文的HRSP(hierarchical remote state preparation)方案是否可以修改为分层JRSP 方案(hierarchical joint remote state preparation,HJRSP)。事实上,考虑以下情景:假设发送方Alice1和Alice2与她们的(n+m)个代理商Bob1,Bob2,…,Bobm,Cindy1,Cindy2,…,Cindym事先共同分享等式(4)中(2+n+m)-粒子的图态,其中粒子A属于Alice1,粒子A′属于Alice2,粒子Bj属于Bobj(j=1,2,…,n),粒子Cj属于Cindyj(j=1,2,…,m)。为了帮助代理商中的任一人制备秘密态,Alice1利用等式(6)中的基对其粒子进行投影测量,并公布她的测量结果。收到Alice1的信息后,Alice2采用前馈测量策略对自己粒子执行等式(9)、等式(10)中的酉运算U1或U2,并公布测量结果。剩下的任务只需与第2章的相应工作重复就行了。通过这种方式,得到了多层分层JRSP协议。
现在,来讨论本文方案抵抗一些窃听攻击的安全问题。由于非克隆定理[31-32]和纠缠成对性[30],窃听者窃听秘密态的唯一办法是采取拦截-重发攻击。尤其是窃听者截获从Alice 发送给所有Bob 们和所有Cindy 们的所有粒子(B1,B2,…,Bn,C1,C2,…,Cm)(因为Bob们或Cindy们中的哪一个将拥有秘密状态在协议之前没有指定),然后把假粒子(记B′1,B′2,…,B′n,C′1,C′2,…,C′m)发给Bob们或Cindy们。为了尽可能地保持Bob们和Cindy们之间的量子相关性,窃听者可以在图态中准备(n+m)个伪量子位。

然而,Alice 和她的代理们之间的量子关联被破坏了。Alice和代理们通过对他们自己或接收的量子位进行适当的局域测量,就能很容易地检测这种攻击。例如,他们都选择单粒子计算基础作为测量基础,在窃听者的攻击下,Alice和代理们的测量结果之间就会没有相关性。然而,在无窃听的情况下,Alice的测量结果总是与Bob们的测量结果相关,而与Cindy们的测量结果相反。由于纠缠是成对的,因此总是可以通过检查量子纠缠信道的量子相关性来检测窃听攻击[33]。为了检查安全性,将会牺牲部分纠缠信道。事实上,大多数量子通信协议都需要使用量子相关,并牺牲部分纠缠信道来检查针对窃听者的拦截的安全性。
在Wang 等人[9]和Shukla 等人[30]的工作基础上,提出了多方分层的远程态制备协议,其中代理们分为两个层次(S1和S2),两个层次的代理人数原则上可以是任意的。该方案中的大量参与者对于本文协议在分布式量子计算和量子网络通信中的应用是非常有意义的。在本文协议中,S1层的代理商比S2层的代理商具有更强的恢复Alice 秘密态的能力,且这个多方HRSP方案可以被修改为分层JRSP协议。本文中提出的协议也是安全的,防止窃听,并且可视为是对常规(对称)RSP 和JRSP 方案的补充[18-29]。与现有非对称量子信息分裂方案[12]和需要多粒子集体操作的分层量子通信方案[29]相比,本文方案不涉及非局部操作(多粒子操作)。作为本文方案中量子信道的图态是量子信息科学中非常重要的量子资源[9],它的制备也是所给出的HRSP 和HJRSP 方案物理实现的关键。据文献[34]的工作,通过线性光学技术可以有效地产生图态。此外,在量子秘密分发过程中使用前向反馈测量技术确保了本文协议成功的概率为1。
