船舶三维声弹性模拟软件的并行优化策略*
2019-11-12吕小敬蒋令闻陈德训杨广文1
吕小敬,刘 钊,蒋令闻,陈德训,杨广文1,
1.国家超级计算无锡中心,江苏 无锡 214072
2.中国船舶科学研究中心,江苏 无锡 214082
3.国家并行计算机工程技术研究中心,江苏 无锡 214083
4.清华大学,北京 100084
1 引言
船舶三维声弹性分析理论与方法研究弹性浮体与水介质的耦合振动及由此引起的声辐射、声散射和声传播问题。在此基础上开发的船舶三维水弹性声学分析软件THAFTS-Acoustic(three-dimensional hydroelastic analysis of floating traveling structures)可以实现船内振动传递与船舶水中辐射声场的统一计算与分析,具有良好的工程应用性[1-2]。
三维声弹性力学的研究在改善船舶运动性能与安全性,控制船舶振动噪声及提高水下隐身性能等一系列工程问题中有广泛的应用需求和发展前景。1984年,Wu[3]建立了二维水弹性力学理论,将船体结构简化为非均匀Euler 梁或Timoshenko 梁。Price 和Wu[4]将结构动力学理论与三维船舶运动势流理论相结合,提出了广义流固耦合边界条件,开创性地发展了适用于波浪中任意三维可变形体承受内的三维水弹性力学理论。Du 等[5]发展了零航速三维脉动源Green函数快速计算方法,并建立了完善的三维航行船体线性水弹性力学频域分析理论的数值计算方法。Zhou等[6]在三维水弹性理论及程序基础上,发展了带速航速、计及海面及海底边界影响的船舶三维声弹性理论,同时开发了一套较完整的可用于解决复杂船舶结构低中频段声弹性问题的数值模拟软件。
三维声弹性理论及软件功能已日益完善,如何提高软件计算能力,完善软件计算复杂结构、复杂海洋水声信道环境的功能,实现多工况、大任务计算的能力已迫在眉睫。而近年来,高性能计算蓬勃发展,如结合高性能计算理论及超级计算机的海量计算资源,对现有程序进行并行升级和优化,提高软件的大规模高效率计算性能,成为了一个具有重要应用价值的研究课题[7-15]。
本文针对三维声弹性理论算法特点,结合“神威·太湖之光”计算资源及体系架构,完成了三维声弹性软件THAFTS-Acoustic 广义水动力系数计算模块(THAFTS-Acoustic-hycof)核心算法的多级并行。使用某典型算例对多级并行优化策略进行测试和验证,测试结果表明:完成多级并行后,核心算法代码段获得18 倍的加速效果,且程序具有良好的并行可扩展性,能够支持THAFTS-Acoustic进行超大规模和更高精度的并行计算,为进一步改善我国船舶运动性能、安全性、震动噪声以及水下隐身性能指出了一条可行的道路。
2 三维声弹性算法及应用软件简介
2.1 三维声弹性算法概述
频域内船舶声弹耦合动力学方程为:
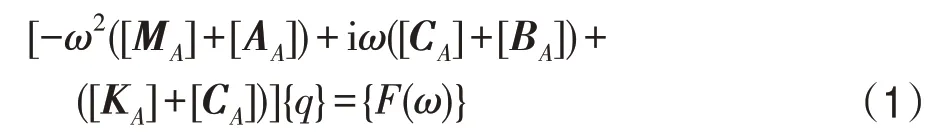
其中,ω为频率,MA为结构干模态广义质量矩阵,CA为广义阻尼矩阵,KA为广义刚度矩阵,[AA]为干模态附连水质量矩阵,[BA]是干模态附连水质量阻尼矩阵,[CA]为广义恢复力稀疏矩阵。
流场内的速度势及基本运动方程满足:
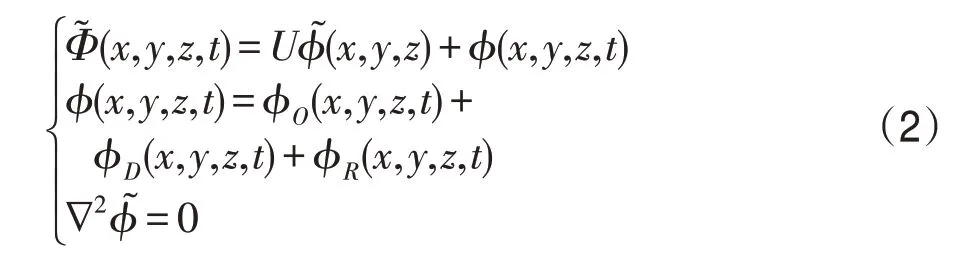
其中,ϕ(x0,y0,z0,t)为相对于固定坐标系的流场中总的速度势,为船舶恒速直线航行所诱导的相对于平衡坐标系的非均匀稳态流场速度势,ϕO(x,y,z,t)、ϕD(x,y,z,t)、ϕR(x,y,z,t)分别为入射波速度势、反射波速度势及辐射波速度势。
考虑到船体在无粘、无旋的可压声介质中,应满足Bernoulli方程(Cauchy-Lagrange积分):

结合各阶模态的辐射波对应的流固耦合边界条件:
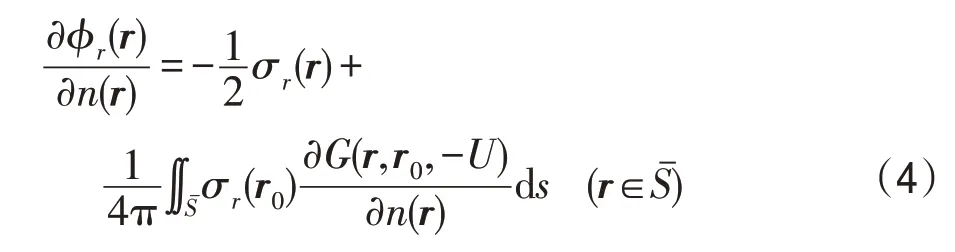
采用频率法求解时,r阶广义力F的表达式可展开为:

其中,Arj、Brj、Crj分别为流体作用在结构上的附连水质量矩阵、附连水阻尼矩阵及广义恢复力系数矩阵,S为结构平均湿表面。
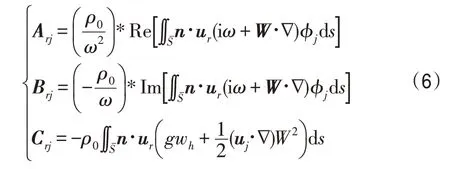
采用有限水深环境中声波Green函数(7)求解流场内的速度势及基本运行方程可得:
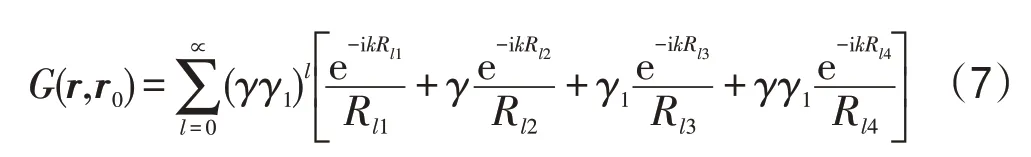
辐射波速度势的表达式为:

采用Hess-Smith 等强度源方法,将船体湿表面(与流体接触的表面)离散成N块四边形面元,则:
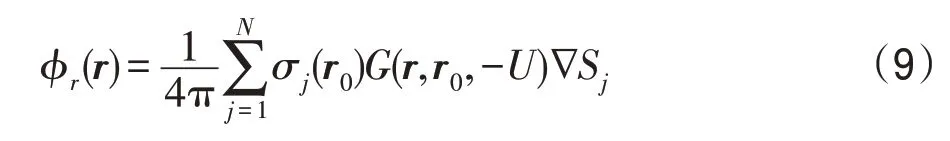
各阶模态的辐射波速度势与主坐标响应满足:

根据模态叠加原理,由式(1)~式(10)求出各阶干模态主坐标响应qr(r=1,2,…,m)后,带入船舶结构振动方程,即得结构振动响应及流场内辐射声性能。
三维声弹性计算涉及多场耦合、多物理量、多核心段,单一的并行模式根本无法满足所有计算热点的高效并行,因此需要针对该软件算法特点,构建多层次、多类型异构并行模型,支持数据并行与任务并行结合的混合并行模式,扩大程序并行度,保证各并行层次上的负载平衡,同时结合神威太湖之光超级计算机体系架构,研究恰当的多级混合并行算法实现,充分发挥众核处理器的超高计算性能。
2.2 三维声弹性软件流程
三维声弹性软件包含三个模块:flxbd、hycof、hyelas。flxbd模块对输入的数据进行预处理,生成广义水动力系数计算模块hycof所需数据;hycof模块通过计算格林函数及其偏导数,计算源强和速度势,得到水动力系数等参数;hyelas模块根据水动力参数求解广义流固耦合动力学方程,生成后处理所需数据。其中广义水动力系数计算模块hycof和hyelas计算量较大,目前仅实现了一维湿面元并行,程序并行效率低,无法满足湿面元/模态平方依赖或者更高依赖的函数,且超过64进程时,会出现倒加速情况。本文针对hycof 模块内不同计算过程及各计算过程数据依赖关系,考虑计算过程复杂度,考虑多级并行时各计算过程衔接及过程间数据衔接,实现了广义水动力系数计算模块多级异构并行,提高程序并行度及可扩展性能。THAFTS-Acoustic软件流程图如图1所示。
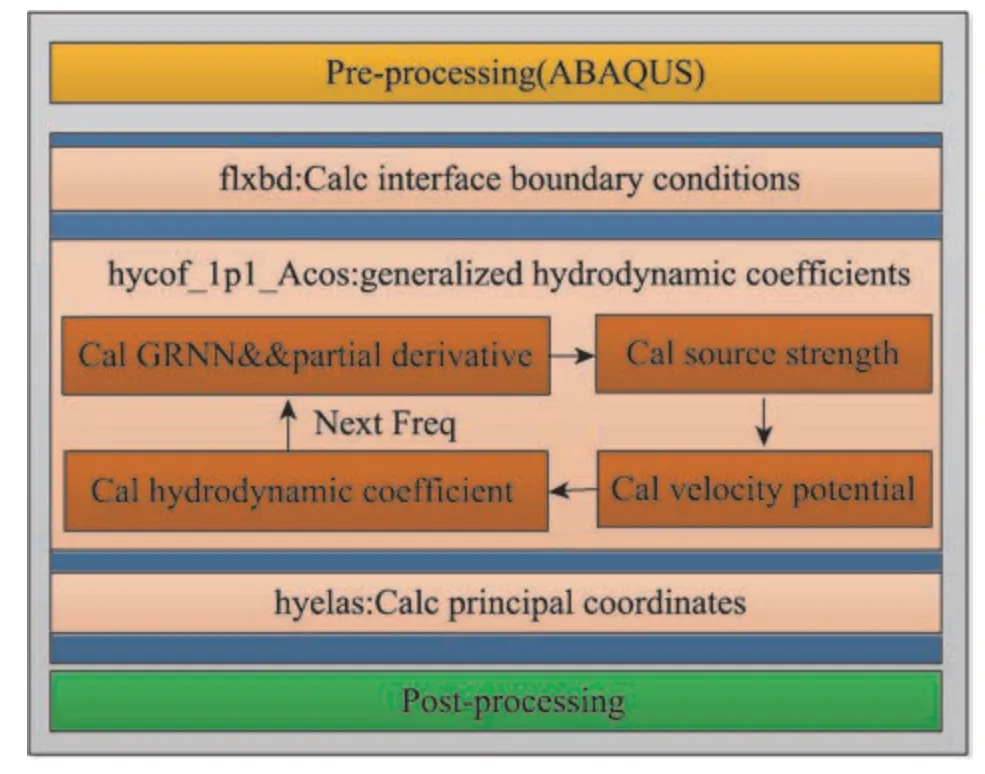
Fig.1 Flow chart of THAFTS-Acoustic software图1 THAFTS-Acoustic软件流程图
3 神威·太湖之光超级计算机系统简介
3.1 SW26010处理器
神威·太湖之光超级计算机全机由40 960 块SW26010 异构众核处理器、20 480 块计算板节点组成,共有10 649 600 个计算核心,系统峰值性能为125.4 PFlops,已连续4次蝉联TOP500榜首。SW26010处理器架构如图2所示。
SW26010异构众核处理器包含4个核组,每个核组包含1 个主核和64 个从核,核组内提供8 GB 本地内存。从核局部(local data memory,LDM)存储空间大小为64 KB。从核访问LDM 速度较快,因此众核优化的关键是减少从核访主存次数,提高LDM 利用率。
3.2 “神威·太湖之光”并行方法
“神威·太湖之光”计算机系统语言环境包括基础语言系统、并行编程语言接口、用户使用环境及基础编程环境,支持消息并行模型、共享并行编程模型、加速并行编程模型,同时支持4种异构并行方式:主从加速并行、主从协同并行、主从异步并行、主从动态并行。异构并行方式如图3所示。
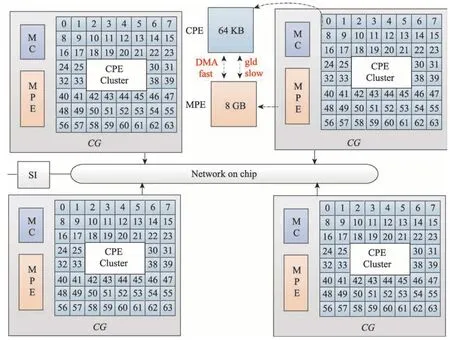
Fig.2 Architecture of SW26010图2 SW26010处理器架构
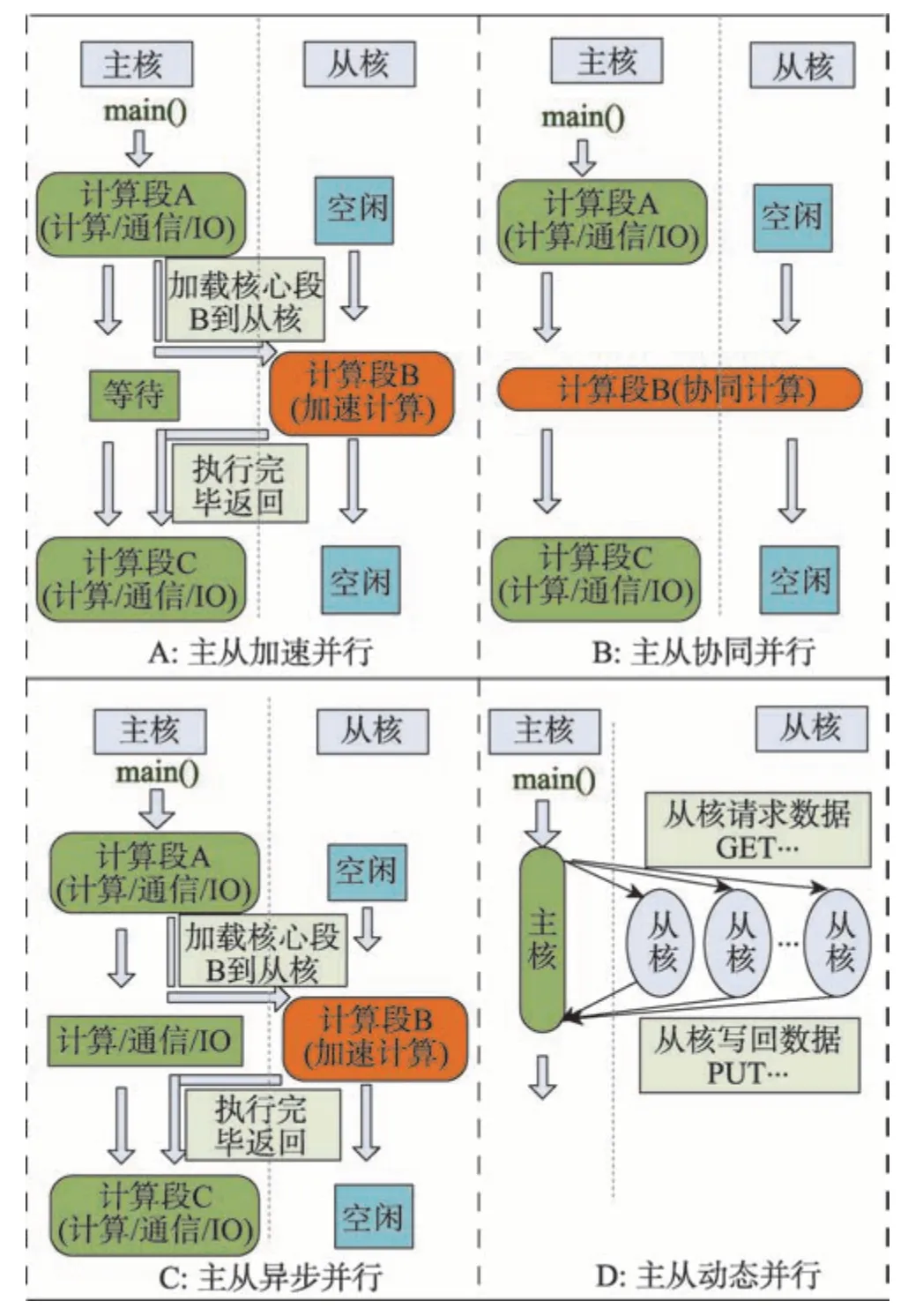
Fig.3 Heterogeneous parallel method on Sunway TaihuLight图3 “神威·太湖之光”计算机系统异构并行方法
主从加速并行中,计算核心通过加速线程库加载核心段到从核上完成加速计算,主核等待加速任务结束后完成通信、IO(input/output)和部分代码计算;主从协同并行时,主核作为一个核心,与从核一起完成核心任务计算;主从异步并行时,主核完成计算、通信、IO操作,从核完成核心加速,可实现计算通信隐藏、计算IO 隐藏,优化效果明显;主从动态并行主要应用于从核计算任务时间不固定或者某些任务并行的程序。
4 三维声弹性软件多级异构并行算法实现及优化
本文基于异构并行模型,根据船舶三维声弹性算法特点,以不同计算阶段计算密度为特征,以变量依赖关系分析为基础,在以数据预处理和基本变化为主的前后端计算阶段采用MPI(message passing interface)消息传递并行;在核心计算阶段,研究多级异构主从异步算法,增大程序并行度,采用分块策略和通信计算隐藏策略,实现不同并行层次上的负载平衡。多级并行方案如图4所示。
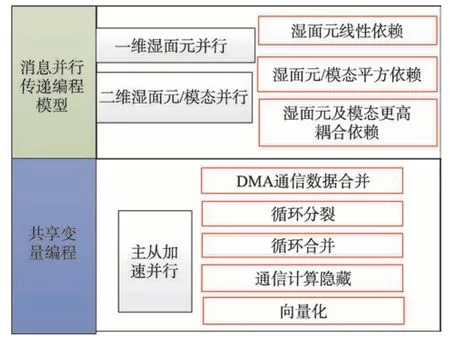
Fig.4 Multi-level parallel schematic of THAFTS-Acoustic-hycof图4 三维声弹性软件多级并行图
4.1 一维湿面元级并行算法实现
假定船体离散后总湿面元数为IXX,总进程数为numprocs,一维数据并行时数据并行方式如图5所示。
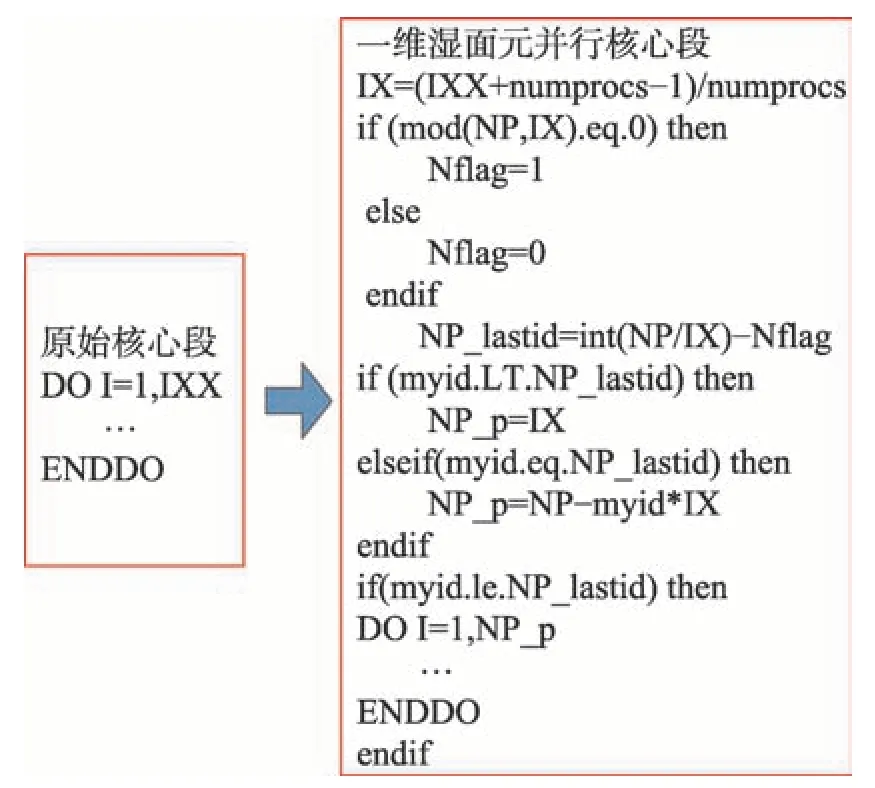
Fig.5 One-dimensional parallel strategy of wet surface element图5 一维湿面元级并行策略
采用一维湿面元并行操作较为简单,对程序的修改最少,进程间通信次数和通信总的数据量可以达到最小,便于实现多级并行中各过程间数据衔接及多工况程序耦合。
4.2 二维湿面元并行及模态并行算法实现
一维湿面元并行可以较为简单地实现计算量线性依赖湿面元数的函数,然而对于平方依赖或更高依赖湿面元的函数效果却不是很好,如计算格林根数偏导VIN(IXX,IX)及求解源强SV(IXX,MODE),随着湿面元数及求解模态数增加,程序并行效率降低。以由格林函数偏导求解源强为例,同一列VIN分布在不同的进程中,主进程需要通信收集列主元行号,通信完成列主元行与当前行交换,完成处理后,仍需要与其他进程通信。当并行规模较小时,这种并行方案有一定并行加速效果,但是随着进程数增多,通信量急剧增大,加速效果越来越差,甚至出现倒加速。因此需要设计更为合理的并行模式。
本文采用二维湿面元/模态分块并行解决上述问题。假设行进程数为NPROW,列进程数为NPCOL,行进程分得块大小为NNB,列进程分块大小为NNM,各进程分得的行数为NNP,列数为NNQ,MYROW为行进程号,MYCOL为列进程号,MYID为当前进程组号,数据划分方式如图6所示。
二维分块并行后,可以对进程进行分组操作,同时某进程完成NNB行×NNM列计算后,在与其他进程进行块通信同时,可计算下一个NNB行×NNM列块,便于实现通信和计算隐藏。
对于某些计算量与湿面元数/模态数成平方依赖的函数,采用二维湿面元并行程序扩展性更好,同时便于利用更大的进程数。
4.3 基于athread的众核并行算法实现及优化
SW26010处理器上每个从核配备了用户可控的64 KB局部数据高速缓存(LDM),支持gld/gst直接离散访问主存及DMA批量数据访问主存,并将数据放置在LDM 中。从核访问主存访问效率很低,需要数百个时钟周期,而从核访问LDM 数据仅需要数个时钟周期。因此,众核并行性能提升的关键是充分利用从核LDM,减少访存次数,降低访存开销及通信开销。
4.3.1 DMA通信数据的合并

Fig.6 Two-dimensional block parallel strategy of wet surface element/mode图6 二维湿面元/模态分块并行策略
减少通信和访存开销的最直接方法就是减少通信次数,减小需要通信的数据和增大单次数据通信的数据长度。因此可以将需要通信的数据进行合并和计算,减少通信次数,提高通信带宽利用率。
三维声弹性求解速度势时,观察到格林函数数组GRNN(IXX,5,IX)与AR_A(IXX)数组,按照LDM大小分块拷贝到从核时,需要6次通信。将格林函数数组GRNN与AR_A数组合并为一个数组后,通信次数可降低为1,且可增大单次数据拷贝量,既减少了访存,又增大通信带宽利用率。
4.3.2 循环分块及循环合并
异构众核并行及优化中,需充分利用从核局存访存性能,将数据尽量多地放到LDM 中,而SW26010 芯片的从核LDM 仅有64 KB,实际课题中无法将内层循环相关物理量一次性拷贝到LDM 中,访主存则加速性能较低。本文根据从核LDM 大小,选择合适的分块并行方式,提高从核访存性能。
实际应用课题中,核心段一般包含多重循环,如果仅按照最外层循环做任务划分,易造成从核间负载不均衡。本文采用外层循环合并方式,增大程序并行度,提高程序的并行性能。循环分块及循环合并实现如图7所示。

Fig.7 Loop tile and loop collapse multicore parallelization scheme图7 循环合并及循环分裂众核并行方案
4.3.3 通信计算隐藏
对于众核加速计算程序,提高DMA 带宽,降低从核DMA 通信时间是提升性能的另一关键策略。本文采用计算和通信隐藏方案,具体实现过程如图8所示。
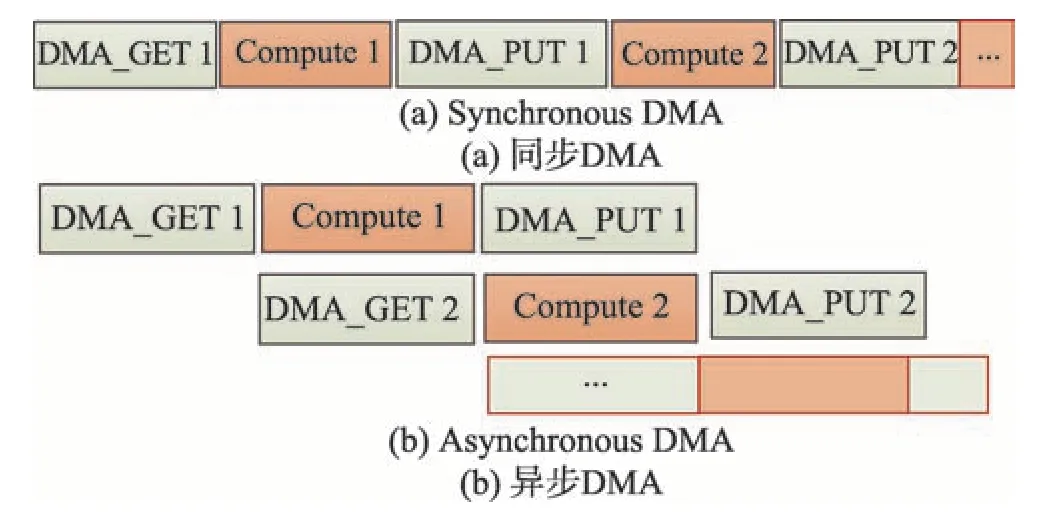
Fig.8 Over hiding parallel scheme of communication and computation图8 通信计算隐藏并行方案
4.3.4 向量化
SW26010处理器具备256位向量寄存器,可一次处理4 次浮点计算,8 次整型计算。因此一条SIMD(single instruction multiple data)指令相当于一个小的循环,可以减少指令数及由循环引起的控制相关,充分利用SIMD扩展结构提高性能。
SIMD编程在标准C的基础上扩展得到了6种标准数据类型intv8、unitv8、int256、uint256、floatv4 及doublev4,标准变量需要通过显式SIMD 内部函数调用、扩充的数据类型等实现SIMD的功能。
hycof 核心段内主要为复矩阵运算,计算两个复数乘c=c+a*b时,假设初始c=(c1+c2i),a=(a1+a2i),b=(b1+b2i),则c=(c1+a1*b1-a2*b2)+(c2+a1*b2+a2*b1)i。然而神威太湖之光系统没有与复数类型匹配的扩展数据类型,必须将复数矩阵转变为标准扩展数据类型。复数分实部虚部,一个complex*16 相当于两个real*8。本文采用如下复数向量化方案,如图9 所示:两个复数可扩展为一个doublev4 扩展数据类型,之后通过SIMD 内部函数调用,可分离数据,得到复数计算实部虚部,再通过向量间运算,实现复数的运算操作,提高程序运算性能。
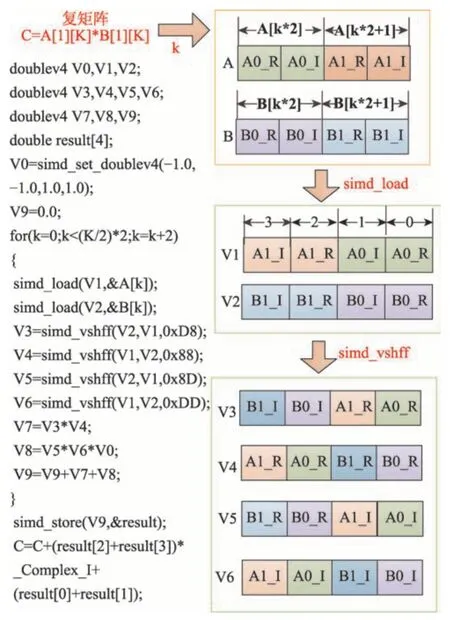
Fig.9 SIMD parallel scheme of three-dimensional acoustic elastic complex matrix图9 三维声弹性复矩阵SIMD并行方案
4.4 I/O优化
由于I/O 性能的增长速度跟不上系统本身处理能力的发展,I/O 性能成为高性能并行计算的主要性能瓶颈。THAFTS-Acoustic 软件中采用文件保存临时计算数组,当数据的读写量不大时,能够满足需求,但是随着数据规模的增大,对I/O 提出了更高的要求。本文采用以下三个优化策略:(1)针对内存占较大的临时数组,程序中的格林函数GRNN 采用全局变量在各过程间传输数据,删除变量读写I/O;(2)数值模式中所有通信域内的进程均参与数据文件的输出,各进程将其负责的数据写入独立文件,提高I/O 并发度;(3)进程分组收集数据,将各进程组内数据合并,减少写文件I/O次数,增大单次I/O数据量。
5 并行性能测试及算例验证
5.1 软件并行性能测试
本文采用湿面元数5 678,模态数1 500,计算频率数为3的左舷半球壳的算例。
5.1.1 多级异构并行加速性能
本文基于神威太湖之光系统,采用64进程及256进程两个并行规模,对二维湿面元/模块并行程序及多级异构并行程序相较一维湿面元并行程序的加速性能进行了初步的测试,如图10所示。
64 进程测试时,二维湿面元/模态并行程序相较原始一维湿面元并行程序整体加速2.37 倍,多级异构并行程序相较原始一维湿面元并行程序整体加速5.54 倍。随着进程数的增大,采用二维湿面元/模态并行及多级异构并行的优势更为显著。
本文采用4~512 进程测试多级异构并行程序的MPI 扩展性能,测试结果如图11 所示。多级异构并行规模小于256 进程时,具有较为理想的加速效率,但是随着数据规模的扩大,并行效率降低。这是由于算例湿面元数是5 678,当进程数大于256时,进程内数据量减少,计算开销与通信、IO 开销比明显降低,并行效率下降。
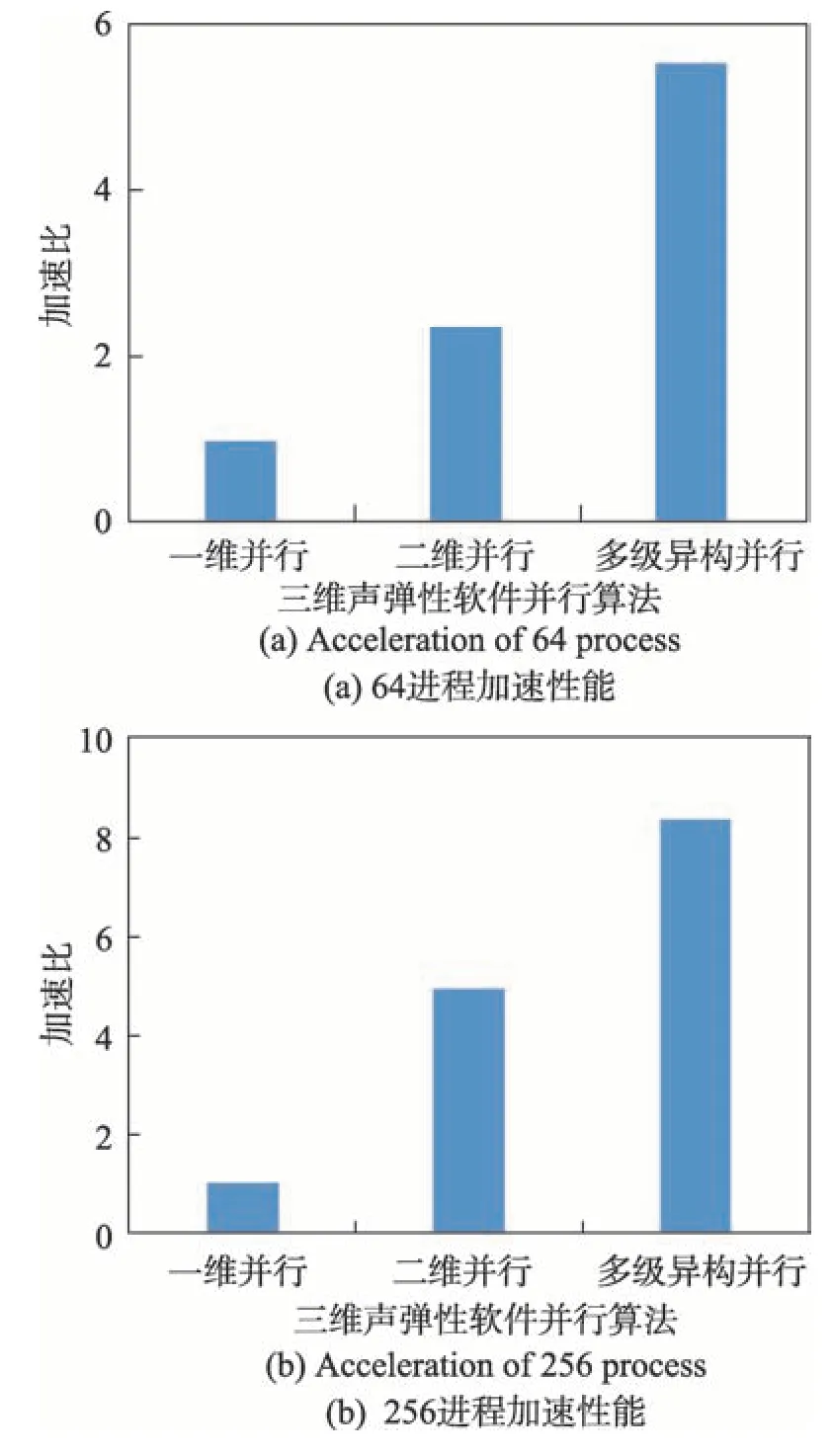
Fig.10 Multi-level parallel acceleration performance图10 多级并行加速性能
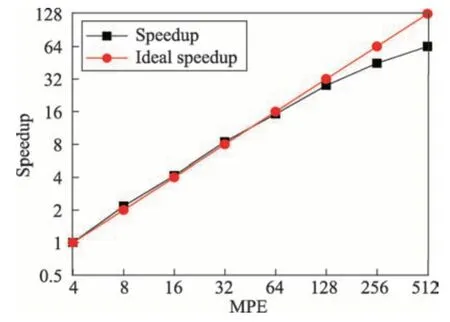
Fig.11 Strong scalability of multi-level heterogeneous parallelization图11 多级异构并行强可扩展性测试
5.1.2 众核加速性能测试
本文采用湿面元数5 678,模态数1 500,计算频率数3 的左舷半球壳的算例。基于神威太湖之光系统,采用256进程测试众核并行加速性能。测试的对象包括源强求解及速度势求解两个过程。程序众核加速性能如表1所示。

Table 1 Multicore parallel acceleration ratio of kernel functions in THAFTS-Acoustic-hycof表1 THAFTS-Acoustic-hycof核心函数众核并行加速比
采用向量化、通信与计算隐藏、循环合并及循环分裂等优化方法完成众核并行后,程序求解速度势加速17.7 倍。源强求解核心函数以块为单位并行,求解中存在大量的进程间通信,在计算完成后需要将数据块使用进程组通信发送给其他进程,而通信过程无法使用众核进行加速。在通信成为瓶颈的情况下,源强求解函数仍然获得了6.6 倍的整体加速效果。
5.2 软件正确性验证
本文采用湿面元数5 678,模态数1 500,计算频率数3的左舷半球壳的算例,验证多级异构并行程序正确性。3个频率点(每个频率点计算2次,共计算6次)的物理量附连水质量、附连水阻尼相较原始程序的协方差如图12所示。
由图12可知:6次计算的附连水质量协方差均在E-16 量级,附连水阻尼的协方差均在E-14 量级,误差范围合理。多级异构并行结果与软件初始版本计算结果一致。
本文采用经典的受径向单位集中力作用下舷间充水双层弹性球壳结构声辐射的算例模型进行软件正确性验证。计算模型如图13 所示:该计算模型存在解析解及THAFTS 软件模拟解,具体可参考文献[6]。
采用零航速,无界流场,内球壳半径0.5 m,内球壳壁厚1 mm,外球壳半径0.65 m,外球壳壁厚0.3 mm,内外球壳体密度7 800 kg/m3,杨氏模量2.1×1 011 N/m2,泊松比0.3,干模态阻尼比0.01,内外场流体密度1 025 kg/m3,内外场流体声速1 500 m/s。内球壳湿面元网格边长约0.05 m,外球壳湿面元网格边长约0.065 m。计算4个场点的辐射声压。软件求解和解析计算结果比对情况如图14所示。

Fig.12 Correctness verification图12 正确性验证

Fig.13 Double layer concentric sphere and coordinate system图13 双层同心球和坐标系
测试结果表明,多级并行后,三维声弹性计算程序是正确的,可应用到实际工程领域。

Fig.14 Comparison of calculation results图14 计算结果对比
6 总结与展望
三维声弹性力学的研究可广泛应用在改善船舶运动性能与安全性的应用领域。在本文中,完成了三维声弹性核心求解模块THAFTS-Acoustic-hycof的多级异构并行工作。主要包括以下几点:根据程序算法复杂度,完成了THAFTS-Acoustic-hycof 的一级湿面元并行、二级湿面元/模态并行,设计了三维声弹性源强及速度势求解过程的众核并行及优化,包括DMA 通信数据合并、循环分裂及循环合并、通信计算隐藏及SIMD等。测试结果表明,三维声弹性多级并行程序具有良好的并行加速比和众核加速性能,能够有效地发挥SW26010 国产众核处理器和神威•太湖之光超级计算机的强大计算能力,从而大大缩短实际工程应用的项目周期,加速改善我国船舶运动性能、安全性、震动噪声等关键性能,提高船型整体设计研发效率。
未来将在以下方面开展工作:
(1)THAFTS-Acoustic-hycof 软件的频率并行:目前测试阶段计算频率个数有限,但潜在频率数比较大,因此如何实现频率并行与湿面元、模态并行,众核并行结合是进一步提高程序并行效率的关键。
(2)断点恢复及容错功能:完善THAFTS-Acoustichycof在大规模异构并行计算机系统硬件故障容错和重启动功能,保证计算结果的正确性和可靠性。
(3)THAFTS-Acoustic 软件的全过程并行及优化:开发THAFTS-Acoustic-flxbd 前处理模块并行算法及程序,开发THAFTS-Acoustic-hyelas后处理模块的多级并行及优化。
