基于滑移预测的月球车路径规划研究

周兰凤 杨丽娜 方 华

(上海应用技术大学 上海 201418)

0 引 言

月球车作为探测月球的主要工具之一，它最重要的任务就是月球路径规划[1]。月球环境复杂多样使月球车路径规划十分困难，有效地避免陷入危险地形、缩短最优路径长度和节约路径规划时间是月球路径规划研究的重点。月球地形的湿度和坡度的不同，产生的滑移率不同，一定程度使路径规划产生偏移，有效的预测滑移有利于找到最短最优路径。既包含传统的算法(A*算法[2]，遗传算法[3])，也带有一些新型的智能算法(蚁群算法[4]，神经网络算法[5]，粒子群算法[6])，经典遗传算法存在搜索时间长、易陷入僵局、算法复杂度高的不足，无法求得最优化路径。

本文针对现有的遗传算法容易陷入局部最优解的问题，综合考虑月球地形环境信息，通过加入地形因素的滑移预测综合通过性代价函数。使用MATLAB仿真实验，保持地形参数不变，调整滑移通过性函数参数，对比100次实验仿真结果，综合遗传算法进化代数少于传统遗传算法。改进后的遗传算法提高了月球车路径规划的平滑性，缩短了路径的长度，节省了路径规划的时间和进化次数。

1 综合遗传算法

1.1 遗传算法路径规划模型建立

本文遗传编码采用实数编码，遗传算法中每1个染色体对应1个解决方案，在路径规划过程中，基因是由起点、终点和路径规划经过的若干中间点组成。如图1所示，起点(X1,Y1,Z1)、终点(Xn,Yn,Zn)和n-2个中间点构成1条携带从起点到目标点的路径规划信息的染色体。

图1 路径规划中有n个基因的1条染色体

因此，一条完整的机器人路径(P)就可以表示为若干条线段的有序组合，如下式所示：

P=∑Pi

(1)

式中：Pi表示第i段直线段的矢量表示。

1.2 初始种群的生成

本文中一条染色体由n个坐标点组成，即一条可通过性的路径，也称这个路径为一条染色体。从起点出发，随机选择可通过性的邻节点，取其坐标加入染色体中，依次循环，直到找到终点结束。重复上面操作，达到初始目标种群数量，终止循环。

1.3 遗传操作

遗传算法是一种仿生的全局优化概率搜索的自适应算法[7]。其算法结构设计需要预设的参数有：初始种群数量、最大进化迭代数、交叉概率和变异概率等。 算法过程包括选择、交叉、变异三个阶段。将遗传算法应用到路径规划规程的问题中，固定参数的交叉概率和变异概率适应算法可以更好地找到最优路径[8]，通过不断的迭代，最终得到问题最优解。

本算法采用优胜劣汰选择策略，即用部分优秀个体，根据一定策略实时替换部分低劣个体[9]，保持个体的最优化。

(1) 交叉操作是遗传学中基因重组的重要过程，也是遗传算法产生新个体的重要途径[10]。本文采用部分映射方式进行染色体的交叉操作，生成两个随机数m、n，将x、y染色体位于m和n之间的基因片段互换。交叉概率公式为：

(2)

式中：Pc表示动态路径规划中交叉概率；Pcmax表示交叉概率的最大值；Pcmin表示交叉概率的最小值；Fmax表示最大适应度值；Fmin表示最小适应度值；Fc表示两个要交叉个体中较大的适应度值。

(2) 变异操作类似遗传学中的基因突变，更新过程中一条染色体上的点坐标发生随机变化，即产生变异个体。变异概率公式为：

(3)

式中：Pm表示动态路径规划中变异概率；Pmmax表示变异率的最大值；Pmmin表示变异概率的最小值；Fmax表示最大适应度值；Fmin表示最小适应度值；Fm表示要变异个体的适应度值。

2 适应度函数设计

适应度函数作为评判种群中个体的存活率的标准之一，依据目标函数而确定，路径规划过程中，适应度函数的值越大越好。在本文路径规划中路径最短和进化代数最小是首要目标。除此之外，本文还加入了地形评估综合通过性代价函数。地形评估综合通过性代价函数是综合了地形的一些主要因素，如阶梯障碍、地形粗糙程度、坡度等，同时还加入了最主要的滑移因素，从而在滑移预测的基础上形成了地形评估综合通过性代价函数。该函数可以准确描述地形上两点之间的综合通过能力。这里将上述地形评估综合通过性代价函数f(p,n)，并入遗传算法的适应度函数，采用综合遗传算法进行路径规划。

设置节点p到节点n的基因片段的地形综合代价函数如下：

f(p,n)=f1×ftrav(p,n)+f2×frisky(p,n)+

f3×fguide(p,n)+f4×fsmooth(p,n)

(4)

式中：ftrav(p,n)为从节点p到节点n的可通过性代价函数(一般取值为0或1)；frisky(p,n)为潜在危险性代价函数；fguide(p,n)为综合考虑了地形的角度和坡度等因素的指导性路径代价函数，它与地形的坡度角度有关；fsmooth(p,n)是描述路径平滑程度的代价函数，取值为固定常数值f1、f2、f3、f4分别为ftrav(p,n)、frisky(p,n)、fguide(p,n)和fsmooth(p,n)的权值，一般将它们取为同一固定的常数值。

综上，在滑移预测的基础上形成了地形评估综合通过性代价函数f(p,n)，将它与遗传算法融合，改变其适应度函数，构造成一个具有滑移预测地形评估综合通过性代价的适应度函数f′(p,n)，本文称为综合适应度函数，公式如下：

f′(p,n)=f(p,n)+f0(p,n)

(5)

式中：f′(p,n)为综合遗传算法的函数的适应度函数；f(p,n)地形综合代价函数；f0(p,n)基于遗传算法适应度函数。

3 仿真实验

基于MATLAB 2014环境下建立虚拟三维地形环境，虚拟三维空间抽象为网格或栅格，然后设置参数，如路径中的起点、终点、高度以及初始种群的数量。本次实验设置种群个数30，最大进化迭代次数200。从图2可以看出，该三维遗传算法路径规划，比二维的栅格模型更直观有效。

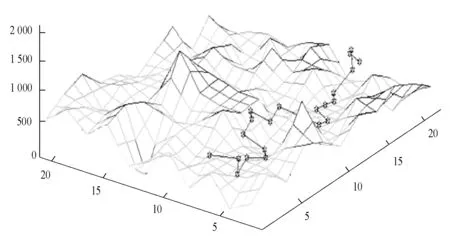
图2 基于遗传算法的三维模型路径规划图

3.1 遗传算法与综合遗传算法实验对比

本文遗传算法和综合遗传算法(简称IGA)一次进化代数及综合适应度变化图如图3、图4所示。从图3可以看出，基本遗传算法进化到10代左右就进入了局部最优解，50代之后更新最优解，140代得到1次实验最优解，综合适应度值为130。从图4可以看出，进化代数20次时得到1次试验最优解，综合适应度值为125，一定程度上缩短了路径规划时间，提高了工作效率。

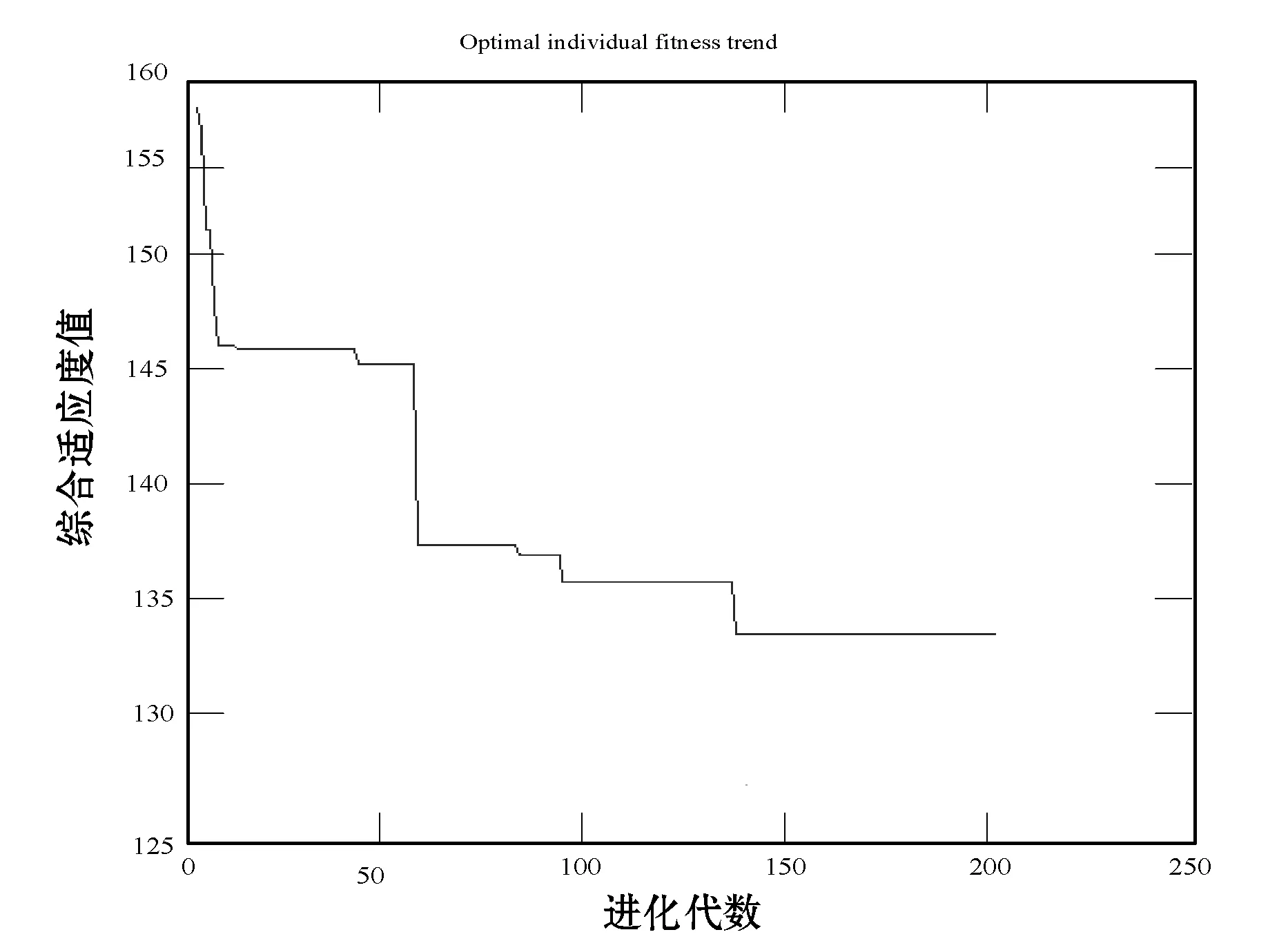
图3 遗传算法

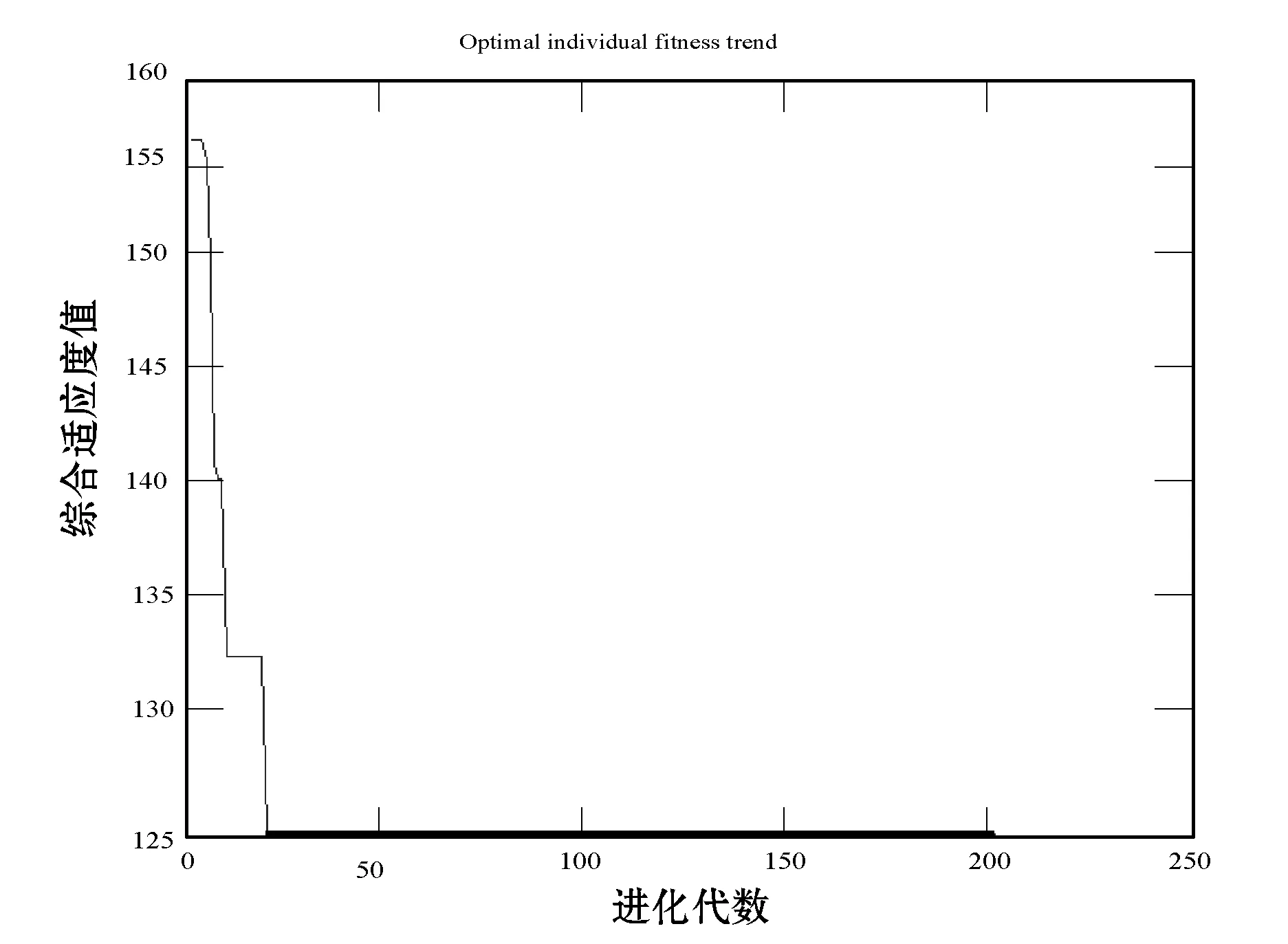
图4 综合遗传算法

为了进一步证明算法的合理性，规避偶然因素对算法的影响，对两种路径规划算法分别实验100次，统计实验结果如表1所示。可以看出，综合遗传算法的平均最大路径比遗传算法最大路径缩短了34.7%、平均适应度值提高了12.4%、平均进化代数缩小了49.2%。

3.2 改进蚁群算法与综合遗传算法对比

通过设置相同参数的滑移预测函数和地形通过性代价函数，使用改进蚁群算法和综合遗传算法各实验n次，各随机抽取两种算法的6次试验进行对比，结果如表2所示。

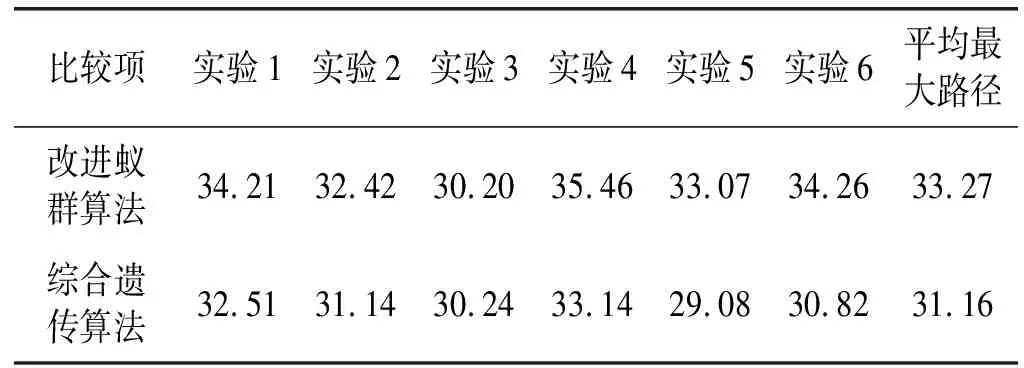
表2 两种算法的最大路径长度比较 km

可以看出，综合遗传算法比改进蚁群算法在最大路径长度性能更加优化。

综合两个实验得知，通过引入带有滑移预测函数可通过性的代价函数，使得算法在寻找路径的过程中，更加注重路径的曲折性且避免机器人搜索产生无效的移动距离。由表1可以看出，综合遗传算法在找到最优的路径的时间效率上也得到了一定的改善。因为在考虑了滑移预测的地形可通过性函数的基础上，综合遗传算法路径规划的搜索能力更加优化，不会在一些不合理的路径上继续进行后续的搜索。

4 结 语

由于遗传算法应用在路径规划问题上，存在诸多问题，如收敛效率低、陷入局部最优解、复杂度高等，引入了地形综合代价函数进行适应度函数设计，根据综合适应度值动态获得交叉算子和变异算子值，提出了一种综合遗传算法路径规划算法。通过实验仿真得知, 改进的综合遗传算法在搜索最优路径、时间复杂度上比传统遗传算法都有了更好的优化。这也说明本文在算法上的创新应用，在某种程度上弥补了传统遗传算法的缺点。加入可通过性滑移预测算法的遗传算法，为月球车避障提供有效方法，一定程度上提高了路径搜索的效率、节约了时间成本、规避了地形风险。