“小量近似”在高考和竞赛中的应用
2019-11-11余建刚
余建刚


摘 要:本文由一道2019年全国高考理科数学题引出“小量近似”在高考和竞赛中的应用,简要地阐述了小量近似的定义及数学来源、小量近似的近似程度及典例说明.
关键词:小量近似;物理竞赛;高考
2019年全国高考理科数学Ⅱ卷第4题,题目如下:
2019年1月3日嫦娥四號探测器成功实现人类历史上首次月球软着陆,我们航空事业取得又一重大成就,实现月球背面软着陆需要解决的一个关键技术问题是地面与探测器的通讯联系.为了解决这个问题,发射了嫦娥四号中继卫星“鹊桥”.鹊桥沿着围绕地月拉格朗日L2点的轨道运行,L2点是平衡点,位于地月连线的延长线上.设地球质量为M1,月球为M2,地月距离为R,L2点到月球的距离为r,根据牛顿定律和万有引力定律,r满足方程M1(R+r)2+M2r2=(R+r)M1R3.
设α=rR,由于α的值很小,因此近似计算中3α3+3α4+α5(1+α)2≈3α3,则r的近似值为( )
A.M2M1R B.M22M1R C.33M2M1R D.3M23M1R
无独有偶,第32届全国中学生物理预赛题也曾有类似的数学处理方法,题目如下:2011年8月中国发射的宇宙飞船“嫦娥二号”在完成探月任务后,首次从绕月轨道飞向日地延长线上的拉格朗日点,在该点,“嫦娥二号”和地球一起同步绕太阳做圆周运动.已知太阳和地球的质量分别为MS和ME, 日地距离为R.该拉格朗日点离地球的距离x满足的方程为,由此解得x≈.(已知当λl时,(1+λ)n≈1+nλ)
此二题在计算过程均涉及到小量近似的处理方法,其实小量近似在中学物理竞赛中,是比较普遍的数学处理方法,屡见不鲜.但对普通的高考生而言或许有点陌生.故笔者撰写本文简述“小量近似”在高考和竞赛中的应用,以期达到抛砖引玉之效.
1 小量近似的定义及数学来源
在数学中,我们把以零为极限(即无限趋近于零但又不为零)的变量,称为无穷小量,即小量.小量近似,就是指在运算中为了简化运算结果,但又不影响结果正确性的前提下,将一些相对较小的项忽略不计的运算方法.
数学上,有一个有名的公式称泰勒Taylor展开公式(或称泰勒公式),将任意一个函数写成多项式的形式,各项分别为零阶小量、一阶小量、二阶小量…….公式如下:
f(x0+Δx)=f(x0)+f ′(x0)Δx+f″(x0)2!Δx2+……+f(n)(x0)n!Δxn+o(Δxn)
(注:公式最后一项o(Δxn)表示剩下所有的项,相对于Δxn都是小量.)
常见函数在x0=0处的泰勒展开:
sinx=x-x33!+x55!-x77!+…+(-1)kx2k+1(2k+1)!+o(x2k+1)
cosx=1-x22!+x44!-x66!+…+(-1)k(2k)!x2k+o(x2k).
(1+x)μ=1+μx+μ(μ-1)2!x2+…+μ(μ-1)…(μ-n+1)n!xn+o(xn).
11+x=1-x+x2-x3+…+(-1)nxn+o(xn).
ex=1+x+x22!+…+xnn!+o(xn).
ln(1+x)=x-x22+x33-x44+…+(-1)n-1xnn+o(xn).
注:不是所有的函数在所有的位置都可以进行泰勒展开.只有当高阶项越来越小且趋近于0时才能用泰勒展开的前几项之和来近似原函数的值.
高中阶段能够见到的小量近似公式全部可以用泰勒公式展开得到.用泰勒公式展开,忽略高阶小量,只取一阶近似,可得到物理竞赛中常见的如下近似公式:
sinx=x;cosx=0;ex=1+x;ln(1+x)=x(1±x)n=1±nx(以上公式中的x均为小量)
2 小量近似的方法
(1)对一个小角量θ来说,它的正弦值、正切值与其本身相等,即θ≈sinθ≈tanθ.小角量θ所对应的弧长与弦长也相等.
(2)在研究一个普通量时,可以将小量忽略不计.如计算常量A与小量Δ β之和,可以忽略后面小量,结果直接为A.
(3)在研究小量时,可以忽略比它阶数高的小量.比如Δβ是小量,Δβ2、Δβ3、 Δβ4等都是比Δβ更高阶的小量,我们就可以将其忽略不计.
3 小量近似的近似程度
在物理竞赛中应用小量近似,应近似到什么程度? 物理竞赛中的小量近似,既要体现出小量对函数的影响,又要达到简化运算的目的,所以绝大多数情况,泰勒公式展开后,取一阶近似即可,二阶和更高阶的小量可忽略.但有两种情况例外:
(1)若函数本身为小量,为了体现更高阶小量对函数的影响,则可保留更高一阶的小量.
(2)若取一阶近似无法体现出小量对函数的影响,则可取更高一阶的近似.比如单由度保守力场中,在平衡位置附近对势能函数的展开,设势能函数为U(x),平衡位置为x0,在平衡位置x0附近展开势能函数则有U(x)=U(x0)+U(1)(x-x0)+12U(2)(x-x0)2+O(x-x0)n
由于势能函数的导数值在平衡位置取零,即U(1)(x-x0)=0 ,所以势能函数一阶小量为零,若只取一阶近似,则无法体现出小量对势能函数的影响,于是二阶小量12U(2)(x-x0)2也应保留.
4 小量近似的应用典例
(1)小角度近似
对一个小角量θ来说,它的正弦值、正切值与其本身相等,即当θ→0时,θ≈sinθ≈tanθ. 譬如,证明小角度近似下单摆可以近似为一个简谐运动.证明如下:
证明:如图1,在很小角度下物体受回复力:
F回=-mgsinθ≈-mgθ=-mgxL=-kx,
具有简谐运动回复力的特征,k=mgL,
周期为:T=2πmk=2πLg.
又如光学中近轴光学入射,观察水中的鱼或玻璃中物体的视深公式.
证明:如图2,由光的折射定律:1×sini=n×sinr
根据小角度近似,有sini≈tani=OAh′,sinr≈tanr=OAh
整理,得1×OAh′=n×OAh ,
因此,像的位置h′=hn
(2)一阶小量近似
物理过程运算关系式常以多项式形式出现,这时可以运用以下的近似处理(1±x)n=1±nxx1.其依据就是当要求精度不高的时候,应当略去 x 的高阶小量,而保留 x 的一阶量,泰勒公式展开,略去高阶小量,只保留一阶小量.
譬如,本文开篇所提到的32届预赛题,已知拉格朗日点处“嫦娥二号”和地球一起同步绕太阳做圆周运动.太阳和地球的质量分别为MS和ME, 日地距离为R.求该拉格朗日点离地球的距离x满足的方程为和位置x .我们不妨用小量近似求解一下.
解:根据万有引力定律和牛顿第二定律,有
Gmsm(R+x)2+GmEmx2=mω2(x+R)
GmsmER2=mEω2(x+R)
联立,得 GmsmR(1+xR)2+GmEmx2=GmsR2(1+xR)
由于xR,则(1+xR)-2=1-2xR即
mE x2≈ms R2·3xR,解得x = (mE 3ms )13R
(3)二阶小量近似
在小量近似处理中,当取一阶近似时,无法体现出小量对所求函数造成的影响,因而要继续去二阶小量近似.譬如下题:
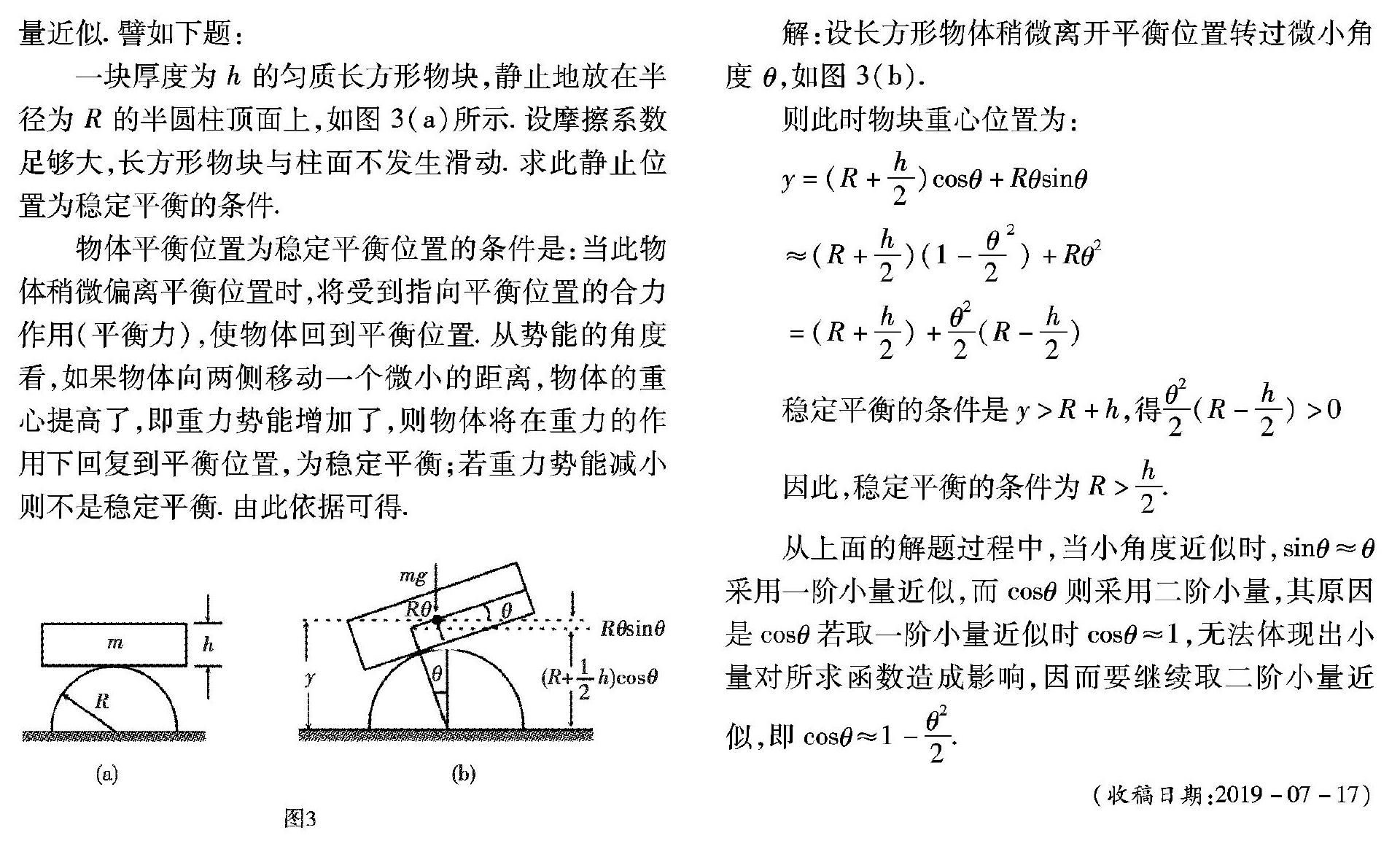
一块厚度为 h 的匀质长方形物块,静止地放在半径为 R 的半圆柱顶面上,如图 3(a)所示.设摩擦系数足够大,长方形物块与柱面不发生滑动.求此静止位置为稳定平衡的条件.
物体平衡位置为稳定平衡位置的条件是:当此物体稍微偏离平衡位置时,将受到指向平衡位置的合力作用(平衡力),使物体回到平衡位置.从势能的角度看,如果物体向两侧移动一个微小的距离,物体的重心提高了,即重力势能增加了,则物体将在重力的作用下回复到平衡位置,为稳定平衡;若重力势能减小则不是稳定平衡.由此依据可得.
解:设长方形物体稍微离开平衡位置转过微小角度 θ,如图 3(b).
则此时物块重心位置为:
y=(R+h2)cosθ+Rθsinθ
≈(R+h2)(1-θ22)+Rθ2
=(R+h2)+θ22(R-h2)
稳定平衡的条件是y>R+h,得θ22(R-h2)>0
因此,穩定平衡的条件为R>h2.
从上面的解题过程中,当小角度近似时,sinθ≈θ 采用一阶小量近似,而cosθ则采用二阶小量,其原因是cosθ若取一阶小量近似时cosθ≈1,无法体现出小量对所求函数造成影响,因而要继续取二阶小量近似,即cosθ≈1-θ22.
