面向智慧城市的多精度群智感知定价机制研究

王 忱

（南京邮电大学，南京 210003）

1 研究背景

利用移动设备进行信息感知，即移动群智感知，可以融合人的主动感知能力和设备丰富的传感器资源，因而具有信息种类丰富、感知水平高和部署成本极低的优势，将成为5G的重要业务之一。群智感知是智慧城市的一个重要的解决方案。例如，群智感知会方便政府部门监测河流污染状况。监测任务会通过基站定期向河流覆盖区域进行发布，用户随后可以上传反映河水水质和周围工业情况的照片，服务器在收集到所有用户的感知信息后，通过一定的检测算法确定污染情况和污染源。

由于用户参与群智感知需要花费一定的网络流量、设备电量、交通成本甚至机会成本，因此需要设计一定的群智感知激励机制，主要包括拍卖、信誉和定价三种方式。由于定价机制具有客观性和直接性，近来越来越多的学者聚焦在定价激励机制的研究上。例如，文献[1]将定价机制用于指纹定位系统。文献[2]将基于用户参与感知概率的定价机制用于车辆系统中。文献[3]和[4]在服务器有限预算背景下，基于到任务现场的距离成本，设计了激励用户参与感知的定价。文献[5]和[6]也假设服务器的预算是有限的，并基于Stackelberg博弈设计了Q学习定价机制，文献[3]研究了智慧城市背景下的群智感知应用，但采用了社会关系这样一种单一的激励方式。本文中，我们基于对智慧城市应用的认识，假设服务器的预算是一个固定的预期值，基于Stackelberg博弈研究了多精度群智感知的最优定价的存在条件，并设计了基于Q学习的优化定价方法，能有效提升算法的用户适应性、成本节约性和感知安全性。

2 基于Stackelberg博弈的定价收益模型

下面在Stackelberg博弈模型的基础上，给出本文的定价博弈模型。假设感知精度i分为P级且表示为i=1，2，...，P，另有i=0表示用户参与虚假感知，i=-2表示用户参与未参与感知。首先，服务器作为带头人发布定价策略，为保证定价的公平性，本文假设在同一时刻，服务器付给不同用户在同一感知精度i上的价格是相同的，均为y（i）。然后，用户作为跟随者选择一定的感知精度i，并付出感知成本，第j个用户的成本记为

下面分别建立建立用户端和服务器端的定价收益模型。在用户端，考虑用户进行虚假感知时可能给自身带来收益，则有可能使未参与感知的成本用户j选择参与精度为i的感知所期望获得的收益记为，令和将用户期望得到的定价记为ey（i），则有：

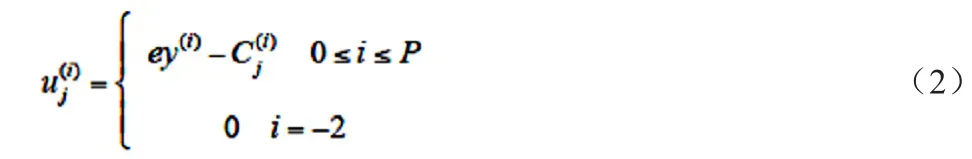
在服务器端，由于服务器存在评估错误概率e，服务器只能认为评估后的感知精度才是服务器的收益，且评估后的虚假感知会被服务器自动舍弃，因而带给服务器的收益为0。因此，如果用户j选择的感知精度为i，服务器经评估后得到的收益为：

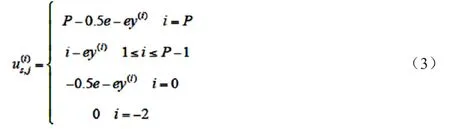
服务器在所有M个用户可能参与的群智感知任务中获得的总收益记为us，可表示如下：

3 多精度群智感知的最优定价存在条件

首先讨论单个用户参与的情况，从用户收益最大化出发，若要使该用户选择感知精度i，则用户收益应大于用户选择其他精度、不参与感知和参与虚假感知等情况。据此可以不加证明地得到如下的引理。

引理1：对于参与多精度群智感知的某一个特定用户j，激励他选择精度为的感知的充分必要条件是：

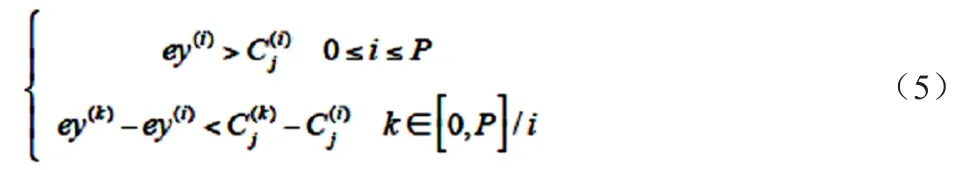
根据上述引理得到 ey（i）后，可以根据 ey（i）与 y（i）的关系得到 y（i）。

对于某一特定用户，最优定价应是使用户参与某种非虚假的感知、且服务器收益最大的定价。为使最大化，应使 ey（i）大于且尽可能地接近，这样能得到最大值的如下表达式：

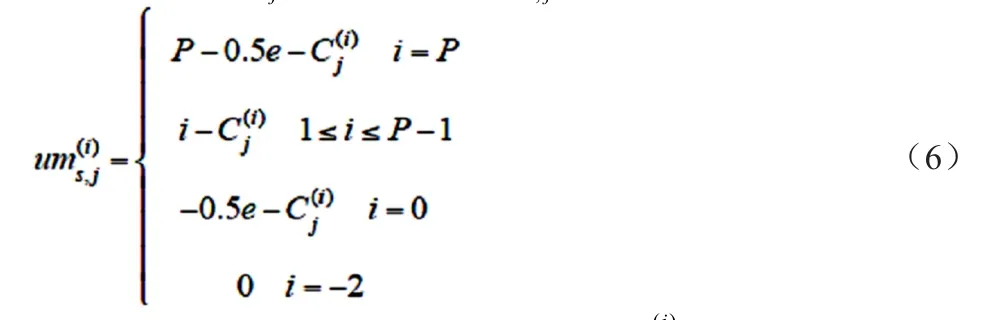
因此，应激励用户选择的精度i应使得最大。结合引理1，可以不加证明地得到如下的引理：

引理2：对于参与多精度群智感知的某一个特定用户j，最优定价应激励用户选择使最大的精度i0，且定价应满足如下的充分必要条件：

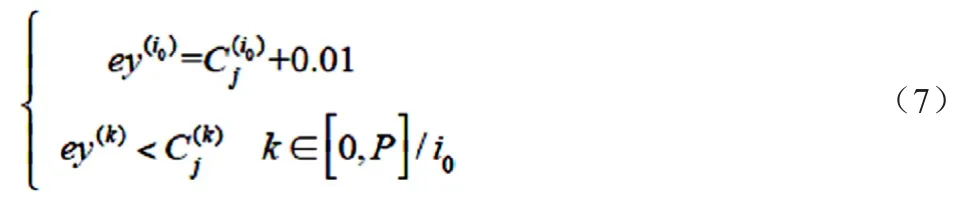
这里假设定价是离散的，且最小单位是0.01。

接下来讨论所有M个用户参与多精度群智感知的情况。若要使用户选择精度不小于i的感知，且服务器期望得到的总感知精度为U，从用户收益最大化出发，若要激励不少于个用户选择精度不小于i的感知，则这些用户的收益应大于选择其他精度、不参与感知和参与虚假感知等情况。据此可以不加证明地得到如下的定理。

定理1：对于参与多精度群智感知的所有M个用户，假设可以将用户按他们在感知精度i上的成本从小到大排序为，若要激励不少于个用户选择精度不小于i的感知，则定价应满足如下的充分必要条件：

若服务器期望从所有M个用户得到的总感知精度为U，最优定价应是使用户参与某种非虚假的感知、且服务器收益最大的定价。根据引理2，最优定价过程即寻找所有M个用户中感知精度与成本差最大的感知精度及其对应用户，与此同时，应使ey（i）大于且尽可能地接近。据此可以证明得到如下的定理。

定理2：对于参与多精度群智感知的所有M个用户和P个感知精度，假设可以将从大到小排序，并取出最大的n项为，对应的感知精度和i1+i2+...+in等于U，而这n项中最小的一项对应的感知精度和用户成本分别为ib和Cb。则最优定价可有下面的线性定价形式：

当ib≠P时

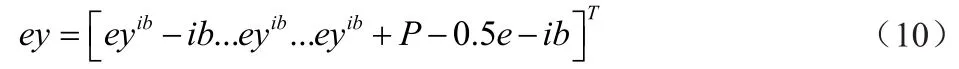
当ib=P时，

证明：根据假设条件，不论ib是否等于P，上面的期望价格ey都可以补偿选出的n个净收益最大项所对应的成本。对于其他项，我们有。然后，当ib≠P时，对于其他ib≠P的项有：

当ib=P时，对于其他i≠P的项有：

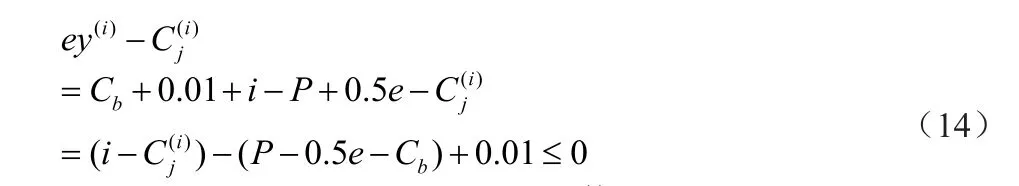
当ib=P时，对于其他i = P的项有：

因此，除了选出的n项，这些用户将不会选择其他感知精度，而且其他用户也不会选择任何感知精度或参与虚假感知。

4 不完全信息条件下的动态定价算法

在大多数智慧城市的应用场景中，潜在的感知用户数量及其感知成本都会随时间变化，可记为M（t）和。因此不能简单根据上面的最优定价方法来确定群智感知的定价。此时定价过程应该服从如下的动态定价过程：（1）在系统测试阶段，发布一个随机的定价，测试用户的选择；（2）服务器根据用户的选择，决定定价的滑动方向和滑动步长，该步骤会被迭代重复，直到定价趋于稳定；（3）在系统运行阶段，根据现场用户的响应再次动态调整定价。

根据上述讨论，该动态定价过程可以用Q学习算法来完成。Q学习是强化学习的一种，它有状态（state）、动作（action）、奖赏（reward）这三个要素。Q为动作效用函数，每个状态所对应的动作都有一个效用值。Q学习的训练公式如下：

其中，学习速率α越大，保留之前训练的效果就越小；折扣因子λ越大，记忆中的利益所占比重就越大。在定价学习过程中，从每个定价状态出发，只可能有增或减两种动作，分别表示为αr和αι，动作的奖励应为i（t+1）/（t+1）。我们现在令α=1，提出基于Q学习的滑动定价算法SPA，其过程如下：

（1）初始化及滑动区间的设定：固定虚假感知的期望价格为-1，而完全精度感知的期望价格ey（p）从最低定价0开始滑动，滑动范围从最低定价0到最高定价p-0.5e，单步滑动步长固定为最小值0.01，当ey（p）滑动至1-0.5e之后，ey（p-1）从0开始与ey（p）同时滑动，且总与ey（p-1）保持1-0.5e的差距。以此类推，当ey（2）滑动至1之后，ey（1）从0开始与ey（2）...ey（p）同时滑动，且总与ey（2）保持1的差距。

（2）滑动定价过程：将当前期望价格向用户群体中的某随机抽取的用户进行发布，如果该用户选择精度为的感知，则当前期望价格向量ey的奖励值增加i。如果当前所有价格的平均奖励值（即奖励值与被测试次数的比）大于或等于NU/M（N为当前测试过的总人数），则当前所有不为0的价格向低滑动一次，反之则向高滑动一次。如果该用户参与虚假感知，则进一步降低虚假感知的定价。对该步骤迭代进行M次。

（3）定价选取：从当前稳定价格的下方选择平均激励值大于或等于U的最低用户期望价格组合。然后可以根据ey与y的关系得到y。

下面对该算法的性能进行仿真。首先验证算法的收敛性。我们假设用户的感知成本服从均匀分布，图1展示了在服务器评估错误概率为0.1、N/M=0.1的条件下，定价误差绝对值和服务器平均收益随学习次数增加的性能变化情况：由于平均奖励值利用了历史标签数据，之前在当前价格上每次测试得到的用户感知精度都会反馈影响到当前价格的滑动方向，该算法收敛速度较快。由图1可以看到，达到稳定价格的学习次数与定价间隔数接近，而服务器的平均收益随着学习次数增加而增加，最终稳定在期望平均收益附近。

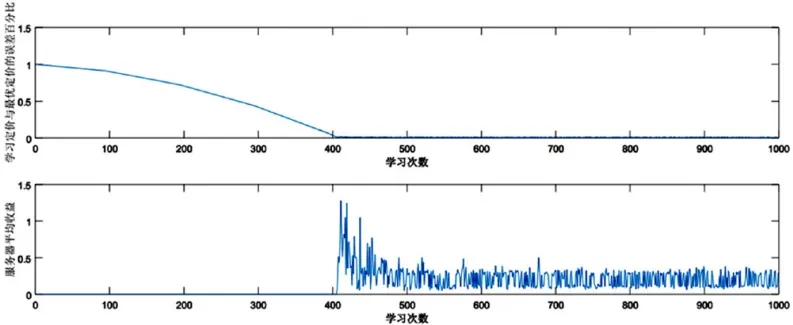
图1 感知成本服从均匀分布时SPA算法的性能

此外，我们还试验了用户的感知成本服从高斯分布的情况，算法的性能与均匀分布的情况十分类似，仿真结果如下图所示：

图2 感知成本服从高斯分布时SPA算法的性能

综合图1和图2可以看出，我们提出的滑动定价算法具有用户适应性、成本节约性和感知安全性。

5 结束语

本文提出了面向智慧城市应用的群智感知模式，即固定价值的多精度群智感知，并基于Stackelberg模型建立了定价收益模型。随后在完全博弈信息条件下，在考虑了服务器评估错误概率的基础上，得到激励用户选择某种精度感知的定价存在区间，并得到了使虚假感知最少和服务器收益最大化的最优定价。然后在感知成本位置的不完全信息条件下，基于Q学习设计了滑动定价算法SPA。随后通过仿真验证了算法的用户适应性、成本节约性和感知安全性。