油罐热变形有限元模拟研究
2019-11-11康习锋
郭 欣,康习锋,杜 欣
(中国人民警察大学,河北 廊坊 065000)
0 引言
油罐受热辐射发生变形不仅指宏观上的变形破坏,还包括罐壁材质受热后发生不可恢复的塑性变形。火灾环境下,邻近罐接收来自火焰的热辐射,油罐外壁温度迅速上升,热量通过热传导方式从外壁传导到内壁,罐壁在内外温度差的作用下会产生热应力,随着温度的增加,热应力逐渐增加,当热应力大于屈服强度后油罐失效发生塑性变形[1]。ANSYS软件可提供结构、流体、热、磁学等单元模块,也可进行多物理场耦合的计算分析。通过多物理场耦合分析,将一个场的分析结果作为另一个场的输入源,如热力耦合问题[2-3]。
火灾环境下的邻近油罐,受着火罐热辐射作用后,罐外壁温度迅速上升,在热传导作用下,罐壁内部温度场分布不均匀,导致罐壁内部的热应力不同。采用ANSYS软件进行邻近油罐热-结构耦合分析,应用多物理场间的耦合关系[4],通过非线性瞬态热分析,把求得的温度作为体载荷,分析罐壁的应力应变变化情况。
1 油罐热变形有限元分析
油罐热变形有限元分析分为热分析、结构分析和热-结构分析。
1.1 热分析
系统传热分为稳态传热和瞬态传热。通常可在计算瞬态热分析前,利用稳态热分析求解初始温度分布。当系统的净热流率为0,即系统自身产生的加上系统流入的热量等于系统流出的热量,系统处于稳态热[5]。稳态热条件可以表示为:
Qgene+Qin=Qout
(1)
其中,Qgene为系统自身产生的热量,J;Qin为系统流入热量,J;Qout为系统流出热量,J。
瞬态传热过程是指系统加热或冷却过程,在这个过程中,系统内能随着时间有明显变化[6]。ANSYS完成两部分的计算,第一部分是热学计算,完成瞬态传热计算;第二部分是结构力学计算,输入热学结果作为力施加载荷,完成油罐在温度载荷作用下的强度计算。瞬态热分析的热平衡表达式[7]如下所示:
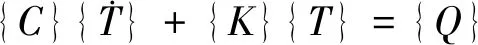
(2)
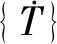
1.2 结构分析
结构分析是有限元分析方法中最常用的应用领域,火灾环境下罐壁采用的结构分析是静力分析。通过计算得到罐壁在热载荷作用下应力、应变和位移等参数的变化[8]。火灾环境下的油罐,在高温下由于罐壁强度和弹性模量的下降,造成油罐发生塑性变形和弹性变形。塑性变形指物体在外力的作用下产生形变,当外力撤除后物体不能恢复原状的现象。当材料发生塑性变形,应力与应变之间为非线性变化关系,大多数的金属可通过对比分析材料的屈服应力和等效应力的大小判断是否发生塑性变形[9]。Von Mises屈服准则是最常使用的屈服准则,塑性变形的发生取决于等效应力是否超过了材料屈服极限,其中等效应力可表示为[10]:
σe=
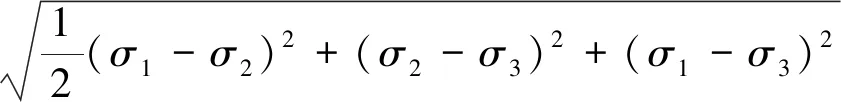
(3)
式中,σe是等效应力,σ1、σ2、σ3是三个主应力。
1.3 热-结构耦合分析
ANSYS 的多物理场耦合分析是对两个或两个以上物理场之间的相互作用的分析。火灾环境下邻近油罐罐壁受热辐射影响,罐壁的温度场分布不均匀,导致在结构场里产生热应力和热应变,同时高温也使油罐材质的物理性质发生变化,变化可用ANSYS热-结构耦合来分析[11]。油罐火灾热力耦合分析是通过载荷耦合法实现,即温度场和位移场之间的耦合,温度场的节点温度结果作为结构静力学场中的体载荷的施加,载荷通过体或表面,由多场求解器定义求解顺序,耦合载荷在不同的网格间自动传递,用于稳态和瞬态计算[12]。
2 油罐热变形有限元模拟
2.1 油罐材质基本属性
模拟的油罐材质为大型拱顶油罐常用材料SPV490Q钢,部分机械性能指标[13]见表1。
2.2 模型建立和网格划分
ANSYS 热分析涉及到的单元大约有40种[14],本文建立的油罐模型需要进行热-结构耦合分析,因此选择三维热分析单元solid70和surf152,主要用于实体的稳态或瞬态的热分析[15],能够对各种变化载荷和表面效应进行求解。本文研究罐壁材质的应力、应变与温度的关系,不受油罐尺寸的影响,只与油罐材质与厚度有关,模型只建立罐壁部分。选取圆柱体建模,并对底面进行约束,DOF=0,试样长度L=600 mm,外径R=1 000 mm,壁厚W=5 mm,选取正四面体网格划分,建模与网格划分如图1所示。

表1 SPV490Q钢的机械性能参数

图1 建模与网格划分
2.3 施加载荷
油罐变形的计算分两步,第一步施加温度载荷进行瞬态热分析,由于油罐在着火过程中内外存在温度差,因此内外壁施加不同温度载荷,计算材料在温度场作用下的温度分布;第二步转换单元类型,进行结构力学计算,将热分析计算的结果,即温度分布载荷作为结构力学的施加载荷计算热力耦合结果。加载求解中,罐壁的初始温度设定为20 ℃,取10个不同时间点对应的温度,以表变量的形式进行加载。温度载荷为40 ℃、60 ℃、80 ℃、100 ℃、150 ℃、200 ℃、250 ℃、300 ℃、400 ℃、500 ℃。同时设置分析类型为瞬态分析,加载时间设置500 s,时间步长取50。关闭时间积分,用默认的稀疏矩阵求解器进行求解。
3 模拟结果分析
3.1 罐壁应力分布趋势
模型一端约束施加不同温度热载荷,罐壁发生明显的应力集中现象,随着温度载荷的增大,罐壁最终发生失效变形。模拟求解后得到罐壁应力分布,其中,温度500 ℃时应力分布如图2所示。
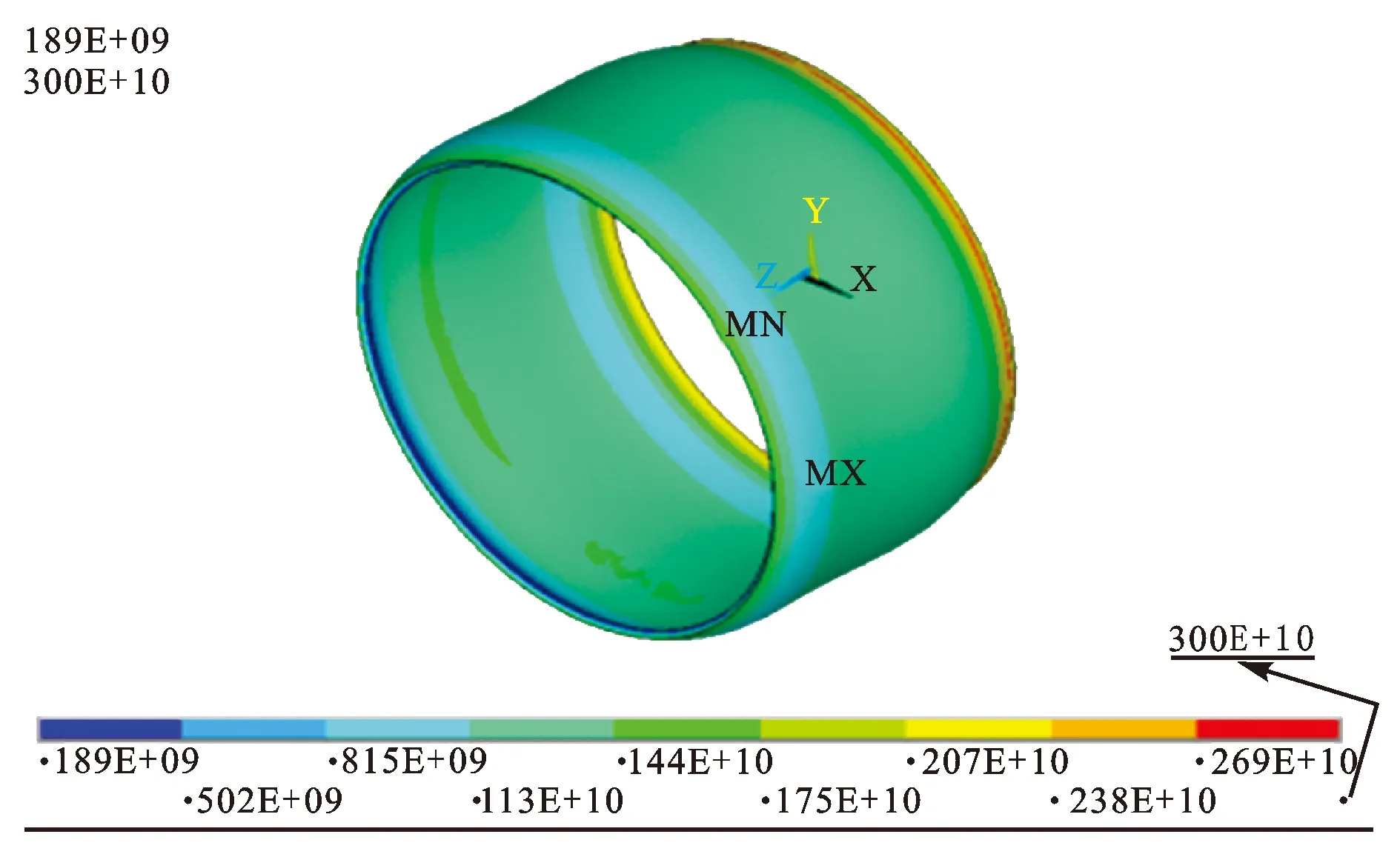
图2 500 ℃时罐壁应力分布图
模拟计算得到应力最大处的三向应力即轴向应力、环向应力、径向应力值随温度变化曲线如图3所示。
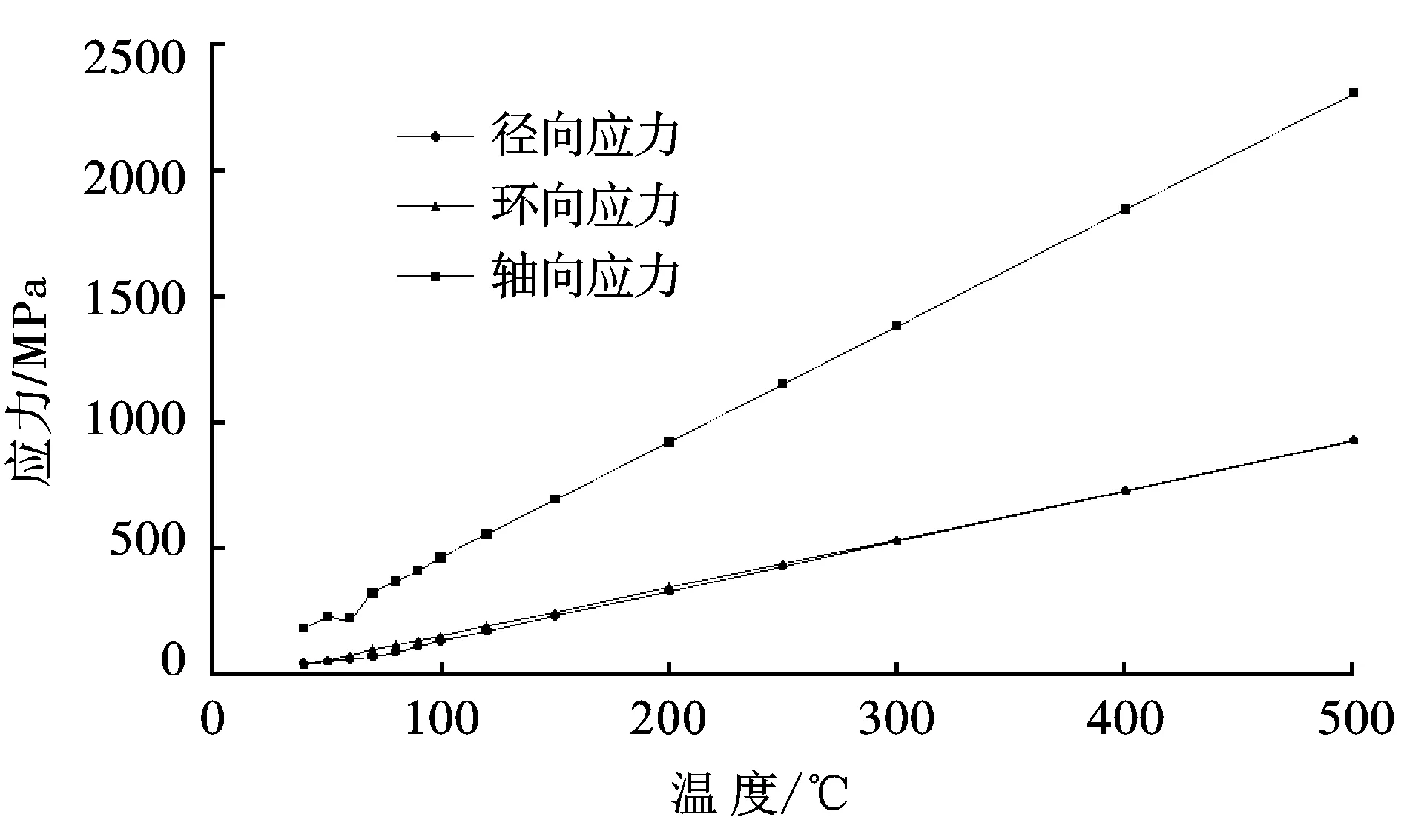
图3 不同温度三向应力值
如图3所示,三向应力随着温度的升高而逐渐升高,应力随温度呈线性增长趋势。同一温度作用下,轴向应力值增长最快,远大于环向和径向应力的增长速度,环向和径向应力随温度升高增长趋势和速度基本一致。说明材料在高温作用下,沿轴向的变形最大。
等效应力与温度拟合关系曲线图如图4所示。
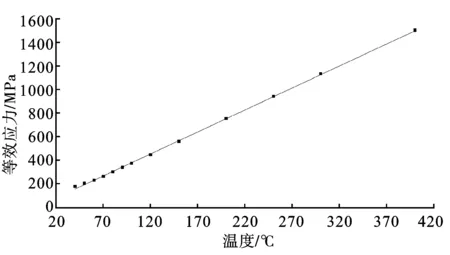
图4 等效应力与温度关系曲线
从图4可见,随着温度升高,罐壁的应力以近似线性方式增大。对温度变化的曲线进行拟合,得出等效应力随温度变化的函数σ=f(T),拟合函数式如式(4)所示:
σ=3.7259T+6.5038
(4)
式中,T为温度,℃;σ为应力,MPa。
R为拟合度,R2=0.999 6。
3.2 罐壁屈服强度
研究火灾环境下罐壁上的应力变化,应熟悉罐壁材料在不同温度下的力学性能随温度变化情况,这是研究罐壁受热应力变化的重要数据。高温作用时,金属罐壁材质的物理性能和力学性能会随温度升高发生变化,其中相关参数有热导率、密度、比热、屈服强度、弹性模量、泊松比和热对流系数等。在火灾环境下邻近油罐在热辐射的作用下会发生罐壁应力失效,失效机理是随着罐壁温度升高,罐壁材质的屈服强度不断降低,在热应力的作用下,当屈服强度低于所受应力时,罐壁会发生塑性变形而失效[16]。
欧洲钢结构协会(ECCS)根据大量的试验研究给出了钢的屈服强度随温度变化公式[17],如式(5)、(6)所示:
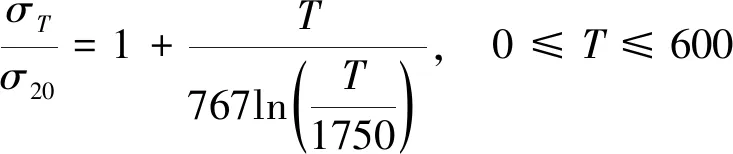
(5)
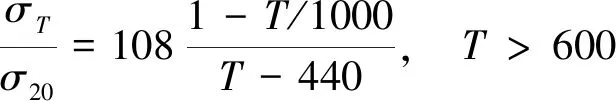
(6)
式中,σT为温度T时的罐壁材料屈服强度;σ20为温度20 ℃时的罐壁材料屈服强度;T为罐壁材料实时温度。
利用该公式计算SPV490Q钢在不同温度作用下的屈服强度,见表2。
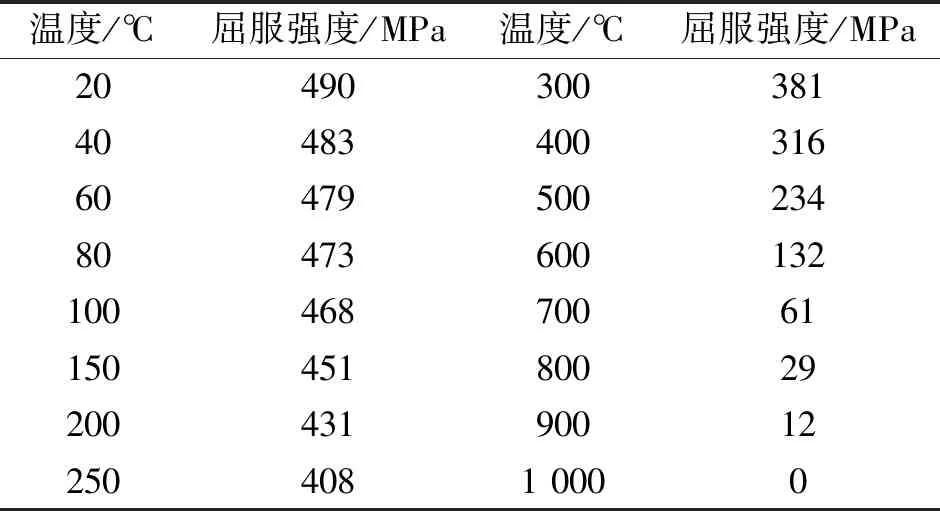
表2 SPV490Q钢不同温度下对应的屈服强度值
由表2得到SPV490Q钢屈服强度随温度变化曲线,如图5所示。
由表2和图5可见,随着温度的升高,SPV490Q的屈服强度逐渐下降,在200 ℃之前,下降趋势较缓慢。200 ℃后,材质的屈服强度迅速下降,到1 000 ℃时,公式计算材质的屈服强度接近为0。说明此材质罐壁在热辐射作用下,随着罐壁温度上升,屈服强度下降明显,当屈服强度低于所受应力时,罐壁发生变形。
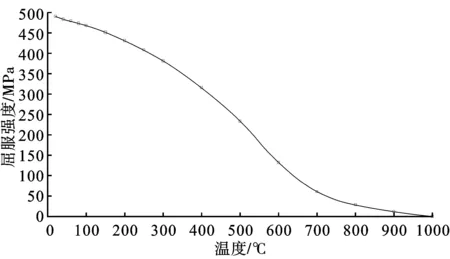
图5 屈服强度随温度变化趋势
3.3 罐壁屈服临界温度
由模拟得到不同温度载荷下,油罐应力值与屈服强度变化,见表3。
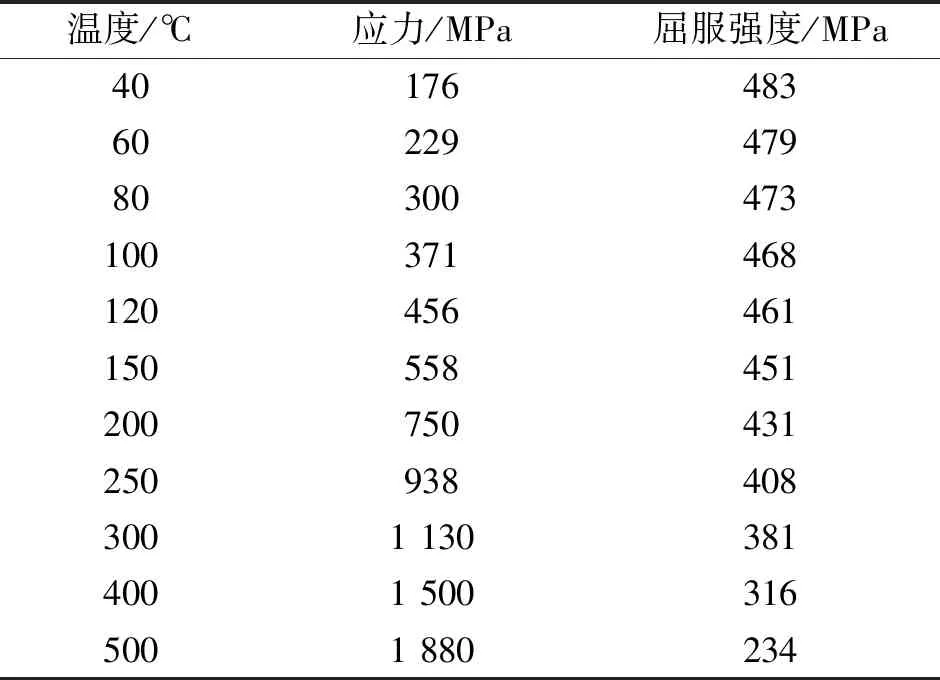
表3 应力与屈服强度
罐壁屈服强度与等效应力值随温度变化曲线如图6所示。
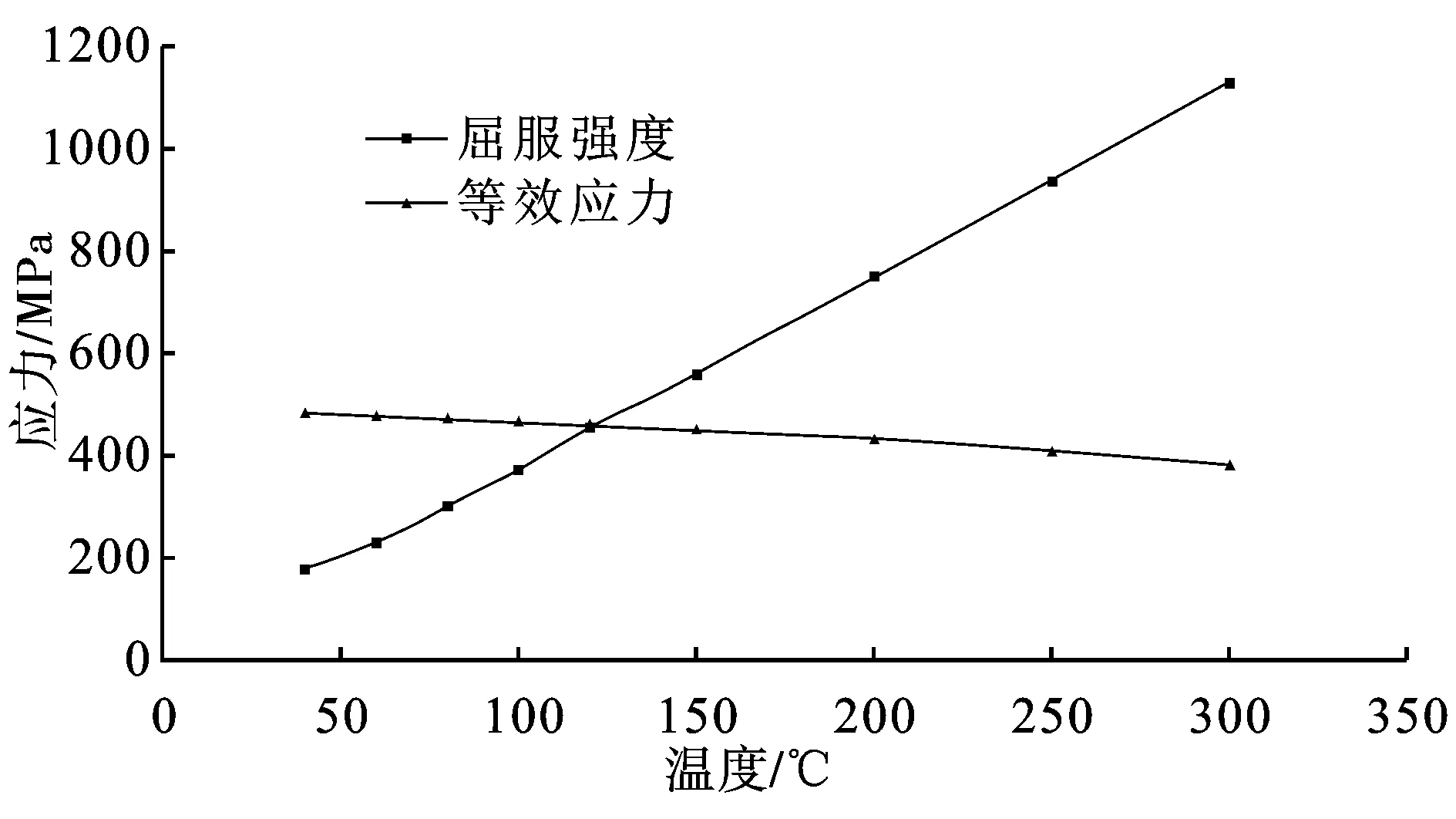
图6 油罐屈服强度与等效应力值
由图6可见,温度升高,罐壁应力逐渐增大,屈服强度逐渐下降。将仿真计算的结果与公式计算所得的屈服强度进行对比,两条曲线相交的点是屈服强度与总应力值相等的点,罐壁温度120 ℃时,总应力为456 MPa,接近材料的屈服强度461 MPa,当温度低于120 ℃时,应力值小于屈服强度值,罐壁强度满足安全要求。当温度超过120 ℃后,材料的应力继续增大,屈服强度继续下降,应力值开始超出屈服强度值,罐壁因为结构强度不足而发生屈服破坏。因此120 ℃可以认为是该材料发生塑性变形的临界温度。
4 结论
根据邻近油罐罐壁表面的热辐射强度分布特点,借助有限元分析软件,模拟火灾场景下油罐罐壁应力随温度的变化规律,得到如下结论:
4.1 通过对不同内外壁温差作用下的罐壁瞬态热力学分析获得了罐壁应力随温度升高的变化特点:三向应力均接近线性趋势增加,其中轴向值最大。由温度和应力变化趋势图得到罐壁应力与温度的关系模型σ=3.7259T+6.5038。
4.2 分析SPV490Q钢随温度升高应力值和屈服强度的变化,得到罐壁屈服的临界温度:当温度达到120 ℃时,其总应力已接近屈服强度,因此120 ℃可作为该材质产生塑性变形的临界温度。
