层厚比对钛/铝复合板拉伸力学性能的影响

黄华贵，刘禹彤，孙静娜，季 策

(1.燕山大学 国家冷轧板带装备及工艺工程技术研究中心，河北 秦皇岛 066004；2.燕山大学 机械工程学院，河北 秦皇岛 066004)

0 引言

钛/铝层状复合板兼具钛良好的耐腐蚀、耐高温、抗冲击韧性、生物兼容性高和铝轻质、高导热性等优点，通过“以铝节钛”降低钛用量，大大降低使用成本，在航空航天、高端厨具等领域具有广泛的应用前景。然而，两种组元材料显著的力学性能差异，使复合板在制备和后续深加工中变形协调性问题难以解决，往往造成加工工艺复杂化[1-3]。为解决复合材料的制备问题，国内外学者相继提出了爆炸复合[4]、轧制复合[5-6]、固-液铸轧复合[7-10]等工艺，并围绕其界面微观组织和宏观力学性能等方面开展了大量研究工作。在复合板力学性能研究方面，关凌云[11]通过测定不同金属复合板中基材及复材纯组元材料的拉伸性能、剪切性能及显微硬度，建立了金属复合板界面剪切强度与纯组元材料性能之间的关系式。Lee等[12]对钛/铝复合板进行了拉伸试验和维氏硬度测试试验，提出了用屈服应力与硬度的关系求应力-应变曲线的数值方法，并将其应用到有限元分析中。徐卫等[13]对钛/铝复合板进行等温拉伸实验，发现钛/铝复合板在单向拉伸时，岀现翘曲现象，且伸长率随变形速率的增大而增大。赵军[14]等用解析法推导复合板塑性失稳的公式，研究了失稳点与复合比的关系。刘洪伟等[15]建立了宽度方向应力与相对厚度比和拉伸应变之间的关系，研究发现试样宽度方向应力与厚度比有关。夏琴香等[16]研究各工艺参数对复合板拉深成形工艺的影响。Motarjemi等[17]利用传统混合法则，预测了钢/铝复合板力学性能。研究结果表明，虽然复合板力学性能与制备过程中诸多工艺参数有关，但在最终服役或使用时，主要取决于终态下的组元金属自身力学性能和组元层厚比。

作为新型结构和功能一体化材料，钛/铝复合板在充分发挥其功能化特性基础上应尽量减少钛的用量，而通过改变层厚比实现复合板综合力学性能的合理设计，可以满足不同领域需要。因此，研究层厚比对钛/铝复合板拉伸力学性能的影响规律具有重要的理论与实际意义。本文通过实验法获得组元金属力学性能及复合板的力学性能，用ABAQUS软件建立不同层厚比的钛/铝复合板单向拉伸过程模型，探究钛/铝复合板的层厚比对力学性能的影响。

1 复合板及组元材料单向拉伸实验

1.1 拉伸试件制备

拉伸实验材料选用不同层厚比的钛/铝复合板，结合生产中常用规格，所用钛/铝复合板厚度与层厚比参数如表1所示。钛板牌号为TA1，铝板为3003铝合金，参照标准《金属材料 室温拉伸试验方法 GB/T 228—2002》制备试件。为了获得组元材料的性能参数，需要对组元材料分别进行单向拉伸实验，但由于钛/铝复合板中钛层厚度只有0.5 mm左右，难以通过机械加工分离复合板，因此，本文通过线切割按图1尺寸获取复合板试件，用砂纸打磨切割边界，去毛刺。首先对钛层铣削获取铝侧拉伸试件，再根据强碱溶液与铝反应而不与钛反应的性质，将复合板放入NaOH溶液中进行化学反应得到钛侧拉伸试样，组元材料试件如图2所示。

表1 钛/铝复合板厚度与层厚比参数

Tab.1 Parameters of thickness and thickness ratio of Ti/Al clad plate

序号总厚度mm钛层厚度mm铝层厚度mm钛层占比α%试件#12.4802.480试件#23.180.482.715.1试件#32.8670.52.36717.4试件#42.9250.5592.36619.1试件#52.3650.571.79524试件#62.10.5451.55526试件#70.5150.5150100

图1 拉伸试件尺寸

Fig.1 Tensile specimen size

图2 组元材料拉伸试样

Fig.2 Component material tensile specimen

1.2 实验结果

在INSPEKT TABLE100电子万能试验机上进行单向拉伸实验，拉伸速率为2 mm/min，为更加准确地测量应变得到准确的弹性模量与屈服强度，实验中夹装MFA 25应变式电子引伸计，标距为25 mm，得到表2为组元金属钛和铝的基本力学性能参数。

表2 钛和铝的基本力学性能参数

Tab.2 Basic mechanical properties of titanium and aluminum

材料E/GPaRm/MPaRp0.2/MPaTA1100492.36452.32300353.32112.12103.96

由单向拉伸实验得到图3为钛层占比α不同时钛/铝复合板及组元材料钛和铝的应变-应力曲线，从图中可以看出，各层厚比下钛/铝复合板的强度、均匀伸长率、断裂伸长率等力学性能均介于组元材料钛和铝之间。

图3 不同层厚比的钛/铝复合板及组元材料的拉伸应力-应变曲线

Fig.3 Tensile stress-strain curves of Ti/Al clad plates and component materials with different thickness ratios

1.3 复合板拉伸断裂分析

拉伸变形过程中，一方面随着试样长度增加，根据塑性变形体积不变定律，横截面积均匀减少使材料的承载能力降低，另一方面变形产生的加工硬化使变形抗力提高，阻碍变形区进一步变形，使变形区不断转移，促进变形的均匀扩展。从屈服到颈缩的阶段是稳定的塑性变形阶段，在这一阶段，材料加工硬化的作用超过试件横截面积均匀减少的作用，应力随应变的增加而提高。加工硬化是由于位错的积累阻碍了其他位错的通道，拉伸过程中位错的湮灭、重新排列、交叉滑移都会降低加工硬化的程度，当加工硬化的作用与面积减小的作用相等后，最弱的截面处承载能力得不到提高，变形开始集中，形成颈缩，应力随应变的增加而不断减小，直至试件断裂，拉伸断裂形貌如图4所示。

图4 钛/铝复合板拉伸断裂形貌

Fig.4 Tensile fracture morphology of Ti/Al clad plate

由于钛的硬化指数较小，稳定均匀塑性变形的能力较差，当复合板的拉伸变形量达到钛的均匀伸长率时，钛先出现颈缩趋势，但由于铝的均匀塑性变形的能力较强，且复合板结合性能较好，所以钛的颈缩和铝均匀变形相互抑制，导致复合板的均匀伸长率介于两种材料之间。

在断裂分离阶段，由图3可知由于钛的韧性比铝好的多，颈缩变形能力强，间接提高了铝的颈缩变形能力，使铝在达到断裂应变后能同钛继续共同变形。由于钛与铝的泊松比、塑性应变比等性能的差异，拉伸过程中钛侧在宽度方向的缩短大于铝侧，而界面的约束使试件在宽度方向出现附加应力，复合板拉伸试件产生图4(b)的向钛侧翘曲的现象。

同时，在拉伸过程中界面未出现明显的分层现象，断裂曲线平滑未出现阶梯，说明复合板界面结合良好。

2 弹塑性有限元模拟

2.1 单向拉伸模型的建立

利用ABAQUS软件建立三维实体模型对钛/铝复合板的单向拉伸过程进行弹塑性分析，由拉伸实验可知，复合板界面实现冶金结合，结合良好，建模时不考虑界面层对复合板的影响，将模型按层厚比分割为基体和覆层两部分，分别赋予表2的组元材料参数，在钛/铝复合板拉伸的弹塑性分析中，钛、铝层材料均采用Mises屈服准则，等向硬化模型，输入实验得到的钛和铝的真应力-塑性应变数值插值拟合塑性参数，如图5所示。设置网格为C3D8R六面体实体单元，将两夹持端约束为刚体，一端固定，一端以2 mm/min匀速加载，如图6所示。根据单变量分析原则，模拟中复合板总厚为2 mm、2.5 mm、3 mm，钛层厚度分别为0.3 mm、0.4 mm、0.5 mm、0.6 mm。

图5 TA1和3003的真应力-塑性应变曲线

Fig.5 True stress-plastic strain curves of TA1 and 3003

图6 单向拉伸模型图及边界条件

Fig.6 Tensile finite element model and boundary conditions

2.2 模型的验证

参照表1的板料规格在相同实验条件下做单向拉伸模拟，图7为17.4%层厚比复合板实验与模拟的载荷位移曲线对比，由图可知实验与模拟曲线的吻合程度较高，可用于层厚比对拉伸力学性能影响的研究。

图7 17.4%层厚比的复合板实验与模拟对比

Fig.7 Comparison between experiment and simulation of composite plate with 17.4% thickness ratio

2.3 模拟结果

由于模型只考虑均匀塑性阶段，因此只模拟到复合板颈缩，典型模拟结果如图8所示，根据模拟结果中不同层厚比时的复合板拉伸载荷位移曲线，计算得到应力应变曲线，结果表明复合板的拉伸力学性能介于两种组元材料之间，利用ORIGIN软件拟合模拟数据，分别分析抗拉强度、屈服强度、弹性模量与层厚比的关系。

图8 颈缩变形图

Fig.8 Necking deformation diagram

图9是不同层厚比时复合板的抗拉强度，线性拟合的公式为

y=3.802 35x+111.801 06，

拟合度因子为0.999 99。图10是不同层厚比时复合板的屈服强度，线性拟合的公式为

y=3.144 59x+102.694 81，

拟合度因子为0.999 74，图11是不同层厚比时复合板的弹性模量，线性拟合的公式为

y=0.488 54x+51.306 11，

拟合度因子为0.999 98。

图9 不同层厚比的抗拉强度

Fig.9 Tensile strength of different thickness ratio

由拟合结果可知抗拉强度、屈服强度、弹性模量均与组元材料性能和层厚比呈明显的线性关系，拟合公式基本符合层厚比加权平均规律[18],

σm=σma·α+σmb·(1-α)，

(1)

σp0.2=σp0.2a·α+σp0.2b·(1-α)，

(2)

E=Ea·α+Eb·(1-α)，

(3)

式中，σm为复合板抗拉强度，MPa；σma为覆层金属抗拉强度，MPa；σmb为基板金属抗拉强度，MPa；σp0.2为复合板屈服强度，MPa；σp0.2a为覆层金属抗拉强度，MPa；σp0.2b为基板金属抗拉强度，MPa；E为复合板弹性模量，MPa；Ea为覆层金属弹性模量，MPa；Eb为基板金属弹性模量，MPa；α为层厚比，%。

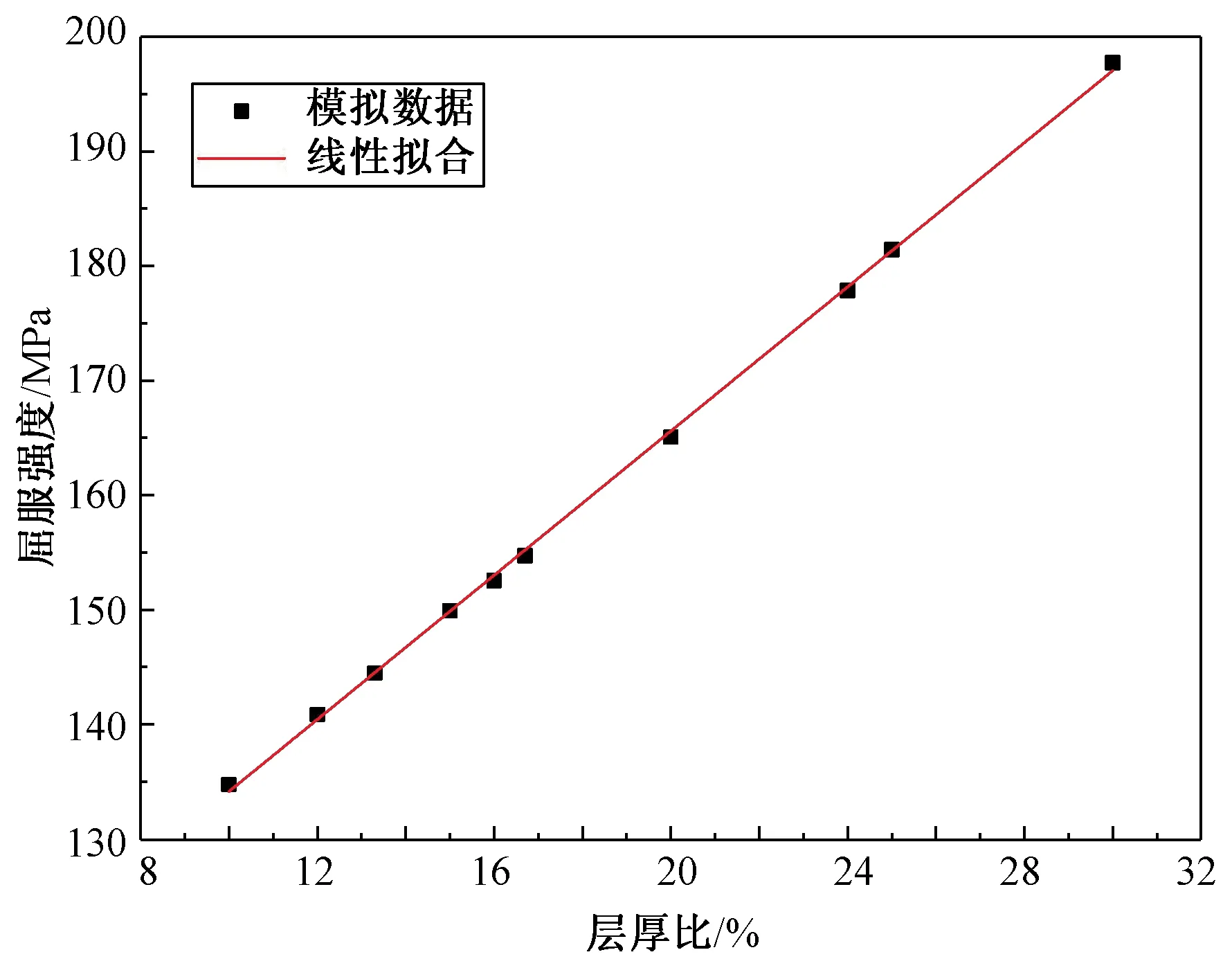
图10 不同层厚比的屈服强度

Fig.10 Yield strength of different thickness ratio

图11 不同层厚比的弹性模量

Fig.11 Elastic modulus of different thickness ratio

2.4 对比分析

结合实际复合板拉伸实验数据、层厚比加权平均规律与有限元模拟数据，对比不同层厚比的钛/铝复合板的拉伸力学性能，如图12～14所示。

由图12可知，抗拉强度的实测值、加权公式计算值与模拟值的相对误差在+0.15%～+0.7%之间，吻合程度高，验证了有限元模拟和加权公式预测复合板抗拉强度的准确性。

图12 抗拉强度的拉伸实验实测、模拟与加权公式对比

Fig.12 Comparison of measured, simulated and weighted calculation values of tensile strength

图13 屈服强度的拉伸实验实测、模拟与加权公式对比

Fig.13 Comparison of measured, simulated and weighted calculation values of yield strength

由图13可知，屈服强度的加权公式计算值和实测值均略大于模拟值，实测值、加权公式计算值与模拟值的相对误差在-0.15%～+6.73%之间，吻合程度较高，验证了有限元模拟和加权公式预测复合板屈服强度的准确性。

由图14可知，弹性模量的实测值、加权公式计算值与模拟值吻合良好，相对误差在-5.9%～+7.14%之间，验证了有限元模拟和加权公式预测复合板弹性模量的准确性。

图14 弹性模量的拉伸实验实测、模拟与加权公式对比

Fig.14 Comparison of measured, simulated and weighted calculation values of Elastic Modulus

3 结论

1)分析钛/铝复合板断裂机理，发现钛侧先出现颈缩与断裂趋势，复合板的强度、均匀伸长率、断裂伸长率等力学性能介于两种组元材料之间。钛侧在宽度方向的变形大于铝侧，界面的约束使试件在宽度方向出现附加应力，导致复合板拉伸试件产生向钛侧翘曲的现象。在拉伸过程中界面未出现明显的分层现象，断裂曲线平滑未出现阶梯，说明复合板界面结合良好。

2)用ABAQUS建立了钛/铝复合板单向拉伸过程的弹塑性模型，分析其力学性能与层厚比的关系，结果表明钛/铝复合板的抗拉强度、屈服强度与弹性模量基本符合层厚比加权平均规律，上述方法可用于预测复合板的力学性能参数，并为实现复合板综合力学性能定量化设计奠定了基础。