永磁三自由度电机的磁场分析与电磁计算
2019-11-11刘令旗
李 争,刘令旗,杨 凯
(河北科技大学 电气工程学院,河北 石家庄 050018)
0 引言
一个复杂繁琐的多体机械系统中,往往伴随着非线性、强耦合的控制方法与多样式、多自由度的运动工况[1-3]。单一多台传统电机相互配合构成的传动装置,一来系统体积重量过于庞大,而且多个轴承的相互间隙容易影响传动装置的旋转精度;二来对于规划复杂的多自由运动,也有响应速度较慢、传动灵活性差的缺陷[4-7]。为此,国内外学者为解决上述存在的局限性,纷纷致力于具有多个旋转自由度特种电机的设计和研究[8-10]。多自由度电机具有体积轻巧、结构紧凑、材料利用率和机械集成度较高的诸多优势,从而大幅度地减少了系统耦联机构的数量,同时也使电机定位运动的精度得以进一步提高。随着电机磁场对性能指标要求的不断提升,Halbach阵列的永磁体结构受到人们广泛关注和应用。相比常规单向充磁的永磁电机,其磁化方向分别沿径向与切向、依据角度连续变化的组合而成,通常介于制作工艺的考虑,将永磁体分级分块后,使任一相邻磁体的夹角保持一致,营造出一侧聚磁一侧屏蔽的单边效应,可获得更为正弦的气隙磁场与更小的转矩波动[11-13]。传统的多自由度电机采用相同的绕组控制进行旋转和偏转运动,致使自转速变慢,偏转运动不能达到高精度。因此,本文提出了一种新型永磁混合驱动三自由度电动机。该电机的三自由度运动由外部旋转模块和内部偏转模块完成[14-16]。依据该多自由度电机的结构特性与工作原理,首先对电机自转模块在不同充磁方式下的涡流损耗与铁芯损耗加以论述和研究,再分别基于电机自转模块与偏转模块的静态磁场特性进行分析,得到了更为均匀的磁力线分布和更为正弦的气隙波形;在瞬态磁场下,对电机自转模块的瞬态特性进行有限元计算,得到了较为理想的自转转矩曲线;同样对电机自转模块的瞬态特性进行有限元计算,并在逐次通电后求解得到了合理的倾斜范围[17]。
1 混合驱动式电机的电磁损耗分析
所提出的永磁三自由度电机的驱动机理为混合驱动式,包含两种类型的电动模块,一类为自转型的电动模块,另一类为偏转型的电动模块。电机可在对应的模块中,依据各自的铰链约束,独立完成自转与偏转运行,完成电机的倾斜操作和旋转运行,也可在两种不同控制策略的协同控制的配合下,实现空间内的三自由度同步运转。当电机实现自转运动时,由自转定子线圈通电后与自转永磁磁场相互作用,联动与电机外壳相接的对外输出轴,电机实现偏转运动时,由偏转定子线圈通电后产生极性相反的磁场,与偏转永磁体“同斥异吸”,同时带动整个电机的自转模块,且偏转模块中的转子轭同时为自转模块中的定子轭。图1为电机的整体结构示意图,图2为电机的剖面结构示意图。表1为电机的结构参数表。

图1 电机整体示意图
Fig.1 Overall motor schematic

图2 电机截面示意图
Fig.2 Schematic diagram of the motor
在电机的外围自转模块的定子绕组通以三相工频交流电,转子磁轭在处于强度不等、方位互异的变化磁场中时,会产生涡流效应,而电机的内、外转子部分涡流损耗的主要因素是磁场空间、电流时间和绕组反电动势的谐波分量,但由于混合驱动式永磁电机选取两组不同的激励线圈,均以内侧定子、外侧转子形式将自转、偏转永磁体包络封装于转子磁轭内,而当电机内外转子协同控制时,此时作用于自转、偏转模块内的永磁体一律视为内置式结构,因而其散热条件较差。电机做空间三自由度运动时容易引发自转、偏转模块内永磁体的局部发热,这会导致永磁体的磁性能有所衰减,甚至造成整体产生不可逆退磁风险的增加,同时内、外转子部分也会在切割磁力线时产生感应电动势和电流。感应电流流经定子铁芯产生铁芯损耗,以及电机定子绕组通电发热后产生的铜损耗。这都成为电机运行可靠性及使用寿命中不可忽视的因素。
表1 电机结构参数
Tab.1 Parameters of motor structure

参数 参数值 自转定子外径/mm105 偏转定子内径/mm52 自转转子外径/mm120 偏转转子内径/mm70 内、外气隙/mm3 自转定子齿极数Ns12 自转转子齿极数Nr8 自转定子轭高/mm90 偏转定子轭高/mm75 转子轭高/mm135
1.1 内、外转子永磁体涡流损耗的解析法
依据法拉第电磁感应定律,电机在自转和偏转同步推进时,偏转永磁体、磁轭和支撑连杆在内部做连续俯仰、偏航的运动,从而切割自转模块内的磁力线;自转永磁体、磁轭在外侧高速旋转时,切割偏转模块的磁力线,进而分别产生对应感应电动势作用于对应模块的永磁体,并以导电介质为闭合回路形成感应电流,视为涡流现象。在永磁体内流通的感应电流所产生的电磁能量,其中绝大部分并未随转子轴运动以机械能形式输出,而是耗损在永磁体内部,致使其温度升高。在双绕组通电的协同控制下,转子永磁体在自转、偏转磁场内的三自由度运动所产生的感应电动势emn、贯穿永磁体N、S极的气隙磁通密度φmn以及谐波分量的极距τmn分别为
emn=ωmnφmn,
(1)
φmn=1/πBmnτmnhPM,
(2)
τmn=τr/[2p(m+n)],
(3)
式中,τr为初始永磁体时的极距,hPM是任一径向充磁永磁体分块分级的磁化方向的位移量。
在涡流场中感应电流的密度We可表示为
(4)
式中,σ为径向充磁永磁体的导电率,demn为相邻节点间感应电动势的波动值,dL为相邻节点间的长度。
将电磁场中的m×n次谐波作用于永磁体内部的瞬态磁通密度以Fourier级数分解如下:
(5)
所以,径向充磁永磁体的涡流损耗密度即为
(6)
将上述单个径向充磁永磁体进行积分:


(7)
再通过线性叠加后所得内、外转子永磁体的全部涡流损耗为
(8)
1.2 内、外定子磁轭铁耗的解析法
定子部分磁轭内的损耗囊括了涡流损耗Peddy、磁滞损耗Phys和异常损耗Pab,其中异常损耗为工程上考虑铁耗可能出现的附加量。其公式如下所示:
PFe=Peddy+Phys+Pab,
(9)
以单位质量表征异常损耗值Pab为
(10)
由于集中式定子绕组与磁轭的磁化方式不同,在基于其产生的旋转、交变磁场作用相互独立下,分别计算相应部分的损耗,采用将磁通密度的纵向和切向分离,继续求解如下两种损耗:
(11)
(12)
式中,G、V0为硅钢片的材料系数,S是其截面积,Br(t)、Bt(t)为磁通密度的横向和纵向分量。
经简化后,三自由度电机内、外定子轭总的铁芯损耗值可表示为
(13)
式中,kc、ke是涡流损耗和异常损耗的系数值。
1.3 电机涡流损耗、铁芯损耗的有限元法计算
图3和图4为驱动电机自转模块的一对N、S极永磁体的不同充磁方式对比,显然,相比永磁体平行充磁,径向充磁的永磁体在相同时段内的磁通密度略大,磁力线围绕环状永磁体的分布更为均匀。

图3 平行充磁下的磁密矢量
Fig.3 Magnetic density vector under parallel magnetization

图4 径向充磁下的磁密矢量
Fig.4 Magnetic density vector under radial magnetization
如图5和图6所示,电机的永磁体涡流损耗和定子磁轭铁芯损耗,取电机平稳运行阶段的1秒时长,分别对比在自转、偏转模块中永磁体在不同充磁方式下的损耗曲线,不难看出,基于两种不同充磁方式的角度差异,径向充磁的损耗曲线的相位角相比平行充磁的损耗曲线超前90°,平行充磁的永磁体涡流损耗为4.8 W左右,相比径向充磁时的4.5 W稍大,而二者铁芯损耗的曲线幅值大致相等,约为60 W,但平行充磁的损耗曲线图相较径向充磁的正弦趋势较差。
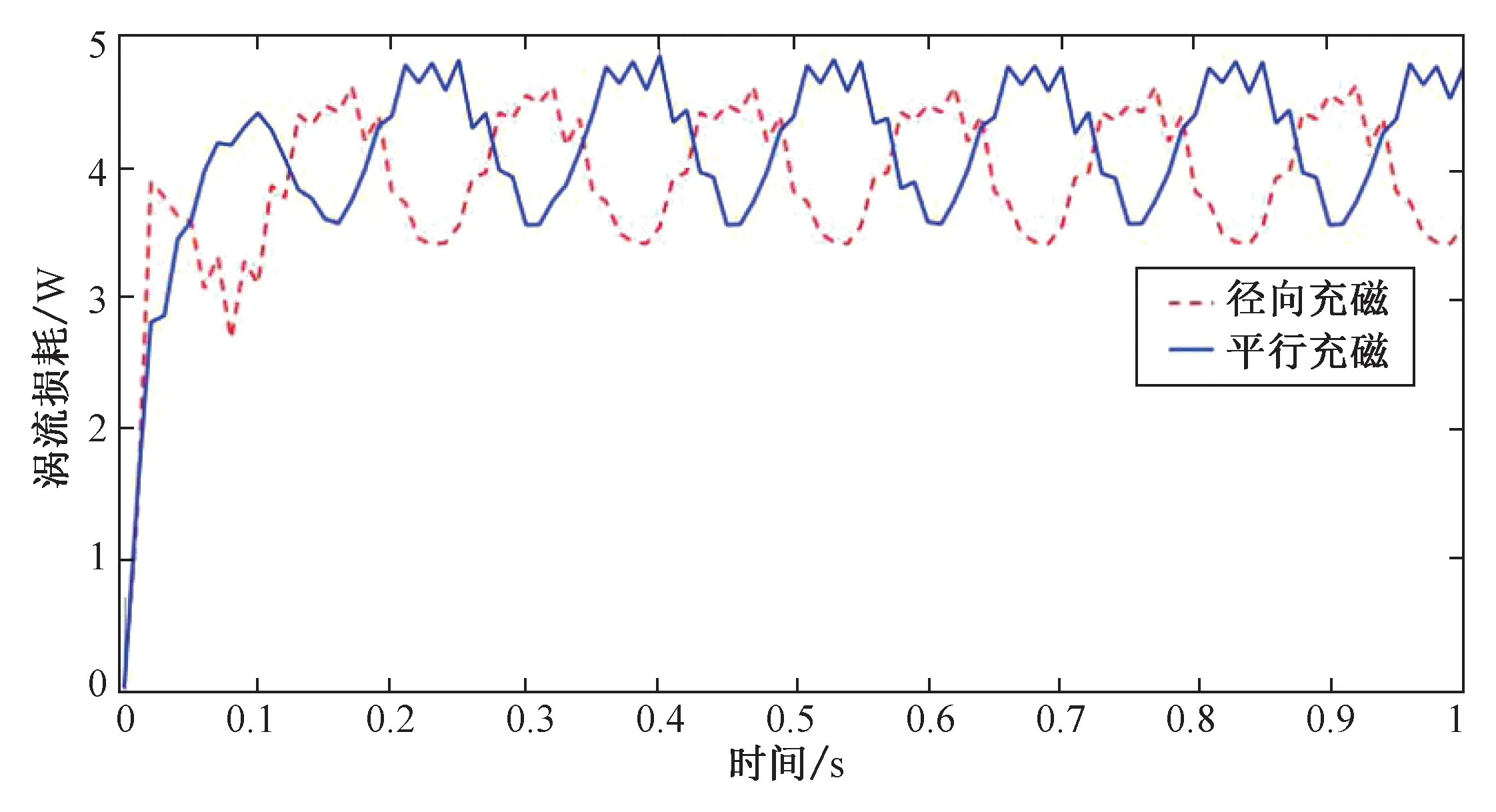
图5 不同充磁方式下的永磁体涡流损耗
Fig.5 Permanent magnet eddy current loss in different magnetization modes

图6 不同充磁方式下的铁芯损耗
Fig.6 Core loss in different magnetization modes
2 永磁三自由度电机的静态磁场分析
以永磁体磁通密度B为求解域下的目标函数,建立描述磁场分布与电流关系的麦克斯韦方程组

(14)
将永磁体气隙磁通密度分解为笛卡尔坐标系下的3个分量,并与表征3个方向的单位向量相乘后再相加,可表示为
B(x,y,z)=Bx·x+By·y+Bz·z。
(15)
提取偏转电机与自转电机中气隙磁密的分量,经过坐标转换后,分别映射至对应两类驱动模块下的柱坐标系与球坐标系,并于静磁场下进行求解和计算
B1θ=(Bxcosφ+Bysinφ)cosθ-Bzsinθ,
(16)
B2r=Bxcosθ+Bysinθ,
(17)
其中,B1θ(t)为球坐标系下气隙磁场的切向分量。B2r(t)为柱坐标系下气隙磁场的径向分量。
该多自由度电机的控制机理为混合驱动式,控制电机自转运动与偏转运动的模块中各有一组永磁体作为激励源,在空间与时间上的磁场分布得相对复杂,且自转永磁体为环状排列的四级八块式结构。由于相邻永磁体的间隙很小,会造成相互之间的谐波干扰,致使气隙磁通密度的幅值与正弦性有所下降。为获得更好的磁场正弦特性,并实现对内部偏转电机的零磁干扰。控制自转运动的永磁体采用柱坐标系下理想型的Halbach阵列充磁方式,即转子永磁体垂直方向上的磁化方式为整体无间隙的Halbach阵列排布,可将自转永磁体视为一个不可分割的磁环。在径向分量与周向分量上分别使用正、余弦变化的充磁方式,可实现环式结构永磁体对内环的强力聚磁效果与对外环天然磁屏蔽能力。
外围自转电机永磁体在理想Halbach阵列充磁下的磁力线分布与磁密矢量分布如图7和图8所示,可明显观测到自转模块于内侧聚磁、外围屏蔽的效果,且永磁体矢量磁密由S极流出指向N极,再由N极流出指向S极,在其内部形成8个闭合回路,符合自转永磁体的八极式结构,佐证了自转电机模型设计的合理性与可行性。磁力线位于永磁体环式磁路中,其走向趋势可更为集中地体现,相比径向充磁下的永磁体分布规律也更为均匀。

图7 理想Halbach阵列充磁下自转永磁体的磁力线
Fig.7 Magnetic lines of rotating permanent magnet under ideal Halbach array magnetization
而控制偏转操作的永磁体则为球形贴片式,在平行于电机内侧轴承的圆周上,依据间隔90°的顺序依次排布,仅在铅直方向上下分布的N、S极留有一定间隙,而相邻两块永磁体的气隙间距很大,不会导致谐波分量的干扰,因而采用球坐标系下的径向充磁方式即可。图9与图10分为偏转永磁体磁力线分布图与矢量磁密,其磁化方向沿半径指向球心,磁密矢量分布均匀。显然,N-S极交界面的磁力线分布最多,磁场最强;而每级中心线对应的截面上磁力线分布最为稀疏,磁场最弱。

图8 理想Halbach阵列充磁下自转永磁体的矢量磁密
Fig.8 Vector magnetic density of rotating permanent magnet under ideal Halbach array magnetization

图9 偏转永磁体的磁力线分布
Fig.9 Magnetic flux distribution of deflection permanent magnet
图11为偏转永磁体内侧气隙磁场的整体分布,显然,在球坐标系下定、转子之间的气隙磁场是沿空间角φ、θ有规律地排列。气隙磁密在θ方向上呈周期性分布,在俯仰角φ从0到360°的变化区间内,位于φ=kπ/2处,有4个波峰和4个波谷,共有8个极值点,峰值约为0.3 T。在方位角θ从-15°到15°的变化区间内,呈正弦趋势分布,变化周期为30°。
依靠沿球面方向的切向电磁力,混合驱动式电机可单独实现偏转运动。如图12所示为偏转永磁体内侧气隙磁场的径向分量分布,切向磁密于θ方向上同样呈正弦周期性变化。基于气隙磁场的切向分量Bφ随φ角矢量方向的正负变化,以φ= 90°、180°、270°、360°为中心的4点处,两侧分别出现两个对称的波峰和波谷,共有16个极值点。相比气隙磁密更为尖锐,峰值略小,约为0.2 T。在方位角θ从-15°到15°的变化区间内,切向磁场对应单个周期的变化呈现相反的正弦趋势,其合成分量随|θ-π/2|的变化而变化。在θ=π/2时为0。

图10 偏转永磁体的矢量磁密
Fig.10 Vector magnetic density of deflection permanent magnet

图11 偏转永磁体气隙磁场的整体分布
Fig.11 The overall distribution of the air gap magnetic field of the deflection permanent magnet
图13为基于Halbach阵列自转永磁体内侧气隙磁场,在柱坐标系下定、转子之间的气隙磁场随方位角θ、高度h的变化而变化。方位角变化的区间范围同样为旋转一周的0~360°,位于φ=kπ/2处,有4个波峰和4个波谷,对应的峰值为0.25 T,永磁体的高度为52 mm,对应垂直于z轴的上下范围为±26 mm,沿高度h方向则并无明显变化。
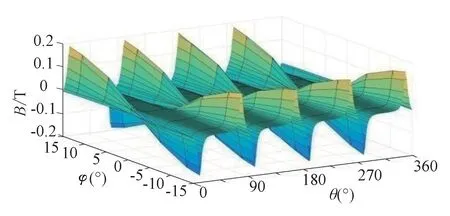
图12 偏转永磁体气隙磁场的切向分布
Fig.12 Tangential distribution of the air gap magnetic field of the deflection permanent magnet

图13 自转永磁体气隙磁场的整体分布
Fig.13 Overall distribution of the air gap magnetic field of the rotating permanent magnet
依靠沿转轴方向的径向电磁力,混合驱动式电机可单独实现自转运动。图14为基于Halbach阵列自转永磁体内侧气隙磁场的径向分布,与气隙磁场的变化趋势大致相同,谐波分量较小。沿周向呈正弦趋势变化,沿切向无明显趋势变化。

图14 自转永磁体气隙磁场的径向分布
Fig.14 Radial distribution of the air gap magnetic field of a rotating permanent magnet
3 永磁三自由度电机的瞬态磁场分析
对电机的自转模块通以三相工频交流电,指定自转转子初始电角度与电机运动的机械角度相匹配,使电机于初始时刻的感应磁势保持最大值,运行至仿真时长的一半时,图15与图16为自转模块瞬态的磁密云图与磁密矢量图。定子轭铁芯处磁场较强,气隙磁场相比于定子轭处较弱,磁场分布均匀,证明了电机模型和通电策略的合理性。

图15 自转模块的瞬态磁密云图
Fig.15 Transient magnetic dense cloud diagram of the rotation module
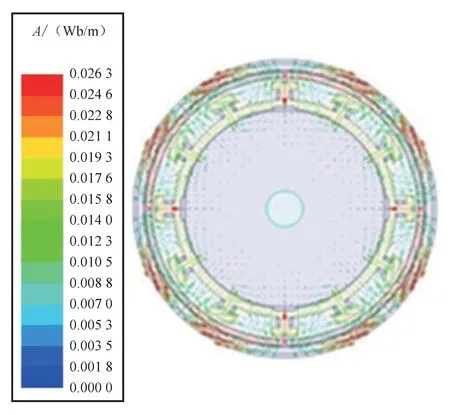
图16 自转模块的瞬态磁密矢量图
Fig.16 Transient magnetic density vector of the rotation module
图17为自转转矩随时间变化曲线,从图中可以看出,自转转矩在电机启动过程中存在一定的转矩脉动,峰值为80 N·m,时间大致出现在8 ms附近,随着电机运行逐渐趋于平稳,从50 ms附近开始,电机输出自转转矩趋于稳定,转矩值稳定在50 N·m附近,波动程度所占比例较小。自转转矩特性曲线较为理想,启动脉动时间短暂,且与稳定运行时的输出转矩相比,其突变程度不大,符合预期的要求。
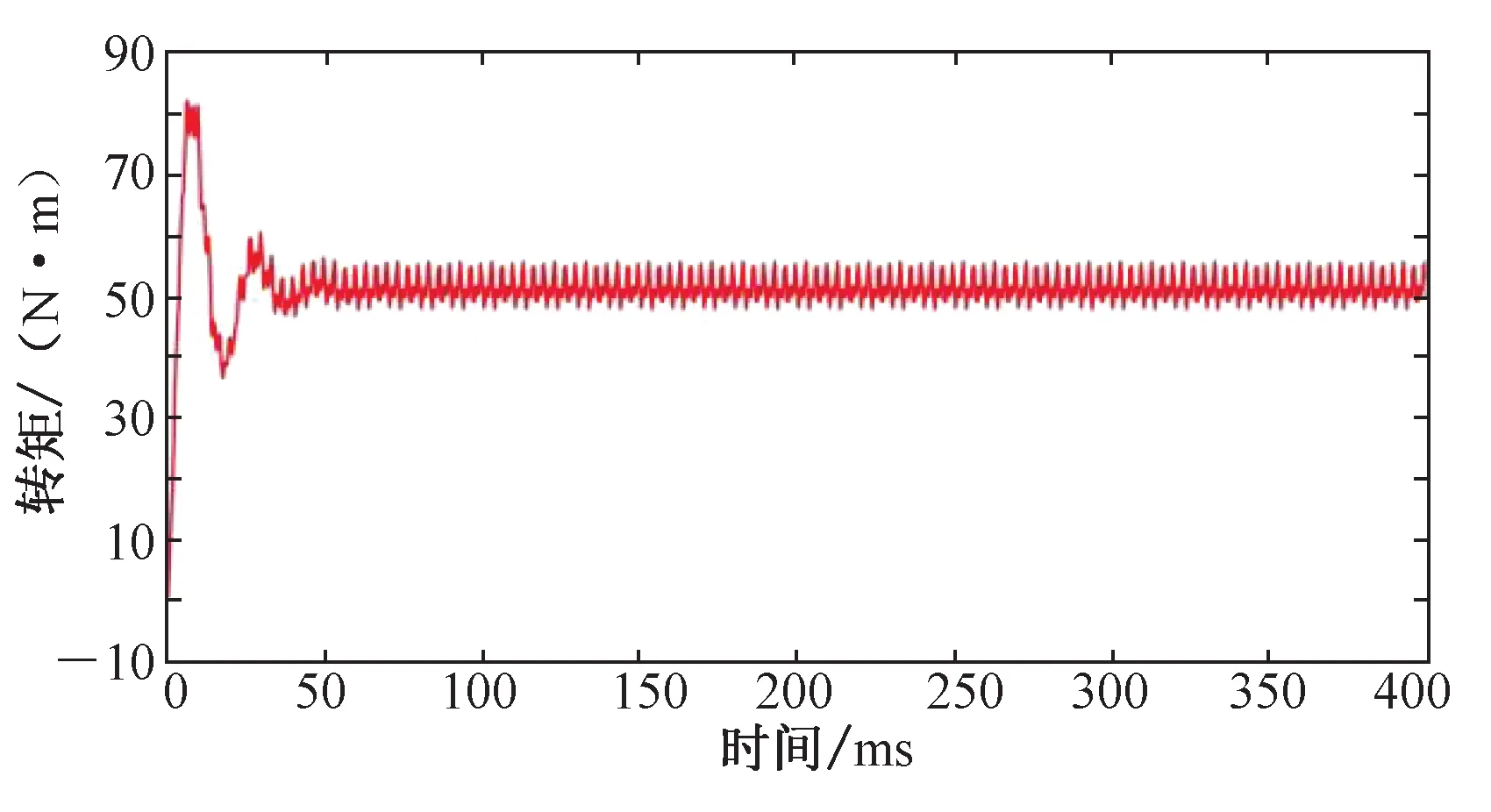
图17 电机自转的瞬态转矩
Fig.17 Transient torque of motor rotation
图18中红色点线为偏转转矩随时间变化曲线,以电机由静平衡位置沿X轴线倾斜为例,依靠集中式绕组的通电后产生的感应电动势与偏转永磁体相互作用,可逐次求解计算,即电机的偏转转子每绕X轴倾斜1°时,进行一次有限元计算,得到偏转模块于不同位置处的电磁转矩。电机偏转模块的倾斜范围为±15°。图18中的蓝色虚线为偏转转矩的期望值,应不低于1.6 N·m,红色曲线为偏转转矩随时间分布曲线,从图中可以看出,为了使偏转转矩输出值保持在1.6 N·m以上,偏转转矩一个通电策略的延续偏转角度应不大于-5°~5°,即为偏转运动通电策略应设为每倾斜10°改变一次。

图18 电机偏转的瞬态转矩
Fig.18 Transient torque of motor deflection
图19为自转绕组反电动势波形图,从图中可以看出,反电动势呈正弦趋势分布,峰值为450 V,一个正弦变化周期为20°,ABC三相反电动势变化规律相同,相间相位夹角为10°。除在电机启动时刻有稍许的波动外,电机平稳运行时波形较为理想。从图中还可以看出,反电动势波形受到一定的谐波影响,电机的后续优化可以从抑制反电动势谐波入手,从而达到优化电机磁路的效果。

图19 电机自转绕组的瞬态反电动势
Fig.19 Transient back electromotive force of motor self-rotating winding
图20为绕组磁链示意图,由于该电机绕组反电势为绕组磁链对时间求导而得,因此反电动势波形应与磁链分布波形近似,较好地验证了这一观点,印证了该电机有限元结构模型的准确性。

图20 电机自转绕组的瞬态磁链
Fig.20 Transient flux linkage of motor self-rotating winding
4 结论
本文提出了一种新式混合驱动型的三自由度电动机。分别分析了偏转型电动模块与自转型电动模块。基于分析不同充磁方式下的电磁损耗后,采用Halbach阵列的充磁方式对自转永磁体进行了优化,得到了正弦性更高的气隙磁密,并实现了对磁环外侧自我屏蔽与零磁干扰。基于电机单独自转与偏转的工作机理,分别分析了静磁场下对应的磁场分量,使用有限元法计算了电机自转运行时的磁链与反电动势,并于瞬态磁场下分析了电机自转与偏转空载运行的转矩,印证了建立该电机有限元结构模型的准确性。
