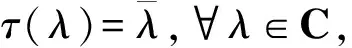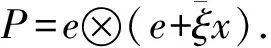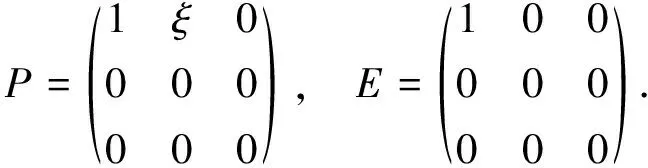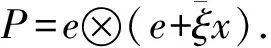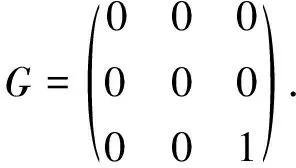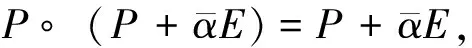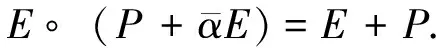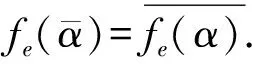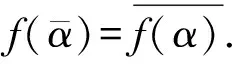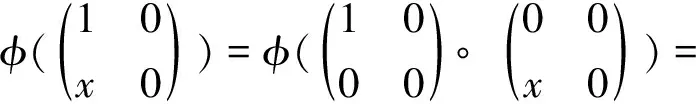B(H)上保持*-拟积的双射
2019-11-09宋显花
宋显花
(青海师范大学 数学与统计学院, 青海 西宁 810008)
近年来,算子代数中保持某种特征不变的映射的刻画问题一直备受关注,即寻找一些特征作为算子代数的同构不变量.特别地,众多学者研究了算子代数上关于Lie积和Jordan积等与非结合代数运算相关的保持问题,而且将这些运算和*-运算结合起来构造了一些同构不变量[1-3].另一方面,设R是环,∀a,b∈R,定义a∘b=a+b-ab,称∘为环R上的拟积.易知(R,∘)是半群,其单位元是零元0.设[a,b]=ab-ba是a、b的Lie积,则有[a,b]=b∘a-a∘b,即a、b的Lie积[a,b]是拟积意义下b、a的Lie积,因此,拟积与Lie积有密切的联系.同时,拟积在环或代数的结构研究中有非常重要的作用,如研究环的Jacobson根以及代数Lie拟幂零性等[4-6].文献[7-8]讨论了与拟积有关的保持问题.设X是复Banach空间,B(X)是X上有界线性算子全体得到的Banach代数,王宇平等[8]证明了当dimX≥2时B(X)上满足φ(A∘B)=φ(A)∘φ(B),∀A,B∈B(X)的双射φ是环同构.本文将拟积与*-运算相结合,刻画了B(H)上满足φ(A*∘B)=φ(A)*∘φ(B),∀A,B∈B(H)的双射.
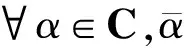
1 主要定理及证明
设H是维数大于1的复Hilbert空间,B(H)是H上有界线性算子全体组成的代数.∀A,B∈B(H),定义B(H)上的拟积为A∘B=A+B-AB.设φ是B(H)上的双射且满足
φ(A*∘B)=φ(A)*∘φ(B),
∀A,B∈B(H),
(1)
则称φ保持*-拟积.下面讨论这类双射的特征,为此先给出以下命题.
命题 1.1设φ是B(H)上保持*-拟积的双射,则以下结论成立:
1)φ(I)=I,φ(0)=0;
2)φ双边保持投影;
3)φ双边保持投影的序和正交性;
4)φ双边保持一秩投影和一秩算子.
证明1) 首先,由I∘I=I知
φ(I)=φ(I*∘I)=φ(I)*∘φ(I)=
φ(I)*+φ(I)-φ(I)*φ(I),
从而
φ(I)*=φ(I)*φ(I)=φ(I),
φ(I)2=φ(I),
即φ(I)是投影.又因为∀A∈B(H),有
φ(I)=φ(A*∘I)=φ(A)*∘φ(I)=
φ(A)*+φ(I)-φ(A)*φ(I),
所以φ(A)=φ(I)φ(A),∀A∈B(H).又由φ是满射知B=φ(I)B,∀B∈B(H).于是由Dauglas值域包含定理知R(B)⊆R(φ(I)),∀B∈B(H),取B=I可得R(φ(I))=H,故φ(I)=I.其次,由φ是满射知存在A∈B(H)使得φ(A)=0,从而由0∘A=A和(1)式知φ(0)=0.
2) 首先,设A=A*∈B(H),则
φ(A)=φ(A∘0)=φ(A*∘0)=φ(A)*,
即φ保持自伴算子.反之,∀B∈B(H),若φ(B)是自伴算子,则
φ(B*)=φ(B*∘0)=
φ(B)*∘φ(0)=φ(B)*=φ(B),
从而由φ的单射性知B=B*.于是φ双边保持自伴算子.其次,设P∈P(H),则φ(P)=φ(P)*.又因为
φ(P)=φ(P∘P)=
φ(P)∘φ(P)=2φ(P)-φ(P)2,
所以φ(P)2=φ(P),即φ(P)∈P(H).同理可证φ-1保持投影.
3) 首先,设P,Q∈P(H)且P≤Q,则φ(P),φ(Q)∈P(H).由Q∘P=P∘Q=Q知
φ(Q)=φ(Q)∘φ(P)=
φ(Q)+φ(P)-φ(Q)φ(P),
从而φ(P)=φ(Q)φ(P).同理可得φ(P)=φ(P)φ(Q).故φ(P)≤φ(Q).于是φ保持投影的序,同理可证φ-1保持投影的序.其次,设P,Q∈P(H)且P⊥Q,则P∘Q=Q∘P,从而
φ(P)φ(Q)=φ(Q)φ(P)∈P(H).
令E=φ(P)φ(Q).若E≠0,则令F=φ-1(E),从而E≤φ(P),E≤φ(Q)且F≤P,F≤Q,故由P⊥Q知F=0,矛盾.因此E=0,从而φ保持投影的正交性.同理可证φ-1也保持投影的正交性.
4) 首先,设P∈P1(H),则φ(P)∈P(H).若rankφ(P)>1,则存在非0的Q∈P(H)使得φ(Q)∈P1(H)且φ(Q)<φ(P),从而Q φ(B)=φ(A)*∘φ(B)= φ(A)*+φ(B)-φ(A)*φ(B). 于是φ(A)*=φ(A)*φ(B)是一秩算子,从而φ(A)是一秩算子.同理可证φ-1保持一秩算子. 定理 1.2若H是复Hilbert空间且dimH≥2,则φ是B(H)上保持*-拟积的双射的充要条件是当dimH≥3时,存在H上的酉算子或共轭酉算子U使得 φ(A)=UAU*,A∈B(H); 当dimH=2时,存在H上的酉算子U使得 φ(A)=UAτU*,A∈B(H). 证明充分性是显然的,故只需要证明必要性.当dimH≥3时,由命题1.1知φ是P(H)上的双射且双向保持投影的正交性,从而由文献[2]中的引理2.3知存在H上的酉算子或共轭酉算子U使得 φ(P)=UPU*,P∈P(H). 令 ψ(A)=U*φ(A)U,A∈B(H), 则ψ和φ有相同的性质,且ψ(P)=P,∀P∈P(H).以下证明ψ(A)=A,A∈B(H). 首先,分几个断言证明ψ(A)=A,A∈F1(H). 断言 1对于任意一秩幂等算子P有ψ(P)=P. H=[e]⊕[x]⊕[e,x]⊥ 下有 令 由E∘P=E知E∘ψ(P)=E,从而ψ(P)=Eψ(P),于是 a21=a22=0,A23=A31=A32=A33=0. 令 则由F∘P=P知Fψ(P)=F,从而 A13=0,a12=ξ,a11=1. 因此ψ(P)=P. 断言 2对于任意一秩幂零算子A,有ψ(A)=A. 设A=x⊗y是一秩幂零算子且不妨设‖x‖=1.令P=x⊗x,由P∘A=P知ψ(A)=Pψ(A).又因为ψ保一秩算子,所以可令ψ(A)=u⊗v,从而 u⊗v=(x⊗x)(u⊗v)=〈u,x〉x⊗v, 故u与x线性相关,不妨设u=x,于是ψ(A)=x⊗v.令B=y⊗y/‖y‖2,则B和A+B都是一秩幂等算子且B∘A=B+A,从而由断言1知 ψ(A)-Bψ(A)=A, 因此v=y.于是ψ(A)=A. 断言 3∀α∈C,P是非自伴的一秩幂等算子,有ψ(αP)=αP. H=[e]⊕[x]⊕[e,x]⊥, 在此分解下令 由E∘αP=E知 ψ(αP)=Eψ(αP), 从而 x21=x22=0,X23=X31=X32=X33=0. 由αP∘G=G∘αP知 即 从而 X13=Y13=Y23=0. 注意到αP∘P=P∘αP,从而 故 x12=x11ξ,Y31=Y32=Y33=0. 因此 于是存在C上的双射gP使得ψ(αP)=gP(α)P.设P=x⊗y是非自伴的一秩幂等算子,则由dimH≥2知存在非0向量z∈H使得〈x,z〉=0.令N=x⊗z,则αP∘N=αQ,其中 是非自伴的一秩幂等算子,因此 于是 ψ(αP)+N-ψ(αP)N=ψ(αQ), 即 gP(α)P+N-gP(α)N=gQ(α)Q, 易得 gP(α)=gQ(α)=α, ∀α∈C. 因此ψ(αP)=αP. 断言4∀α∈C,E∈P1(H),有ψ(αE)=αE.由前面的讨论可知α=0,1时结论成立,于是设α∈C{0,1}.设 E=e⊗e∈P1(H), 则存在P,Q∈P(H)使得I=P⊕E⊕Q,于是有空间分解 H=PH⊕EH⊕QH. 在此空间分解下令 注意到 P∘(P+αE)=P+αE, E∘(P+αE)=E+P, (P+αE)∘P=P+αE, ψ(P+αE)=P+a22E, 从而存在C上的双射fe使得 ψ(P+αE)=P+fe(α)E, 另外,由 ψ(Q+αE)=Q+ge(α)E. 由 P∘(Q+αE)=Q∘(P+αE) 易得ge=fe.于是 ψ(Q+αE)=Q+fe(α)E. 应用类似的方法得到 ψ(P+Q+αE)=P+Q+fe(α)E. 令 由 知 从而 C31=C32=C33=0, 由α的任意性知fe(α)≠1,从而C21=C23=0.由 易得C11=C12=C13=0.于是存在C上的双射he使得 ψ(αE)=he(α)E. 由 P∘αE=P+αE 易知 he(α)=fe(α). 另外,注意到 (P+Q)∘(αI)=P+Q+αE, 从而Eψ(αI)=fe(α)E,即 e⊗eψ(αI)=fe(α)e⊗e, 是单位向量,于是有 ψ(αI)=fe(α)I, ∀e∈H 是单位向量,即fe(α)与e的选取无关.令fe=f,则 ψ(αI)=f(α)I,ψ(αE)=f(α)E, ∀α∈C, ∀E∈P1(H), 是非自伴的一秩幂等算子,从而f(α)E∘N=αQ,即 f(α)=α. 其次,用文献[8]的方法类似可证 ψ(A)=A,A∈F(H). 最后,若dimH=∞,则证明 ψ(A)=A,A∈B(H). 设A∈B(H),则 (I-E)∘A=(I-E)∘EA, ∀E∈P1(H), 从而 Eψ(A)=EA, ∀E∈P1(H). 于是ψ(A)=A.因此当dimH≥3时,有φ(A)=UAU*,A∈B(H). 以下假设dimH=2,则φ是M2上的双射且保持*-拟积.设Eij(i,j=1,2)是M2的标准基,即 Eij=(ekl),eij=1, ekl=0, ∀(k,l)≠(i,j). 由命题1.1知φ(E11)和φ(E22)是2个相互正交的一秩投影,则存在酉算子U1∈B(H)使得 令 则ψ1与φ有相同的性质且 ψ1(Eii)=Eii,i=1,2. 因此不妨设 φ(Eii)=Eii,i=1,2. ∀α∈C,令 则由E11∘αE11=E11知 E11φ(αE11)=φ(αE11), 从而a21=a22=0.令 由 E22∘αE11=αE11∘E22 知 于是 从而 因此 从而存在C上的双射τ11使得 易证 应用类似的方法可知存在C上的双射τ22使得 φ(αE22)=τ22(α)E22, 令 由E11∘αE12=E11容易计算c21=c22=0.又因为 E22∘αE12=E22+αE12∈F1(H), 所以 从而c11=0.因此φ(αE12)=c12E12,从而存在C上的双射τ12使得 φ(αE12)=τ12(α)E12. 同理可证存在C上的双射τ21使得 φ(αE21)=τ21(α)E21. ∀x,y∈C,有 xE12∘yE12=(x+y)E12, 从而 于是 (2) 同理由xE21∘yE21=(x+y)E21得 (3) 由 xE21∘yE11=yE11∘(x-xy)E21, xE12∘yE22=yE22∘(x-xy)E12 容易计算 (4) (5) 以上2式中分别取y=0得到 (6) 于是由(2)、(3)和(6)式知τ12、τ21可加.由(4)~(6)式易得 τ21(x-xy)=τ21(x)-τ21(x)τ11(y), (7) τ12(x-xy)=τ12(x)-τ12(x)τ22(y), (8) 由(7)、(8)式及τ12、τ21的可加性得 τ12(-xy)=-τ12(x)τ22(y), τ21(-xy)=-τ21(x)τ11(y). 因此以上2式中取y=1可得 τ12(-x)=-τ12(x),τ21(-x)=-τ21(x). 于是 τ12(xy)=τ12(x)τ22(y), τ21(xy)=τ21(x)τ11(y), (9) 从而 因此有 τ21(x)τ22(y)=τ21(x)τ11(y), ∀x,y∈C, 故τ11=τ22.记τ22=τ11=τ.(9)式中取x=1,得到 τ12(y)=τ12(1)τ22(y), τ21(y)=τ21(1)τ11(y). (10) 下面证明τ12(1)τ21(1)=1.取 令 由 知 (11) (12) 又因为 (13) (14) 所以由(11)和(13)式知a12=τ21(x),a22=0.由(12)和(14)式知 a11=τ(x2),a12=-τ12(x), 于是 又因为 φ(A)=φ(-xE12∘xE21)= 所以 τ(x2)=τ12(x)τ21(x), 取x=1可得τ12(1)τ21(1)=1. 下面证明τ是环同构.由(10)式及τ12可加知 (τ(x)+τ(y))τ12(1)=τ12(1)τ(x+y), 从而由τ12(1)≠0知τ可加.又由(9)和(10)式知 τ(xy)τ12(1)=τ12(1)τ(x)τ(y), 从而τ可乘.因此τ是环同构.令 则U2是酉算子,且 令 则ψ2与φ有相同的性质且 ψ2(αEij)=τ(α)Eij,i,j=1,2. 设 由 知 (15) 又因为 (16) (17) 所以由(15)~(17)式知bij=τ(aij),i,j=1,2.因此ψ2(A)=Aτ.令U=U1U2,则U是酉算子且 φ(A)=UAτU*, ∀A∈M2. 致谢青海师范大学校级项目(2018ZR004)对本文给予了资助,谨致谢意.