基于混合拉普拉斯模型和EM算法的图像降噪方法

张正杰

（苏州市轨道交通集团有限公司，苏州 215004）

一般来说，图像在生成和传输过程中常常因受到各种噪声的干扰和影响而使图像降质，这对后续图像的处理将产生不利影响。噪声可以理解为“妨碍人们的感觉器官对所接受的信源信息理解的因素”。目前，图像去噪在数字图像处理技术中的重要性越加明显。

近年来，小波理论得到了非常迅速的发展，而且由于其具备良好的时频特性，因而实际应用也非常广泛。在去噪领域中，小波理论也同样受到了许多学者的重视，他们应用小波进行去噪，并获得了非常好的效果[1、2]，具体来说，小波去噪方法的成功主要得益于小波变换具有如下特点[3]：（1）低熵性（2）多分辨率 （3）去相关性（4）选基灵活性。基于这些特点，提出一种基于混合拉普拉斯模型和EM算法的图像降噪方法。

1 小波去噪问题的描述

设噪声图像 G（i，j）=X（i，j）+n（i，j），降除噪声的问题可以认为是如何将X（i，j）从G（i，j）中恢复出来。对噪声图像进行小波变换后得到WG（i，j）=WX（i，j）+n（i，j）。

常用的传统的低通去噪滤波方法有滑动平均窗（均值滤波方法）、线性滤噪、中值滤波、基于秩-阶滤波（排序量）的方法、基于马尔可夫场模型[4]和基于偏微分方程（PDE）的方法[5]等。用这些方法可以去除大部分的噪声小波系数，同时较好地保留图像的高频细节信号。但仔细分析，不难发现，用这种方法去噪，并没有考虑图像本身的能量分布特点，不可避免地会造成各个子带去噪的不平衡，不利于图像的恢复。

2 最大后验估计与混合拉普拉斯模型

2.1 最大后验估计

设噪声图像g=x+n，其中，n是独立的均值为0的高斯白噪声，g是观测到的含有噪声的信号，x是不含噪声的原始信号，而在小波域问题就可以被描述成：y=w+n，其中，y是观测到的含噪信号的小波系数，w是无噪原始信号的小波系数，n为独立的均值为0的高斯白噪声。

w的最大后验估计定义为

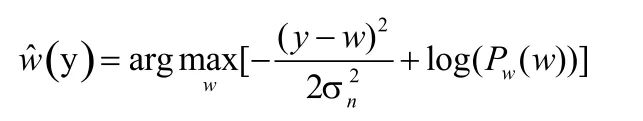
定义f（w）=log（Pw（w），这样通过对对上式求导，并令其为0，即：

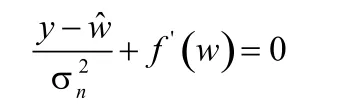
便能够得到w的最大后验估计。

2.2 单一拉普拉斯模型

有了w的最大后验估计，接下来便要估计观测信号小波系数的分布模型，若假设无噪信号的小波系数服从单一的拉普拉斯概率密度函数，则：

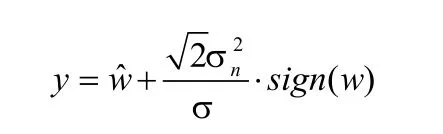
2.3 混合拉普拉斯模型

若假设无噪信号的小波系数服从混合拉普拉斯概率密度函数，可得

与y的关系可以表示为：

2.4 混合概率密度函数

本小节将一个拉普拉斯概率密度函数与一个高斯概率密度函数的卷积表示成一个概率密度函数，以方便下节用EM算法进行参数计算。将y=x*n（“*”代表卷积）的概率密度函数简记为，可得：

3 EM算法

混合模型会有比单独的概率密度函数更多的参数，而随着参数数量的增加，通过观测信号对参数的估计的准确度就会降低，所以选择适量的参数并对其进行准确的估计很重要，现引入EM算法来解决参数估计的问题。

3.1 EM Algorithm

设给定的训练样本是x={x1，x2，…，xm}，样本间相互独立，我们想找到每个样本隐含的类别z，能使得p（x，z）最大。EM是一种解决存在隐含变量优化问题的有效方法。对于每一个样本i，让Qi表示该样本隐含变量z的某种分布，Qi满足的条件是根据Jensen不等式，要想让等式成立，需要让随机变量变成常数值。对式子做进一步推导可以得到一般的EM算法的步骤如下：

循环重复直到收敛

{

（E步）对于每一个i，计算：

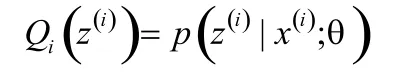
（M步）计算：

}

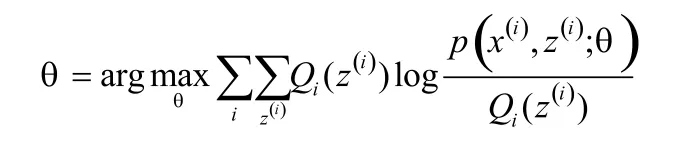
即E步固定θ，优化Q，M步固定Q，优化θ，循环直至收敛。

3.2 EM算法求解混合拉普拉斯模型参数

E-step：

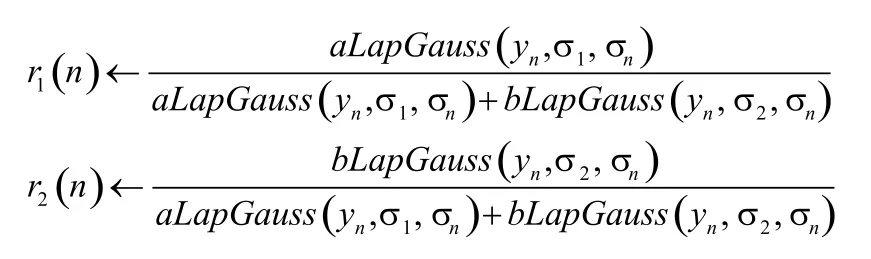
M-step：

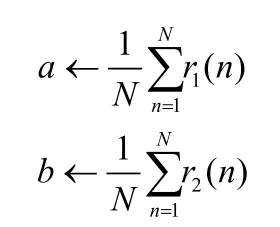
估计混合模型的方差：

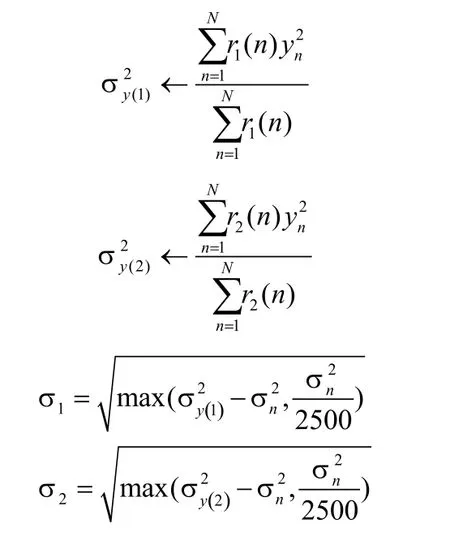
4 实验结果

本论文采用的无噪图像是一张大小为512×512像素的灰色标准测试图，只经过灰度化将图像的三维矩阵转换成一维矩阵。

4.1 无噪图像小波系数模型验证

本节验证无噪图像的小波系数是否符合提出的混合拉普拉斯模型，对于混合模型参数的估计也采用EM算法。其结果如图1-3所示，其中图1代表无噪图像第一层小波系数的分布直方图，图2代表无噪图像第二层小波系数的分布直方图。

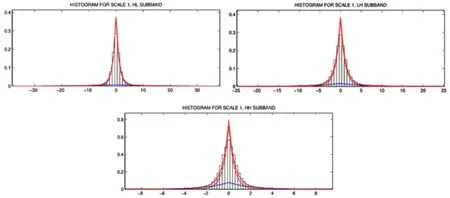
图1 无噪图像第1层小波系数的分布直方图

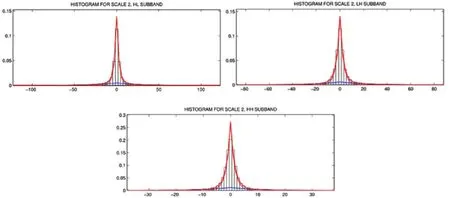
图2 无噪图像第2层小波系数的分布直方图

从结果来看，无噪图像的小波系数近似符合混合拉普拉斯模型，由EM算法迭代出的参数也符合图像小波系数的分布。

4.2 噪声图像小波系数验证

本节验证叠加了噪声的图像经小波变换后的小波系数的分布，是否符合混合Lapgauss概率密度函数，叠加的噪声标准差为10。结果分别如图3-6所示。其中图3代表含噪图像第一层小波系数的分布直方图，图4代表含噪图像第二层小波系数的分布直方图。

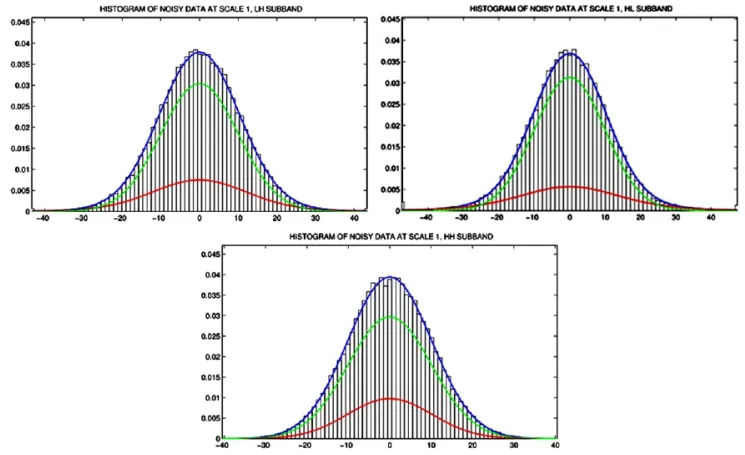
图3 含噪图像第1层小波系数的分布直方图

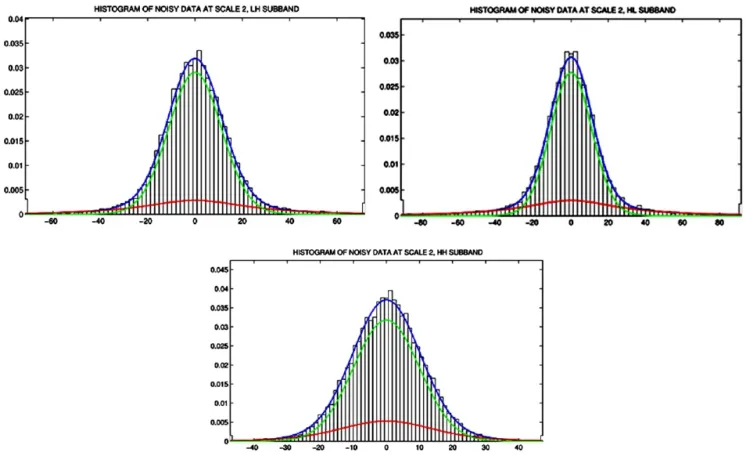
图4 含噪图像第2层小波系数的分布直方图

从结果来看，噪声图像的小波系数分布也符合混合Lapgauss概率密度函数。

4.3 图像降噪结果

降噪效果分析

经过降噪处理后的图像其均方根误差为3.7，相较于叠加的高斯白噪声标准差为10，经过处理后，图像的噪声大小下降了近66.67%，取得了较为不错的效果。

5 结束语

本文给出了一种基于图像小波系数分布方法的图像降噪方法。对实际的标准测试图像的降噪过程中，验证其近似符合混合拉普拉斯模型，并利用EM算法计算混合模型的参数，原理简单、算法清晰、流程明确，在对图标准图像的测试中也取得了较为理想的效果，能够有效并且快速地对图像进行降噪处理。

但是在本文提出的方法中，主要考虑了当图像较为符合混合拉普拉斯模型的情况。若图像的小波系数为其他的分布，或者噪声为其他分布时，相应的结果便不会很理想，所以对模型以及相应的公式推导还有很大的提升空间。