指廊式航站楼风荷载特性的CFD数值计算方法定量研究

黄政 颜卫亨

(1.中国市政工程华北设计研究总院有限公司 天津300074； 2.长安大学建筑工程学院 西安710061)

引言

指廊式航站楼在风荷载作用下表面气动特性十分复杂[1-3]，虽然组成航站楼的各单体外形较为规则，但由于其组合体形状不规则且体量大，周围风场绕流复杂，指廊所形成的U 形区域内涡流交织，故其表面风压分布特征和周围湍流流场呈现出较强的复杂性，同时航站楼屋盖具有质量轻、阻尼小等抗风不利因素，因此往往对风致响应十分敏感，属风敏感结构，风荷载成为结构设计和分析的主要荷载之一。 对于此类复杂体型建筑，除了常用风洞试验外，CFD (Computational Fluid Dynamics)数值风洞计算技术可以高效和方便地对建筑表面风压分布和周围湍流流场进行预测分析，由于其周期短、费用低而被广泛应用[4-9]。 目前CFD 的技术水平，可实现对简单形体表面风荷载预测的实用化； 对于复杂形体还未达到像风洞试验那样的可信度。 新的CFD 计算方向，是将其用于复杂形体并展开相应的技术研究[10]。 文献[5]研究了大跨度张弦梁屋盖结构的风致响应，相关成果可为具有类似形体结构的抗风设计和研究提供理论基础。 文献[7]采用LES方法对复杂大跨屋盖结构的风荷载进行了CFD数值计算分析，建立了基于 CFD 数值计算的复杂体型大跨屋盖结构风荷载的预测方法。 文献[9]以昆明新机场的指廊式航站楼为背景，采用CFD 计算技术获取结构风载体型系数，可应用于工程结构抗风的初步设计。 尽管国内外关于多种体型建筑表面风压分布特性已经有了分析和研究，但针对指廊式航站楼建筑的CFD 数值风洞的基础性研究相对薄弱，关键技术及参数的选取缺少全面而系统的分析与探讨，故亟需对复杂体型的指廊式航站楼建立基于CFD 的抗风设计计算方法。

本文采用CFD 数值风洞计算技术，以指廊式航站楼为研究对象，确定CFD 数值计算的网格划分技术、湍流模型选取、离散格式和求解算法等关键技术及参数的选取。 从而可采用CFD数值风洞计算技术改善复杂体型结构的抗风特性，探究指廊式航站楼在风力作用下合理的建筑气动外形。 通过建筑形体的自适应来降低结构的风致响应，使结构具有良好的抗风性能和合理的气动外形。 在建筑设计时做到美学和空气动力学的完美结合，为风荷载作用下建筑设计方案和结构体型优化提供设计方法和理论依据。 此外，根据CFD 数值计算结果可以指导风洞试验模型测点的布置，进而进行结构的风荷载计算和分析。

1 CFD数值风洞计算方法定量研究

指廊式航站楼建筑(图1)主要包括以下几部分：航站楼、南一指廊、南二指廊、南连接楼、北连接楼及南过街楼和北过街楼。 航站楼长为345m，宽为 115m，屋面最高处为 36.5m，长高比约为10∶1。 南一指廊和南二指廊长约180m，宽约 40m，屋面最高处为 16m，长高比约为11∶1。 南连接楼长为 362m，最宽处约 85m，中部宽约为40m，屋面最高处为16m，长高比约为22∶1，总建筑面积为265817m2。

图1 航站楼建筑三维立体效果图Fig.1 Terminal three-dimensional renderings

文献[11]完成了航站楼屋盖表面压力测量风洞试验。 测压试验模型为刚体模型，风洞试验模型缩尺比为1∶220。 测压试验风向角转动方向和屋面几何分区如图2 所示。 试验共完成B 类地面粗糙度类别下风速为 13m/s、从 0° ～ 360°每隔15°共24 个风向角下的测压试验。

图2 航站楼几何分区及风向角Fig.2 Partition and wind direction of terminal

此类航站楼建筑具有体量大、长高比大(最小值为10∶1，最大值为22∶1)和形体复杂等特征。 为此，采用AutoCAD 软件建立航站楼建筑模型，再将其导入 Gambit 能识别的sat 文件格式。由于AutoCAD 软件与Gambit 软件在识别精度上有差别，因此，还需对几何模型运用 Gambit 中的虚几何技术和修剪技术来对模型进行进一步的修正和完善，消除模型中存在的尖角、短边、缝隙等，精细而高效地实现模型的网格划分。

目前理论流体力学和数值计算技术在模拟复杂钝体分离流动方面还不够完善，CFD 计算结果精度受到数值模型自身以及数值迭代算法等诸多因素的影响[12，13]。 因此，为确保解具有足够的稳定性，需深入探讨CFD 计算技术的关键基础性理论。 以风洞试验的B 类地面粗糙度类别下风速为 13m/s、90°风向角时工况为例[11]，进行 CFD数值风洞计算方法定量研究，建立指廊式航站楼CFD 的抗风设计方法。

1.1 计算域的确定

计算域的选定应在满足湍流充分发展的前提下，尽量减少边界对计算结果的影响。 指廊式航站楼建筑在风力作用下主要以顶面绕流为主，在参考文献[12]的基础上建议入口距建筑物迎风面宜大于5h(h=36.5m，即建筑物的最大高度)的距离，建筑物的顶面和侧面距离计算域边界宜大于4h，并且保证其最大阻塞率不大于3%。 背风面距离出口应使湍流达到完全发展的状态，一般要求大于9h。

1.2 网格划分技术

网格划分应精细到足够捕捉涡、剪切层等物理现象特征的变化，网格质量也需足够高以期能够获得较好的计算精度。 针对指廊式航站楼建筑的形体特征，网格划分方案采用分区划分网格技术与尺寸函数(size function)网格技术相联合的方法。 网格类型采用适合于复杂边界形状的流场分析的非结构化网格。 网格单元采用主要由四面体网格构成，但在局部凹凸及转角区域为六面体、锥形和楔形网格的网格单元Tet/Hybrid，进一步采用网格光顺技术提高网格质量，可以使网格更加均匀，提高了计算结果的收敛性和稳定性。 为探讨适合指廊式航站楼建筑的最优size function和网格数量，实现网格离散由密到疏的过渡，对航站楼在24 个不同风向角下采用size function 进行网格划分，并对航站楼进行数值计算分析。 主要探讨航站楼屋盖的1 区～9 区和指廊区11 区～13 区，研究网格单元数量对计算结果的影响，其计算结果如图3 所示。

图3 网格单元数量对平均风压系数的影响Fig.3 Influence of grid numbers on the average wind pressure coefficient

由图3 分析可知，网格单元的数量并不影响结构表面分区平均风压系数的变化趋势，但在数值计算精度上具有较大的差距。 核心区网格单元数量为60 万时误差最大。 当网格单元数量达到120 万左右时，计算结果与风洞试验结果基本吻合。 当网格单元数量达到150 万时，计算结果与风洞试验更加吻合，但是计算精度提高有限，并且随着网格单元数量的增加，计算时间将明显增加，计算效率降低。 因此，为节约计算耗时且同时满足计算精度要求，最终确定航站楼建筑在24个不同风攻角下最小网格单元尺寸为0.01m，size function 的增长比控制为 1.2 ～ 1.3，最大网格单元尺寸控制为0.5m ～0.8m，计算域核心区的网格单元数量控制为120 万～150 万。 计算域核心区以外的影响区网格单元最大尺寸取为3m，整个计算域的网格单元数量控制为180 万 ～200 万。

1.3 湍流模型的选取

工程上常采用平均Navier-Stokes 方程[10]来计算流体的湍流流动：

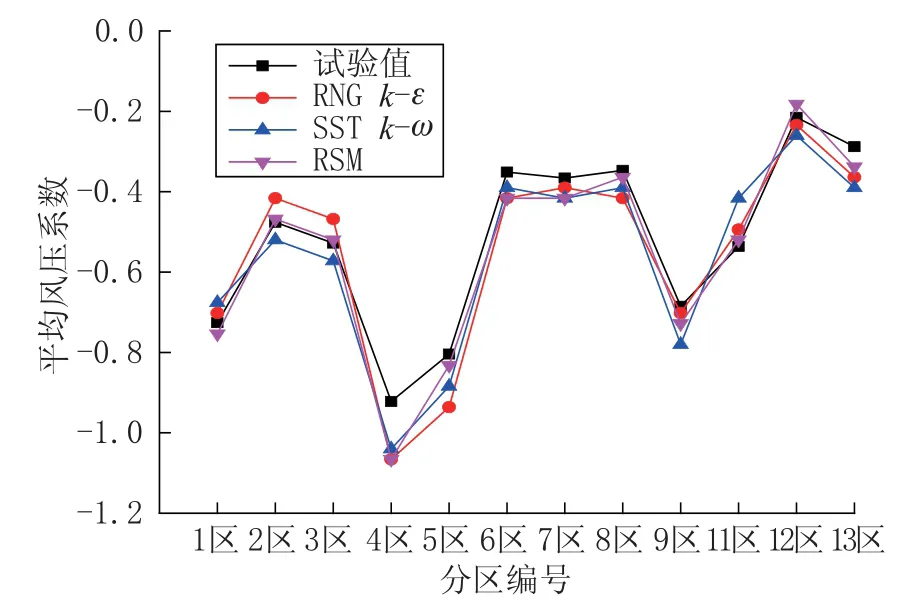
图4 湍流模型对平均风压系数的影响Fig.4 Influence of turbulence models on the average wind pressure coefficient

由图4 分析可知，3 种湍流模型在预测指廊式航站楼流场流动的大致趋势是一致的，在计算精度上相比于RNGk-ε模型和SSTk-ω模型，RSM 模型计算结果较为精确，这是因为RSM 模型比双方程k-ε系列模型更严格考虑了漩涡、流线型弯曲等特征，对于复杂流场分析预测精度更高，但RSM 模型要联合雷诺压力和层流，故计算效率相对较低。 在PC 计算机进行流体计算分析时，常采用 RNGk-ε模型和 SSTk-ω模型，RNGk-ε湍流模型是为高张力引起的湍流粘度降低而设计的，这是RNGk-ε湍流模型的缺点。 由于SSTk-ω湍流模型考虑了湍流剪切应力在逆压梯度边界层的输运，更适合模拟钝体结构的分离流动，综合文献[14 -16]分析，建议在计算指廊式航站楼建筑物平均风力作用时，采用能满足精度且计算方便的SSTk-ω湍流模型。

1.4 离散格式和求解算法的影响

在离散方程中对流项的离散格式常用的有二阶迎风格式和QUICK 格式，二阶迎风格式可以有效减小数值扩散误差，QUICK 格式具有三阶精度的截差。 为了探究两种对流项的离散格式对指廊式航站楼流场计算分析的影响，其CFD 数值计算结果如图5 所示。

图5 离散格式对平均风压系数的影响Fig.5 Influence of discrete format on the average wind pressure coefficient

由图5 分析可知，QUICK 格式和二阶迎风格式对航站楼建筑表面平均风压计算结果总体上影响较小，QUICK 格式比二阶迎风格式可以获得更好的计算精度，减少假扩散误差，各分区平均风压系数与风洞试验数据基本一致，可有效地改善航站楼建筑绕流的压力场计算结果。

工程上应用最为广泛的流场计算求解方法有SIMPLEC 算法和 PISO 算法，SIMPLEC 算法通过改进通量修正方法，有效地提高了计算收敛速度。 而PISO 算法增加了一个修正步，更好地同时满足动量方程和连续方程。 求解算法对航站楼建筑计算结果的影响如图6 所示。

图6 求解算法对平均风压系数的影响Fig.6 Influence of solution algorithm on the average wind pressure coefficient

由图6 分析可知，SIMPLEC 算法和 PISO 算法对航站楼建筑表面平均风压的计算结果总体上影响较大，SIMPLEC 算法与风洞试验结果更吻合，PISO 算法与风洞试验结果误差较大，可见PISO 算法是针对非稳态可压流动的无迭代计算所建立的压力速度计算程序，但对于指廊式航站楼所形成的网格歪斜度较大时，计算精度并不高，而对于指廊式航站楼的稳态问题，SIMPLEC算法更适合。

1.5 不同缩尺比模型的影响

由于指廊式航站楼建筑体量大，需要选取合适的缩尺模型，因为适宜的缩尺模型影响着计算域的确定和网格的划分。 为分析与探讨指廊式航站楼建筑模型在CFD 数值计算时缩尺比的合理选取，其计算结果如图7 所示。

图7 模型缩尺比对平均风压系数的影响Fig.7 Influence of model scale on the average wind pressure coefficient

由图7 分析可知，在指廊式航站楼建筑定常绕流流动计算中，模型几何缩尺比变化对平均压力分布特性的影响可忽略不计。 而模型缩尺比的选择通常由风洞试验的试验段截面尺寸决定。 在CFD 数值风洞的分析中，模型缩尺比过小，由于钝体尖角、转角等的存在，在网格划分时需要用更小的网格尺寸去适应，且常存在网格歪斜度大、网格质量差等问题，常常引起网格不易划分成功。 模型缩尺比较大，计算域的增大会导致网格单元数量急剧增加，计算时间增加和计算效率降低。 在经过大量试算和分析的基础上，对于指廊式航站楼建筑CFD 数值分析的模型缩尺比取为1∶100。

1.6 CFD数值风洞计算参数选取

其他数值计算边界条件等参数的选取参考文献[13]。 综合 1.1 节 ～1.5 节 CFD 数值计算的基础性研究，确定指廊式航站楼CFD 数值风洞计算时参数的选取，如表1 所示。

表1 指廊式航站楼CFD 数值风洞计算参数的选取Tab.1 Calculation parameters selection for CFD numerical simulation of complex shape structure

续表

2 CFD数值计算方法精度评估

指廊式航站楼的大跨度曲面屋盖在体型上具有非对称性，且局部凹凸较大，因此建筑表面风压分布在不同风向角下表现出不同的规律性，而风向角是影响表面风压分布的主要因素。 因此，应分析风向角对建筑表面风压分布的影响。 图8给出了航站楼建筑在24 个全风向角下的平均风压系数的变化规律。

图8 风向角对平均风压系数的影响Fig.8 Influence of wind directions on the average wind pressure coefficient

由图8 分析可知，风向角是影响建筑表面平均风压分布的关键因素，在不同风向角下建筑表面分区平均风压系数具有较大的变化梯度，如航站楼的6 区～8 区在24 个不同风向角下表面风压具有相似变化趋势，其分区平均风压系数呈二次抛物线变化，在180°风向角时达到分区平均风压系数的极值。 因此，有必要对指廊式航站楼在全风向角下采用CFD 数值计算方法进行计算与分析，研究CFD 数值分析方法的可靠性和解的稳定性。 限于篇幅，现将每3 个风向角作为一组，其计算结果与风洞试验对比如图9 所示。

图9 两种方法计算平均风压系数对比Fig.9 Comparison of two methods average wind pressure coefficient

由图9 分析可知，在各风向角下CFD 抗风设计数值方法计算结果与风洞试验所得各分区的平均风压系数在分布规律总体上吻合较好，定性分析上符合结构表面风压分布规律，定量分析上整个航站楼建筑表面大部分区域的平均风压系数误差均小于20%，随着风向角的变化，误差呈现出一定的离散性，其中在指廊区域11 区、12 区、南连接楼13 区和航站楼6 区、7 区、8 区误差较大，约为30%。

由图9a、b、h 分析可知，在 0° ～60°和315°～345°风向角下表面平均风压系数与风洞试验结果相比，大部分区域的误差小于20%，在6 区、7 区、8 区，平均风压系数的数值计算结果均大于风洞试验结果，且误差约为 30%。 在 0° ～60°风向角下，表面风压变化规律具有一定的相似性，6 区、7 区、8 区的平均风压系数相对于其他区域较小，其值在 -0.2 ～ -0.4 范围变化，而在其他区域均具有较大的负风压。 但在0°和60°风向角下数值计算结果与风洞试验数据相比误差呈现一定的离散性，其中误差较大的区域共有5 个区域。 由图9b、c 分析可知，在 75°、90°、105°风向角下表面平均风压系数与风洞试验结果相比，绝大部分区域的误差小于20%，只在南连接楼13 区误差超过20%，且该区域平均风压系数的数值计算结果大于风洞试验结果。 由图9b ～g分析可知，在 120° ～285°风向角下表面平均风压系数与风洞试验结果相比，指廊区域11 区、12区和13 区误差约为30%，且这些区域平均风压系数的数值计算结果均大于风洞试验结果。 但在165°、240°和255°风向角下数值计算结果与风洞试验数据相比误差呈现一定的离散性，其中误差较大的区域共有6 个区域。

从误差较大的分区位置可以看出，对于指廊式航站楼建筑，CFD 数值模拟湍流物理模型在计算与分析分离较为严重、流场较为复杂时其计算结果并不是十分理想，存在一些计算误差较大的区域，计算时应引起足够的注意。 此外，网格的划分是影响CFD 数值风洞计算的重要因素。 网格尺寸常采用从内到外逐渐增大的方式，因此，不可能所有的网格尺寸和网格数量都能很好地模拟建筑周围风场的流动。 同时由于南一指廊、南二指廊和南连接楼形成半U 形区域，相互之间气动干扰作用强烈且风场分布复杂，进一步产生误差效应，且随着风向角的变化，误差呈现出强烈的不规律性。 故在CFD 数值风洞计算时，应建立与所分析建筑形体相适应的网格划分技术，选取合适的网格单元、网格大小和网格数量，尽可能减少由于网格因素所造成的计算误差，以提高数值计算的精度。

综上所述，尽管目前CFD 数值风洞还无法完全代替风洞试验技术，但将其作为建筑初步方案抗风设计和结构体型优化的辅助分析手段是可行的。 采用CFD 数值风洞技术对建筑表面风压进行初步研究，通过建筑形体的自适应来降低结构的风致响应，得到建筑在风荷载作用下较为合理的气动外形。

3 结论

1.指廊式航站楼CFD 数值计算时，网格划分宜采用分区划分网格技术与size function 网格技术相联合的方法，采用非结构化网格中Tet/Hybrid 网格类型，核心区最小网格单元尺寸宜为0.01m，size function 的增长比控制为 1.2 ～ 1.3，最大网格单元尺寸控制为0.5m ～0.8m，核心区的网格单元数量控制为120 万～150 万，核心区以外的影响区网格单元最大尺寸为3m，整个计算域的网格单元数量控制为180 万～200 万时CFD 计算结果较为理想。

2.指廊式航站楼CFD 数值计算时，湍流模型采用SSTk-ω模型，离散格式采用QUICK 格式，求解算法为SIMPLEC。 在定常流动计算中，模型缩尺比变化对平均压力分布特性的影响较小，对于大型指廊式航站楼宜取为1∶100。

3.在指廊式航站楼表面风荷载的抗风设计分析时，CFD 数值计算方法基本可以达到工程精度的要求，在建筑风场的定性分析上具有较好的吻合性，定量分析上也能达到一定的可靠度。 通过分析误差的原因，得出网格划分方式、湍流物理模型和航站楼各单体之间强烈的气动干扰作用是造成CFD 数值计算误差的主要原因，在计算和分析时应进行探讨与研究，确定合理的参数取值。

4.在建筑方案阶段，可以采用CFD 数值风洞计算方法对指廊式航站楼形体风压进行初步研究，获取表面平均风压系数和周围流场分布，作为结构选型和初步设计的依据，为建筑结构方案设计和结构体型优化提供一个设计方法。