危险品道路运输多目标路线优化研究

李树民 刘勇杰

摘要：根据危险品在道路运输过程中具有运输风险、运输成本、运输时间的多层属性，提出在运输网络规划中建立考虑三者因素的多目标优化模型。将运输风险划分为人员风险、财产损失、环境污染损失。从监管部门和危险品运输企业两者期望出发，建立运输企业运输费用最小、运输风险期望值最小和运输时间最短的多目标危险货物道路运输优化模型，用层次分析法确定三项指标的权重，结合MATLAB软件，用Dijkstra算法和集成目标函数最优折衷路径的扩展标号法对危险品运输多目标优化模型进行求解。最后通过实例分析验证模型有效性，为监管部门以及危险货物运输企业规划运输路线提供实际参考。

关键词：危险品道路运输;路径优4E;Dijkstra算法;扩展标号算法

中图分类号：U116.2 文献标识码：A

0引言

随着社会经济的快速发展，各类危险品的道路运输量也将逐年增加。危险物品道路运输路线的选择与路线周边的人口、环境、财产安全息息相关，因此受到政府监管部门的管制，在规划路网时，政府部门希望危险品运输在起讫点间总风险最小，而运输企业更多的会考虑降低运输成本与运输时间，所以，找到两者满意的均衡路径来保障运输安全与运输效益成为必要。

近年来，危险品道路运输安全问题受到各国政府及人民群众的高度关注，很多专家学者和科研机构对危险货物道路运输路网优化问题进行了广泛深入研究。Karkazis等人以风险和费用作为优化目标，建立多目标路径优化模型，用分支定界法进行验证求解。Jassbi等以运输距离、风险、事故率、风险暴露人数为目标，构建多目标优化模型，并采用遺传算法进行了求解。Fahad A1Rukaibi等在运用GIS基础上，引入扩散模型和碰撞模型，在不同的事故情景下分析事故的影响区域和严重程度，通过货物路由算法（DGRA）确定最佳安全路线。查伟雄等建立危险货物道路运输阻抗函数，并根据阻抗函数，建立了路径优化双层规划模型，用模拟退火算法对模型进行了求解H。宋伟程等考虑时间和季节情况影响，建立了点危险源评价模型，在估算毒害区域面积和事故损失的基础上，用传统模型结合最大最小模型进行求解。代存杰等根据路段在路网内的地理位置，设置总风险阈值和最小相异度约束，建立了多目标优化模型，并用遗传算法进行求解。

本文从危险品道路运输的多重属性出发，对道路运输网上各要素进行分析，并进行量化处理，建立危险品道路运输多目标函数，借助Matlab软件用Dijkstra算法和集成目标函数最优折衷路径的扩展标号法对危险品运输多目标优化模型进行求解。

1问题描述与分析

Stepl先求出和始发节点V1相连接的弧的运输成本、运输风险、运输时间的最小值。由以上数据可得到：与V1连接的最小值是0.220、0.136、0.145。

Step2用Dijkstm算法分别求得运输成本、运输风险、运输时间三个目标的最短路径，分别是①-③-⑥-⑧、①-③-⑥-⑤-⑧、①-②-⑤-⑧。

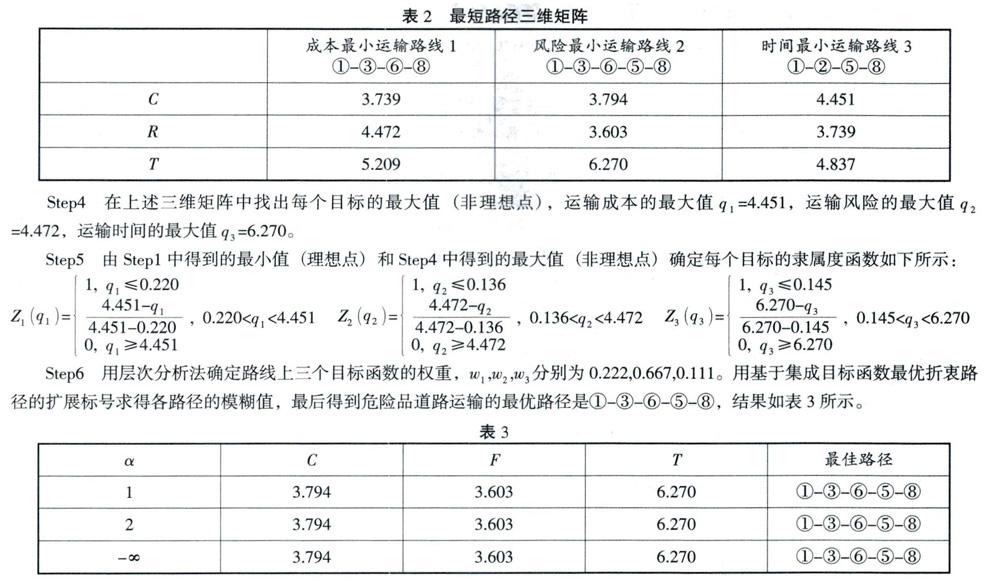
Step3计算上述每条运输目标最短路径的另外两个目标值，形成的三维矩阵如表2所示：

5结论

（1）本文从运输成本、运输风险值、运输时间三个运输目标角度对危险品道路运输路径进行优化分析，建立了确定环境下的道路运输多目标决策模型，使用模糊折衷规划算法进行求解，并应用实例来验证了模型的有效性和可操作性。

（2）本文采用扩展标号算法求解时不需要产生所有的Pareto最优解，只需找到一条决策者期望的Pareto最优折衷解，大大减少了工作量。

（3）本文在构建多目标决策模型时，未考虑时间不确定、风险不确定等不确定因素影响，关于不确定环境因素下危险品道路运输路径决策体系和路径优化方法有待进一步研究。