分布式并行遗传算法求解多车型车辆路径问题
2019-11-07王超袁杰红
王超 袁杰红

摘要:传统遗传算法在求解HVRP问题时寻优效率不高,在搜索过程中易陷入局部最优,发生早熟。为解决上述问题,文章在传统遗传算法的基础上,采用多个子算法并行分布、同时迭代的方式调整算法结构,并引入迁移算子实现迭代过程中各子算法间的信息共事,以提升寻优效率。
关键词:车辆路径问题;多车型车辆路径;迁移算子;并行遗传
在运筹学中,车辆路径问题(Vehicle Routing Problem,VRP)是经典的组合优化问题,已被证明具有NP计算复杂性,求解多采用近似算法和启发式算法㈣。遗传算法是模仿生物遗传过程的一种方法,每迭代一次既表示遗传一代,按照一定概率执行选择、交叉和变异算子,获得优良种群。传统遗传算法在求解VRP问题时容易陷入局部最优,所得近似最优解常不甚理想。本文采用分布式并行遗传算法,旨在提升算法搜索速度和寻优效果。
1多车型车辆路径问题模型建立
在上述模型中,公式(1)表示车辆不可超载,公式(2)表示车辆起止点均为配送中心,公式(3)表示所有客户均被服务,且任一客户仅由一辆车服务,公式(4)为0-1变量。 2分布式并行遗传算法设计
2.1算法介绍
分布式并行遗传算法(MDPGA)是在传统遗传算法(sGA)的基础上,依据分布式并行处理模型,对算法结构进行改变,以实现并行化操作。它将种群分成若干个子群并分配给各自对应的处理器,每个处理器独立的实现一个完整的串行遗传算法,并按迁移算子对子群体间的若干个体进行迁移,在引入优良个体的同时丰富了种群的多样性,有效避免了早熟现象的发生。
除遗传算子外,分布式并行遗传算法还引入了迁移算子,来负责各个分处理器之间的个体交换,以加速较好个体在各子种群中的传播。迁移算子主要考虑迁移规模、迁移拓扑和迁移策略三方面的内容。本文对迁移规模的确定主要依据经验,取子种群染色体数目的18%。迁移拓扑是指优良个体在子种群中的传播方式,本文采用一对多迁移方式。迁移策略主要是指迁移周期的确定,本文选择固定迁移周期。
2.2算法步骤
采用分布式并行遗传算法求解HVRP问题,算法步骤如下:
Step1:随机产生指定个体数目的3个初始种群作为并行算法的子种群;
Step2:若满足停止准则,输出结果;否则,转Step3;
step3:并行计算各子种群中个体的适应度;
Step4:采用轮盘赌方式并行执行各子算法的选择算子;
Step5:按交叉概率并行执行各子算法的交叉算子;
Step6:按变异概率并行执行各子算法的变异算子;
Step7:若满足迁移条件,执行迁移算子,转Step2,否则,转Step2。
2.3算法流程图
分布式并行遗传算法流程如图1所示:
3算例分析
3.1算例介绍
以16个客户的HVRP问题为例,配送中心编号为0,客户编号为1-16,节点信息见表1。车辆类型共有2种,其中,A型车2辆,限载量20t;B型车2辆,限载量10t。求车辆配送总里程最小的路径选择方案。
3.2算例求解
将车辆按限载量由小到大的顺序依次编号为1-5。分别采用基本遗传算法和分布式并行遗传算法求解,并行算法子种群数目设置为3,各子种群的规模均为10,交叉概率0.8,变异概率0.1,迁移周期为5,迁移规模为3,算法终止准则设置为迭代次数达到1000,所得最优路径结果如下:
路線1:0-8-6-2-5---0;用A型车;
路线2:0-7-1-4-3-0;用A型车;
路线3:0-9-10-16-14-0;用B型车;
路线4:0-12-11-15-13-0;用B型车。
最优路径如图2所示:
3.3算法对比分析
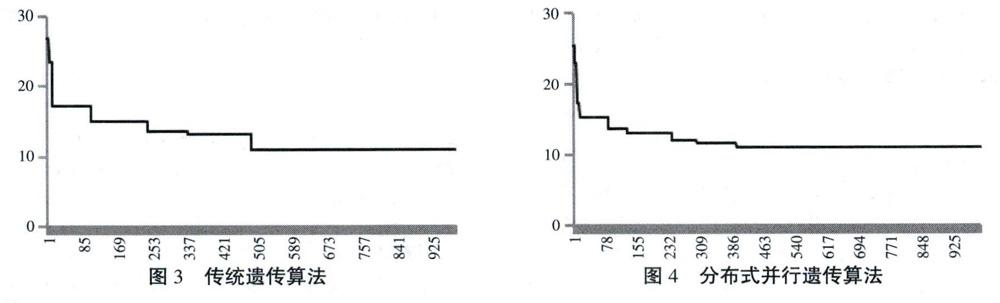
传统遗传算法与分布式并行遗传算法求解该HVRP问题的收敛图3、图4所示:
图3与图4比较后可知,MDPGA算法较SGA算法,收敛速度及鲁棒性都得到了很大的提升,有效避免了早熟,寻优能力增强,体现了MDPGA算法的优越性。
4结论
对比分析基本遗传算法(sGA)与分布式并行遗传算法(MDPGA)的收敛性可知,SGA算法的收敛性明显较差,在最优解搜索过程中,易陷入局部最优。MDPGA算法收敛速度较快,迁移算子使得算法全局搜索能力大幅提升。通过实例论证,分布式并行遗传算法在求解HVRP问题时收敛速度更快,具有更好地寻优能力,是一种更有效的算法。
