氢气-空气泄爆理论预测模型研究

韩森，沈致和，汪兴

（合肥工业大学土木与水利工程学院，安徽 合肥 230009）

1 引言

为了解决日益严重的能源危机和环境污染问题，迫切需要开发洁净、经济的新能源。氢具有燃烧无污染、效率高等优点，氢的利用等方面的研究被世界各国高度重视。截止2017年1月，全球已经有两百多个加氢站投入运营，相应的氢汽车也是逐年增加。然而氢气具有密度小、点火能量低、爆炸极限宽（4%～75%）、燃烧速度快等特点。一旦氢气储存和使用不当而发生泄漏，在外界点火源作用下可能会发生火灾甚至造成爆炸等灾害事故。而爆炸事故一旦发生，其损失是不可估量的。因此为了预防和减少事故发生的危害，迫切需要发展氢防爆抑爆技术。

泄爆作为一种最有效降低氢爆炸超压的方式，获得研究者大量关注，国内外开展了大量的实验研究和理论研究。郭进等人[1-5]在带有泄口面积为49的圆柱形小容器（V=12266cm3）中进行了不同工况下的实验研究，实验研究发现在同种泄口面积下，不同的氢气浓度、不同的点火位置（前、中、后）对最大超压的影响。Daubech等人[6]在2m×2m×1m的容器中，开展了泄口面积为0.5m2，不同点火位置、氢气浓度（10.5%～28.7%）等工况下氢气/空气爆炸实验研究。结果表明，容器内部产生最大超压明显受点火位置、氢气浓度等参数的影响。Bauwens等人[7-10]开展了大尺度舱室（4.6m×4.6m×3m）中氢气/空气的泄爆实验，针对不同的点火位置、不同泄口面积、低氢气浓度等参数下对爆炸超压进行了研究。Bauwens等人发现泄口面积对容器内部产生的峰值超压也有影响。Kumar等人[11]在超大型容器（V=120m3）中开展了泄口面积、氢气浓度、点火位置对爆炸压力的实验，发现对于给定的泄口面积，泄爆产生的最大峰值压力随氢气浓度的增加而增加，同时对于给定的氢气浓度，泄口面积越小，泄爆压力峰值越大。Rocourt等人[12]在体积为3357cm3的正方形小舱中进行了5种泄口面积的工况下的泄爆实验，发现泄爆压力随着泄口面积的减小而增大。

对于受限空间的氢气/空气泄爆理论计算也受到前人的研究。Molkov理论模型[13]是基于DOI数而建立的，而DOI数对于湍流布拉德利数计算具有重要的影响。该模型主要针对氢气浓度在30%以下的爆炸超压计算，其计算形式分为拟合计算公式和保守计算公式，该理论模型考虑了容器大小、障碍物、气体性质以及燃烧过程中气体变化特性等影响因素对于氢气/空气泄爆超压的影响。其中容器形状大小考虑了体积和泄口面积对于超压的影响。在有障碍物的情况下，该模型赋予了障碍物影响因子为3.5用于超压的计算，而没有障碍物时，障碍物因子取1。对于气体特性以及混合气体燃烧特性，考虑到气体膨胀系数、气体比热比以及各种褶皱火焰影响因子对于超压计算的影响。NFPA 68理论模型[14]主要是针对前人的实验结果而提出两种压力形式的计算模型，一种是针对静态低压，另一种针对静态高压。该模型明确了初始湍流、障碍物、容器形状大小、泄口面积、气体的燃烧过程变化的特性对泄爆超压的影响，但是没有分析点火位置对可燃气体爆炸超压的影响。在一般情况下，该理论模型计算的爆炸压力值要高于实验结果。Bauwens理论模型[7，15]是基于氢气/空气的混合气体在带有泄口的容器中泄爆产生的三个压力峰值进行理论计算。首先，Bauwens等人对每个压力峰值的形成机理进行探究：第一个压力峰值的形成是由于容器内部气体燃烧；第二个压力峰值的形成是由于障碍物的影响；第三个压力峰值的形成是由于容器内部气体通过泄口到达容器外部形成爆炸。容器内部爆炸产生的最大超压可以通过三个超压峰值比较而获得。该模型充分考虑了点火位置、障碍物、外部爆炸、容器的形状、泄口面积、气体燃烧特性以及火焰面积等因素对于泄爆超压计算的影响。就理论模型而言，很少有人关注泄爆理论模型对于泄爆超压预测的普适性。研究泄爆超压理论计算模型对氢容器、建筑以及管道等设施的安全预测具有重要的指导意义。

2 结果研究和讨论

为了探究NFPA、Bauwens、Molkov三种模型对于计算爆炸超压的普适性，本文从容器尺度出发，分别选择了郭进等人、Daubech等人和Bauwens等人的实验工况和超压值，如表1～3。然后，通过三种理论模型分别计算得到的最大压力与上述实验产生最大压力相比较，分别从定量上和定性上来确定哪种模型最适用。

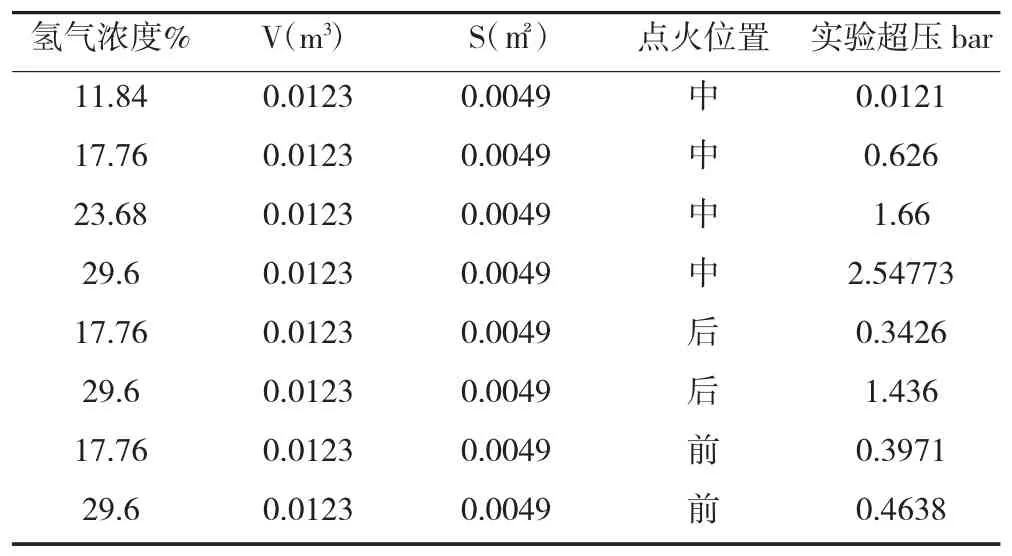
郭进等人 表1

Daubech等人[6]实验工况和超压 表2

图1给出了NFPA、Molkov、Bauwens三种模型计算出的结果与郭进等人的实验结果进行比较。从图1中可以看出，Molkov模型计算值明显低于实验值，并随着氢气浓度的增大，计算值与实验值的差距增大；NFPA和Bauwens模型计算结果非常接近于实验结果。此外，图1中还表明Bauwens模型计算结果更优于NFPA模型和Molkov模型的计算结果。因此，针对郭进等人的实验，Bauwens模型更适合于小型容器的爆炸超压计算。

图2给出了NFPA、Bauwens和Molkov三种模型计算值与Bauwens等人的实验值的比较。图2的结果表明；三种模型的计算结果都大于实验结果，且均偏离实验结果。通过图2中的对比可以发现；Bauwens和Molkov模型计算值更吻合实验值，且Bauwens模型计算值偏差最小。由此可见，针对Bauwens等人的实验舱，Bauwens模型优于其它两种模型。

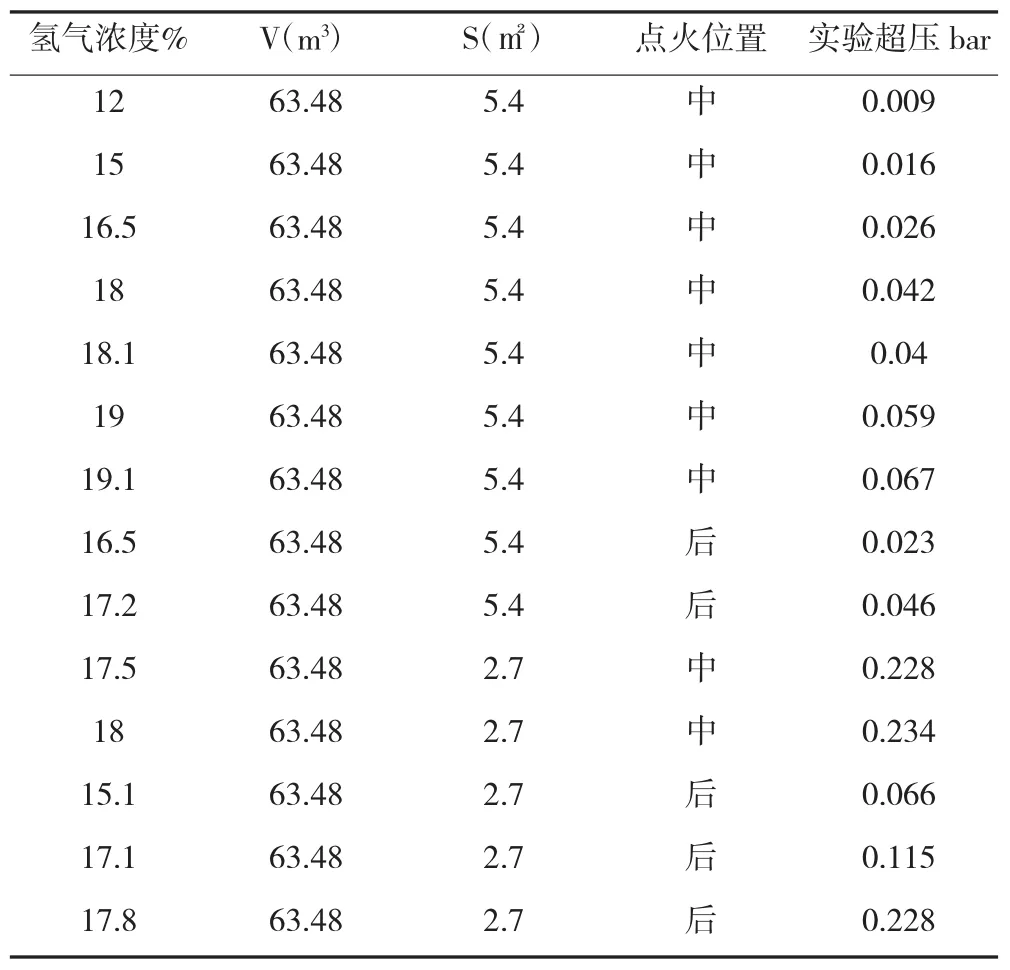
Bauwens等人 表3

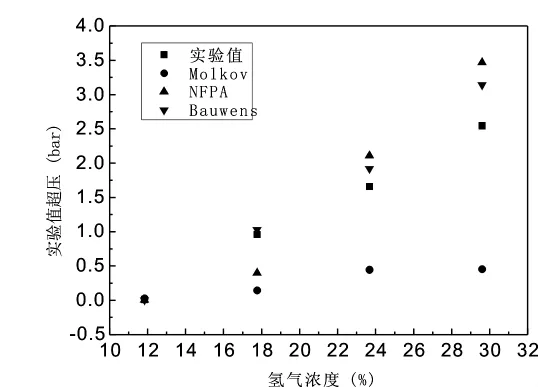
图1 三种模型计算值与郭进等人的实验结果对比

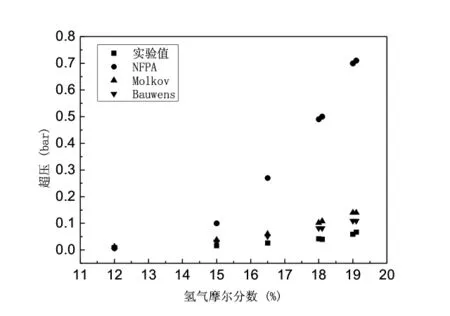
图2 三种模型计算值与Bauwens等人实验结果对比

图3 三种模型计算值与Daubech等人实验结果对比

图4 模型计算压力值与实验超压值对比

图3给出了三种模型计算值与Daubech等人的实验值比较。图3的结果显示，在氢气浓度为20%以内，Molkov模型计算值与实验值几乎相同，但是随着氢气浓度继续增加，其计算值偏离并小于实验结果。此外还发现，NFPA和Bauwens模型计算值随着氢气浓度的增加而增加，并且计算结果都大于实验值。整体来看，在中型容器中，Bauwens模型也优于Molkov和NFPA模型。

图4（a）～（d）给出了三种模型对所有工况的计算值与实验值之间对比。发现Bauwens模型计算值在45°线的上方区域并靠近45°线，即计算值略大于实验值。Molkov模型计算值占了整个区域，即计算值可能大于，也可能小于实验值，且偏差较大。NFPA模型计算值几乎都不小于实验值。图4（d）对比发现，相对于Bauwens模型计算值，NFPA模型计算值偏离实验值较大。

总的来说，对于受限空间中氢气/空气混合气体泄爆超压预测，Bauwens模型比Molkov和NFPA模型预测更准确。

3 结论

通过NFPA、Molkov和Bauwens三种理论预测模型计算的结果与实验结果比较，发现NFPA模型和Molkov模型的预测偏差最大，Bauwens模型更适合预测氢气-空气混合气体泄爆超压。因此，针对不同尺度的氢容器泄爆理论计算，建议采用Bauwens模型。