复变函数论中积分计算的教法研究

杨孝英

（长春工业大学，吉林 长春 130012）

关键字：复变函数积分；教学方法；教学实践

复变函数论作为数学学科的一个重要分支，在数学的其他分支（如微分方程、概率论）以及其他学科（如流体力学、理论物理）有着重要的应用。复变函数论已经成为理工科专业的一门重要的基础课程。复变函数的积分是复变函数论的主要内容之一。复变函数的积分是研究解析函数的一个重要工具，解析函数的很多性质都是通过复变函数的积分证明的。对于复变函数的积分的学习主要掌握两个方面：一是对复变函数积分的定义的理解；二是如何利用不同的积分计算公式来计算积分。

一、通过类比的方法深入的理解复变函数的积分

复变函数是高等数学的后续课程之一，在复变函数的教学过程中，通过和高等数学的相关知识点进行类比，找出相同点和不同点。不仅可以激发学生自主学习的热情还可以促进学生更好的理解复变函数的相关内容。分析比较这两门课程的内容之间的联系和不同，不仅可以为复变函数相关内容的学习提供参考，更重要的是，学生从比较中认真研究了复变函数的相关知识点。这样的教法思路和课堂教学方法真正达到了学生和教师的互动，提高了课堂教学效果。在复变函数的课堂教学过程中，教师可以把与本次课堂相关的高等数学的知识点作为复习内容，然后再引导学生学习复变函数的新的知识点，类比相同点，重点强调不同之处。例如，复变函数的极限的定义和单变量的实变函数极限的定义在形式上完全一致，这是相同点；而复变函数的极限要求变量沿着任意方向趋向与固定点的极限都存在且相同。显然复变函数极限的要求更高，这是与高等数学中极限概念的不同点。在教学过程中，重点指出这个不同点。这样做的主要目的是为了避免学生照搬高等数学的内容、理解错误等情况的发生。

从复变函数积分的定义来看，和实积分一样，都是分割、取近似值、求和、取极限的思路。复变函数的积分建立在复平面上，相当于两个二元的实积分，保持了实积分的大部分性质，如线性性、绝对值不等式、连续必可积等。而黎曼积分中的牛顿-莱布尼兹公式在复变函数积分中，只是对于解析函数在单连通区域上才成立。实函数的积分中值定理不能直接推广到复变函数的积分上来。在复变函数积分的计算方法上，解析函数的积分计算更加灵活多样。在课堂教学的过程中，通过与高等数学内容的类比，指出相同点，重点强调不同之处。充分调动学生的积极性，培养学生的自学能力。

二、合理的使用积分公式计算复变函数的积分

复变函数的积分一般通过以下几种方法来计算：1.积分的定义，化积分曲线为参数方程进而计算积分；2.牛顿-莱布尼兹公式；3.公式其中n 为正整数，c为以z0为圆心，r 为半径的圆周；4.柯西积分定理；5.复合闭路定理；6.柯西积分公式和高阶导数公式；7.留数定理。对于这些公式如何使用，具体的问题应该选择哪个公式来计算，这是学生经常提出的问题。

方法1 和方法2 一般是用来求解当积分曲线为不封闭曲线的积分。当被积函数解析并且很容易求出原函数的时候，使用方法2 计算积分，否则使用方法1。

当积分曲线为封闭曲线，一般使用方法3 至方法7 来计算。其中方法3 和方法4 是比较简单的情形，在计算复变函数积分时，首先判断是否满足这两种方法的条件，如果满足直接套用公式即可。如果不满足这两种方法的条件，我们进一步判断被积函数在积分曲线所围成的区域内部不解析点的个数。如果只有一个不解析点，考虑使用方法6；如果有多个不解析点，使用方法5 或者方法7。方法5 和方法7 有什么区别？如何判断使用哪个方法计算积分更简单？这是在复变函数积分教学中经常使学生感到困惑的地方。

如果被积函数具有或者可以化为形式：

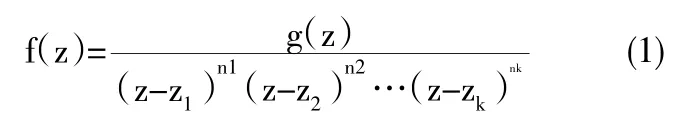
其中z1，z2，zk为被积函数f(z)在积分曲线c 的内部的不解析点，g(z)在曲线c 上及其内部是解析函数。此时选择使用方法5。例如计算积分，其中曲线c 为包含了0 和1的简单正向闭曲线。此问题由于被积函数的两个不解析点：0和1 都在积分曲线c 的内部，并且可化为形式?(1)。因此，在曲线c 的内部分别以0 和1 为圆心做两个互不相交也互不包含的正向圆周，然后使用方法5 计算该积分。此问题也可以利用方法7，先计算在不解析点处的留数，然后利用公式得到积分的值。

如果被积函数在积分曲线c 的内部有多个不解析点，但是不具有(1)的形式，使用方法7 计算积分。例如计算积分，被积函数在曲线│z│=5 内有四个不解析点，并且在这四个点处的留数都为-1，由方法7 可知，此积分的值为-8πi。因此，复变函数的积分计算可以选用不同的计算公式，在课堂教学过程中必须分析每个计算公式的适用范围，以及采用不同方法计算同一个复变函数积分的优劣。

三、利用Matlab 编程计算复变函数的积分

对于复变函数积分的计算，在理解了积分计算的理论知识之后，可以让学生将这些抽象的概念和繁琐的计算用Matlab 来实现。例如用留数定理来计算积分，此时直接调用Matlab 信号处理工具箱中的函数residue 来计算留数，进而计算积分的值。还可以用符号运算来编程计算。这么做不仅可以把复杂的复变函数的理论进行了教学实践，还可以激发学生学习这门课程的积极性，从而达到了更好的教学效果。