基于Kriging模型的齿轮副机构不确定性分析
2019-11-07巩博瑞陈虹旭殷国富
巩博瑞,陈虹旭,殷 鸣,殷国富*
(1.西北机电工程研究所,陕西 咸阳 712099;2.四川大学制造科学与工程学院, 四川 成都 610065)
乏组件水下检测装置是核电站中用来对乏组件进行测量的重要辅助设备,其稳定有效工作直接影响到核电站的安全运行。由于材料特性在统计上的离散性以及测量、加工、制造误差的存在,在地震工况下,装置薄弱部位会产生较大应力,且应力可能在较大范围内波动,因此有必要对其进行可靠性分析。对装置整机初步分析发现,装置中一对齿轮副属于薄弱部件,本文主要针对此齿轮副进行分析。
对地震工况下结构的响应研究,一般通过随机振动,采用概率与统计方法研究结构系统的动力响应,从能量角度分析激励的随机性问题[1]。目前随机振动分析[2-4]一般是基于有限元的,如:刘士华等[2]通过有限元软件分析了钢架结构在地震位移激励下的随机振动响应;马乾瑛等[4]对地震工况下的地铁车站结构进行了随机振动响应分析。进行可靠性分析的工程问题通常需要多次调用建立的有限元模型,而有限元模型一般为隐式函数,无法用确定的解析式表示,计算量较大,计算时间成本高,效率低。相较于蒙特卡罗法[5]、响应面法[6],Kriging模型[7-8]用较少的样本点就可以拟合出符合实际工程问题的代理模型,对于给定输入参数的预测也较准确,效率高。陈士诚等[7]基于Kriging模型对压力容器开孔接管区结构进行了可靠性分析,验证了Kriging模型在计算效率和精度上的优势。为实现对系统随机特性和风险水平的整体把握和完整认知,得到结构在各输入参数下的响应特性后,需要对结构输出响应进行概率密度函数估计。核密度估计是一种从数据样本本身出发研究数据分布特征的方法,采用平滑的峰值函数来拟合数据点,不需要数据分布形式,不附加任何假设,在统计领域有较大应用[9]。赵渊等[10]在大电网可靠性样本的基础上,通过非参数核密度估计实现了可靠性指标的概率密度估计,解决了传统期望值指标仅从概率平均意义角度测量系统的可靠性问题。
针对本文研究对象,笔者首先采用有限元软件ANSYS对齿轮副结构进行随机振动分析,得到其在地震工况下的响应,然后对随机振动分析中的关键参数通过多次有限元迭代,建立Kriging模型,最后结合不确定性变量与Kriging模型进行不确定性分析,计算结构失效概率并通过核密度估计得到结构随机振动响应概率密度曲线。
1 随机振动理论
当系统受到不能用时间的确定函数描述的激励作用时,产生的不确定性的振动过程称为随机振动,其分析一般是通过输入功率谱密度函数进行的。功率谱密度是随机动态载荷激励下系统响应的统计结果,是功率谱密度值与频率值的关系曲线。功率谱密度可以是位移功率谱密度、速度功率谱密度、加速度功率谱密度、力功率谱密度等[11-12],其定义为
(1)
式中:Sx(x)为激励信号的功率谱密度函数;Rxx(τ)为激励信号自相关函数;信号在时间间隔为τ的两数值之间的相互关系,用Rx(τ)表示。
(2)
当系统受到一平稳随机激励时,响应的功率谱密度可以表示为

(3)
式中H(ω)为传递函数。模态分析是随机振动分析的基础,通过模态分析,将机构固有频率、振型结果等作为随机振动分析输入,再通过随机振动分析,可得到分布在正态区间上的应力、应变值,从而为设计提供参考。
2 Kriging模型
Kriging模型是线性回归分析的一种改进技术,包含了线性回归部分和非参数部分[8],随机过程的实现取决于非参数部分,对于预近似的关于x多项式函数y(x)可以表示为
y(x)=F(β,x)+Z(x)=fTβ+Z
(4)
式中:f为x的多项式函数;β为回归系数;Z(x)为一均值为0、方差为σ2、协方差非零的统计过程,协方差可表示为
Cov[Z(xi),Z(xj)]=σ2R[(xi,xj)]
(5)
R(xi,xj)为样本点xi和xj的相关函数,通常采用Gaussian相关方程,形式为
(6)
式中θk和Pk为待定参数。对于任意点x,Kriging模型对y的预测为
(7)
其中r为待测点x和样本点间的相关向量,
r(x)=[R(x,x1),R(x,x2),…,R(x,xn)]
(8)
β*为极大似然估计因子,
β*=(FTR-1F)-1FTR-1Y
(9)
由此,可得Kriging模型对梯度dy/dx的预测值为
(10)
式中Jf(x)和Jr(x)分别为f和r的Jacobian矩阵。
3 核密度估计
分布密度能以曲线的形式直观表示可靠性指标围绕其平均值的变化趋势和变化程度,尾部特征可给出系统在严重风险下的信息,在实践中有重要应用价值。概率统计学基本问题之一是由给定样本点集合求解随机变量的分布密度,通常有参数法和非参数法2种。参数法需要提前确定样本的分布,由于分布种类较多,各分布特性相对单一,理论及实际应用表明采用该方法参数模型与实际物理模型差异较大,不能获得理想的分布函数[14]。核密度估计(kernel density estimation,KDE)是一种估计概率密度函数的非参数方法,由Rosenblatt和Parzen提出,其不利用数据分布的先验知识及概率分布形式的假设,对模型概率密度有很好的估计[10]。
设X1,X2,…,Xn,是满足概率密度为f(x)的总体X的样本,则其核概率密度估计定义为
(11)
式中:hn为窗宽;K(*)为核概率密度函数,通常选用以0为中心的对称单峰概率密度函数。为保证合理性,K(*)需满足:

(12)

(13)
其中σ为样本标准差。
4 齿轮副结构的有限元分析
有限元仿真分析可分为有限元模型建立、模态分析和随机振动分析3个过程。 本文采用UG建立三维模型,利用ANSYS软件Workbench模块进行有限元分析。
4.1 有限元模型建立
通过三维建模软件UG对联轴器、轴承、键等零部件进行删除、简化及合并,齿轮利用GC工具箱通过参数化方法建立,得到的三维模型由一对啮合的圆柱齿轮副及与齿轮配合的轴组成,倒角、细小孔、键槽特征被简化删除。
将简化模型导入Workbench,进行网格划分。材料属性如表1所示。

表1 材料属性
根据实际工作状况,将齿轮与轴约束设定为绑定接触,两齿轮之间约束设定为摩擦约束,检验并修改软件自动生成接触。网格划分对分析结果有较大影响,本次分析在软件自动划分的基础上,通过添加体尺寸策略、接触尺寸策略等对网格进行优化,网格划分结果如图1所示,共有6万6 622个节点,3万6 846个单元。

图1 齿轮副有限元模型
4.2 模态分析
模态分析是结构动力学分析的基础,通过其可得到结构的各阶固有频率及振型。通过功率谱密度函数可得到各模态下的模态响应幅值,各模态响应幅值叠加的结果就是随机振动分析的结构响应。根据齿轮副实际工况,在齿轮轴两端添加固定约束,分析得到结构各阶固有频率如表2所示,部分振型如图2所示。
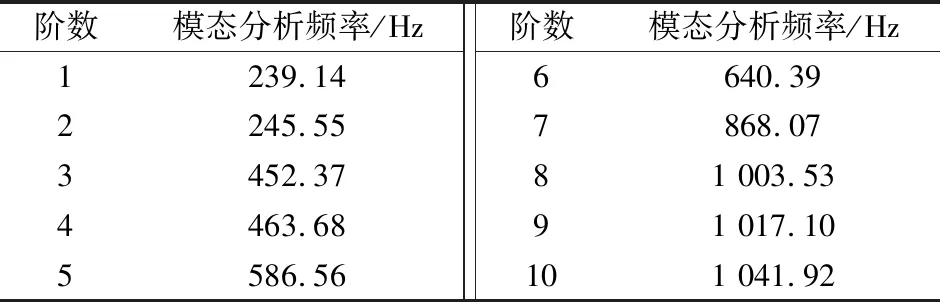
表2 模态分析结构各阶固有频率
4.3 随机振动分析
地震激励的加速度功率谱密度(PSD)如表3所示,将其施加在2个齿轮轴两端的固定约束处。选用模态为全部10阶频率,设定系统的阻尼比为2%。得到随机振动分析应力云图,如图3所示,其3σ应力为233.38 MPa,在齿轮轮齿啮合处最大,即在啮合位置处应力有99.73%的概率为233.38 MPa。

表3 加速度功率谱

(a)1阶振型
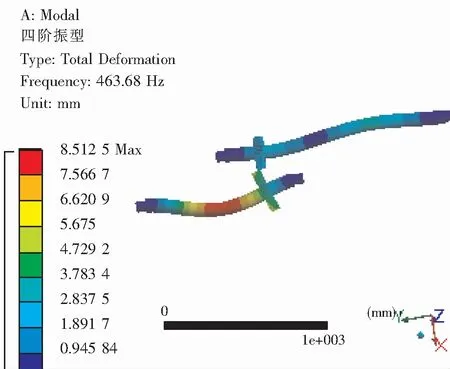
(b)4阶振型
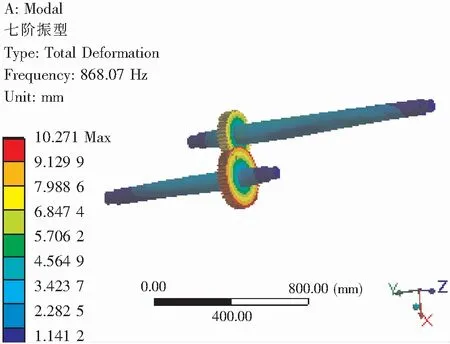
(c)7阶振型

(d)9阶振型


(a)齿轮副整体应力云图 (b)齿轮局部应力云图
5 基于代理模型的不确定性分析
由于代理模型与实际模型有一定的误差,传统基于代理模型的响应分析结果必然存在误差。有限元分析显示齿轮副啮合过程中应力较大,而且在实际工作过程中材料属性、零件尺寸参数、零件安装配合参数等变量都会产生波动,当各变量在特定组合时,有可能导致齿轮副应力过大,从而使齿轮结构发生破坏。
本文将代理模型随机振动下的3σ应力和参数不确定性相结合,通过Kriging建立代理模型,以有限元分析计算各不确定状态下响应,进而得到基于代理模型随机振动分析的可靠度,最后通过核密度函数得到结构输出响应的应力最大值的概率分布函数。不确定性分析流程如图4所示。

图4 不确定性分析流程
5.1 Kriging模型
本文以随机振动3σ应力为目标变量,以齿轮的轴半径r、峰值功率谱a(即100~1 000 Hz段功率谱)及轴弹性模量E为不确定性变量。假设各不确定性变量满足正态分布,为:
r~N(35,0.12)
a~N(0.02,0.22)
E~N(2×1011,0.12)
(14)
为满足精度要求、模型收敛条件并减小仿真计算量,根据齿轮的轴半径r、峰值功率谱a和轴材料的弹性模量E的分布参数,产生65组随机样本点(每组样本点包含1个轴半径r值、1个峰值功率谱a值和1个轴材料的弹性模量E的值),将每组样本点分别作为Workbench中有限元分析的模型参数,得到齿轮副结构随机振动的有限元计算3σ应力结果值。将65组样本点和对应的应力结果值作为Kriging模型的训练样本点,从而建立关于齿轮的轴半径、峰值功率谱密度、轴弹性模量与随机振动下3σ应力的Kriging模型。
5.2 失效概率计算
为计算结构的可靠性,需要预测各变量在随机波动下目标变量3σ应力。根据结构参数变量的分布特性,采用蒙特卡洛法生成106组样本点,代入建立的Kriging模型,预测各样本点下随机振动3σ应力值。
3σ应力可能失效功能函数g(x)为
g(x)=σs-σKriging
(15)
式中:σs为极限应力值,根据强度要求取380 MPa;σKriging为基于Kriging模型预测的3σ应力。齿轮副结构失效概率P的计算公式为
P=P(g(x)<0)=P(σs-σKriging<0)
(16)
5.1节建立了齿轮的轴半径、峰值功率谱密度、轴弹性模量与随机振动下 3σ应力的Kriging模型,基于此模型,可以采用传统的蒙特卡洛方法来求解3σ应力齿轮副结构的失效概率。具体的求解流程如下:
1)根据齿轮的轴半径r、峰值功率谱a和轴材料的弹性模量E的分布参数,随机产生N个输入样本点A;
2)将A代入5.2节建立的Kriging模型中,可得输出响应B(即3σ应力值,为N×1数组);
3)根据式(15)可得失效功能函数值C(为N×1数组);
4)统计数组C中小于零的项,总数记为M;
5)按式(17)计算失效概率。
(17)
计算得到齿轮副结构失效概率为 0.000 573 9,齿轮副结构在随机振动下失效概率低,可靠。
5.3 3σ应力概率密度估计
由Kriging模型预测得到106个随机振动3σ应力值,采用核密度估计,得到3σ应力值概率密度曲线,如图5所示。可以看出,3σ应力在[200,370]MPa区间内概率密度值较高,在区间两侧概率密度较低,分布情况与实际工程经验一致。

图5 概率密度曲线
6 结束语
1)对水下检测装置中一对齿轮副结构进行了多软件联合随机振动分析,仿真得到了该结构在地震激励功率谱下的响应。
2)考虑到各不确定性变量,对齿轮副结构进行基于代理模型的不确定性分析。通过建立的Kriging模型预测各随机状态下的随机振动3σ应力。计算得到的失效概率显示,该结构可靠度较高,可满足核电工作条件。
