A Correlation Coefficient Approach for Evaluation of Stiffness Degradation of Beams Under Moving Load
2019-11-07ThanhNguyenThaoNguyenHNguyenXuan45andNhiNgo
Thanh Q.NguyenThao T.D.NguyenH.Nguyen-Xuan45 and Nhi K.Ngo
Abstract:This paper presents a new approach using correlation and cross-correlation coefficients to evaluate the stiffness degradation of beams under moving load.The theoretical study of identifying defects by vibration methods showed that the traditional methods derived from the vibration measurement data have not met the needs of the actual issues.We show that the correlation coefficients allow us to evaluate the degree and the effectiveness of the defects on beams.At the same time,the cross-correlation model is the basis for determining the relative position of defects.The results of this study are experimentally conducted to confirm the relationship between the correlation coefficients and the existence of the defects.In particular,the manuscript shows that the sensitivity of the correlation coefficients and cross-correlation is much higher than the parameters such as changes in stiffness(EJ)and natural frequency values(Δf).This study suggests using the above parameters to evaluate the stiffness degradation of beams by vibration measurement data in practice.
Keywords:Correlation coefficient,cross-correlation,vibration signal,vibration amplitude,frequency.
1 Introduction
Studies related to identifying defects are frequently based on mechanical parameters like distinct frequencies,damping coefficients,vibration types,and shock coefficients.Distinct frequencies are one of the most popular parameters to be used in verifying bridges.When designing and building a bridge,the distinct frequencies are bigger than other forced vibration frequencies caused by environmental effects on the bridge such as winds,earthquakes,traffic vehicles,and so on.However,after several years,under the effects of aging materials as well as unforeseen environmental impacts,bridges are downgraded and their distinct frequencies are reduced.The unusual feature which is currently being used is a damping coefficient.The damping coefficient characterizes the energy loss of the mechanical system during vibration process.The main purpose of our method is to specify the energy loss of the structure during vibration which is examined by the overall technical structures through measurement data of external impact on the system.It is found that damping is more sensitive to stiffness decline than distinct frequencies.Therefore,there is a tendency to use damping for evaluation of the working condition of bridge's structures.In general,it is changes in mechanical properties of materials due to increase of damping,which directly relates to energy loss during vibration process.When a system loses too much energy during its vibration process,the destruction is taken place very quickly and vice versa.Consequently,Montal et al.[Montal,Ribeiro and Duarte-Silv(2009)].Montal suggested using damping as a useful and potential tool to identify defects.Zhang et al.[Zhang and Hartwig(2002)]showed that the damping coefficients are more sensitive than distinct frequencies in observing and evaluating the health condition of structure because changes in damping are greater than distinct frequencies.Similarly,Saravanos et al.[Saravanos and Hopkins(1996)]also conducted some experiments on many composite girders and found that delamination of materials has more effects on damping abilities than the distinct frequencies.Colakoglu[Colakoglu(2003)]stated that damping coefficients are directly proportional to the number of fatigue cycles,from which we can easily identify the hardness decline of the system through the effects of defects.However,finding correctly the damping coefficients pays still challenging and these damping coefficients are only determined through the graph of dimming vibration.It could be emphasized that not all vibrations can be gained dimming amplitude graph.Pham et al.[Pham,Nguyen and Ngo(2001)]claimed that damping coefficients which are practically determined based on mock-up bridges can cause errors.The possible reasons for those errors come from measurement process,and the inability of the signal segment of dimming damping during data processing.Therefore,although damping coefficients have significant contributions to identify defects,this value is much more functional than the previous distinct frequency value.The problem will pose significantly reliable results only when being carried out in simulation calculations or doing experiments in laboratories.Such results are greatly affected or no longer reliable when being conducted in real life situations,especially in those whose input conditions are contingent.
Another parameter that also characterizes the vibration process is mode shape.Finding this parameter is based on changes of different vibration types.When the structure has defects,it leads to change of its original shape during the vibration process.Theoretically,when a mechanical system vibrates,it generates different types of mode shapes in accordance with different distinct frequencies.According to the law of accumulation,when a mechanical system vibrates withndistinct frequencies,it createsnharmonic vibrations.Such aforementioned analysis is often called distinct mode shape analyzing method.This method is effectively used when we take it under the survey of forced vibration and evaluation of mechanical system's parameters[Salane,Baldwin and Duffield(1981)].This perspective has caught the attention of many researchers[Beck,Katafygiotics and Balkema(1992);Kaouk,Zimmerman and Kissimmee(1993)].It was stated that changes of mode shape are much more sensitive than distinct frequencies and damping coefficients.The mode shape identifies minor changes of defects through mockup bridges.The aforementioned results were almost focused on identifying defects by the vibration method.Such studies cover many issues relating to mode shape relating to mode shape,such as mode shape values and curvature,measured modal flexibility,uniform load surface curvature,unit load surface curvature as well as damage index method.Obviously,results from those studies are only sensitive when they are simulated on number imitation.By investigating 37 bridges in Ho Chi Minh City with many different bridges' forms including structures,materials,architecture,and operating time,we proved that changes in mode shape are not sensitive enough to identify defects in reality[Pham,Nguyen and Ngo(2001)].It can be explained by the fact that when practically trafficking with random load,the vibration on bridges is the combination of many component vibrations affecting system.Depending on changes in traffic,one mode shape can be more noticeable than others and vice versa.When occurring defects on mechanical systems,changes of these defects often affect mode shapes of vibration,accordingly.However,the nature of random vibration is the combination of many component vibrations and it scatters the changes of mode shape.According to Nguyen et al.[Lien,Duc and Khiem(2019);Khiem and Hang(2018)],the authors measured vibration parameters of plastic beams which have cracks.The study showed that change in mode shape is insignificant when cracks are created with their depth from 0 to 60%compared to the thickness of experiment beams,and changes in breaks make the fourth distinct frequency change.The level of changes in the fourth distinct frequency is also insignificant(less than 10%)compared to the time when it has no crack.Different mode shape parameters create minor level of changes which cannot be observed directly.However,the limitation of this study is that it only investigates the effects of existing cracks(which can be clearly seen by naked eyes).It,however,was not mentioned any micrometer defects due to the lack of appropriate facilities when conducting experiments,according to Rabczuk et al.[Rabczuk,Ren and Zhuang(2019);Anitescu(2019)].
In this work,we propose using correlation and cross-correlation coefficient models to assess the stiffness-deterioration of beam structures subjected to moving load.We then apply two aforementioned parameters to evaluate the status and damage level caused by defects.Firstly,the outcomes of using correlation coefficient aim to assess the extent and effect of defects on beam.Secondly,the cross-correlation model is basically used to determine the relative position of defects.Our experiments were carried out to affirm the relationship between correlation coefficient and the existence of defects.Furthermore,we compare the sensitivity of the correlation coefficient and cross-correlation parameters with either the parameter of changes in stiffness or the changes in frequency value.These values can be broadly applied to different structural systems as well as load bearing states.In fact,this correlation parameter was also applied in several previous studies on evaluation of the state of structures.However,to determine the correlation coefficient value,these applications are usually done by an intermediate transformation.These studies frequently determine correlation coefficients through some intermediate transformations such as the Fourier Transform,the Fast Fourier Transform,the Windowed Fourier Transform,the Wavelet Analysis(including both discrete Wavelet analysis and continuous Wavelet analysis).According to studies Zang et al.[Zang,Friswell and Imregun(2007);Pan,Qian,Xie et al.(2009)],the correlation coefficient has been applied between the two responses of natural frequencies through the Fourier transform.This is the main criterion used in evaluating the health conditions of bridges found in previous studies.With respect to these works,they used two parameters:the correlation of shape functions and the correlation of amplitude functions.In addition,through the numerical simulation,the value of this correlation function is defined in order to identify changes among elements(before and after having defects).Meanwhile,through the measured data collected from experiments,the finite element analysis for evaluation of the health conditions was then updated.Simultaneously,data are measured from experiment to re-update the initial finite element modeling.Then,Yang et al.[Yang,Yu and Sun(2007);Koh and Dyke(2007)]predicted the defects in structure by vector of autocorrelation function(cross-correlation)of vibration amplitude according to power spectrum.It was showed that under the act of random force with specific frequency,the cross correlation function amplitude vector-CorV only depended on the matrix function responding to the frequency of structure.It is also assumed that CorV is normalized with stable and specific shape during the whole investigation.However,the normalizing process made the signals become more insensitive and errors than the initial form.Applying numerical simulation,Farid[Farid(2011)]proposed the method of updating the finite element modeling to detect defects in structure by frequency measurement.Cumulative function for defects is established from the remainder of the curve of correlation function in frequency domain.Optimization algorithm was applied in solving relevant problems such as improving the quality of correlation function in jamming treatment.Therefore,when applying correlation coefficient to the above studies,researchers usually evaluated on the results of simulation or by the Fourier Transform,the Fast Fourier Transform,the Windowed Fourier Transform and the Wavelet Analysis.This is the reason explained for the shortcoming and low-sensitivity of the result in evaluating defect in structure.Accordingly,except the suggestion of applying correlation coefficient and cross-correlation to beams,the new prominent point of this research is to apply the original signal of mechanical system.The original signal contains more necessary information for the process of evaluating and detecting defects than the information observed by intermediate transformation.In addition,during the process of identifying the correlation coefficients through original signals,there is a requirement that the two data sets must have the same files and the same measurement period in the same condition.Therefore,all the measurement channels must be adjusted concurrently and uniformly(the number of files,the sampled time,the sampled frequencies)in the experimental process.This is a relatively difficult requirement during doing experiments in order to calculate the correlation coefficients.This explains why there are not many studies on such a parameter in experimental Lab as well as in practical applications.
2 Theoretical background of data process
In this section,we establish the relationship between statistic distribution rules and distribution characteristics of mechanical vibration systems.All parameters collected from vibration measurement signals of beams have defects.In the meantime,we also suggest correlation coefficients and cross-correlation models.This provides a foundation for investigating the damaging level of beams with defects as well as identifying their locations.
2.1 Distribution regulation
Normal distribution,which is called Gauss distribution,is an extremely important probability distribution in many fields.It is a distribution generation with similar overall shapes with different location parameters(average valueμ)and ratios(varianceσ 2).However,statistically,the standard normal distribution is frequently used.The normal standard distribution average is 0 and that of variance is 1.Normal standard distribution is also called a bell curve because the graph of probability density has the bell shape:
Random variableXhas its density function which is expanded Gauss functionf(x).From Fig.1,we can say thatXhas normal standard distribution and is symbolized asX~N(μ,σ 2).According to To[To(2007)],the distribution has a sin function in accordance with:


Figure 1:The graph of normal distribution
At that time,the kurtosis ofn(x,μ,σ)is a symmetric bell shape through a lineX=μ,this distribution is identified by varianceσ 2.The curve areaf(x)(more precisely 99.7% of the area)is almost distributed in the middle of the straight line(μ-3σ,μ+3σ).Therefore,to apply this distribution,a data set needs to have the same statistic distribution rules on the condition that sampling time and samples must be consistent.
2.2 Correlation model
2.2.1 Correlation coefficients
A correlation method is a technique to evaluate the relation levels among signal groups.In this paper,we use the Pearson's correlation coefficient.Statistically,to test the relation between two data groups,there are many formulas but the Pearson correlation coefficient has been extensively employed.This is one of the most sensitive measurement methods which is only used when there is a relation between two variables.Pearson's correlation coefficient[Sanlane,Baldwin and Duffield(1981)]also known as the bivariate correlation is a measurement of similarity between two variables X and Y.This variable,which has its value ranging from-1 to 1,shows the level of dependence among variables.The correlation coefficient is 1 when there is linear covariant correlation and-1 when there is a linear invert correlation.The nearer this correlation coefficient is to 1 and-1,the stronger the correlation between variables is.The correlation coefficient is calculated in terms of dividing the square by standard deviation which is defined as:

The formula can also be redefined as:

in whichCov(X,Y)is the covariance betweenXandY,andσXandσYand standard variance.The standard variance is the square root of variance which is identified fromnsamples as follows:

The covariance betweenXandYis:

Pearson's correlation coefficient is shown as follows:

2.2.2 Correlation matrix
Like correlation coefficients,cross-correlation matrix ofnrandom variablesX1….Xnof matrix rank in the size ofnxnis performed in terms ofcov(Xi,Xj).If moment variables are used for the correlation coefficient measurement,the correlation matrix would be similar to covariance matrix of random variables.

We have:

Likewise,the matrix of correlation coefficient is defined as follows:

As seen,the correlation matrix has symmetric quality.In this paper,we suggest widening the matrix model of cross-correlation of 4 measuring positions.The purpose is to examine changes in the relation among signals in the most general way.The correlation matrix model demonstrates the correlation among signals which is shown in Tab.1.

Table 1:Correlation matrix model[jxj]
The correlation matrix among 4 signals from 4 measuring channels is shown in Tab.2.
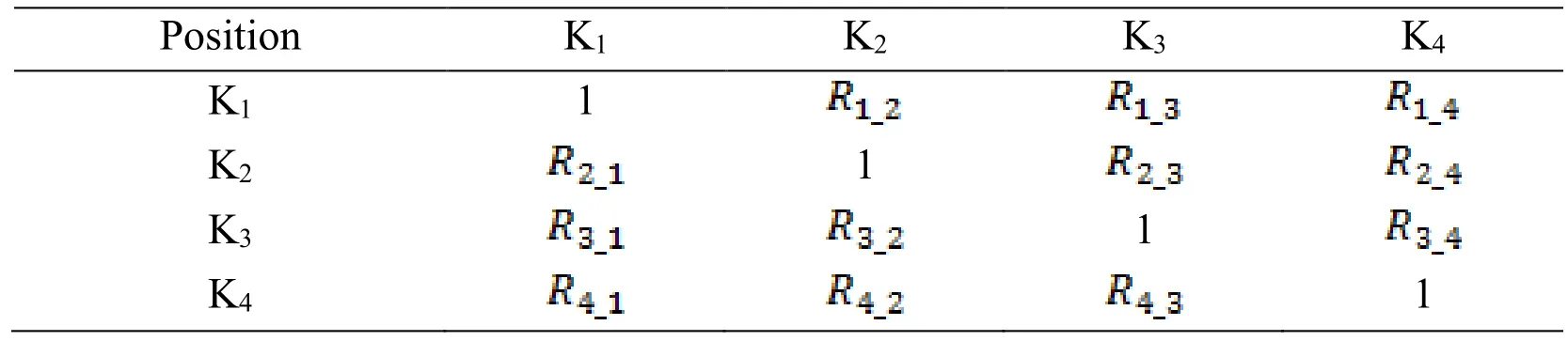
Table 2:Correlation matrix among 4 signals from 4 measuring channels
2.2.3 Relationship between correlation coefficient and detect structural damage
Consider a structure under a steady random excitation withnresponse-measuring nodes.The cross-correlation function both thekthresponsexk(t)and the lthresponsexl(t)is shown by

whereTis the duration of the template,and the cross-correlation is normalized with autocorrelation values for the given time.For each possible source locationk,a running cross-correlation is performed between the function templates for that source location and a moving load of the accelerometer.The cross-correlation between thek thfunction templatexikrecorded by thei -threceiver and the accelerometerxirecorded by the ith receiver is given by:

If damage occurs nearly thekthsource location,then Eq.(13)should peak at the correct time of the structural damage event with a value close to unity.On the other hand,if there are multiple damage locations,the stacked cross-correlation functions should each peak at the corresponding times

3 Experiment data
This experiment model was created at the Laboratory of Applied Mechanic,Ho Chi Minh City University of Technology(Fig.2),including 03 groups of equipment:the model group,excitation creating group,and signal receiving group.
Figure 2:Experimental layout
· The model group includes:a steel plate to stimulate the load-bearing beam with 0.9 m length,0.01 m width and 0.005 m height(see Tab.3).A steel beam is rest on two trimmer beams(see Fig.3(a)).Besides that,at each head of the testing beam,a deceleration part is designed to make the model more realistic.When a vehicle come from the outside,passes through the beam and finishes its movement,it shall not make the steel beam become tight.To stimulate complicated acting force on the testing beam,the research has installed 1 more thin homogeneous plate which creates eccentric vibration.This is so that this experiment can change not only the running velocity of vehicle passing though the testing beam but also the rotating velocity of the vehicle engine(see Fig.3(b)).

· Figure 3:Beam model and model simulating a vehicle passing though the beam of model group
· The excitation creating group is formed by a vehicle-driven system,including:1 engine driven by belt-drive system.This system drives the vehicle to run over the beam in one direction and at a steady velocity(see Fig.4(a)).When performing movement,the velocity of vehicle model is controlled by 2 inverter machines.These machines can change the rotating velocity of the engine and the running velocity of vehicle(cf.Fig.4(b)).

Figure 4:Transmission and inverter machine of Excitation creating group
· The signal receiving group is built to measure various kinds of parameter in this research,including:velocity signal,acceleration signal,deformation signal and transpositionmeter measurement signal.The transpositionmeter is directly attached to the middle point of the beam(see Fig.5(a)).For vibration signal,the experiment shall collect parameters from velocity and acceleration sensors.The experiment uses 4 acceleration sensors and 4 velocity sensors attached to the beam at 4 locations.The measurement points shall be distributed evenly on the beam(see Fig.5(b)).At each point,we shall arrange one velocity sensor and one acceleration sensor to simultaneously measure both signals.Finally,the deformation sensor shall be installed at the middle point of beam(see Fig.5(c)).

Figure 5:Sensors installed on testing beam

Table 3:Basic parameters of beams
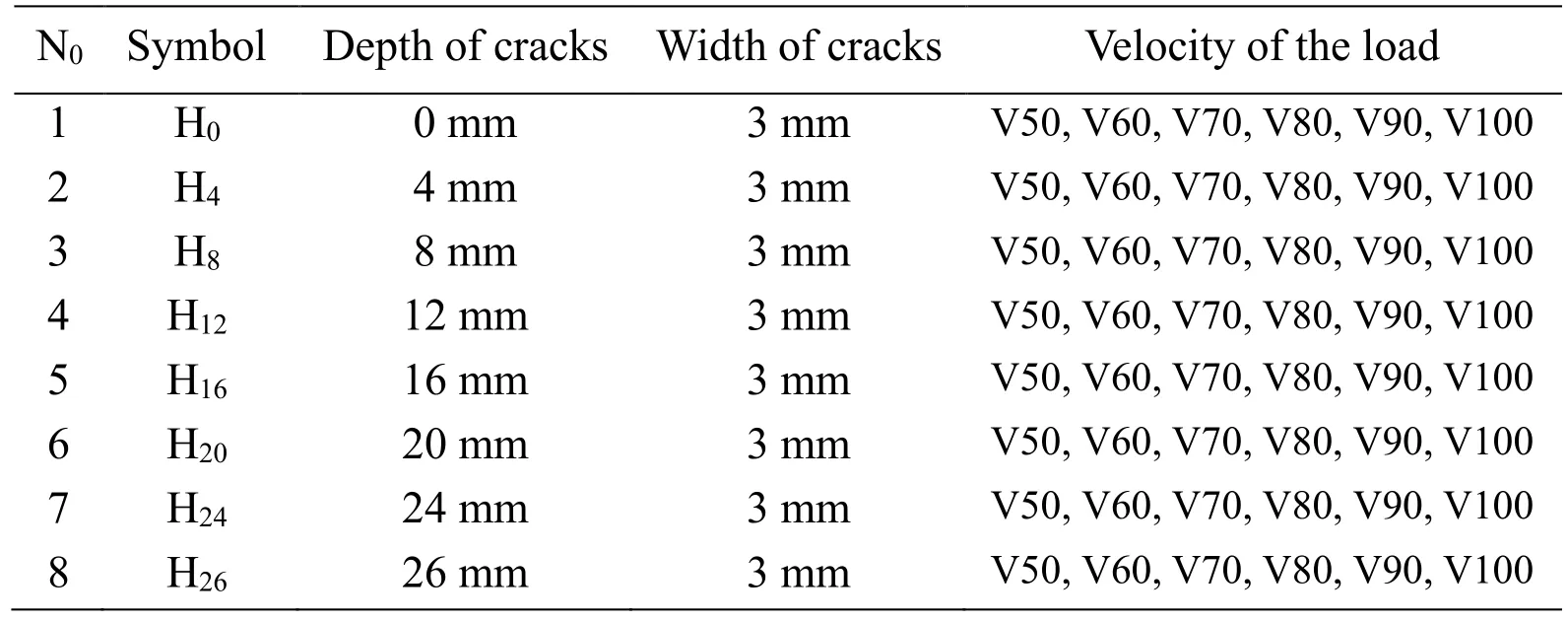
Table 4:Levels of cracks on beams
The experiment has been carried out in 4 different speed levels(V50=18.84 cm/s,V60=25,12 cm/s,V70=28.26 cm/s,V80=31.4 cm/s,V90=35.3 cm/s,V100=39.2 cm/s)of moving load which is shown in Tab.4 together with defects' levels.The moving load from left abutments to right ones on beams and sample parameters are shown in Tab.5.

Table 5:Signals' sample parameters
4 Results and discussion
4.1 Investigation the value of correlation coefficients
The experiment is conducted according to the following process:When we maneuver the moving load model through the experimental beams corresponding with different velocities from K1to K4,then the amplitude of the acceleration signal at 4 positions is shown in Figs.6-7.Beam without crack use V1=18.84 cm/s.Performing auto-correlation analysis to each data set at each position to evaluate the accuracy level from those data.

Figure 6: Original signal at 4 measuring positions without crack on beam
As a result,the correlated values between the measuring positions of signal set and the vibration amplitude obtained at corresponding sensor(K1,K2,K3,K4).These numbers are expressed on Figs.8-9,in which,the correlated values indicate the relationship between two data sets in the same state(same measured velocity and defect status).
From the correlation analysis for the above signal in the case with or without defects on beams,the results of correlation values are depicted in Fig.10.
It is shown that:
When a beam has no defect the correlation coefficient between positions is quite big,in which,the correlation coefficient between two consecutive measuring channels(R1,2,R3,4)reaches above 0.9,the one between two separated channels(R1,3)reaches above 0.7 and the two most distant channels(R1,4)reaches below 0.5.This fact indicates that during the process of vibrating beams caused by a moving load model,the amplitude of vibrating signal is divided into two parts:the first part is preserved in the process of propagating vibration at measuring points while the other one is altered by the time of propagating vibration or by friction causing energy loss.As a consequence,it leads to an incorrect process of propagating vibration among positions.Therefore,it reduces the correlation coefficient between measuring points significantly.
The correlation coefficient of two consecutive measuring channels(R1,2,R3,4)is above 0.9 which shows that it is very unlikely for the vibration from one channel to another to be measured incorrectly.Thus,the vibrating energy is almost conserved in H0(see Fig.10)for all consecutive measuring channels.However,this correlation coefficient depends considerably on the distance between two measuring points.Depending on this distance,the amplitude of vibration from one sensor to the other,which means that the vibrating energy also reduces.When the distance is far enough or affected by defects,the vibrating energy equals to zero in certain cases described in H4,H8,H12(see Fig.10).

Figure 10:The result of the correlation value according to the depth of the crack on the beam
When a beam is defected by a crack between measuring channel 2 and 3,it will leave a great impact on the correlation coefficient between these two channels under the same measuring state.The correlation coefficient between measuring channel 1 and 2(R1,2)dropped from 0.93 at the without having defect state H0to 0.79 at defecting state H12as during the process of propagating vibration,the instant energy loss at the defecting position diminishes the correlation coefficient among channels.This alteration happened because the vibration amplitude had to go through the crack to go from one to another channel in the same transmission direction.As shown in Fig.7,the correlation coefficient betweenK1andK3(R1,3)dropped from 0.73 at H0to 0.19 at H12(above 70% loss compared to the initial state).Same thing happened betweenK1andK4(R1,4)when their correlation coefficient went from 0.51 at the no defect state to-0.13 corresponding to the crack state H12(above 80% loss).Mathematically,the value of this parameter is in between[-1,1].However,when dealing with correlation coefficient in mechanical meaning,we only consider it from[0,1].This is a completely brand new feature of mathematical application in analyzing the meaning of mechanical vibration system.
When a beam has no defect,the correlation coefficient betweenK1andK2(R1,2)is nearly equal to that betweenK2,K3(R2,3)andK3,K4(R3,4)(which are 0.93,0.92,0.95 respectively).However,when there is a crack between channel K2and K3,the correlation coefficient between channelK1andK2is always much larger than that ofK2andK3with multiple defects and the more defects it has,the more significant the difference is.Hence,this is a sensitive parameter that can be used to identify the defects and their effect on the beams.
4.2 The relationship between the correlation coefficient and the growth of defects
Corresponding to each velocity,we carry out experiments with increased level of crack from H0to H26on different beams(from no crack to when the crack is big enough to destroy the beam).Analyzing the cross-correlation model(Rj,i)corresponding to following channels:(R1-i),(R2-i),(R3-i),(R4-i)to evaluate the overall relationship between the cross-correlation coefficient and the growth of cracks.We conduct different experiments on beams with cracks at different velocities of the moving load according to Tab.4.The result of each channel,as shown in Figs.8-11 represents the change of the correlation coefficient corresponding to every velocity,each state of defect and different channels(from channel 1 to 4).
The results from Figs.11-14 show that:
The correlation coefficient(R1,1,R2,2,R3,3,R4,4)at each measuring point is unchanged corresponding to different defected states.It means that at each measuring point,the relative energy is unchangeable.This is the foundation to assert the energy loss during the process of propagating vibration of beams.In other words,when two positions overlap one another,they have the same vibration energy.The more significant the distance between two positions are,the more energy loss,and vice versa.Therefore,with respect to the correlation at different overlapped positions,the correlation coefficients are always 1.In addition,they will be 0 when vibration transmission energy does not exist at these two investigated positions.In other words,in terms of mechanics,the correlation coefficients have their own values ranging from 0 to 1,which is totally different from that the mathematical aspect.
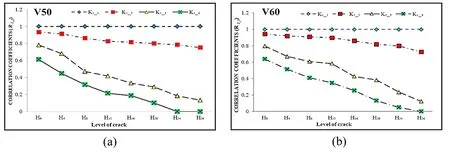

Figure 11:Relationship between velocity V50,V60,V70,V80,V90,V100 and crack levels of channel 1

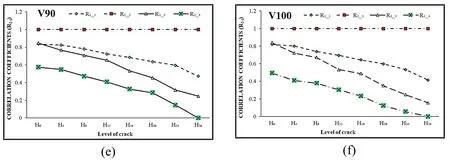
Figure 12:Relationship between velocity V50,V60,V70,V80,V90,V100 and crack levels of channel 2

Figure 13:Relationship between velocity V50,V60,V70,V80,V90,V100 and crack levels of channel 3
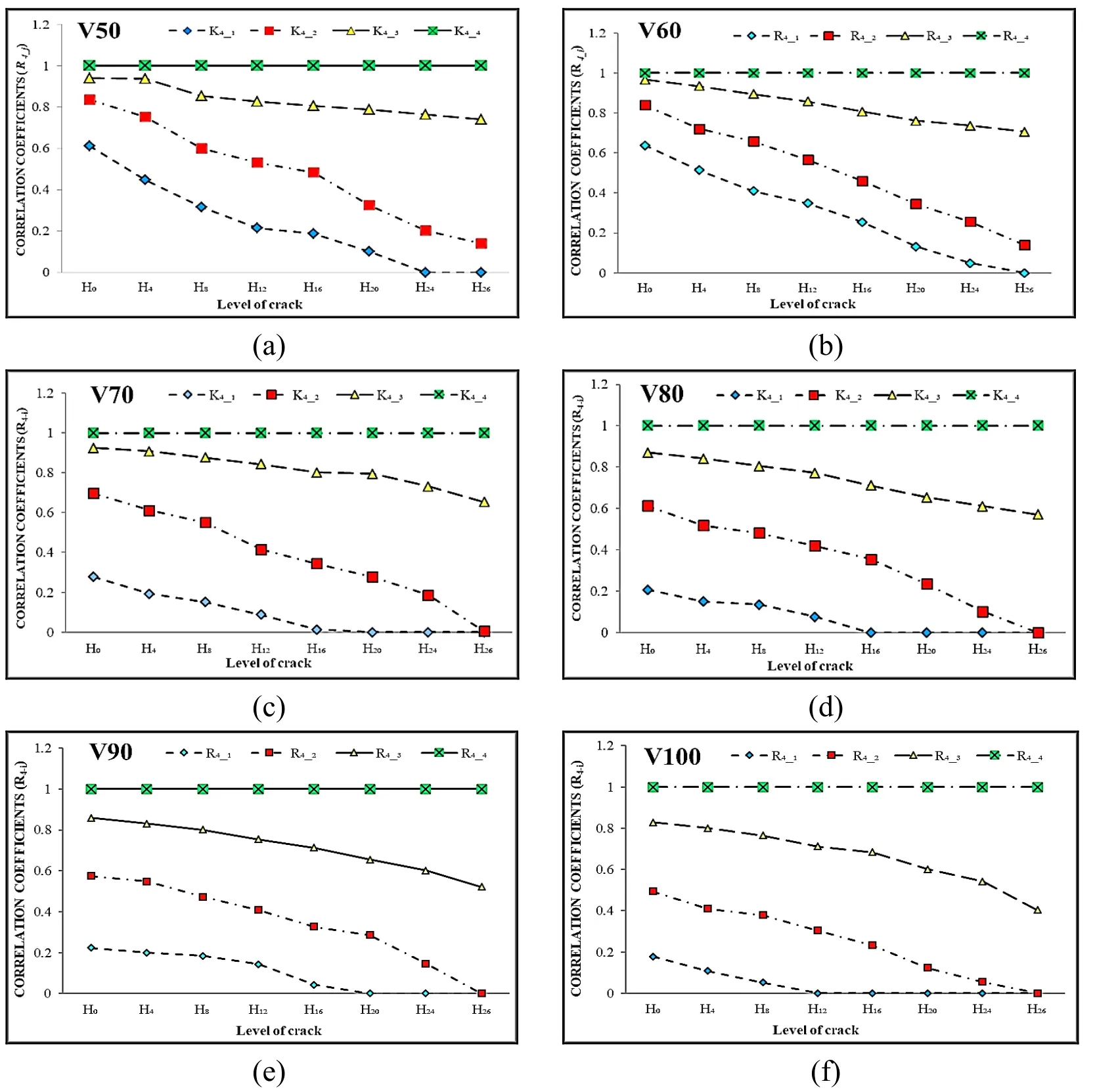
Figure 14:Relationship between velocity V50,V60,V70,V80,V90,V100 and crack levels of channel 4
The value of the correlation coefficient between two consecutive measuring channels(R1_2,R2_3,R3_4)is usually unchanged according to the direction of vibrating transmission as observed from Figs.15-16.Given the correlation coefficient observed at Figs.15-16,if two consecutive measuring channels have no crack in between(R1_2,R3_4),the correlation coefficient would be mostly constant.Thus,the distance between measuring points on the experimental beams is not broad enough to alter the correlation coefficient.However,when two channels whose positions have a crack(R2_3),this parameter goes down quickly at different states of the crack.The reduction rate of correlation coefficient changes according to the growth of cracks when compared with no crack state.Whilst,the correlation coefficient between two channels with and without crack changed drastically during the experiment.This is the basis to identify and evaluate defects on beams through the change of the correlation coefficient.This means that the correlation coefficient values are much more sensitive compared to the natural frequency values[Lien,Duc and Khiem(2019);Khiem and Hang(2018)]or mode-shapes[Spyrakos,Chen and Govidar(1990);Mazurek and DeWolf(1990);Pearson(1895)]towards beam models having cracks.

Figure 15:Relationship between velocity and crack levels on the correlation coefficient of channel 1,2(R1_2)
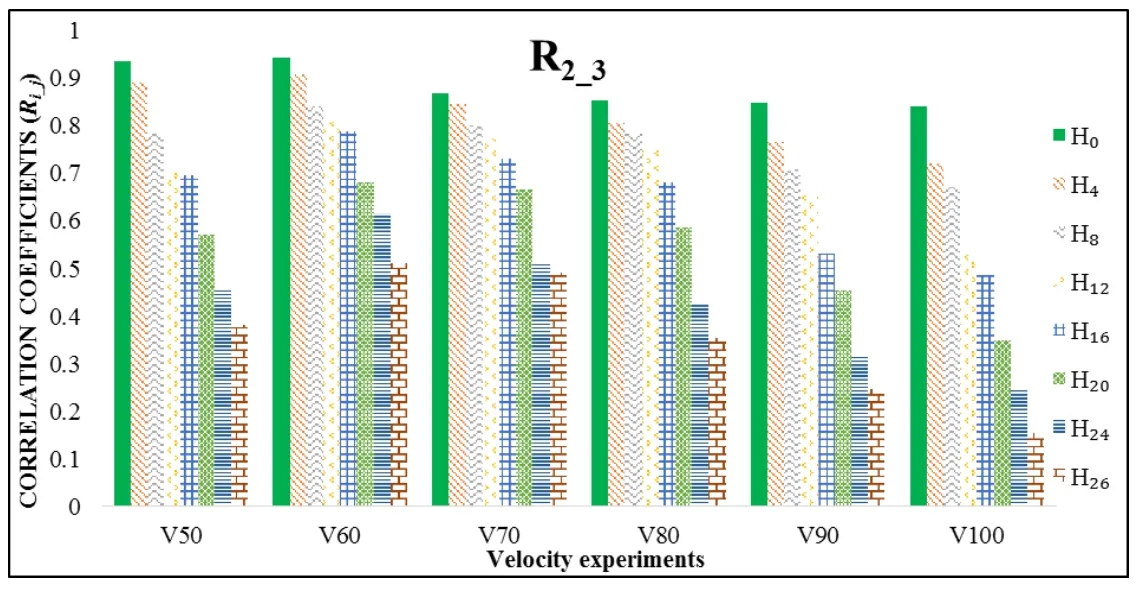
Figure 16: Relationship between velocity and crack levels on the correlation coefficient of channel 2,3(R2_3)

Figure 17:Relationship between velocity and crack levels on the correlation coefficient of channel 3,4(R3_4)
Given the effect of the velocity of the moving load on the experimental beams,the correlation coefficient will progressively increase as we increase the velocity in the experiment.As shown in Figs.18-23,the correlation coefficient is affected by the velocity and the level of growth of the cracks.Thus,this parameter is not just influenced by the location of measuring points but also the velocity of the moving load on beams.Figs.18-23 also show that the relationship between the velocity and the growth of cracks on the beam affects the value of this parameter.The velocity changes quickly and clearly in each state of the defect.

Figure 18:Effect of velocity experiment V50 on correlation coefficients in each crack levels
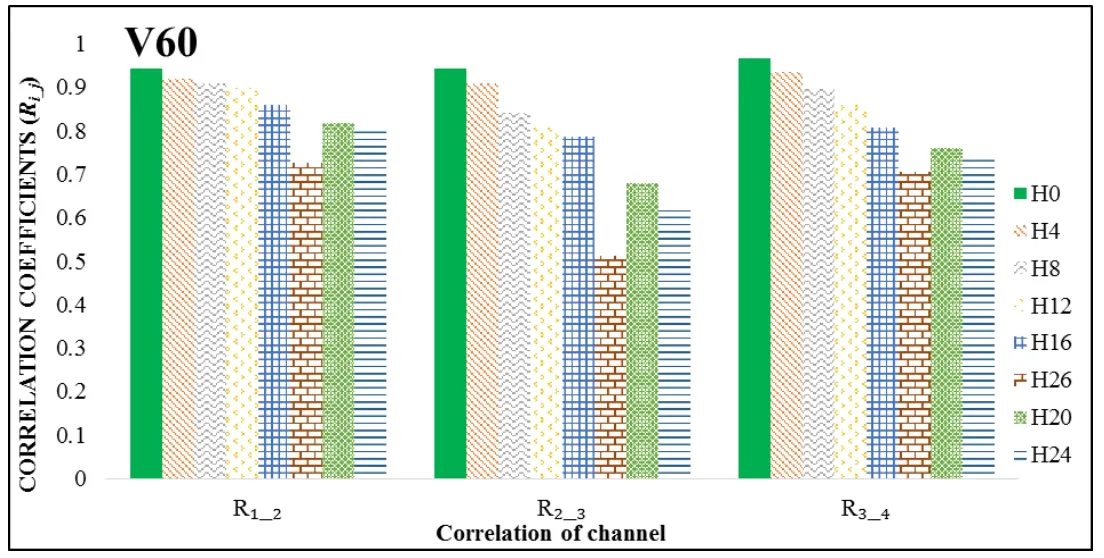
Figure 19:Effect of velocity experiment V60 on correlation coefficients in each crack levels
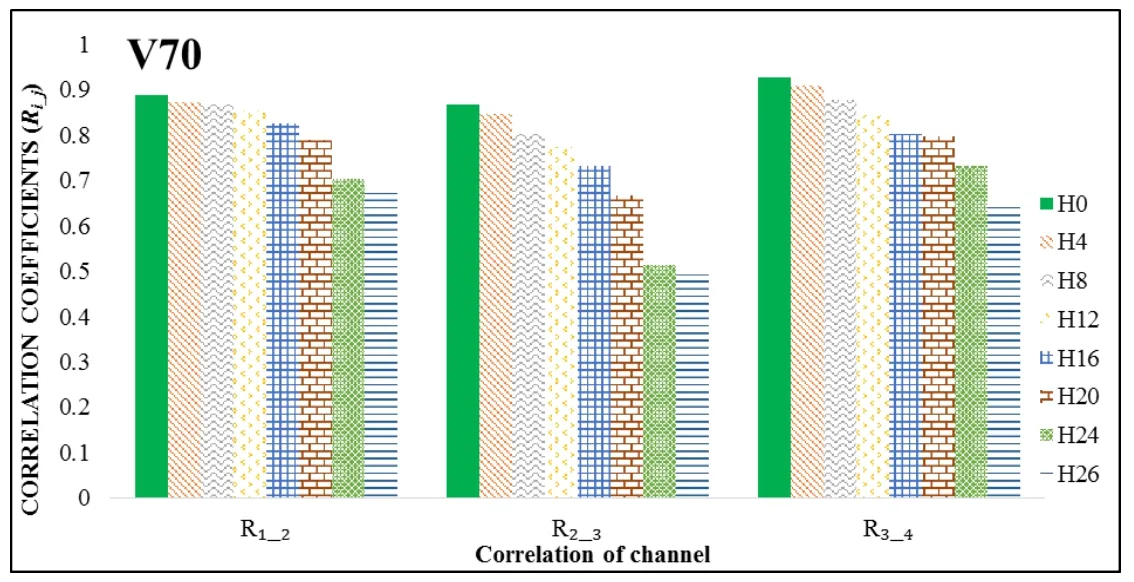
Figure 20:Effect of velocity experiment V70 on correlation coefficients in each crack levels

Figure 21:Effect of velocity experiment V80 on correlation coefficients in each crack levels
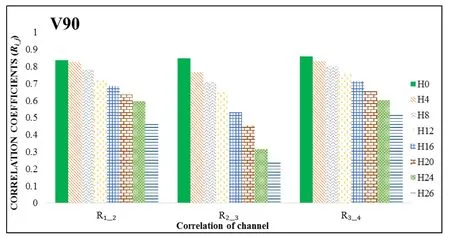
Figure 22:Effect of velocity experiment V90 on correlation coefficients in each crack levels

Figure 23:Effect of velocity experiment V100 on correlation coefficients in each crack levels
When the experimental velocity progressively increases,the correlation coefficient between two separated channels will change drastically.In other words,this parameter does not just depend on the velocity but also on the distance between two measuring points.Figs.24-26 show the relationship of the velocity and the alteration of the correlation coefficient between two separated channels with and without cracks.It is clearly seen that the vibrating energy was not conserved,which means the correlation coefficient changes at almost every state of the defect.

Figure 24:Relationship between velocity and crack levels on the correlation coefficient of channel 1,3(R1_3)

Figure 25:Relationship between velocity and crack levels on the correlation coefficient of channel 2,4(R2_4)

Figure 26:Relationship between velocity and crack levels on the correlation coefficient of channel 1,4(R1_4)
4.3 The sensitivity of correlation coefficient with a reduced bearing capacity of beams
We analyze the correlation coefficient of the vibration amplitude at the measuring points of every pair of sensor:K1andK2(R1_2),K1andK3(R1_3),K1andK4(R1_4),K2andK3(R2_3),K2and K4(R2_4),K3and K4(R3_4).The experiments are performed at different kinds of velocity and level of defects.The results will be compared simultaneously with both the change of the natural frequency value(Δ_f)and the change of the degradation of stiffness(Δ_EJ)at different states of cracks.This work aims to evaluate the sensitivity between the correlation coefficient and other parameters corresponding with the increasing level of defects.
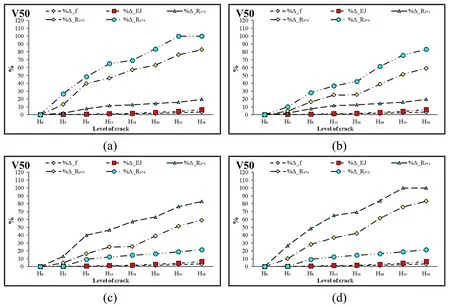
Figure 27:Compare the change of the correlation coefficient,natural frequency and decline overall stiffness at velocity experiments V50


Figure 28:Compare the change of the correlation coefficient,natural frequency and decline overall stiffness at velocity experiments V60

Figure 29:Compare the change of the correlation coefficient,natural frequency and decline overall stiffness at velocity experiments V70
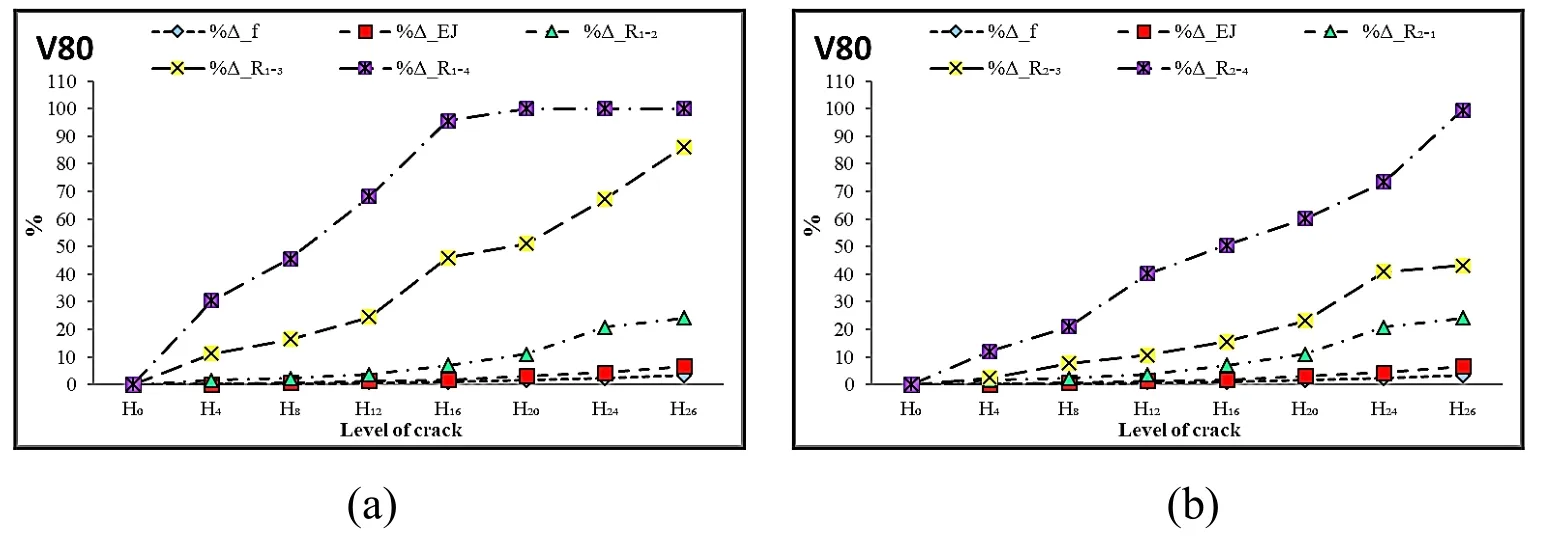

Figure 31:Compare the change of the correlation coefficient,natural frequency and decline overall stiffness at velocity experiments V90
It is observed that:
As seen in Figs.27-31,among the analyzing measurements,the natural frequency value of the experimental beams exhibits small changes.Therefore,in the experimental model of beams' cracks,the natural frequency value is not sensitive enough to detect and identify any cracks.This parameter is often used in many types in Lien et al.[Lien,Duc and Khiem(2019);Khiem and Hang(2018)],but,apparently,it is not accurate enough to solve the problems of identification and diagnosis damage in structures.
Similar to the natural frequency value,although the change in overall stiffness level is more sensitive than the natural frequency value,it is still insufficient compared to the growth of cracks.When a beam is at state H26,which means the depth of the crack is more than 70% of the thickness of the beam,the value of the change in overall stiffness level is below 7%,just like the experiment by Lien et al.[Lien,Duc and Khiem(2019);Khiem and Hang(2018)].Hence,we need to use parameters that are far more sensitive to diagnose and identify defects precisely.Specifically,that parameter must have the ability to identify cracks on the experimental beam.
Figs.27-31 also show the change in the correlated value between two vibration signals from the acceleration sensor at 8 levels of the crack with 4 levels of velocity(V50,V60,V70,V80).Accordingly,the correlation coefficients atR1_1,R2_2,R3_3,R4_4are the correlation coefficients of themselves with every level of cracks.This value gradually decreases at different channels and it will drop the most when two channels are at the furthest position(R1_4),which is also affected by the increasing depth of the crack.The change of this correlation coefficient increases in a linear way with respect to every velocity.The faster the experimental velocity is,the more significant the change is.,when the crack is big enough,with the depth betweenH12=12 mm andH26=26 mm(larger than 70% of a beams' thickness),this correlation coefficient changes immensely and is no longer linear compared to smaller cracks.In other words,these states of defects have affected the experimental beam considerably while the change in natural frequency value and overall stiffness is totally undetected.These results are quite realistic,in this level of depth,and the reaction of the beam has not been intact in comparison to the without having defect state.
5 Conclusion
This article investigated using the correlation and cross-correlation coefficients to evaluate the reduction of stiffness of beam under moving load.By proposing utilizing the original signals as the foundation for evaluating the correlation between two vibration signal datasets,this study has fully proved that constructing the correlation models through original signals is much more effective than other previous studies.This is due to the fact that such original signals are capable of storing the most important information of structures.These information sets are not blocked by values that are beyond the threshold or cutoff threshold of such intermediate transformations.Correlation coefficient value established by original signal is a sensitive parameter not only in determining the level of defect but also the relative location of crack on beam.In order to evaluate the sensitive of this new parameter,this research has compared it with the changes of natural frequency(Δ_f)and the changes in overall stiffness(Δ_EJ).Results showed the changes of natural frequency value(Δ_f)and overall stiffness(Δ_EJ)are not sensitive enough to evaluate the changes in structure(crack on beam).However,the changes of correlation coefficient value are more sensitive than the crack propagation in beam.This shows that we are able to widely apply this parameter into practice because it can be used for not only beam structures but also for other similar ones including:plates,bars,frames.This application will make a great contribution to reducing the calculating time compared to simulations,significantly reducing the actual inspection costs and be much more effective than other previous methods.In the future,this research shall be the premise for an effectively and practically appliance of these proposed parameters to evaluate the reduction in stiffness of beam by vibration measurement data.In the upcoming researches,we shall practically apply these parameters in bridge construction in order to monitor and forecast the deterioration of the works.
杂志排行
Computers Materials&Continua的其它文章
- A Heterogeneous Virtual Machines Resource Allocation Scheme in Slices Architecture of 5G Edge Datacenter
- Multiple Kernel Clustering Based on Self-Weighted Local Kernel Alignment
- A Physical Layer Algorithm for Estimation of Number of Tags in UHF RFID Anti-Collision Design
- A Compensation Controller Based on a Nonlinear Wavelet Neural Network for Continuous Material Processing Operations
- A Robust Zero-Watermarking Based on SIFT-DCT for Medical Images in the Encrypted Domain
- Bus Priority Control for Dynamic Exclusive Bus Lane
