A Compensation Controller Based on a Nonlinear Wavelet Neural Network for Continuous Material Processing Operations

Chen Shen,Youping ChenBing Chen and Jingming Xie

Abstract:Continuous material processing operations like printing and textiles manufacturing are conducted under highly variable conditions due to changes in the environment and/or in the materials being processed.As such,the processing parameters require robust real-time adjustment appropriate to the conditions of a nonlinear system.This paper addresses this issue by presenting a hybrid feedforward-feedback nonlinear model predictive controller for continuous material processing operations.The adaptive feedback control strategy of the controller augments the standard feedforward control to ensure improved robustness and compensation for environmental disturbances and/or parameter uncertainties.Thus,the controller can reduce the need for manual adjustments.The controller applies nonlinear generalized predictive control to generate an adaptive control signal for attaining robust performance.A wavelet-based neural network model is adopted as the prediction model with high prediction precision and time-frequency localization characteristics.Online training is utilized to predict uncertain system dynamics by tuning the wavelet neural network parameters and the controller parameters adaptively.The performance of the controller algorithm is verified by both simulation,and in a real-time practical application involving a single-input single-output double-zone sliver drafting system used in textiles manufacturing.Both the simulation and practical results demonstrate an excellent control performance in terms of the mean thickness and coefficient of variation of output slivers,which verifies the effectiveness of this approach in improving the long-term uniformity of slivers.

Keywords:Continuous material processing,wavelet neural network(WNN),nonlinear generalized predictive control(NGPC),auto-leveling system.

1 Introduction

Textiles manufacturing,printing,and other continuous material processing operations involve essentially nonlinear dynamic systems with coupling between the multiple inputs and multiple outputs of the manifold physical process[Valenzuela Bentley and Lorenz(2004);Tsakalis,Dash,Green et al.(2002);Djiev(2016);Moghassem and Fallahpour(2011)].These processing operations differ significantly from metal cutting processing operations according to two primary features.First,the materials being processed(e.g.,cotton,paper,and polymer films)are handled by multiple processing units that must maintain a high level of mechanical synchronization.For example,slivers are spun into yarn after several times of drawing,and the multicolor printing of paper requires multiple printing operations with precise registration and post-processing.Second,the quality of the end product is not only related to the precise control of processing units(e.g.,sliver drafting motors and roller printing motors),but also depends on the continuous physical processes applied to materials,such as fiber drawing processes and the application of tension to paper materials in printing processes.Moreover,these physical processes are closely related to the material characteristics and numerous external environmental factors.Thus,the quality of the final product cannot be assured by simply improving the control precision of processing units.Meanwhile,manual adjustments are unavoidable for addressing these changes in external and internal conditions.

The issue of control system robustness has been addressed by the development of many control strategies.For example,generalized predictive control(GPC),which was proposed in the 1980's[Clarke,Mohtadi and Tuffs(1987)],has been one of the most frequently used model-based control methods adopted in industry[Camacho and Bordons(1999);Low and Cao(2008)].In most GPC applications,linear models are employed to predict plant behavior over the prediction horizon,and to evaluate future sequences of control signals.Nevertheless,controllers based on linear models perform poorly when applied to nonlinear systems that operate over a wide range of operating conditions like continuous material processing systems.In this respect,numerous studies have analyzed the feasibility of GPC for the modeling and control of nonlinear system dynamic[Gu and Hu(2002)].For example,nonlinear GPC(NGPC)models have been developed successfully using conventional network structures such as artificial neural networks(ANNs),which have been shown to be capable of approximating a wide range of nonlinear functions to any desired degree of accuracy under specified conditions[Geng and Geary(1997);Hamdia,Lahmer,Nguyen-Thoi et al.(2015)].The neural network and hybrid regression models are applied in material design and producing field[Badawy,Msekh,Hamdia et al.(2017);Faizollahzadeh Ardabili,Najafi,Alizamir et al.(2018);Fardad,Najafi,Ardabili et al.(2018)].In addition,wavelets have been incorporated with ANNs to develop wavelet neural networks(WNNs)that combine the capability of ANNs to learn from processes together with the high resolution of wavelet decomposition[Delyon,Juditsky and Benveniste(1995);Chen and Hsiao(1999)].Here,the second layer of a WNN employs a wavelet transform rather than a standard activation function like the sigmoid function employed in conventional ANNs.The use of the wavelet transform allows for exceptional localization in the time domain via translation of the mother wavelet(a shifting process)and also in the frequency domain via dilation of the mother wavelet(a scaling process).Moreover,this time localization capability in particular readily lends the use of wavelet transforms to non-stationary signal analysis.Thus,the structure of WNNs have been demonstrated to provide greater potential than conventional ANNs for enriching the mapping relationships between inputs and outputs[Delyon,Juditsky and Benveniste(1995)].As such,WNNs are ideally suited for the modeling and control of dynamic systems[Billings and Wei(2005);Lu(2009);Abiyev and Kaynak(2008);Sureshbabu and Farrell(1999)].In addition,the training algorithms adopted for WNNs typically converge in a fewer number of iterations than those adopted for conventional ANNs.However,the standard feedforward network structure of WNNs is not the most suitable for solving temporal problems like predicting the behaviors of complex chaotic systems.To address this issue,Yoo et al.[Yoo,Park and Choi(2005)]developed a self-recurrent wavelet neural network(SRWNN)that combined the attractor dynamics of a recurrent neural network(RNN)with the rapid convergence of a WNN.Based on SRWNN,they developed a GPC for stable path tracking of mobile robots[Yoo,Choi and Park(2006)].Lu[Lu(2009)]proposed a stable predictive controller(SPC)for a class of nonlinear discrete time system using GPC with recurrent WNN(RWNN)model.This type of controller has its simplicity in parallelism to conventional GPC design and efficiency to deal with complex nonlinear dynamics.

In terms of processes requiring robust control,the sliver drafting process employed in textiles manufacturing represents a very good example of a continuous material processing operation with nonlinear dynamics.Here,the dynamics of the sliver drafting process play an essential role in the automatic control systems employed in textiles manufacturing for the reduction of sliver irregularities.Because a textile sliver is composed of thousands of discrete fibers,a sliver drafting system is complex,and includes inherent nonlinearity,which makes the control of such systems a challenging task.The long-term auto-leveling control of such systems is particularly challenging because instability and external disturbances are frequently observed.While a number of modern effectual control methods have been developed for auto-leveling sliver drafting systems[Kim,Lim and Huh(2012);Moghassem and Fallahpour(2011);Han,Youn-Sung,Soon-Yong et al.(2008)],and the problems associated with the modeling and control of the sliver drafting processes have been discussed in control engineering literature[Djiev(2016)],most of these methods can be applied in practical applications only when at least an approximate mathematical model of the process is available.As such,these methods lack robustness and are difficult to implement in nonlinear systems.Some studies have addressed this problem by implementing linearization methods[Guo,Chen and Hu(2003);Huang and Bai(2001)].However,attempts at linearization have not significantly contributed to the robustness of system control.In this sense,the feature of an SRWNN in the absence of a pre-existing mathematical model is uniquely advantageous.

In light of the above research focused on improving control system robustness in continuous material processing operations like the sliver drafting process,this paper proposes a hybrid feedforward-feedback nonlinear model predictive controller.Block diagram of the proposed control system is shown in Fig.1.The adaptive feedback control strategy of the controller augments the standard feedforward control to ensure improved robustness and compensation for environmental disturbances and/or parameter uncertainties.Thus,the controller can reduce the need for manual adjustments.The controller adopts a wavelet-based neural network model with high prediction precision and time-frequency localization characteristics.Online training is utilized to predict uncertain system dynamics by tuning the wavelet neural network parameters and the controller parameters adaptively.The controller applies NGPC based on a SRWNN to generate an adaptive control signal for attaining robust performance.

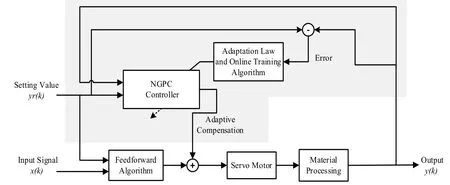
Figure 1:Block diagram of the proposed control system

This paper is organized as follows.Section 2 presents the adopted SRWNN model structure and adaptive learning algorithm.A brief description of the adaptive predictive control is introduced in Section 3,and the design procedures of the proposed control system are also described in detail.Section 4 presents the self-leveling process and dynamics of a standard sliver drafting system.The effectiveness of the proposed control system is validated by numerical simulations and experimental results involving a single-input single-output double-zone sliver drafting system.Finally,Section 5 concludes the paper.

2 SRWNN model structure and training algorithm

To obtain a prediction model for the proposed prediction control scheme that is appropriate to the characteristics of continuous material processing systems,we adopt a class of nonlinear autoregressive moving average(NARX)time-series model at time stepkas the system model:

wheref(·):R n→Ris a smooth-valued nonlinear function,kindicates the time step index,y(k)is the system output for a system inputu(k),nyandnuare the orders of the output and input,respectively,N=ny+nu,andξ(k)∈Ris a zero-mean Gaussian white noise sequence.

2.1 SRWNN model structure

The control strategy is implemented using an SRWNN model developed as an approximation of the nonlinear system given by(1).The proposed SRWNN adopted a mother wavelet layer composed of self-feedback neurons that can store the past information of the network,allowing the SRWNN to capture the dynamic response of a system.As a result,the SRWNN can be applied effectively to complex chaotic systems,even though the SRWNN employs fewer wavelet nodes than a WNN.Thus,the structure of the SRWNN can be simpler than that of a corresponding WNN,which makes the SRWNN more appropriate than WNNs for real-time control applications.

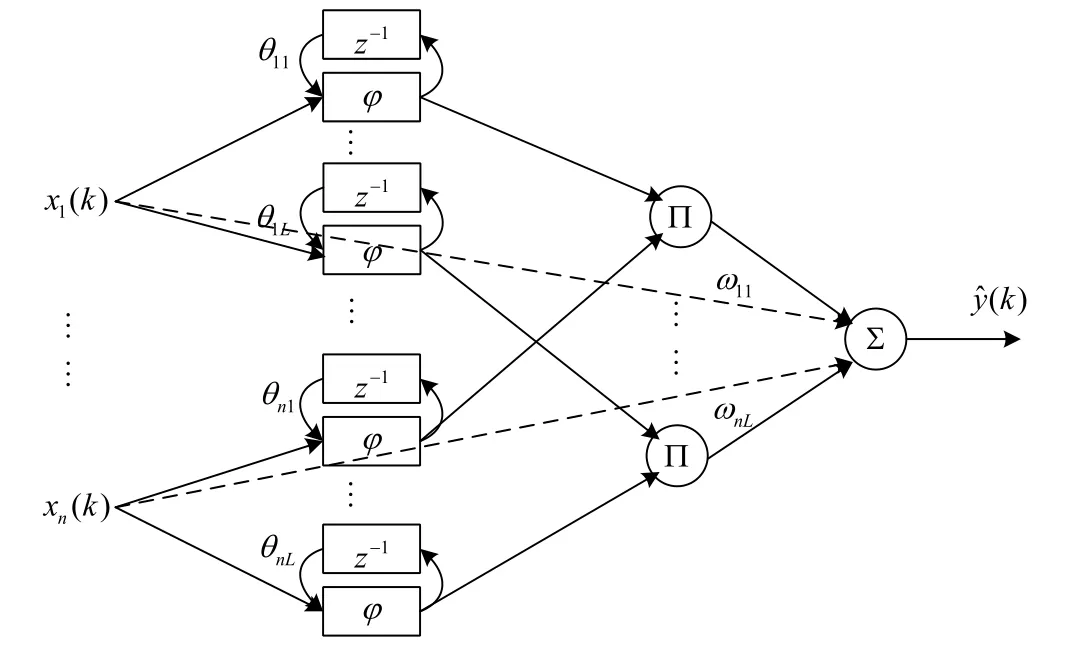
Figure 2:Schematic of the proposed SRWNN structure

A schematic illustrating a WNN and the proposed SRWNN structure is given in Fig.2.The structure comprises an input layer(layer I),a self-recurrent wavelet layer(layer II),a wavelet layer(layer III),and an output layer(layer IV)providing an estimated system outputŷ(k).Here,xi(k),i=1,…,n,is theith input of the SRWNN,θil,l=1,…,L,denotes thelth self-feedback weight of theith input directed toward a node of layer II,z-1represents delay,αiis the connection weight between the input nodes of layer I and the output nodes of layer IV,andωilis the connection weight between the product nodes of layer III and its output nodes.The signal propagation and the function expression in each layer are given as follows.

Layer I:The nodes in this layer receive the input variables and transmit them to the next layer directly.

Layer II:Each node of this layer has a wavelon and a self-feedback loop.The first derivative of a Gaussian functionis adopted as a mother wavelet.The output of this layer can be represented as

Layer III:The output of this layer is the product of all the wavelet neurons,i.e.,

Layer IV:The single-node output of this layer is a summation which combining the outputs of layer III and the adaptive input values from the input of layer I.Therefore,the output of the SRWNN is composed of all incoming signals and the assigned tuning parameters as follows:

The initial values ofωilandmilare given randomly in the range[-1,1],whiledilis given randomly in the range(0,1](i.e.,dil＞0).In addition,the initial values ofθilare given as 0,indicating an absence of feedback initially.

The aforementioned SRWNN can be used to be a universal uniform approximator for continuous functions over compact sets when satisfies specific conditions.These conditions and a detailed proof of this claim can be obtained elsewhere[Lin and Chen(2006);Lee and Teng(2000)].The leveling process discussed in our paper is a complex parametric nonlinear dynamical system,which has the random-like behavior usually shown in statistical systems although it is associated with deterministic dynamics.It can be seen as continuous function over compact sets and in the calculation process,suitable parameter constraints can make sure it satisfies the conditions.

2.2 Online training algorithm for the SRWNN

A back-propagation algorithm was adopted for SRWNN training in the purposed control system,and all weights includingmilanddilare trained via the gradient descent algorithm.The target is to minimize the following error functionJ0(k):

Applying the gradient descent method provides the following updating laws formil,dil,θilandωil.

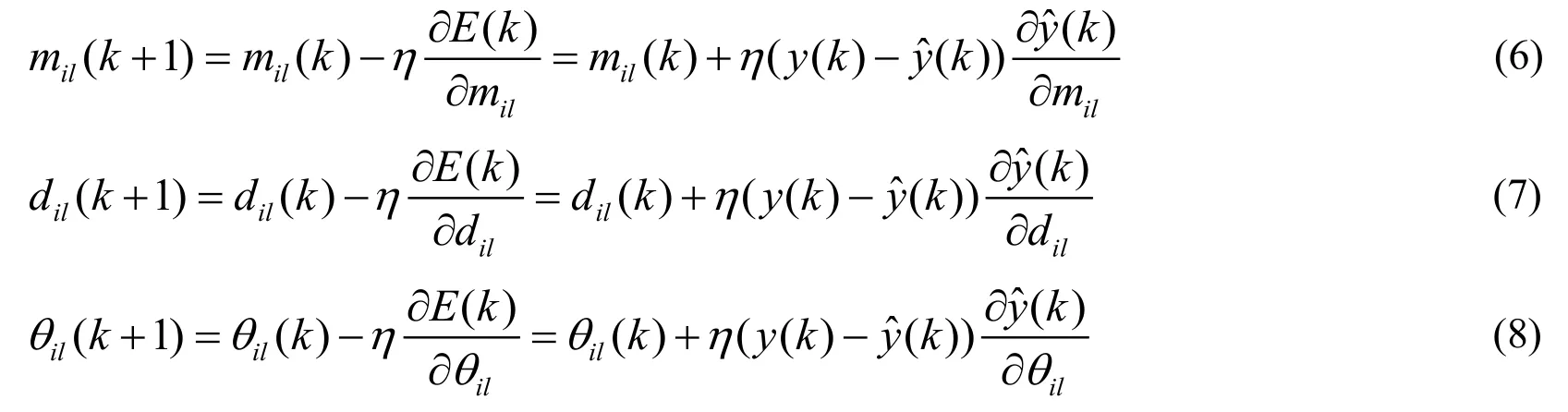
Here,ηis the learning rate,and the following definitions are applied.

3 Adaptive non-linear control strategy

The proposed control strategy was implemented here using a nonlinear SRWNN model as a predictor and the schematic of the control strategy is given in Fig.3.The task of the predictor is to predict plant output based on the regressed inputs at each sampling time.This is conducted for all control operations within an established prediction range.The value of the control horizon should always be less than the value of the prediction horizon.A diophantine equation is used to solve and minimize the complex real-time optimization cost function at each sampling time to determine the optimum control inputs that yield the least error between the predicted output and the trajectory reference signals and which minimize the controller efforts[Astrom and Wittenmark(1994)].

Figure 3:Structure of the predictive control strategy

To derive the NGPC law and to find the j step-ahead prediction of y(k),the SRWNN model(4)is rewritten as

whereΔ=1-z-1is the difference operator,

The system parametersailandbil,that isωil,inA(z -1)andB(z -1)are estimated online with variable forgetting factor recursive least square method(VFFRLS)adaptively.From Eq.(12),

The parameters are obtained by the following formula:

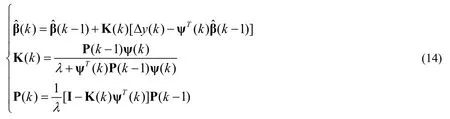
λ(0 ＜λ＜1)is the forgetting factor.

In order to get the optimal predictions,Eq.(12)could be simplified as

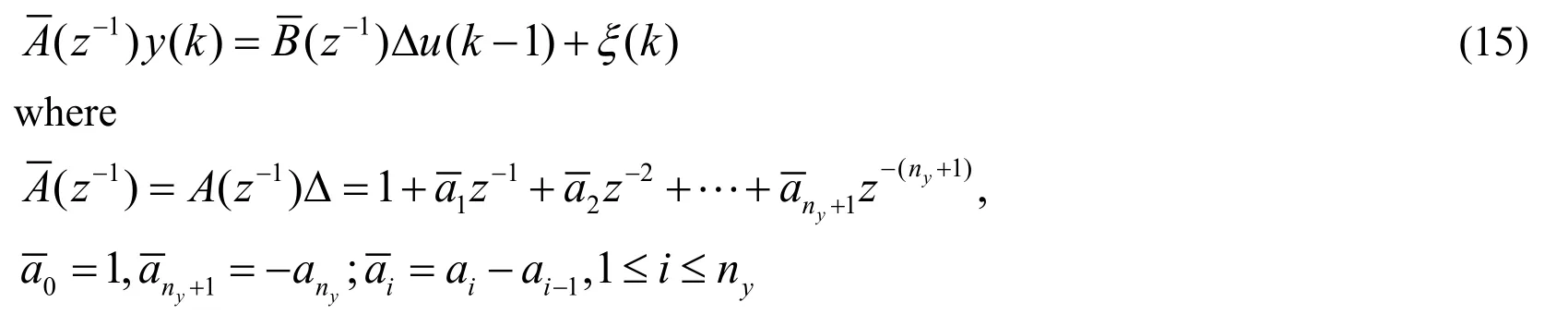
The proposed control law is derived to minimize the expected valueE[·]of the following predictive performance criterion:

Here,npis the prediction output horizon,andyr(k+j)is a known bounded reference output for the discrete timek+j.In general,npis chosen to encompass all the responses that are significantly affected by the present control.Here,np Tsis typically the same magnitude as the rise time of the controlled system based on the sampling timeTs[Astrom and Wittenmark(1994)].

In order to optimize the cost functionJ(k),the predictiony(k+j)forj ≥ 1andj ≤ Npwill be obtained.Consider the following Diophantine equation:

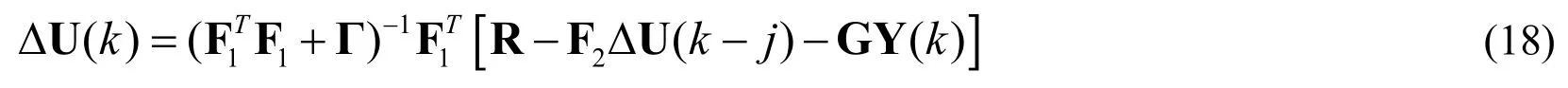
where the following definitions are applied.

The resulting overall system has been proven to be stable[Lu(2009)].Assuming that the parametersmil,dil,θilandωilin(4)are updated according to(6)-(8)and(14),the proposed SRWNN algorithm is convergent,provided thatηsatisfies the following condition:

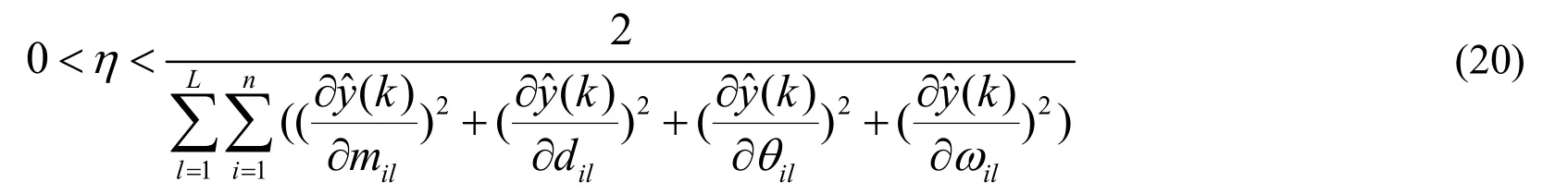
This convergent condition of the purposed process are verified for a chosen Lyapunov function,and the detailed proof can be obtained elsewhere[Yoo,Park and Choi(2005)].To guarantee thatηresides within this stable region,we apply an adaptive learning rate for the SRWNN as follows:

From the above,the implementation of the adaptive control procedure can be summarized as follows,and the state flow chart of the calculation process is shown in Fig.4

(2)Measure plant outputy(k)and the reference tracking outputyr(k+j);

(4)Solve the Diophantine Eq.(17)and obtain;

(5)Construct the vector R,Y(k),Δ U(k-j)and matrix F1,F2,G;

(6)Calculate and implementu(k)via(19);

(7)Repeat Steps 2-6.

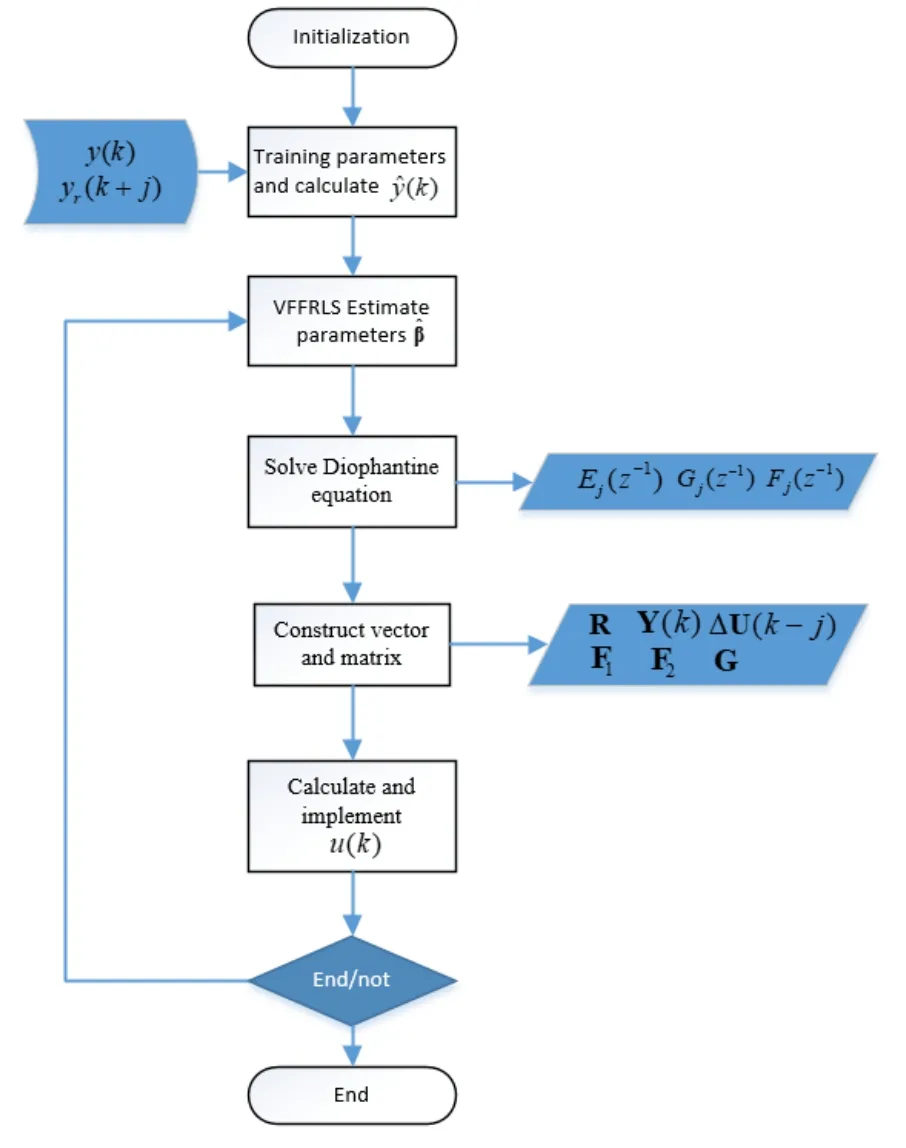
Figure 4:State flow chart of the calculation process

4 Numerical simulations and experimental results

4.1 Sliver drafting process dynamics and auto-leveling control

A frequently-used auto-leveling system for a double-zone sliver drafter is illustrated in Fig.5.The positions of the fibers with respect to each other and the numbers of fibers within cross-sections are affected by the different speeds of the rollers[Hlava(2003)].At each sampling timek,displacement sensors 1 and 2 obtain the thickness of the input sliverx(k)and the thickness of the output slivery(k),respectively,from which the linear densities of the respective slivers are calculated.In this system,variations in the input sliver linear density can be seen as the dominating disturbance,which greatly affects the uniformity of the output sliver.Usually,this variation is stochastic with occasional step-like disturbances owing to nubs in the input sliver,or when changes in the characteristics of the input sliver(e.g.,batch of material)affect.In addition to this measured disturbance,a number of other unmeasured disturbancesv(k)(e.g.,environment moisture change,stacking of cotton fiber)can affect the quality of the output sliver,and these can also be treated as stochastic disturbances.

A conventional auto-leveling feedforward control algorithm is a simple linear adjustment based on reference valueyr(k)and the measurementsx(k)from sensor1.In existing feedforward strategies,x(k)serves as an independent input that directly affectsy(k)according to a pre-established parametric model used to describe the drawing process.Accordingly,the irregularity of the output sliver is managed by sending the signal from sensor 1 to the controller to determine the control signal,which then adjusts the velocities of the drawing rollers using the servomotor to obtain an appropriate drawing rate.The signal from sensor 2 strictly serves a monitoring purpose,without participating in the automatic control process.This process allows the controller to compensate immediately for the impact of variations inx(k)ony(k)rather than waiting until the effect appears in the output.Thus,feedforward control ensures the short-term uniformity of the output sliver.In addition,the parameters of the parametric model employed in feedforward control are subject to change if the input sliver material or its characteristics are altered.

Figure 5:Schematic of a standard feedforward controlled auto-leveling sliver drafting system

The proposed compensation controller consists of a conventional auto-leveling control strategy in the feedforward component in addition to an online trained NGPC controller in the feedback loop.In this control method,the signal of Sensor 2 is used in the controller to automatically compensate for performance degradation.While the feedforward controller compensates immediately for the measured disturbance,the proposed SRWNN-based model predictive controller provides feedback compensation for unmeasured disturbancesv(k).Here,unmeasured disturbances represent an independent input that is not affected by the controller or the plant,and is always potentially present,but is only observable fromy(k).Unmeasured disturbances represent unknown,unpredictable events that are best addressed as un-modeled system dynamics.Therefore,all information based on the outputy(k)obtained from Sensor 2 is fed back to the NGPC controller.Then,the proposed NGPC controller observes the future behavior of the sliver drafting system and compares the actual performance to a desired reference model performance,and accordingly calculates the control input that will optimize plant performance over a specified future time horizon.The learning algorithm modifies the parameters of the NGPC controller online based on the model-following error(MFE)to obtain a match with the desired reference model response.

4.2 Numerical simulation of the auto-leveling control system

Simulation results are presented to verify the feasibility of the proposed SRWNN-based NGPC control scheme under various operating conditions.All algorithms were developed using MATLAB/SIMULINK in a control computer.In the simulations,the disturbance rejection capabilities of the auto-leveling system were evaluated under different long-term low-frequency disturbancesv(k)effecting on the plant.

Simulation 1:

At first,the two sensors data of feedforward control,x(k)andy0(k)(voltage),collected in advance are used for offline simulation.A nonlinear model for the sliver drafting process was identified by an identification experiment with a sampling period of 0.001 second,and this model serves as the plant model in our simulation[Chun,Bae,Kim et al.(2006)].Referring to the system model(1),the input variables of the SRWNN model are specified by{y(k-1),y(k-2),y(k-3),u(k-1),u(k-2)}.After removing mean,training the network parameters of the SRWNN using the input-output data,selecting the key parameter of the SRWNN asL=3 was found to be effective for this nonlinear system.The prediction horizon of the proposed control law was selected asNp=9.Then the proposed controller was employed to match the system outputy(k)to a reference output yr(k),where yr(k)=0 and the external disturbancev(k)was specified as follows:

Case 1:v(k)=0.07sign(sin(4πkts)),

Case 2:v(k)=0.07sin(4πkts),

where sign(·)represents the signum function andtsis the sample time.These two cases represent long term perturbation under a step disturbance and a sinusoidal disturbance,respectively.The results for case 1 and case 2 are shown in Figs.6(a)and 6(b),respectively.The individual plots show the input thickness signalsx(k),and the output thickness signalsy(k),control errorse(k),and the control signalsu(k)of the conventional feedforward auto-leveling controller(denoted by the subscript 0)and the proposed controller.

These figures clearly indicate that good dynamic performances,in terms of command tracking and drift restraint,are realized for the auto-leveling system.From the change of input and output sensor datax(k)andy(k),the evenness of the sliver has improved after auto-leveling,in addition,the error with the average sliver thicknessey(k)is smaller thaney0(k),which means that the control effect is enhanced by the proposed method comparing with the traditional approach.Seen fromu(k),the algorithm is convergence with step disturbance(a;case 1)and sinusoidal disturbance(b;case 2).

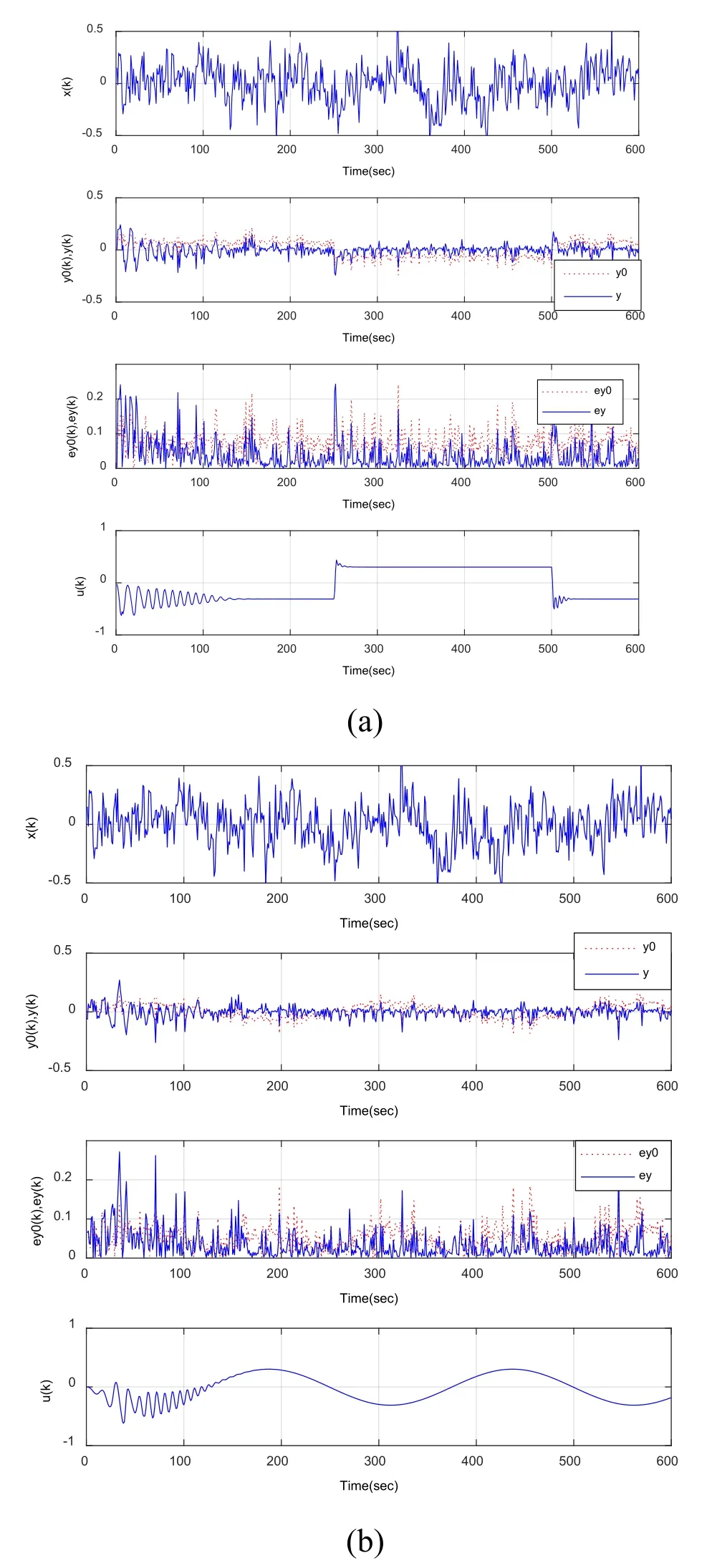
Figure 6:The input thickness signals x(k),and the responses of the conventional feedforward auto-leveling controller(denoted by the subscript 0)and the proposed controller for a reference output yr(k)=0 with a step disturbance(a;case 1)and a sinusoidal disturbance(b;case 2)

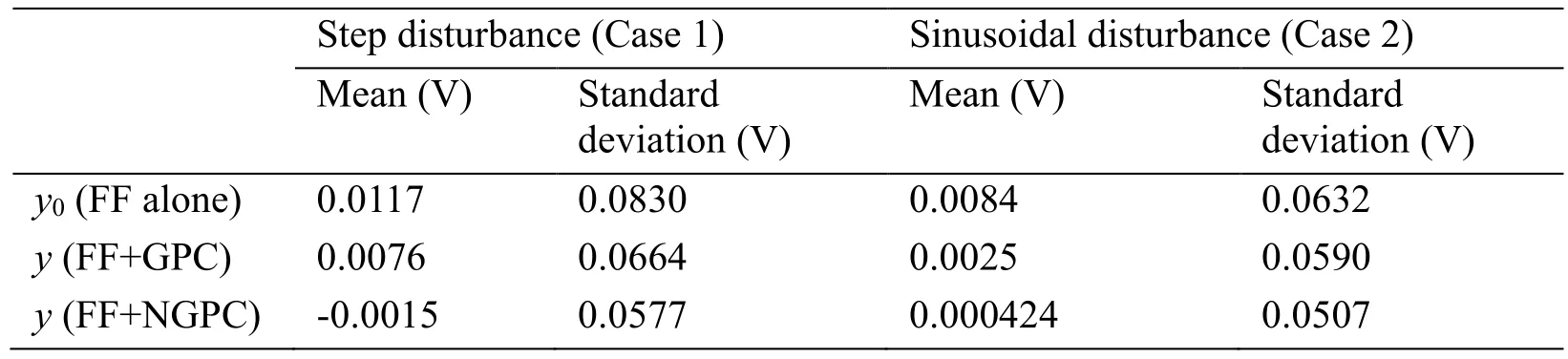
Table 1:Simulation results of feedforward control(FF)alone,FF in conjunction with a standard GPC controller(FF+GPC),and the proposed control system(FF+NGPC)in terms of the controlled output y(k)relative to a reference output yr(k)=0

Simulation 2:

In order to verify the validity of the algorithm for long segment evenness,20000 sampling of output sliver thickness withTs=0.01 s are analyzed.The simulation results are listed in Tab.1 in terms of the mean and standard deviations ofy0(k)andy(k).We note from the table that,compared with the results obtained using the standard feedforward control,the mean values ofy(k)obtained using the proposed controller were decreased by 87.18% and 94.95% for Cases 1 and 2,respectively,and the corresponding standard deviations ofy(k)were decreased by 30.48% and 19.78%,respectively.Accordingly,we can conclude that the proposed controller can greatly reduce the nonuniformity of the output sliver relative to that obtained using only feedforward control.Tab.I also includes the mean and standard deviations ofy(k)obtained using feedforward control in conjunction with a conventional GPC controller[Clarke,Mohtadi and Tuffs(1987)].As seen from the results,the performance of the proposed controller is significantly better than that get from the conventional GPC controller.

Simulation 3:

To test the robustness of the proposed auto-leveling controller,we conducted a simulation in which the system parametersailandbilwere varied by ±5% after plant operation for 300 s.The results are shown in Fig.7,which illustrate that the proposed SRWNN-based NGPC controller can adapt to arbitrary changes of the plant parameters.The control error reveals no significant increase after the parameter changed.

The simulation results indicate that the SRWNN-based NGPC controller demonstrates satisfactory tracking performance and system robustness.

Figure 7:Output tracking and error responses in case of system parameter variations operative after 300 s

4.3 Experiments on a double-zone sliver drafting system

The experimental results were obtained using an STM32 microcontroller integrated circuit(STM Electronics)and a field programmable gate array(FPGA)control board.The input,self-recurrent wavelet,wavelet,and output layers of the SRWNN included 2,14,7,and 1 neurons,respectively.The output response in terms ofy(k)with the proposed SRWNN-based NGPC controller is shown in Fig.8.Here,the values were estimated from 20,000 consecutively sampledy(k)data with hardware sampling frequency 1000Hz.Tab.II lists the mean thickness and coefficient of variation(CV)of the output slivers respectively obtained using feedforward control alone and using the proposed controller to regulate the speed of the back roller.The values here are recorded by a USTER evenness tester,which is a professional sliver testing equipment in textile factories and laboratories.Obviously,the control method proposed in this paper can regulate the mean thickness at the desired value,and the CV of the sliver can be substantially reduced.

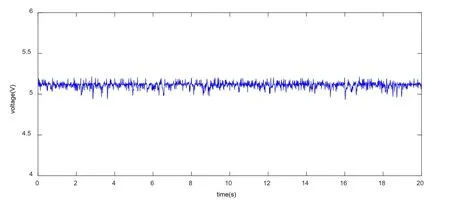
Figure 8:The measures value of displacement Sensor 2(y(k))obtained over time using the proposed SRWNN-based NGPC controller

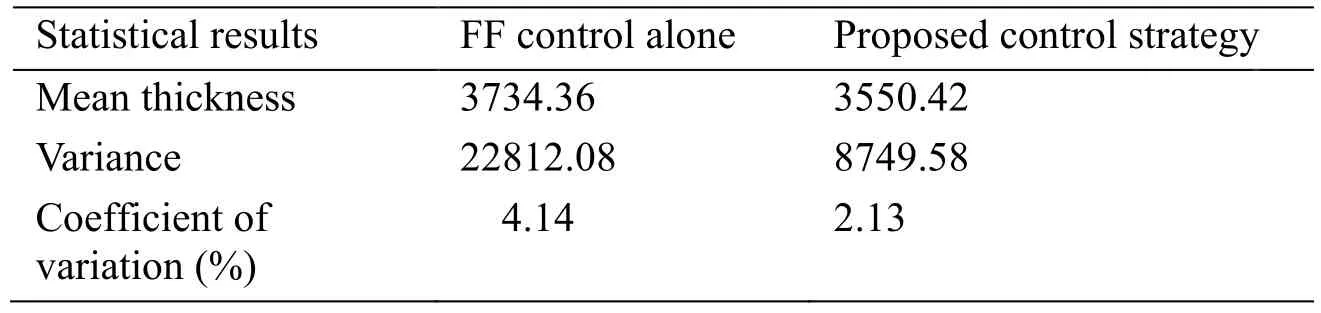
Table 2:Output sliver thickness values obtained during experimental testing

5 Conclusion

This paper proposed an online-trained adaptive SRWNN-based model prediction controller for continuous material processing systems.The SRWNN was employed for establishing a discrete-time model for the nonlinear system dynamic,and the NGPC controller functioned as adaptive feedback compensation for augmenting the existing open-loop feedforward control,and for providing improved setting value tracking and external disturbance resisting capabilities.The proposed NGPC algorithm,including the adaptive learning rate for the training of SRWNN model weights,was applied to a sliver drafting process,and the simulation results indicates the better stable tracking ability and adaptability,comparing with the traditional control strategy.The physical experiments verified that the proposed control system is effective for ensuring the long-term uniformity of slivers both with and without input sliver irregularities and external noise disturbances.