江坪河面板堆石坝二期面板浇筑方案研究

2019-11-07王国辉关少恒

水电与新能源 2019年10期

王国辉，岳强，关少恒，陈兴，周伟

(1.中国电建集团中南勘测设计研究院，湖南长沙 410014；2.武汉大学，湖北武汉 430072)

混凝土面板堆石坝具有经济、取材方便、结构简单、对气候和地基适应性强、抗震性能好、安全性高、维护方便等特点，因而成为极具竞争力的坝型，自20世纪70年代兴起以来，已得到长足发展，工程规模和施工技术在逐渐成熟，国内外水利水电工程建设中被广泛采用[1-3]。随着高面板堆石坝经验技术的不断积累，我国高面板堆石坝已迈入200 m级建设阶段，其中，水布垭面板堆石坝最大坝高233 m，为世界最高已建面板堆石坝；江坪河面板堆石坝最大坝高219 m，为世界在建最高面板堆石坝；此外，古水、马吉、茨哈峡等一批更高的工程也在规划或可研中[4]。

而随着坝高的不断增长，面板堆石坝的应力变形控制逐渐成为维护大坝安全的核心内容，混凝土面板作为大坝的主要防渗结构，其安全可靠程度更是工程关注重点[5]，部分已建200 m级高坝在建设运行过程中出现了面板挤压破坏、面板裂缝、大范围脱空及大量渗漏等问题，这些工程经验都给新建高面板堆石坝提供了警醒与借鉴。因此，在面板浇筑前对其进行合理的设计及对应力变形进行预测显得尤为重要。本文利用有限元分析软件，采用面板子模型法[6]，对江坪河混凝土面板堆石坝的坝体及面板的应力变形进行了分析，为江坪河工程二期面板的合理浇筑提供了理论依据。

1 工程概况

江坪河水电站位于溇水干流上游河段，湖北省鹤峰县走马镇阳河乡。溇水是澧水的最大支流，地跨湘、鄂两省，发源于湖北省鹤峰县下坪镇七垭村，流向自西北向东南，于湖南省慈利县城汇入澧水。溇水全长250 km，流域面积5 048 km2。江坪河坝址以上河段长113 km，流域面积2 140 km2。坝址多年平均流量为81.10 m3/s，多年平均径流量为25.6亿m3。正常蓄水位470.00 m，水库总库容为13.66亿m3，电站总装机容量为450 MW。坝顶高程为476.0 m，坝顶宽10.0 m，坝顶长度414.0 m，最大坝高219.00 m。大坝上游坡比为1∶1.4，下游综合坡比为1∶1.4，局部坡比1∶1.36。

坝址位于峡谷河段内，峡谷河道长约600 m，河谷断面呈V型，坝轴线处河谷宽高比约1.8，属狭窄河谷，坝址区为岩溶峡谷，两岸山体雄厚，左右岸均有不对称冲沟发育。大坝一、二期混凝土面板厚度沿高程变化，按式t(板厚)=0.3 m+0.003 6H(H为计算断面至高程472.00 m的高度)确定，三期为等厚面板，厚度：t=0.559 m。三期面板混凝土强度等级采用C30，一、二期面板混凝土强度等级采用C35，抗渗等级W12，抗冻等级F100。

2 计算模型及参数

2.1 有限元计算模型

江坪河面板堆石坝共离散为43 643个单元，62 942个节点，主要采用8结点6面体单元，为适应边界过渡，采用部分棱柱体单元，江坪河面板堆石坝三维有限元计算模型及坝体材料分区示意如图1(a，b)所示。三维计算模型中，坝体部分单元大小为8 m左右，并针对特殊部位及重点研究部位进行精细建模；面板部分单元长边为3 m左右，沿厚度方向分为三层建模。图中X轴正方向为顺河向指向下游，Z轴正方向为横河向指向右岸。

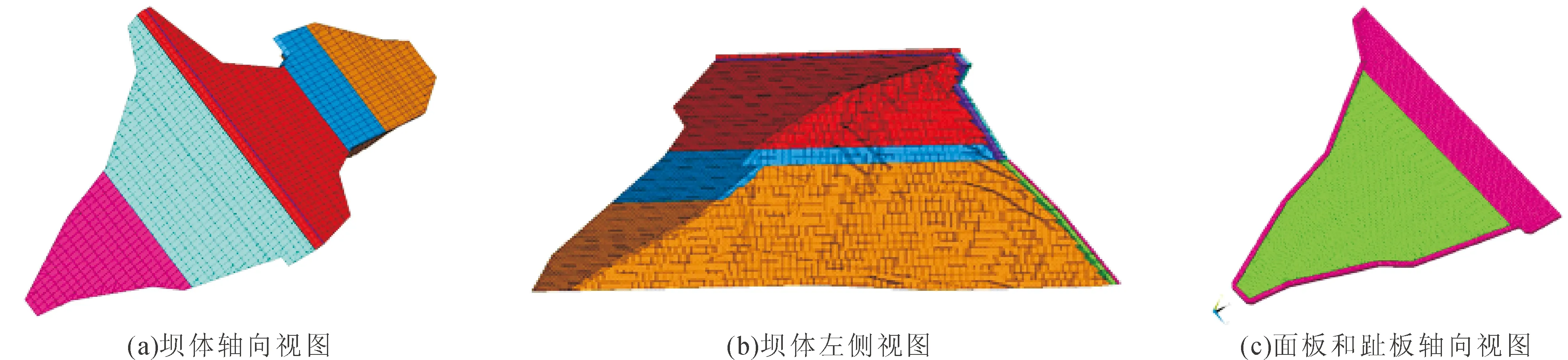
图1 大坝三维有限元计算模型图

2.2 面板子模型法

考虑高面板堆石坝实际的施工特点和面板分期浇筑特点，提出采用子模型法分析面板的应力变形，而面板与挤压边墙之间的特殊边界采用基于莫尔-库仑准则的无厚度接触摩擦单元进行模拟。本文对接触模型的研究采用基于扩展Lagrange乘子法的摩擦接触单元，已经有研究表明[6-8]，这种方法能够更加真实有效的模拟面板接缝变形。接触问题求解方法一般是利用变分原理用有限元进行离散，然后构造合适的迭代格式进行迭代或者数学规划方法求解。由弹塑性接触分析的最小势能原理，在所有满足求解区域内的应力应变关系和位移边界条件可能增量位移场中，真实解应使弹塑性系统总势能取最小值。

=(ε，u，λ)=

(1)

C(u)=un-g0

(2)

式中，g0为接触面初始间隙。

基于Lagrange乘子法求解接触摩擦问题时，对3种接触状态即分离、黏合、滑动分别按以下准则进行接触状态的判断：

1)分离状态。当接触面之间法向应力大于0时，接触面张开。

2)黏合状态。当法向应力σn小于0时，且接触面切向剪应力小于摩尔库伦准则所规定的允许剪应力，接触面处于黏合状态，接触面的切向剪应力公式如下。

τ=ksδu≤f|σn|

(3)

式中：δu为接触面的相对位移；ks为剪切模量；f为库伦摩擦因数。

3)滑移状态。当法向应力为压应力时，且根据摩尔库伦摩擦公式计算接触面切向剪应力大于摩尔库伦准则允许剪应力，接触面处于滑动状态。

接触面张开是所不能承担的应力和接触面发生滑移时超过抗剪强度的那部分将通过扩展Lagrange乘子经过增量迭代转移并重新分配给周围单元。

上述接触面状态判断表述为以下扩展Lagrange乘子法的接触约束条件：

σn=<λ+ηc(u)>

(4)

Φ=|τ|-fσn≤0

(5)

(6)

ξ≥0

(7)

ξΦ=0

(8)

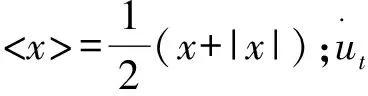
有限元计算中采用8节点单元对接触进行模拟，该单元根据下覆实体单元或壳单元可以退化为6节点单元，单元详细示意图如2所示。

图2 接触单元模型图

图2中，Associated Target Surfaces表示目标接触面；Contact Elements表示接触单元；Surface of Solid/Shell Element表示实体或者壳单元表面。单元局部坐标系中，R表示各向同性摩擦单元X轴，X0表示正交各向异性摩擦且未使用单元局部坐标系时单元的X轴，X表示正交各向异性摩擦使用单元局部坐标系时的单元X轴。

3 顶部高程敏感性分析

大坝已确定一期面板顶部高程360 m，三期面板顶部高程472 m，计算拟定二期面板浇筑时间为5月1日至6月30日，分别选取二期面板顶部高程为420、425、430、435，计算面板稳定期应力变形，结果显示，各方案下的面板整体分布规律一致，当二期面板顶部高程采用430 m时，稳定期的面板应力变形水平见图3～图6。位移方面：轴向位移指向河床中部，河床中部为面板轴向位移的中性面，轴向位移大致以中性面对称，且最大轴向位移发生位置靠近面板中部，在面板板块之间，坝轴向位移出现不连续现象；面板挠度垂直指向坝内，最大值出现在一期面板上部。应力方面：面板轴向中部受压，两侧受拉，压应力最大值出现在一期面板中部，拉应力均发生在面板两侧边缘；顺坡向中部受压，在面板上下部及边缘部位受拉，压应力最大值出现在二期面板中部，在面板拐角处易产生应力集中。

图3 稳定期面板挠度图

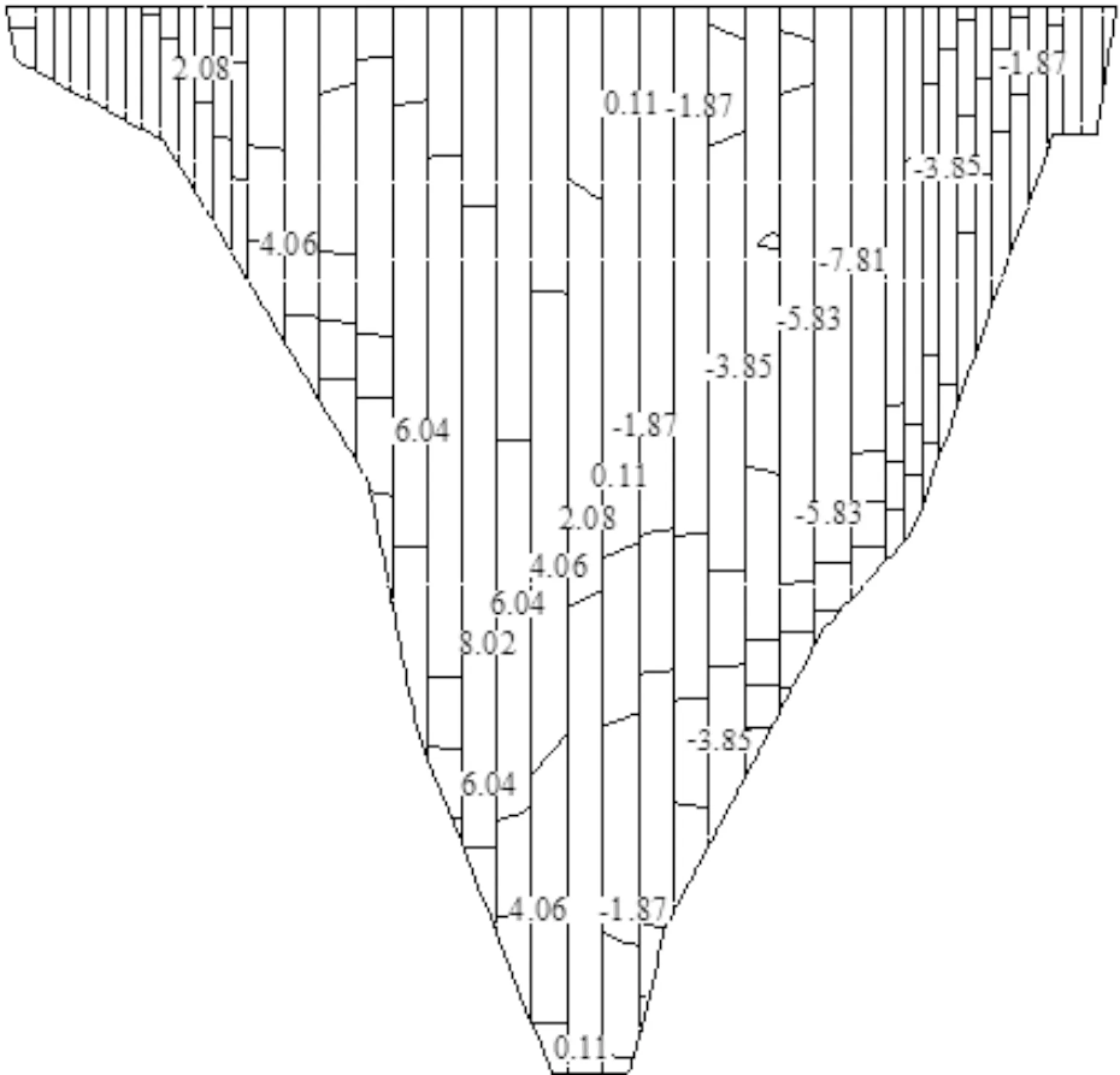
图4 稳定期面板轴线位移图

图5 稳定期面板顺坡向应力图

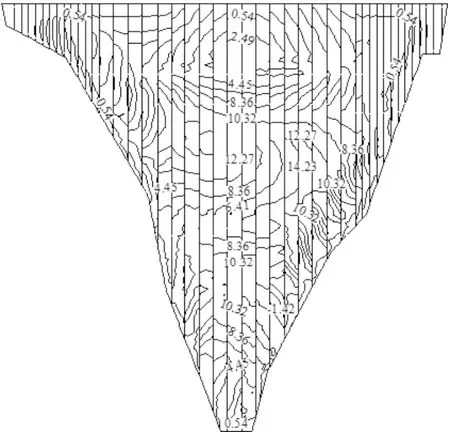
图6 稳定期面板轴向应力图

不同二期面板顶部高程方案的稳定期面板应力变形极值见表1，超过一定压力值的受压面板区域所占面板总面积的百分比见表2。由表可知，四种高程方案稳定期的面板变形差别很小，面板向左岸的轴向位移为7.5 cm左右，向右岸轴向位移为8 cm左右，面板挠度在40 cm左右；在面板应力方面，轴向4个高程方案的轴向压应力基本相同，拉应力方面，高程420 m和425 m的拉应力相对较小；顺坡向压应力方面高程420 m和425 m的压应力相对更小，拉应力最大值基本相同。通过超过一定应力值的受压面板区域占面板总面积百分比可知轴向应力约73%的面板区域受压，顺坡向应力约95%的面板区域受压，大于指定压力值的区域面积随着面板顶部高程的提高有逐渐增大的趋势。

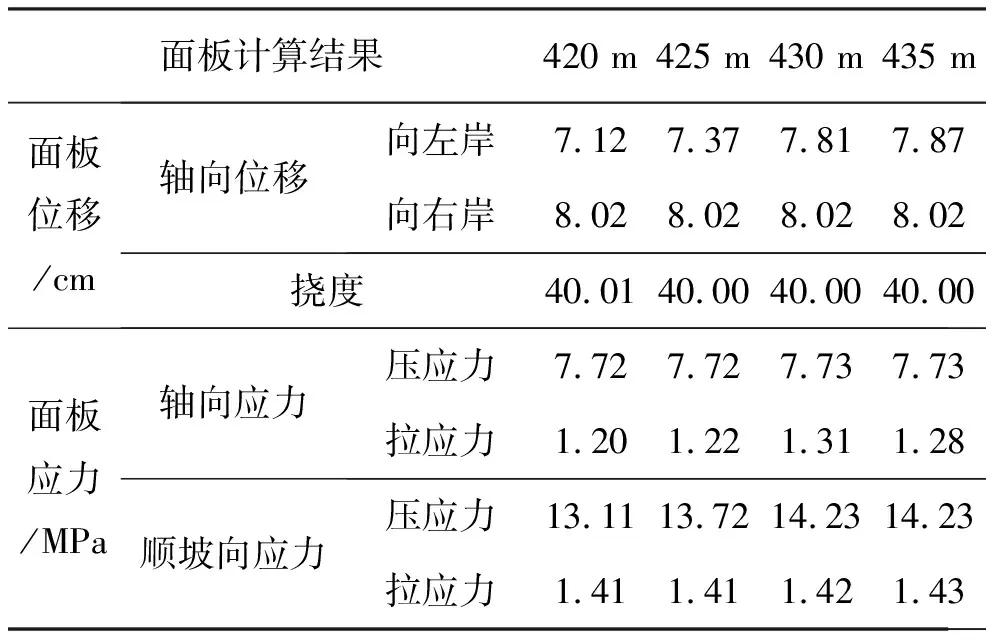
表1 不同顶部高程的二期面板稳定期计算结果表

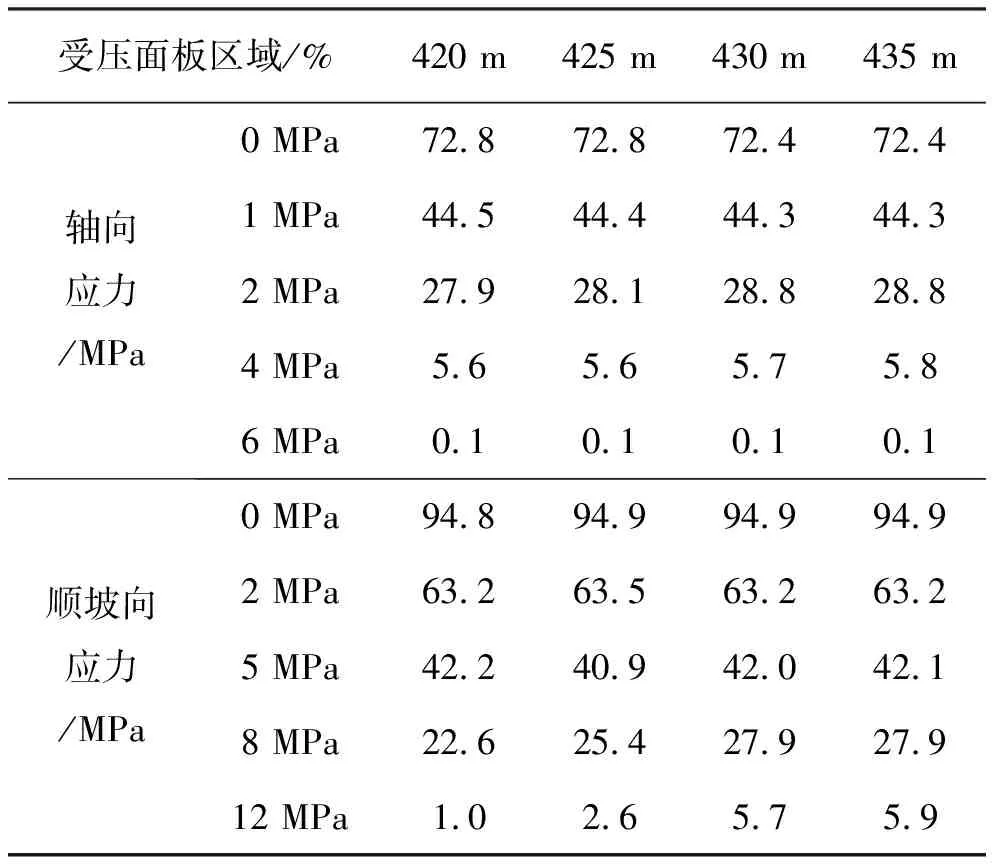
表2 超过一定压力值的受压面板区域表

由以上分析结果可以看出，在一定范围内，随着二期面板顶部高程的升高，江坪河面板堆石坝的面板在稳定期的应力位移分布规律基本一致，其位移几乎没有变化，而应力水平有逐渐增大的趋势，同时受压面积不断增大，从这方面来讲，面板顶部高程增加有助于减小拉应力的数值及面积，防止产生拉性裂缝，但不利于对最大压应力的控制。

4 浇筑时机敏感性分析

同时面板浇筑时机也对面板的安全运行存在着巨大影响，为了探究二期面板的适宜浇筑时间，在大坝最大典型断面的上游坝坡垫层区表面二期面板高程附近选取一排特征点，提取二期面板浇筑时期特征点的沉降速率和脱空值，并计算最大脱空长度，特征点位置示意图见图7。

图7 最大断面垫层区表面特征点分布图

分别假定二期面板开始浇筑时间为5月1日、6月1日、7月1日、8月1日、9月1日，对上游坝坡变形进行计算并提取特征点沉降数值，特征点高程及沉降速率计算结果如表3所示，其中沉降速率以向下为正。

表3 不同时间点上游坝坡特征点沉降速率表mm/月

由表3可知，上游坝坡面的堆石体沉降速率随坝体高程的升高而增大，这与坝体最大断面的沉降速率随高程变化的规律一致；从高程390 m到高程430 m的面板法向变形速率都为正值，375 m高程以下的坝坡沉降速率基本稳定在0.9 mm/月附近。这是因为坝体上部以变形仍以沉降为主，375 m高程以下的坝体经过停工期后流变基本收敛，变形基本趋于稳定；不同浇筑时机下高程375～430 m坝坡的沉降速率最大值为4.0～4.7 mm/月，速率波动主要与上部坝体的平均填筑强度有关。基本都在允许接受范围之内。

同时，面板脱空量也是影响面板浇筑时机的重要因素，本文计算了各工况下三期面板浇筑前二期面板的脱空量，脱空判断的下限值为1 cm，即脱空位移大于1 cm时，认为面板产生了脱空。不同浇筑时机的二期面板脱空位移及最大脱空长度见表4。