连云港市1956—2018年降水变化特征研究

(江苏省水文水资源勘测局连云港分局，江苏 连云港 222004)

降水是水文循环的基本环节，也是地表径流的本源和地下水的主要补给来源，对水资源的丰歉程度影响很大；降水在空间上分布不均匀与时间上不稳定又是引起洪涝旱灾的直接原因，进而影响着人民的生产和生活。在全球气候变暖和快速城镇化的条件下，开展降水量的变化特征及规律研究，对水资源管理与防汛抗旱具有重要意义。本文采用一致性、可靠性、代表性较好的具有1956—2018年完整系列的33个降水量站的观测数据，对连云港降水的相关特征及规律进行系统分析，为地方水资源开发利用管理以及防汛抗旱提供决策依据，为其他水文序列特征分析提供可以参考的研究方法。

1 研究区域概况

连云港市地处淮河流域沂沭泗水系下游，东临黄海，属暖温带湿润性季风气候，四季分明，多年平均年降水量为894.5mm，大致自南向北、自东南向西北方向递减。降水量等值线的范围在860～940mm之间，灌云县南部和灌南县中部为全市降水量最大地区，最小降水量集中在赣榆区北部、东海县西部以及灌南县东部。降水年际变化较大，年最大降水量为1308.0mm，年最小降水量为588.0mm，两者相差720.0mm，极值比为2.2，变差系数为0.20。连云港降水年内分配不均，汛期(5—9月)的降水总量占全年的76.7%，其中6—8月的降水总量占全年的58.9%，1—3月和10—12月降水基本相当。降水以7月为中心呈正态分布，7月的降水量占全年的26.9%，接近全年的1/3，是各月占比最大的月份。

2 丰平枯划分

将距平百分率K作为划分降水丰、平、枯的依据，计算公式如下：

(1)

式中K——距平值，%；

Pi——第i年的降水量，mm；

将K小于-20%的年份划分为枯水的年份，将K介于-20%～-10%的年份划分为偏枯的年份，将K介于-10%～10%的年份划分为平水年份，将K介于10%～20%的年份划分为偏丰年份，将K大于20%的年份划分为丰水年份(见表1)。

表1 连云港市降水丰平枯年划分标准及成果

3 变化趋势分析

一元线性趋势检验回归模型常用于降水量序列的变化趋势分析，回归系数的显著性检验常用t检验法。一元线性趋势检验回归模型为

y=b0-b1x

(2)

(3)

(4)

(5)

(6)

式中y——降水量序列；

x——时间序列；

b0——截距；

b1——线性方程的斜率，即时间序列的平均趋势变化率。

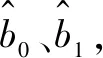
(7)

回归系数的显著性检验采用t检验法，即检验因变量y对自变量x的影响程度是否显著。

检验的原假设：H0：b1=0；对立假设：H1：b1≠0。

(8)

(9)

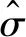
4 多时间尺度特征分析

4.1 小波函数

小波函数指的是具有振荡特性，在有限的区域内可以迅速衰减到0的一类函数φ(t)：

(10)

φ(t)为小波基函数，可以通过伸缩和平移而得到一族函数：

(11)

式中φ(t)——连续小波(或分析小波)；

a——尺度因子，相对应的1/a为频率ω；

b——时间因子。

在水文时间序列中常采用复值Morlet小波函数：

φ(t)=eiωte-t2/2ω

(12)

式中要求ω≥5的常数，取ω=6，i为虚数。复值小波变换更适合进行水文时间序列周期分析。

4.2 小波变换

若t对于时间序列f(t)∈L2(R)，其连续小波变换函数为

(13)

其中，Wf(a,b)为小波变换系数。但是在现实中，水文时间序列经常是离散型的，如f(kΔt)(k=1, 2,…,N；Δt为时间间隔)，则式(13)的离散形式为

(14)

Wf(a,b)能同时反映时域参数b和频域参数a的性质。如果a减小，那么对频域的分辨率就会变低，对时域的分辨率就会变高；否则，相反。因此，小波变换能够实现窗口的大小不变化、形状可变化的时频局部化的效果。

Wf(a,b)随频域a和时域b变化，能够绘制以时域b、频域a为横纵坐标的Wf(a,b)的二维等值线图，即小波变换系数等值线图。当时间尺度a不变时，小波变换系数为正时表示偏多期，即丰水期，小波变换系数为负时表示偏少期，即枯水期；小波变换系数的绝对值越大，表示此时间尺度变化越明显。通过以上研究，可以分析水文序列多时间尺度演变。

将所有与时间尺度a有关的小波系数进行积分，就可以得到其小波方差，其公式为

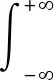
(15)

在尺度一定下，小波方差Var(a)数值则表示该时间尺度周期波动的能量大小。小波方差随时间尺度a变化的过程即为小波方差图。小波方差图能够反映出水文时间序列中所包含的不同周期波动及它们的能量大小。因此，通过小波方差图可以简单直观地确定出一个水文时间序列中存在多少个周期，有几个起主导作用的主要周期。

Morlet小波伸缩尺度a与周期T有如下关系：

(16)

式中，c为常数，取6.2。

5 特征分析

5.1 丰平枯特征

对连云港1956—2018年降水进行距平百分率计算，得到相应降水量值(见表2)，进而划分1956—2018年的丰平枯年份，枯水及偏枯年份共计23年，占比36.5%；平水年份共计19年，占比30.2%；丰水及偏丰年份共计21年，占比33.3%。根据对1956—2018年连云港降水长系列的分析，枯水及偏枯年份、平水年份、丰水及偏丰年份基本相当，枯水及偏枯年份略多，因此，连云港降水量基本稳定。

表2 连云港市降水丰平枯年划分标准及成果

5.2 变化趋势

根据连云港1956—2018年降水资料，绘制年降水过程线(见图1)，根据一元线性趋势回归模型分析，得到经验回归方程y=3830.5-1.4776x，斜率为负，表示趋势变化率小于0，说明连云港市降水序列具有减小的趋势。

图1 连云港市1956—2018年降水过程线

5.3 多时间尺度特征

将1956—2018年降水过程f(nΔt)(n=1,2,…,63;Δt=1)和Morlet小波函数代入式(14)计算，取不同的a和b，得到小波变换的模平方和实部，绘制成图(见图2、图3)。

图2 连云港年降水量小波变换的模平方时频分布

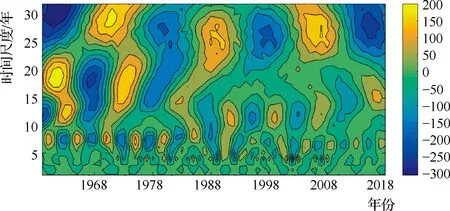
图3 连云港年降水量小波变换的实部时频分布

图2给出了不同时段各时间尺度的强弱分布，25～32年时间尺度变化很强，有两个振荡中心，最强的发生在1959—1976年，振荡中心在1959年；另一个发生在2002—2018年，振荡中心在2018年。17～21年时间尺度变化较强，主要发生在1959—1978年，振荡中心也在1959年。3～5年和6～9年时间尺度变化比较弱。

从图3可以清晰地看出连云港市年降水量时间尺度变化、相位结构，25～31年时间尺度最明显，丰枯交替出现，中心时间尺度为28年左右。

图4给出了连云港市年降水量时间序列的小波方差图。从图中可以看到，年降水量序列具有4年、7年、19年和28年左右的周期，其中第一主周期为28年、第二主周期为19年。

图4 连云港年降水过程小波方差

6 结 论

全市降水量时空分布不均，空间上大致自南向北、自东南向西北方向递减。降水量等值线的范围在860～940mm之间。时间上年际变化较大，年最大降水量为1308.0mm，年最小降水量为588.0mm，两者相差720.0mm，极值比为2.2，变差系数为0.20；年内分配不均，汛期(5—9月)的降水总量占全年的76.7%。

枯水及偏枯年份共计23年，占比36.5%；平水年份共计19年，占比30.2%；丰水及偏丰年份共计21年，占比33.3%。根据对1956—2018年连云港降水长系列的分析，枯水及偏枯年份、平水年份、丰水及偏丰年份基本相当，枯水及偏枯年份略多，因此，连云港降水量基本稳定。

通过线性回归模型和t检验分析，连云港降水量序列的有减小的变化趋势，但不显著；通过小波分析，连云港年降水量存在4年、7年、19年和28年左右的周期，其中第一主周期为28年、第二主周期为19年。