群机器人自组织聚集行为及协同围捕研究
2019-11-07麻轩海
杨 卫,曾 亮,麻轩海
(1.中北大学 电子测试技术国防科技重点实验室,太原 030051; 2.中北大学工作仪器科学与动态测试教育部重点实验室,太原 030051; 3.浙江红旗机械有限公司,浙江 德清 313200)
近年来,随着机器人技术的发展[1],机器人群体协同控制受到越来越多的关注。关于群体模式形成的建模方法主要有基于几何图论法、基于行为的方法、人工物理法等[2-4]。
陈世明等[5-6]在群体空间存在可观测链假设条件下,个体通过计算出包括自身位置在内所有可观测范围内的个体位置所决定的最小外接圆圆心,并将其作为个体的目标位置,最终实现了群体的聚集。Desai[7]提出一种控制图指派算法,将一个有向无环控制图用于约束群体空间位置关系,并给出一个四层的模块化体系结构,实现了群体队形的有效控制。Zhen等[8]对智能体的交互拓扑建模,将每条边与相邻智能体之间的时变权重相关联,并验证该时变拓扑图可以在预定时间范围内完成聚集。采用图论结合控制理论的方法对群机器人系统控制,其优点在于其形式化理论较为成熟,然而却无法胜任含有大量成员的群体分布式控制。
Spears等[9-10]受自然界物体间相互作用规律的启发,提出了基于“人工物理(AP)”的分布式控制方法,通过模拟物理学中的万有引力原理实现了控制群体系统组队的目的。徐望宝等[11-12]提出了一种组群机器人队形控制的人工力矩法,通过引入吸引线段式主——从队形图建立了组群机器人的系统模型,实现了群机器人的队形控制。
基于行为的方法是Brooks[13]在研究细胞机器人行为时提出的一种群体控制结构,该法优势在于并行、分布及实时性,且控制策略的获得相对容易。MarcoDorigo[14]受社会昆虫启发,采用行为法研究实现了近视机器人的聚集,其中个体只能感觉到整个环境中有限的范围,其控制器使用了进化和概率论的方法;Soysal和Sahin[15]为个体机器人制定了的三种简单行为:排斥、接近、静止,通过感知交互并改变系统参数实现了动、静两种状态下的聚集行为。由于基于行为法需要不停的迭代调整个体行为,Brambilla[16]提出一种自顶向下的行为设计方法。这种自顶向下的行为法虽然减少了个体行为的迭代过程,但却增加了设计中系统模型的迭代修正过程,加大了群体设计的复杂度。刘强[17]将基于行为的方法与不同的机器学习方法相融合,应用于机器人编队控制中,解决了常规的基于行为的方法中参数配置困难的问题。张明亮等[18]基于多Agent理论,确定了战时装备维修保障过程中的各类型Agent实体、行为及交互规则,并借助Anylogic仿真平台实现了模型的建模。综述以上方法,本文将人工物理法与自下而上的行为法相结合,进行群机器人自组织行为的建模分析。
1 聚集行为运动控制模型
假设群机器人(Swarm Robots)系统SR={R1,R2,…,RN},N为群体规模,xRi(t)∈R2表示Ri(i=1,2,…,N)在t时刻的位置,vRi(t)∈R2(||vRi(t)||≤vmax)为Ri在t时刻的速度,PRi(t)={||Rj|dij=||xRi(t)-xRj(t)≤r, andRj∈SR}为Ri在t时刻感知范围内机器人集合,其中r为最大感知半径,个体Ri(i=1,2,…,N)在t时刻的感知状态空间表示为:Si(t)={xRi(t),vRi(t),PRi(t)}。
1.1 运动目标的确定
通过感知范围内个体决策与群体决策的加权计算产生目标,个体在t+1时刻的目标通过简单的个体感知中心与感知范围内群体的感知中心来确定,表示为:
(1)
式(1)中: size(PRi(t))为个体感知范围内机器人的数量;λj、λk为个体决策目标的权重。通过权值不同区别自身与其他成员在决策中的作用,实际设计中,为实现个体同构且行为规则简单,λj、λk按照同样的方法进行取值。
1.2 基于质点系力学模型的状态转移方程
将群机器人看作一个质点系力学系统,每个个体都受其目标吸引和其感知范围内其他个体的排斥,在合力作用下,个体不断调整自身的运动状态,找寻动态的平衡。本文依据群机器人聚集的行为要求,从函数的角度采用线性力与指数型力模型对个体之间的行为进行约束。
1) 线性力模型描述力随距离的线性变化关系。
目标对Ri产生的吸引力FA和感知范围内邻居对个体产生的排斥力FR分别为:
(2)
2) 指数型力模型描述力随距离的指数变化关系。
指数型吸引力和排斥力模型分别为:
(3)
个体机器人在运动过程中所受合力构成包含四种方式,如表1所示。
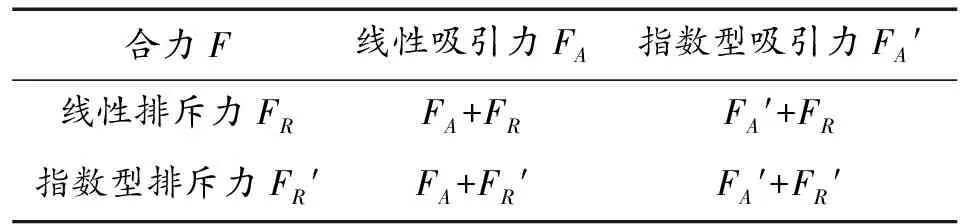
表1 个体合力构成方式
假设所有机器人质量为1,在方程式(2)、式(3)合力作用下,采用牛顿加速度模型a=F/m,可得个体状态转移方程为:
vRi(t+1)=vRi(t)+F
xRi(t+1)=xRi(t)+vRi(t)
(4)
通过此方程可以实现所有机器人位置与速度在空间中的状态转移。
1.3 基于感知状态权值分配的个体状态转移
机器人运动过程中,正前方感知范围内的环境状态对其下一步决策通常起着更大的作用,以下将个体状态转移函数分成方向角函数与速率函数分别加以分析设计。
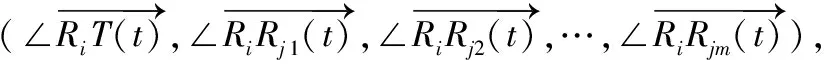
φRi(t+1)=f(x1(t),x2(t),…,xm+1(t))
(5)
(x1(t),x2(t),…,xm+1(t)) =
其中,xi(t)∈[0,2π)表示第i个决策条件,所有决策条件构成机器人t+1时刻的m+1维决策空间,f为决策空间上的线性泛函。
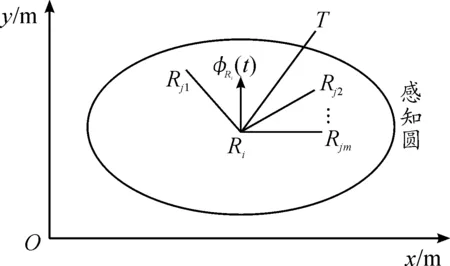
图1 机器人局部感知

(6)
相反情况,驻点具有吸引作用,则可得:
(7)
线性范函综合决策空间中所有因素,通过线性叠加实现机器人下一时刻方向角的选取,其表达式为:
(1) 在抗滑桩间距为最佳桩间距时,桩后土拱与桩侧土拱联合并存,联合的土拱可分解为两个单独的土拱[14]。
(8)
(9)

v(t)=g(y1(t),y2(t),…,ym+1(t))
(10)
式(10)中,yi(t)为m+1维状态中第i项的速率函数,在安全距离外机器人做加速运动,直到最大速度vmax,反之做减速运动,直到停止。安全距离的计算可以根据机器人的牵引力、制动力以及机器人质量求得,在此假设最大加速度为a,则相对t时刻速度yi(t)的安全速度为:
(11)
大于安全速度须做减速运动,小于安全速度可以做加速运动,直到vmax后匀速运动,根据方向角函数设计的原理可得:
(12)
式(12)中,yi(t)∈[0,vmax]。

(13)
2 聚集行为评价指标及实验结果分析
2.1 聚集行为评价指标
为了分析群机器人采用力学模型聚集的性能,定义一些性能指标加以评价。
1) 簇数。聚集过程中,群机器人形成一些相对密集的小群体,称之为簇,表示为cluster,小群体的数量称为簇数,表示为n=size(cluster),并用cluster(j)表示第j簇,nj=size(cluster(j))表示第j簇的个体数量。簇数反映了群机器人系统的整体聚集程度或分散程度,簇数越多,群体聚集效果越差。
levelAggre越大聚集度越高。
3) 簇内分布均匀度。对于群内每一个机器人Ri,找出其最近的邻居并记录其距离值序列dmin_Ri(i= 1,2,…,N),用序列的方差表示分布均匀度,即:
levelUniformity越小,则分布均匀度越高。
2.2 聚集行为实验分析
在50×50平面区域内随机布撒机器人,通过个体目标确定和个体状态转移模型进行聚集行为实验,研究不同情况下的聚集效果。实验中设置:vmax=4 m/s,αi=1,σ=0.8, Δt=0.2 s,a=1 m/s2,个体与其目标之间的不受力距离设为dRT=0,吸引力系数为ω1=γ1=0.5,个体与个体之间的临界距离设为dRR=2,排斥力系数为ω2=γ2=0.2。
群体规模由10~50个递增,个体感知半径r由10~30递增,分别对质点系力学模型、感知状态权值分配模型进行仿真实验,得到了关于不同模型的群机器人聚集行为模式,以下是对聚集行为的分析。
2.2.1影响簇数的因素
在50×50平面区域内随机布撒机器人,由上文仿真实验可知:当机器人规模超过20,感知半径大于20时,簇数基本为1,能实现全体聚集。本文针对机器人规模为50,感知半径分别为10、20、30三种情况下,分别进行10次实验,得到簇数随感知半径变化的统计结果如图2所示,可知感知半径是影响聚集性能的重要因素。

图2 簇数随感知半径变化的统计结果
2.2.2聚集度试验结果分析
图3为对不同感知半径、不同群体规模情况下群体聚集度试验统计结果,统计结果表明聚集能力最强的是感知状态加权模型,另外,还可以发现聚集度较强的模型受感知半径、群体规模的影响较大,而聚集度最弱的模型几乎不受感知半径、群体规模的影响,这为我们后面设计群机器人区域覆盖提供了依据。
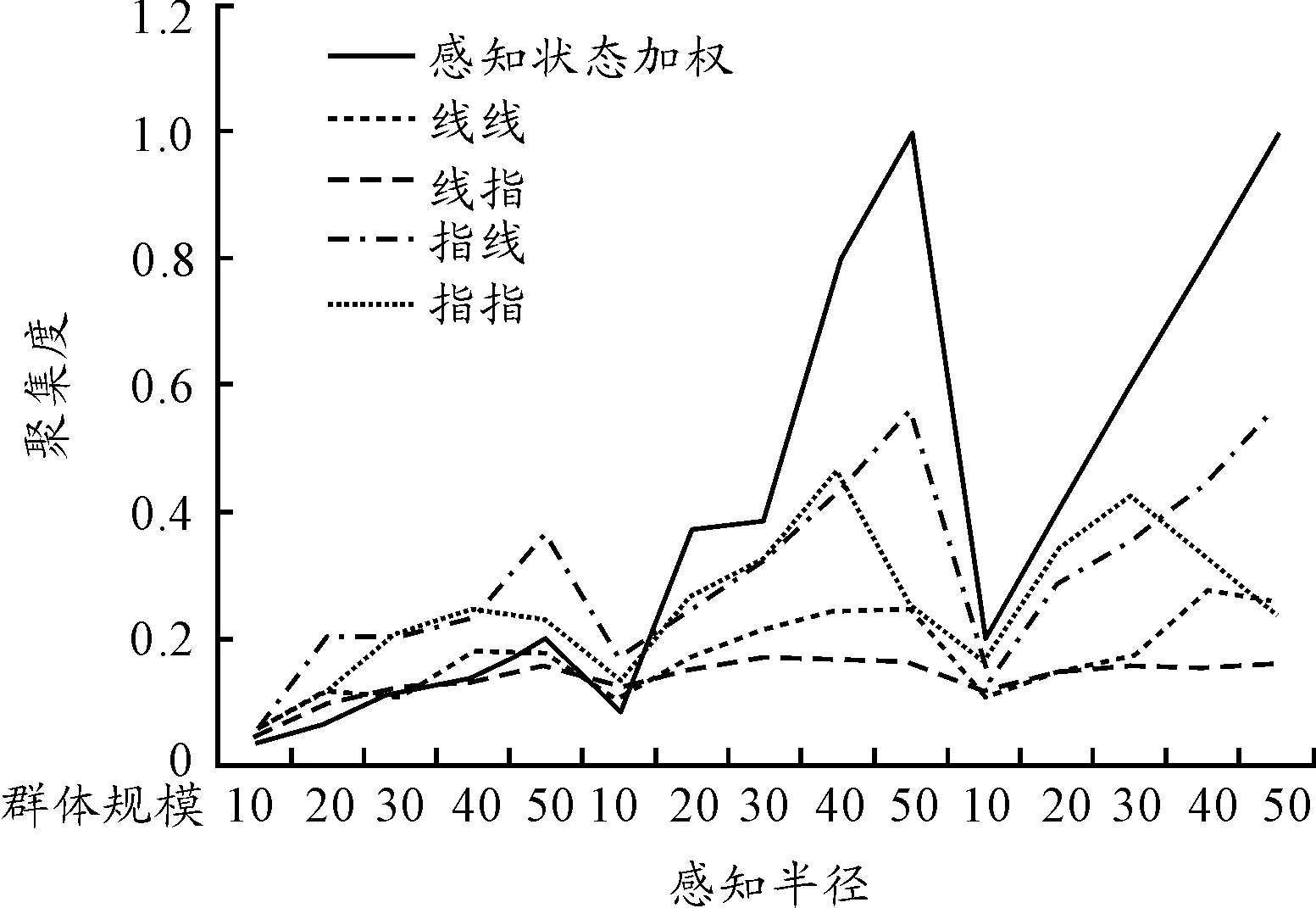
图3 不同模型的聚集度
2.2.3簇内分布均匀度试验结果分析
图4为对不同感知半径、不同群体规模情况下群体均匀度实验统计结果。结果显示不同模型在感知半径大于20时均匀度相对稳定,特别关注线指模型,其均匀度表现最优,其均匀度非常稳定。
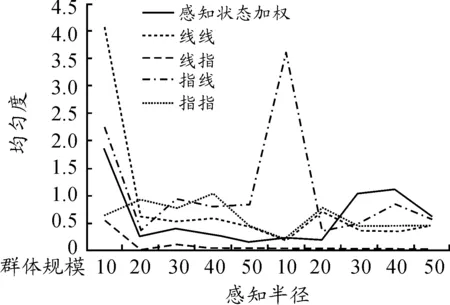
图4 不同模型的均匀度
另外,关于线指模型均匀度,作者进行了更加深入的研究,当其运行处于稳定状态时,簇内聚集度只与个体之间的临界距离、作用力系数相关,而与个体其他参数无关。
3 模型验证试验
选用均匀度特性极强的线指模型,通过个体临界距离的设置产生群机器人领域行为,以实现群体对目标的围捕为目的进行仿真实验。
当有目标出现时,首先发现目标的机器人受目标吸引作用向目标靠近,同时通过广播解除群机器人系统领域行为模式,启用围捕模式,个体之间充分协作,可以相互靠近,在聚集行为模型中,缩小个体之间最小临界距离,通过目标引导的群机器人聚集行为实现围捕。
在区域100×100范围内随机布局群机器人,规模N=10、30,个体感知半径r=20,个体之间临界距离dij=2。
目标作直线运动时:起点为[0,0],速率为1 m/s,方向角为π/4;
目标作曲线运动时:起点为[0,0],速率为1 m/s,方向角为π/4+sin(t/5),采用线性吸引指数型排斥模型,围捕结果如图5所示。

图5 线性吸引指数型排斥模型群体围捕结果
实际测试中,由于场地限制,选用30 m×30 m的平坦地面进行试验,设置目标起点(0,0),速度1 m/s,方向角函数t/100,以曲线运动掠过布撒区域,检测线性吸引指数型排斥模型对目标的围捕效果。得到了如图6所示的实验结果,其中标识target处为目标系统规划出的针对目标的最优围捕点。

图6 围捕实验结果
4 结论
本文通过对群机器人自组织聚集行为进行建模,并对不同运动控制模型进行分析比较,为进行机器人群编队实现不同功能时选用最优运动模型奠定了基础。进一步通过对机器人群对目标的协同围捕仿真试验,验证了建立的线性吸引力、指数排斥力模型聚集度与均匀度好的特性。
