天基对地动能武器的打击范围研究
2019-11-07刘庆国刘新学杜林峰洪大银
刘庆国,刘新学,武 健,杜林峰,洪大银
(1.火箭军工程大学研究生院, 西安 710025; 2. 96901部队,北京 100094;3. 78102部队, 成都 610036)
争夺制天权已经成为各军事大国在作战中的首要任务之一[1],天基对地动能武器作为一种战略进攻型武器,可以实现从太空对地面高价值目标进行打击的能力,具有较强的战略威慑力。打击范围的研究可以为后续判断天基对地武器是否具备对某一目标具备打击能力打下一定基础。典型SGKW的转移轨道分为两部分,过渡段和再入段,采用零攻角弹道式再入方式[2]。
现有研究SGKW的文献主要包括该类型武器及其应用的阐述[3],天基对地武器的转移轨道优化[4-5]。文献[6]研究了组合动力天基对地飞行器轨的覆盖范围,文献[7-8]研究了惯性系下SGKW的最大横程与打击范围,但研究均未考虑地球自转和地球的扁率。目前来说,SGKW的研究仍然存在一些不足。
本文在现有研究基础上考虑了地球自转,地球扁率和地球引力摄动因素,更加准确的描述了SGKW的数学模型;确定目标是否处于SGKW的打击范围内的方法为判断目标的经度纬度坐标是否处于SGKW打击的经度纬度范围内,现有研究的文献并没有直接的研究。综合以上两个问题,本文在给出了地固坐标系下天基对地动能武器的运动微分方程后,建立了有限推力作用下天基对地航天器转移轨道的优化模型,在此基础上建立了以经度纬度为坐标的天基对地航天器落点范围的求解模型并进行了仿真计算。
1 SGKW在地固坐标系中的运动微分方程
本文在描述SGKW机动变轨和再入大气层运动状态的运动微分方程组中考虑了地球自转角速度ωe和地球引力位函数的J2项,同时地球半径r为随纬度变化的变量(图1为典型SGKW的转移轨道示意图)。
(1)
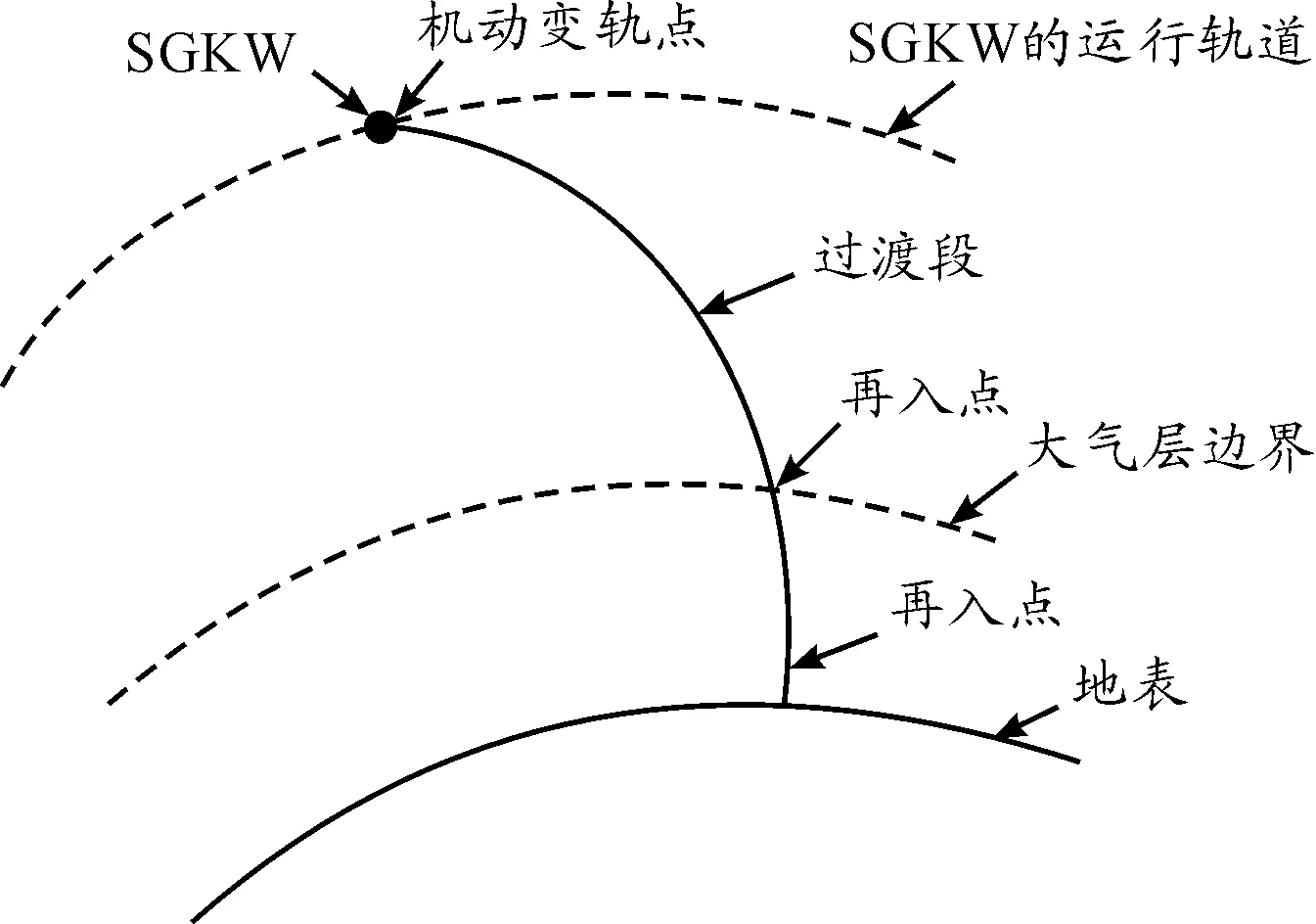
图1 SGKW转移轨道示意图
无量纲化参数的计算公式:
(2)
式(2)中rref,mref,Vref,tref和gref的表达式为
(3)
式(3)中:μ(μ的值为6.67e-11 N·m2/kg )为引力常数,m0为航天器的初始质量。r为地球半径,其公式为
r=a[0.998 320 047+0.001 683 494cos(2Φ)-
0.000 003 549cos(4Φ)+0.000 000 008cos(6Φ)]
(4)
描述SGKW在太空中的运行轨道,一般采用采用经典的轨道6根数(半长轴a,偏心率e,轨道倾角i,升交点赤经Ω,近地点幅角Ω,真近点角f)。轨道六根数与绝对坐标系中运动参数速度VI,速度倾角γI,航向角ΨΙ,地心距rI,经度ΘI,纬度ΦΙ为关系和绝对坐标系中运动参数与地固坐标系下参数的关系分别如式(5)和式(6):

(5)
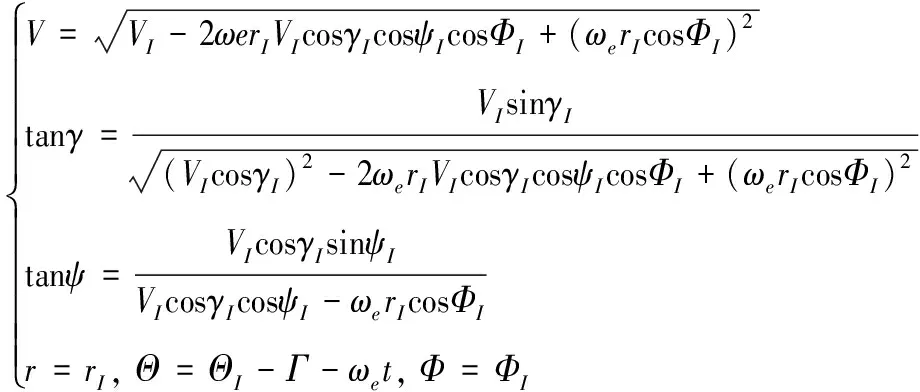
(6)
2 SGKW打击范围的求解模型
本文打击范围的求解是在经度和纬度为坐标下进行的。研究思路为:
a) 求解落点距离机动变轨点最小经度或纬度;
b) 求解落点距离机动变轨点最大经度或纬度;
c) 取a)和b)最小和最大的经度或纬度之间的若干点,并求解所取点对应的边界点;
d) 连接a)、b)和c)求解的点即可求得SGKW的打击范围。
在求解落点距离机动变轨点最小经度或纬度,落点距离机动变轨点最大经度或纬度,和最小和最大的经度或纬度之间的边界点时均需要对转移轨道进行优化求解。本文采用混合法求解转移轨道的研究思路为:以a)、b)和c)对应的落点为优化指标,利用Pontryagin极小值原理将轨道优化问题转换为两点边值问题,利用GA对协态变量初值和部分参数进行优化搜索,得到转移轨道和打击范围。
对于研究思路中a)、b)和c)对应的优化问题,其优化指标不同,分别为

(7)

(8)

(9)
J1、J2和J3分别对应研究思路中a)、b)和c)的优化指标。Θm和Φm分别机动变轨点的星下点的经度和纬度;Θb和Φb分别为落点的经度和纬度。
根据Pontryagin极小值原理,引入Hamiltonian函数:
(10)
依据式(10)可以推导得到协态变量满足微分方程组(仅考虑过渡段):

(11)
(12)
(13)
依据式(13)和极小值的充分条件可得到最优推力方向如式(14)所示:
(14)
式(14)中sgn( )为符号函数。

(15)
计算优化指标J1和J2时,横截条件为
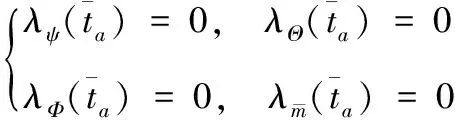
(16)
计算优化指标J3时落点满足位置约束:

(17)
故相应的横截条件分别由式(18a)和式(18b)所示:
当0≤i≤45° or 135°≤i≤180° 时;

(18a)
当 45° (18b) 由性能指标和状态约束可知: (19) 步骤2适应度函数值如式(7)、式(8)和式(9)所示。给定染色体后,依据式(11)积分并满足式(15)~式(19)的约束。计算种群个体的适应度函数值及群体的适应度函数值总和。 步骤3利用RWS方法进行选择,然后进行交叉、变异产生下一代种群。 步骤4重复执行步骤2和步骤3,直到算法收敛(ε=10-6)或者达到最大迭代步数。 通过上述计算,即可求得给定变轨时刻下时间最短的转移轨道。 假设SGKW的总质量m为1 000 kg,携带燃料400 kg,发动机推力T为105 N,燃气喷气速度Ve为2.5 km/s。其运行轨道参数为:半长轴a为6 750 km,偏心率为0.001 5,轨道倾角为 41°,升交点赤经为 95°,近地点幅角为 105°,真近点角为0。以SGKW运行到纬度 -39.001°,经度 -59.525° 机动变轨为例进行仿真计算,以机动变轨时刻为0时刻。 轨道倾角大于45°,按照打击范围求解模型中大于45°的优化指标进行解算。表1和表2给出了距离机动变轨点最小经度处各变量优化结果和落点参数,表3和表4给出了距离机动变轨点最大经度处各变量优化结果和落点参数,图2给出了SGKW的打击范围。通过图2可以看出:打击范围基本保持在SGKW运行的星下点轨迹的两侧。仿真计算表明本文提出的方法能够实现SGKW打击范围的求解(表1、表2、表3和表4中Va和Vb的单位为km/h,γa、Φb和Θb的单位为°,ta和tb的单位为s)。 表1 距离机动变轨点最小经度处各变量优化结果 表2 距离机动变轨点最小经度处落点参数优化结果 表3 距离机动变轨点最大经度处各变量优化结果 表4 距离机动变轨点最大经度处落点参数优化结果 图2 SGKW的打击范围 在考虑了地球自转,地球扁率和地球引力摄动条件下,提出了以大地经纬度为坐标的SGKW的打击范围求解模型。仿真结果表明了模型的可行性,本文的研究成果丰富了空间作战的相关理论并可直接作为仿真模块应用于相关系统软件中。在未来研究中,快速求解打击范围将是一项重要研究方向。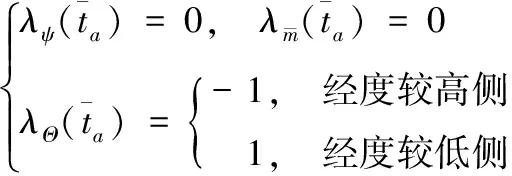


3 仿真计算及结果分析





4 结束语
