基于“列维扩展”信号子空间的双基地MIMO雷达相干角度估计

郑志东，董 莉，文 刚，徐 凯

(1.北方电子设备研究所，北京 100191；2.国防科技大学电子对抗学院，安徽 合肥 230037；3.西藏军区参谋部信息保障处，西藏 拉萨 850100；4.解放军77526部队，西藏 拉萨 850100)

0 引言

双基地MIMO雷达[1-2]是MIMO技术与双基地雷达相结合而形成的一种新型体制雷达，它不仅继承了传统双基地雷达在抗干扰、反侦察、反隐身等方面的优点，而且具备虚拟阵列孔径扩展、提高目标检测和参数估计性能、降低双基地雷达“三大”同步要求等诸多优势，因此引起了国内外学者的广泛关注。

双基地MIMO雷达能够通过接收端的信号处理，同时估计出目标相对于发射阵列的角度(发射角，Direction of Departure，DOD)和目标相对于接收阵列的角度信息(接收角，Direction of Arrival，DOA)，从而实现对目标的定位。因此，收发角度估计算法是双基地MIMO雷达实现目标定位的一个关键技术。目前，众多学者在双基地MIMO雷达提高参数估计精度[3-4]、高效快速估计[5-6]、复杂环境背景下[7-8]参数估计等方面进行了大量研究。但大多以假设目标为不相干或者不相关为前提，而且并未考虑到由于双基地MIMO雷达孔径扩展而造成运算复杂度增大的问题(尤其在M和N阵元数较大时)。当目标之间存在相干性时，上述算法的估计性能将急剧下降，甚至失效。因此，本文考虑相干目标间双基地MIMO雷达的快速收发角度估计问题。

对于相干目标，要实现正确解相干获得准确收发角度估计的关键在于有效恢复接收信号协方差矩阵的“秩”。空间平滑方法[9]是一种常用且有效的解相干处理方式，通过对数据的平滑构造列满秩协方差矩阵。文献[10—11]分别利用接收数据进行Hankel矩阵、Toeplitze矩阵重构，从而得到秩满阵，其本质上和空间平滑算法相类似。空间平滑算法虽然能够有效进行目标解相干，但是都存在着不同程度的阵元孔径损失，其算法的估计性能还有改善的空间，而且需要利用多次快拍数据来逼近理论统计值，算法所需的计算量较大。根据双基地MIMO雷达回波信号的特点，通过构造“列维扩展”信号子空间来降低由接收协方差维数增加而增大的计算量，证明在相干目标条件下，该“扩展”信号子空间仍为列满秩阵，并针对“扩展”信号子空间的特点，提取出与“扩展”域目标角度相对应的旋转不变因子，进而估计出目标的收发角度。最后利用空域滤波法实现了目标的配对。

1 信号模型及“扩展”信号子空间构造

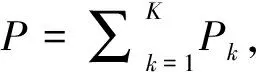
图1 双基地MIMO雷达发射和接收配置图Fig.1 Transmitter and receiver configuration of bistatic MIMO radar

由文献[10]可知，在接收端对第q(q=1,…,Q)个发射脉冲的回波进行匹配滤波，则输出可写为：

yq=K(φ,θ)gq+wq

(1)

由式(1)可得回波信号的协方差矩阵为：

(2)

式(2)中，E为无噪时的协方差矩阵。当不存在多径时，等效目标源个数P即为独立目标源个数K，此时矩阵R的秩rank(R)等于总目标数P，对其进行特征值分解能够得到准确的信号子空间与噪声子空间；而多径情况下P>K，即只有K个独立目标源，这便导致R的秩小于P，秩的降低使得对R进行特征值分解时噪声与信号子空间不能完全分离，从而无法利用子空间类算法估计角度。因此，在角度估计之前应构造一个秩为P的解相干矩阵，并利用该矩阵恢复准确的信号子空间。以下利用E中的元素来构造解相干矩阵。

将MN×1的接收矢量排列成N×M的数据矩阵Xq，则有

Xq=A(θ)ΛqBT(φ)+Wq

(3)

式(3)中，A(θ)为N×P的接收方向矢量，B(φ)为M×P的发射方向矢量，Λq=diag(gq)，Wq为噪声wq的重排项。由式(3)可求得如下协方差矩阵Rr和Rt：

(4)

(5)

进一步，由式(4)、式(5)可构造出矩阵Rtr：

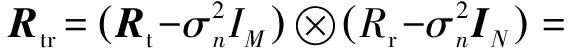
(6)

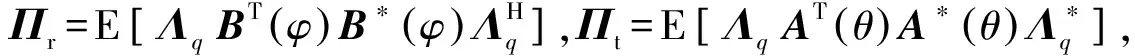
证明：分两种情况进行论述。

1) 当仅有单快拍数据时(Q=1)，由于rank[B(φ)]=P，且Λq为对角元素非零的对角阵，因此有rank[ΛqBT(φ)]=P，进一步，利用矩阵秩的性质[13]rank(AAH)=rank(A)可得，rank(Πr)=rank{ΛqBT(φ)[ΛqBT(φ)]H}=P。同理可得rank(Πt)=P，rank(Πtr)=P2。

2) 当存在多快拍数据时，由矩阵Hadamard积的性质，可以将矩阵Πr变换为：

(7)

2 角度估计算法

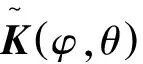
(8)

令Ust1和Ust2分别为Us的前N(M-1)行和后N(M-1)行组成的子矩阵，则类似于ESPRIT算法的旋转不变因子提取，由Ust1和Ust2可提取出与φ相关的旋转不变因子矩阵，即

(9)

(10)

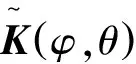
(11)

(12)

(13)

(14)

(15)

由上述分析可知，整个算法的计算步骤为：

1) 利用接收数据计算协方差矩阵Rr和Rt，即式(4)和式(5)；

2) 对Rr和Rt进行特征值分解，取出P个大特征值对应的特征向量up和vp，并计算“扩展”信号子空间Us；

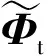
以下分析“列维扩展”信号子空间算法(Extended Signal Subspace)的计算量(以下简称为ESS方法)，并与空间平滑算法以及基于块Hankel矩阵方法[10](Block Hankel-based，BHB方法)的计算量进行比较。为了便于比较，假设双基地MIMO雷达的发射和接收阵元数目均为奇数，且分别为M=2M′+1和N=2N′+1，在利用空间平滑算法时，取子阵阵元数为M′和N′，则发射和接收所形成的子阵个数为M′+2和N′+2，因此需要计算(M′+2)(N′+2)个M′N′×M′N′维的协方差矩阵。在利用BHB方法时，以参数估计最优来选择块Hankel矩阵的行列参数，即取I=M′,J=N′。由上述分析可知，ESS方法的计算量主要集中于：1) 协方差矩阵的估计及其特征值分解，所需的计算量为O{QMN(M+N)+M3+N3}；2) 求解子矩阵Ust1和Usr1的伪逆，并对式(9)和(11)进行特征分解，所需的计算量为O{2[N(M-1)P4+M(N-1)P4]+P6}；3)进行收发角度配对，所需的计算量为：O{(P-1)N2M+(P+2)(P-1)NM2/2}。由此可知，本文的总计算量约为：O{QMN(M+N)+M3+N3+2P4[N(M-1)+M(N-1)]+P6+(M2N+MN2)(P-1)}；而二维空间平滑算法的计算量为：O{(M′+2)(N′+2)Q(M′N′)2+(M′N′)3+grgt(M′N′+1)(M′N′-P)}，其中gr,gt分别为沿DOA和DOD方向搜索的网格数；BHB算法的计算量为：O{QM2N2+M3N3+2P2[(M′-1)N′+(N′-1)M′]+P3}。由于快拍数Q以及网格数gr,gt远大于M,N,P，因此易得ESS算法的计算量小于BHB以及空间平滑算法的计算量。图2给出了二维空间平滑，块Hankel矩阵构造法以及“扩展”信号子空间法的运算量与快拍数之间的变化关系，其中取M=7，N=7，P=4，M′=3，N′=3，gr=gt=500。

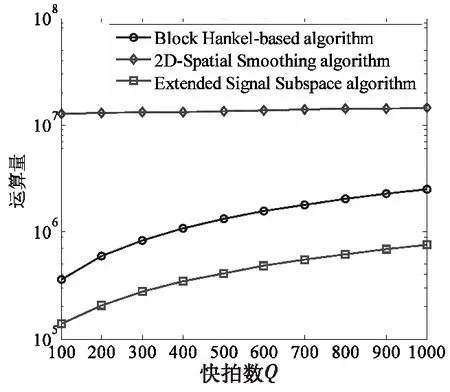
图2 三种算法的运算量比较Fig.2 Comparison of the computational complexity of the three algorithms

3 实验仿真和数据分析

实验1 角度估计算法的有效性。考虑收发阵元数目M=N=7，空中存有3个相干目标，位置分别为(φ1,θ1)=(-15°,-30°)，(φ2,θ2)=(0°,0°)，(φ3,θ3)=(15°,30°)，SNR=5 dB，分别进行两组实验：1) 快拍数Q=1；2) 快拍数Q=100。图3(a)、(b)分别为Q=1时扩展信号子空间法和块Hankel矩阵构造法的目标位置估计结果。图4 (a)、(b)分别为Q=100时两种算法的目标位置估计星座图。

图3 单快拍数下两种算法的目标位置估计星座图Fig.3 The target localization results of the two algorithm with single snapshot

图4 快拍数Q=100时两种算法的目标位置估计结果Fig.4 The target localization results of the two algorithm with Q=100

实验2 相干目标下不同算法的估计精度比较。实验条件同实验1。分别比较“扩展”信号子空间算法、空间平滑算法以及块Hankel矩阵算法的估计性能。空间平滑时分别取m0=n0={4,5,6}三种情况进行实验。利用块Hankel矩阵算法时取行列参数I=J=4。图5 (a)和(b)分别为目标DOA和DOD的RMSE随SNR的变化曲线，实验时取Q=50，且在每个SNR下独立进行200次Monte-carlo实验。

分析图5(a)和(b)可知，在快拍数Q=50情况下，“扩展”信号子空间算法的估计性能优于块Hankel矩阵算法以及不同子阵数下的空间平滑算法。这主要是由于：由块Hankel矩阵算法和空间平滑算法都是属于阵列平滑类算法，它们均以牺牲一定的阵元孔径来实现解相干，存在着不同程度的性能损失；而“扩展”子空间算法通过对Rtr的构造实现解相干处理，并没有阵元孔径损失。因此，“扩展”子空间算法的估计性能优于其它两种角度估计算法。就本实验而言，“扩展”子空间算法利用了MN=49的阵列孔径，而块Hankel矩阵算法仅利用了IJ=16的阵列孔径。

图5 相干目标角度的RMSE随SNR的变化曲线Fig.5 The change curve of RMSE versus SNR for coherent target angles

实验3 非相干目标下不同算法的估计性能比较。显然，“扩展”信号子空间算法不仅适用于相干目标，而且对于非相干目标同样适用。本实验将该算法与ESPRIT算法进行比较。考虑收发阵元数M=N=10，空中存有3个不相关目标，位置分别为(φ1,θ1)=(-10°,-20°)，(φ2,θ2)=(0°,5°)，(φ3,θ3)=(15°,-10°)，图6 (a)和(b)分别为目标收发角的RMSE随SNR的变化曲线，图中还给出目标角度CRB的性能曲线。实验时取Q=10和Q=50两种情况，且在每个SNR下独立进行200次Monte-carlo实验。图7给出了目标角度的RMSE随快拍数Q的变化曲线，实验时取SNR=0 dB。

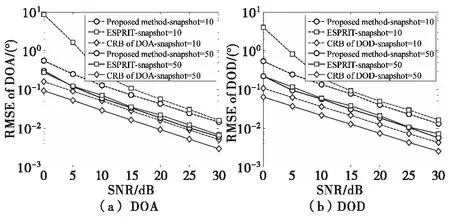
图6 非相干目标角度的RMSE随SNR的变化曲线Fig.6 The change curve of RMSE versus SNR for non-coherent target angles

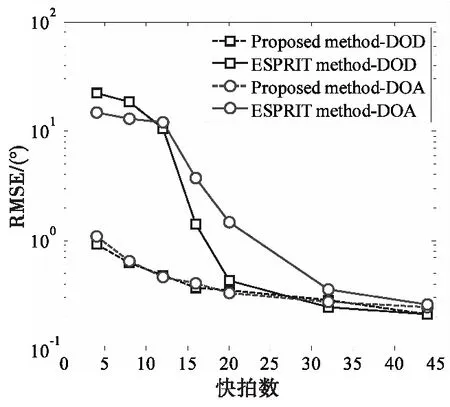
图7 目标角度的RMSE随快拍数的变化曲线Fig.7 The change curve of RMSE versus snapshot for target angles

分析图6 (a)和(b)可知，在Q=10时，本文算法的估计精度优于ESPRIT算法，尤其在SNR较低情况下，优势更为明显；在Q=50时，本文算法的估计性能与ESPRIT算法相接近，同时，在高SNR时，两种算法的估计精度都趋近于目标的CRB值。由图7 可知，在快拍数小于20时，ESPRIT算法的估计性能差于本文算法，随着Q的增大，两者的估计性能趋于一致。从两种算法的信号子空间构造来看，ESPRIT算法需要估计出MN×MN维的协方差矩阵，而本文算法仅需分别估计出M×M和N×N的协方差矩阵，在利用时间平均代替统计平均时，估计较大维数(ESPRIT算法)协方差矩阵所需的快拍数应大于估计较小维数(本文算法)协方差所需的快拍数目。因此，在快拍数较小时，文本算法能够获得较为准确的协方差矩阵估计值。

4 结论

本文针对此问题，提出了基于“列维扩展”信号子空间的双基地MIMO雷达相干角度估计方法。实验表明，“列维扩展”信号子空间算法能够对单快拍接收数据进行有效的角度估计，且不存在阵列孔径损失，其估计精度优于块Hankel矩阵构造法以及空间平滑算法。本文算法同样适用于非相干目标，当快拍数据较少时，本文算法的估计精度优于ESPRIT算法，尤其在信噪比较低情况下，估计性能的优越性更为明显。因此，本文算法更适用于实际中快拍数据较少的情况下。