某超B级高度剪力墙结构动力弹塑性分析
2019-11-06郭天祥郑智辉
郭天祥 郑智辉
(厦门上城建筑设计有限公司 福建厦门 361012)
0 引言
钢筋混凝土剪力墙结构整体性好,抗侧刚度大,但是其基本周期短,地震惯性力较大。超B级高度剪力墙结构高度超过规范限值较多,计算要求和构造措施均应比规范规定更严格。另外,《高层建筑混凝土结构技术规程》[1]第5.1.13条规定,B级高度的高层建筑结构,宜采用弹塑性静力或动力分析方法补充计算。
本文以厦门泰禾·首玺B2#楼为例,介绍超高层剪力墙结构的动力弹塑性分析。动力弹塑性分析是将地震波输入,由结构初始状态开始,求解每一步地震响应,并逐步积分直至地震作用结束的方法,据此结果用以考察结构在大震作用下的抗震性能是否满足性能目标。
1 工程概况
泰禾海沧项目位于厦门海沧区,其中B2#楼建筑平面尺寸为35.0×21.3m,房屋高度172.9m(共59层),其中上部14层为复式,层高除首层5.35m外均为2.9m,场地内设两层地下室。主要平面及立剖面如图1~图3所示。
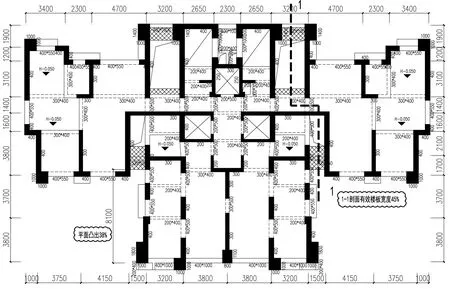
图1 结构标准层平面图
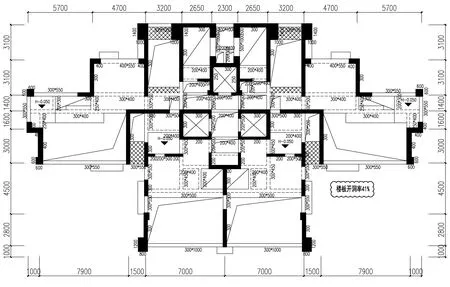
图2 复式上层结构平面图

图3 立面及剖面图
该工程设计使用年限50年,设防烈度为7度(0.15g),地震分组第二组。基本风压为0.8kN/m2,地面粗糙度类别为B类。
2 弹性设计分析
该工程为住宅项目,结构平面宽度较小,且隔墙较多,因此采用钢筋混凝土剪力墙结构。高度超限、楼板不连续、平面不规则等超限情况,建筑高度超B级,高度超限是该项目的主要问题。
2.1 结构体系设计与布置
主要竖向构件布置:顶部14层为复式户型,标准层局部柱墙到复式楼层后取消。底层墙体500mm厚,与复式楼层相关Y向墙体1~9层为400mm厚,9层以上变为300mm厚,其余Y向墙体1~9层为400mm~300mm厚,9层以上为300mm~200mm厚。X主要墙厚为300mm厚,局部楼梯间外墙为400mm厚,到上部减为300mm厚;主要剪力墙端柱为1000mm×1400mm,并在底部加强区加设型钢。
梁系布置:外圈梁主要为550mm高,局部外圈梁(南侧平面凸出部分)为1000mm高;主要的连梁及框架梁高度为500mm。
2.2 结构分析的主要设计结果
根据工程超限情况及超限论证会专家意见,结构性能目标如表1所示。另外,底部加强部位以上轴压比大于0.25的剪力墙墙肢还应设置约束边缘构件,中震小偏心受拉的墙肢按特一级构造,并根据拉应力情况设置型钢。

表1 结构关键部位及其性能目标
弹性计算分析,主要采用YJK计算分析,并并辅以MIDAS/Building对分析结果进行校核。
小震CQC弹性分析主要计算结果表明,YJK和Building软件计算结果比较吻合,层间位移角、自振周期、最小剪重比等各项结构总体指标均能满足规范要求。各构件根据相应性能目标要求,按中震计算结果进行承载力设计。
3 大震动力弹塑性分析
在大震作用下,结构内力重新分布,从材料本身到整体性能均表现出非线性行为。因此,该工程采用Building建立三维结构整体模型,材料采用非线性的本构关系,进行罕遇地震作用下动力弹塑性分析,并以此考察其抗震性能。
3.1 主要技术参数指标
3.1.1模型考虑的非线性因素
在该工程的弹塑性分析过程中,考虑了以下非线性因素[2]:①材料非线性:钢筋、混凝土及钢材的弹塑性特性均采用材料非线性本构关系模拟,以此来表现构件的弹塑性发生、发展直到破坏的全过程;②几何非线性:在结构变形后的几何状态上建立结构平衡方程,计算过程中考虑“P-Δ”效应带来的影响。
3.1.2材料本构关系
非线性分析模型与弹性分析的模型相同,其中,对结构材料进行弹塑性本构关系的定义。
(1)基于材料的本构模型
软件中混凝土本构关系,采用《混凝土结构设计规范》[3]附录C中的单轴受压应力-应变本构模型,钢筋采用双折线的本构模型,屈服前后刚度不同,屈服后刚度使用折减后刚度。
混凝土剪切本构采用了理想弹塑性双折线模型,屈服前后的刚度不同,如图4所示。

(a)理想弹塑性剪切 (b)修正武田三折线滞回模型图4 本构模型
(2)基于截面的塑性铰滞回模型
该工程钢筋混凝土和型钢混凝土构件,采用如图4所示的修正武田三折线模型,三折线铰输出两种状态,一是开裂和开裂到屈服前状态,二是屈服和屈服后状态。
(3)非线性墙单元
剪力墙采用基于纤维模型的非线性剪力墙单元进行模拟。该类墙由多个墙单元构成,每个墙单元水平向和竖向被分割成一定数量的纤维,每根纤维都有一个积分点。
剪切变形计算时,综合每个墙单元的4个高斯点位置的剪切变形。墙单元的剪切“应变等级”的定义为:墙单元剪切本构关系中单元的实际剪切应变与屈服剪应变的比值(γ/γ1)。
钢筋的材料本构中,钢筋的“应变等级”定义为:钢筋实际应变与屈服应变比值(ε/ε0)。
图中用不同颜色区分,具体如图5所示。
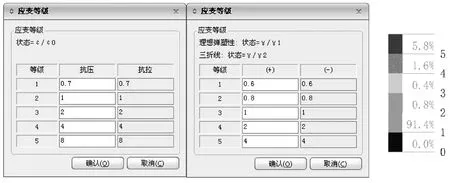
图5 钢筋(左)及剪力墙(右)的应变等级
3.1.3地震波的选取及输入
该项目采用两组天然波和一组人工波,与之作对比的是规范中的加速度反应谱,并按规范把场地特征周期加上0.05s。参照《建筑抗震设计规范》5.1.2条及条文说明的选波要求,3条地震波为:
Superstition Hills-02_NO_719,Tg(0.51);
Superstition Hills-02_NO_724,Tg(0.52);
ArtWave-RH2TG045,Tg(0.45)。
时程分析分两步进行,一是施加重力荷载代表值,二是施加地震作用,输入地震波时,峰值取310cm/s2。模型一共需输入3组地震波记录进行计算,每组地震波分别选取结构X、Y向作为主、次方向分别计算,主、次方向输入地震峰值加速度按1∶0.85进行调整。结构阻尼比取0.05。
3.2 动力弹塑性分析结果
结构抗震性能评价,通过对结构整体性能(底部剪力和结构变形)和构件性能(材料损伤)两个方面来考察。
3.2.1结构底部剪力
3条地震波在大震作用下的底部剪力约为小震作用下的3~5倍,其中,天然波2(时长18.8s)基底剪力最大。下述讨论均以此条地震波Y向的结果举例进行分析。
3.2.2结构变形
结构在地震作用主方向Y向的最大层间位移角分别为1/163、1/148、1/172,计算结果均小于规范规定的1/120限值,如图6所示。
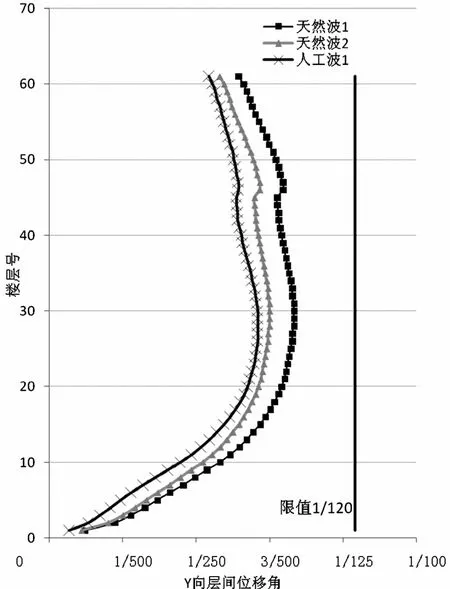
图6 最大层间位移角
3.2.3材料损伤
本小节从构件的塑性变形与变形限值的关系来对结构进行评估,以此保证结构不因局部构件破坏而产生严重的破坏或倒塌。
3.2.3.1剪力墙受剪
Building中剪切破坏判断标准,采用基于抗剪极限承载力的名义屈服应变方法:
首先,计算剪力墙构件极限抗剪承载力,此时使用的是材料强度标准值;然后,采用剪力除以墙体有效截面来计算名义屈服剪应力;最后,γ1=τ1/G,也就是屈服剪应变=屈服剪应力/剪切模量,其中G=0.4E。
Building程序设定γ1=0.00022,以此作为判断混凝土受剪破坏的临界点。有研究资料表明,γ1应为0.0 004~0.0 005。γ1分别取0.00 022及0.0 004进行计算表明,两个模型层间位移角相差很小,但是剪力墙剪切破坏的结果却变化很大,如图7所示。因此,后续论述中,主要针对地震作用过程中剪力墙的破坏顺序及程度,从概念上对计算薄弱部位采取加强措施。

(γ1=0.0002)(γ1=0.0004)图7 不同屈服剪应变墙铰状态对比
为进一步了解B2#楼剪力墙在罕遇地震作用下的塑性发展情况,选取图8所示3片剪力墙(7轴、8轴、X向)进行观察,具体如下:
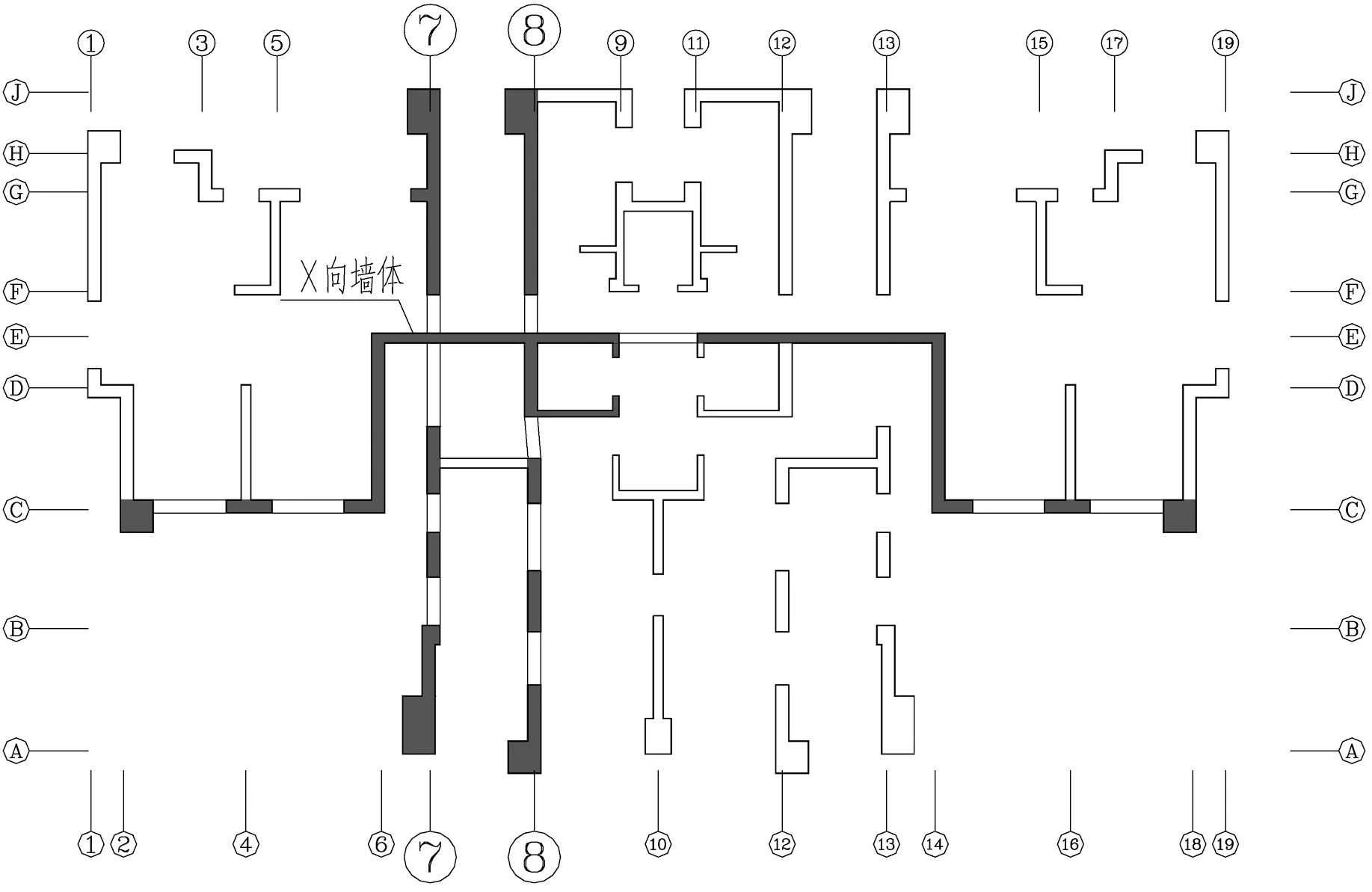
图8 B2#楼平面示意图
图9所见,6.5s时7轴处剪力墙在8~16层连梁开始出现损伤,此时大部分剪力墙尚未屈服,但是竖向构件收进下层(即42~45层)位置出现塑性发展;13.5s时,J轴位置8~19层开始出现塑性损伤,竖向构件收进的下层剪力墙塑性持续发展,B轴~C轴间连梁及短肢墙塑性发展情况严重;到18.5s时,地震波加载结束,G轴~J轴位置在9~38层塑性发展情况严重,B轴~C轴间短肢墙及连梁的塑性应变等级在几乎全高的范围均发展至5级[4]。

(t=6.5s) (t=13.5s) (t=18.5s)图9 7轴剪力墙混凝土剪切塑性发展过程

(t=4.5s) (t=13.5s) (t=18.5s)图10 8轴剪力墙混凝土剪切塑性发展过程

(t=4.5s) (t=13.5s) (t=18.5s)图11 X向剪力墙混凝土剪切塑性发展过程

图12 部分楼层剪力墙混凝土剪切塑性发展过程注:左图为第1、7层(型钢变化层),右图为第45、46层(复式收进层)
图10~图11分别为8轴级X向剪力墙混凝土剪切塑性发展过程,具体情况如图中所示。
另外,由图12可以看出,底部加强部位(1~6层)外圈端柱设置型钢,有效地提高了剪力墙在大震作用下的抗震能力;竖向构件收进楼层的外圈端柱,同样有必要增设型钢。
综合分析以上塑性发展过程可以发现:
(1)剪力墙受剪损伤首先发生在短肢墙及连梁位置,该位置计算配筋也较大;Y向墙肢两端设置端柱,计算配筋也较大,需设置型钢以满足承载力计算要求。
(2)在竖向构件收进部位的剪力墙受损情况比较严重,后续结构设计中应采取加强措施。
(3)X向底部墙体较Y向墙体破坏严重,主要原因有:结构Y向由风荷载控制,剪力墙布置较多,剪力均匀承担;X向由地震作用控制剪力墙较少且集中,E轴处连续墙长7.6m,刚度较大;Y向墙体多已布置型钢混凝土端柱,X向墙体未考虑性能化设计。
鉴于前述计算结果,总体而言,竖向构件的损伤较严重的位置主要位于以下3处:(1)刚度较大的位置。Y向长墙抗侧刚度大,两侧容易出现因偏拉引起的抗剪能力削弱。(2)短肢剪力墙位置。墙肢截面较小,地震剪力作用下截面抗剪难以满足要求。(3)竖向构件收进的位置。该位置刚度突变、受力复杂,且竖向压重小,抗剪难以保证。
针对剪力墙损坏较明显的部位,采取对应的加强措施后重新进行动力弹塑性分析。主要措施有:E轴处7.6m长X向剪力墙中间开洞,适当削弱刚度;提高竖向构件收进上下楼层抗震等级及配筋率;提高底部加强区竖向构件抗震等级至特一级,提高墙身竖向配筋率,并按中震正截面不屈服、斜截面弹性进行配筋;提高下部楼层短肢墙及过渡层剪力墙配筋率。
加强措施及计算结果如图13~图15所示。加强措施主要为:对配筋的调整,对整体计算结果影响不大。短肢墙、底部加强部位剪力墙及竖向构件收进部位等的损伤情况均得到有效改善。
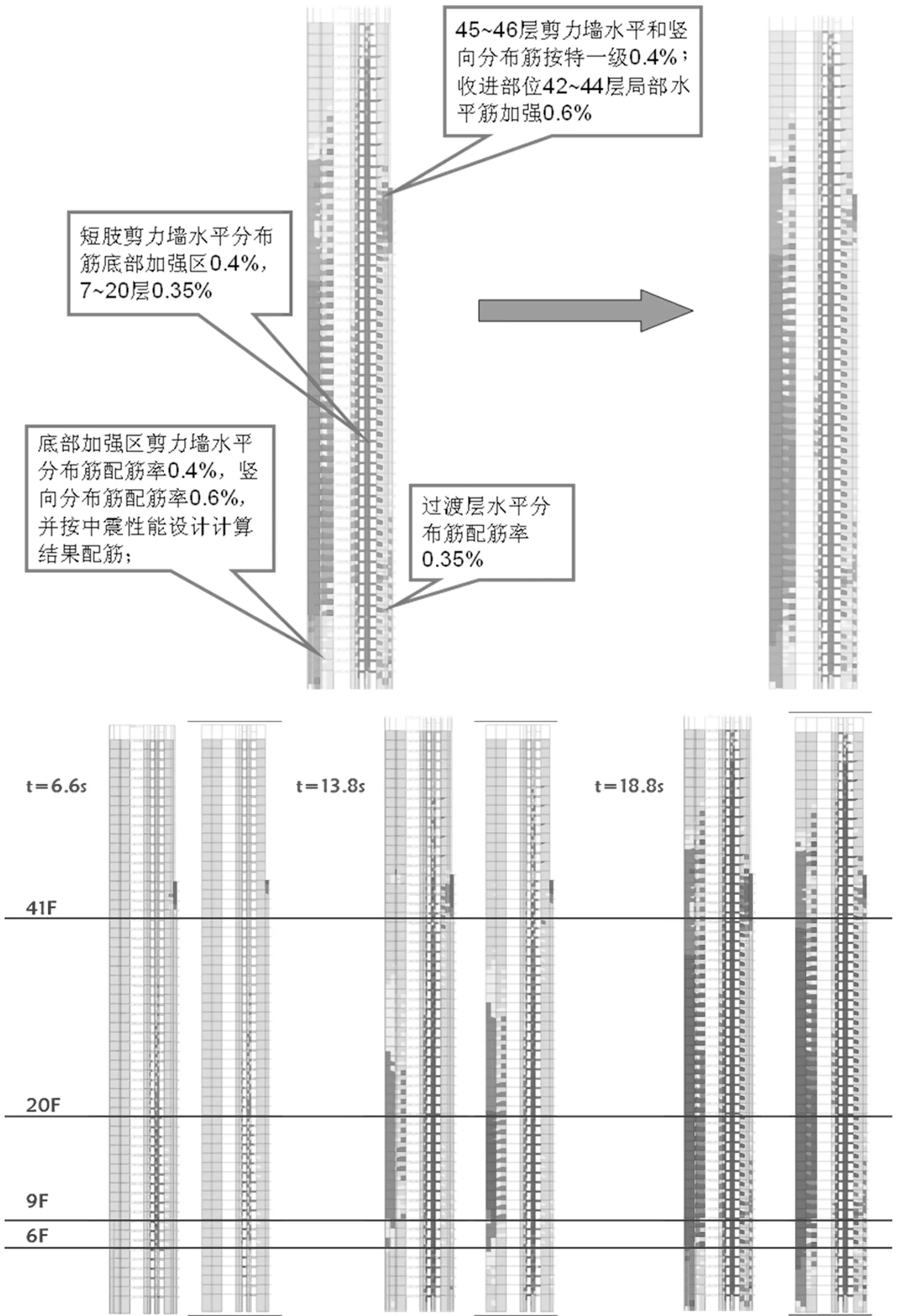
图13 7轴剪力墙采取加强措施前(左图)后(右图)结果对比

图14 8轴剪力墙采取加强措施前(左图)后(右图)结果对比

图15 X向剪力墙采取加强措施前(左图)后(右图)结果对比
鉴于软件计算参数取值对剪力墙损伤结果影响较大,为防止构件发生脆性受剪破坏,该工程控制剪力墙截面在大震下受剪满足截面控制条件,即按《高层建筑混凝土结构技术规程》式3.11.3-4进行验算。
验算结果表明,剪力墙截面均满足上述要求,部分墙肢的剪压比验算结果如表2所示。
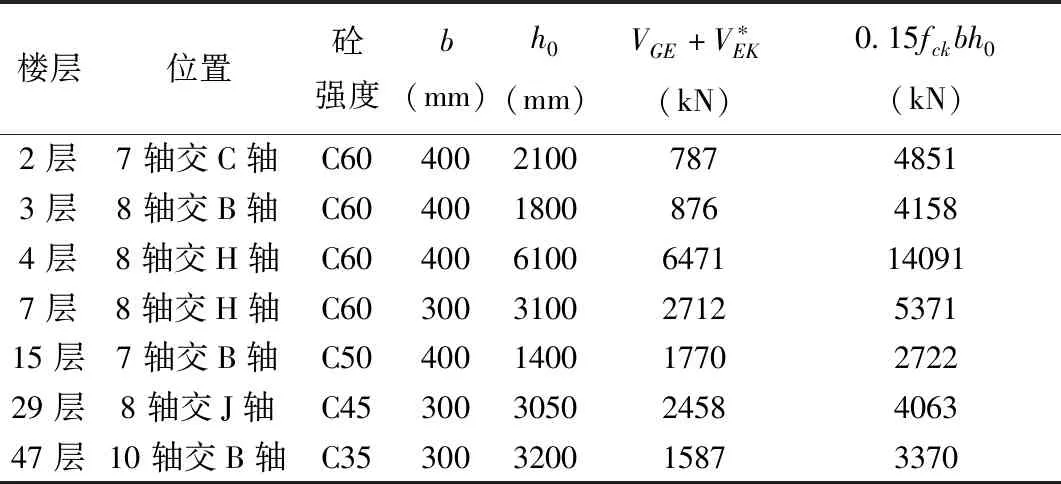
表2 墙肢剪压比验算
3.2.3.2剪力墙钢筋受拉
设计对剪力墙的目标要求如下:关键构件→轻度损坏,普通竖向构件→部分构件中度损坏。参考文献[5]一书中的表7-4:剪力墙损伤性能评价对应量化标准,钢筋方面性能水平轻度损坏及中度损坏具体参考标准如下:轻度损坏:钢筋塑性应变,γp=1~3;中度损坏:钢筋塑性应变,γp=3~6(γp表示钢筋塑性应变与屈服应变的比值)。
图16为钢筋应变等级。

图16 钢筋应变等级
从图16中可以看出,钢筋应变等级绝大部分处于1级~2级之间,即γp=0.7~1,因此剪力墙在大震下满足性能目标要求。
4 结论
计算结果表明,目前采用的结构体系能满足“大震不倒”的抗震性能目标。结构弹塑性发展历程及抗震性能总结如下:
(1)输入3组罕遇地震波进行弹塑性时程分析后可知,结构层间位移角满足规范最低要求(1/120)且有余量。
(2)罕遇地震波持续作用下,整体结构的弹塑性发展历程表现为:剪力墙连梁最先出现塑性铰,随着地震作用的进行,连梁塑性变形逐步加大,累积耗能。
(3)短肢墙及竖向构件收进的下层部位,塑性发展情况严重,后续结构设计中应采取加强措施。
(4)底部加强部位主要抗侧力墙肢端柱采用设置型钢的钢骨混凝土柱,这些端柱对剪力墙能有效提高其强度、刚度以及延性性能。从计算结果上看,对剪力墙在大震作用下的抗弯、抗拉剪承载力起到明显的有利作用。
该工程属于超限超高层建筑,结构计算结果均满足现行规范和规程的要求。设计时在充分计算的基础上,采取了合理的结构布置,根据计算结果及性能化设计,对结构的薄弱部位采取有效的加强措施,并采用钢骨混凝土构件加强剪力墙的抗弯、抗拉剪承载力,使得结构具有良好的抗震性能。
